降低多用户大规模MIMO-OFDM系统PAPR的加速近端梯度算法*

华 磊,王亚军,刘 爽

(江苏科技大学 海洋学院,江苏 镇江 212100)

0 引 言

大规模正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)与多输入多输出(Multiple-Input Multiple-Output,MIMO)技术相结合可以发挥两者的优势,实现更快的通信速率和更高的频谱利用率,MIMO-OFDM已经成为下一代无线通信中的核心技术[1-2]。

但OFDM作为一种多载波技术,当各载波频谱相同或相近时容易导致信号的包络起伏较大,进而造成信号的峰值平均功率比(Peak-to-Average Power Ratio,PAPR)较高。高峰均比信号通常需要带有较大反馈的功率放大器,这就增加了模数转换器和数模转换器的复杂性,同时对发射机内放大器的线性也提出了很高的要求,由此可能导致信号畸变,使信号的频谱发生变化,导致系统的性能严重恶化[3-4]。而将多用户大规模MIMO(Multi-user Massive MIMO,MUM-MIMO)技术应用到工程实际时,必须要求基站使用低功耗的射频链路和功率高效的射频功率放大器[5],这就需要发射信号具有较低的PAPR。为满足使用高效的功率放大器和降低多用户间的干扰这两个要求,迫切需要使用更加有效的方法来降低系统的PAPR。

目前降低OFDM系统PAPR的方法有很多[6-9],尽管可以应用于点对点的MIMO-OFDM系统,但由于大规模MIMO系统中接收端用户协同工作极为困难,因此运用到大规模MIMO-OFDM系统中显得不甚合理。在文献[10]中,作者给出了基于快速递推截断算法(Fast Iterative Truncation Algorithm,FITRA)的低PAPR非线性预编码设计。其设计方法联合考虑了MUM-MIMO预编码、OFDM调制和PAPR减小,核心思想是通过利用无穷范数代替PAPR,从而得到满足无穷范数约束下的最小化多用户间干扰(Multi-user Interference,MUI)问题。文献[11]中,作者提出了一种添加干扰信号降低系统PAPR的方法,并利用交替方向乘子算法(Alternative Direction Method of Multipliers,ADMM)对其进行求解。在该方法中,作者在预编码后的频域信号中加入一个干扰信号,同时对该干扰信号做出限制,保证其位于每个子载波所对应的信道响应矩阵的零空间中,因此该方法在获得好的PAPR性能同时,不会为整个系统带来额外的信号失真和带外辐射。文献[12]中,作者通过最速梯度下降方法来解决多用户预编码和降低PAPR联合的问题,利用MIMO信道矩阵的高维零空间来降低信号的PAPR,但其方法得到的误符号率(Symbol Error Rate,SER)性能较差。上述方法都能够获得好的PAPR抑制性能,但均存在着算法计算复杂度高的缺陷。

针对以上问题,本文利用加速近端梯度算法(Accelerated Proximal Gradient Method,APGM)来设计降低多用户大规模MIMO-OFDM系统中发射信号PAPR的低复杂度快速收敛算法,该算法在抑制发射信号的PAPR同时也能获得好的SER性能。

1 多用户大规模MIMO-OFDM系统模型

在如图1所示的多用户大规模MIMO-OFDM系统的下行链路中,假定基站配置有M根发射天线,同时服务于K个单天线移动用户,且满足K≪M。在本文中,假定信道状态信息在发射端完美已知。OFDM载波数目为N,将载波分为数据载波Γ和自由载波Γc两部分,其中数据载波用来传输数据,而自由载波不传输任何数据,放于频带的两端用作保护间隔。向量sn∈CK×1为在第n个子载波上传输的包含K个终端用户的数据,对于数据载波n∈Γ时,sn选自某个调制星座字符集;对于自由载波n∈Γc时,有sn=0K×1。为消除接收端多用户间的干扰,需对用户信息符号进行线性预编码:wn=Gnsn,其中,wn∈CM×1为预编码后的信号,Gn∈CM×K为相对于第n个子载波的预编码矩阵。常用的预编码方案有匹配滤波(Matched Filtering,MF)、迫零(Zero-forcing,ZF)和最小均方误差预编码等。对于发射机已知信道矩阵Hn∈CK×M,则迫零预编码矩阵可以写为,接着将归一化的频域信号wn,∀n重新排序后分配到各个发射天线上[x1,x2,…,xM]=T[w1,w2,…,wN],T表示图1中重新排序的映射。其中,向量xm∈CN×1表示第m根天线上的频域信号。然后对频域信号xm,∀m进行离散傅里叶逆变换(Inverse Discrete Fourier Transform,IDFT)得到相应的时域信号ym,m∈1,2,…,M。完成并行到串行转换之后,通过对每根天线上的时域信号ym,∀m添加循环前缀来避免码间干扰。最后将这些时域样本转换成模拟信号,通过射频链路传输到无线信道中。

图1 大规模MIMO-OFDM系统框图

2 峰值平均功率比

OFDM信号由多个独立的调制信号叠加而成,能够有效地对抗频率选择性衰落,对于第m根天线上的频域信号xm∈CN×1,相应的时域连续信号可以写为

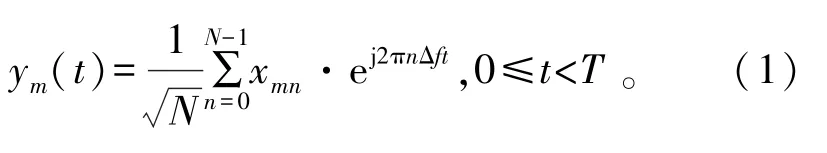
式中:T为OFDM符号时间;Δf为子载波频率间隔;N为子载波数。由于各个子载波的相位相互独立,相互叠加后的OFDM信号就会有非常大的动态范围。通常使用PAPR来衡量发射信号的波动。PAPR表示信号功率的峰值与均值之比,即

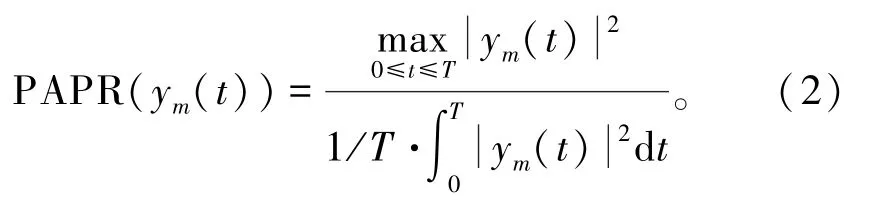
在实际系统中,通常只有发射信号ym(t)的一些离散时间样本,为了更好地近似连续时间信号的PAPR,在获得离散时间样本时采用J=4倍过采样,即

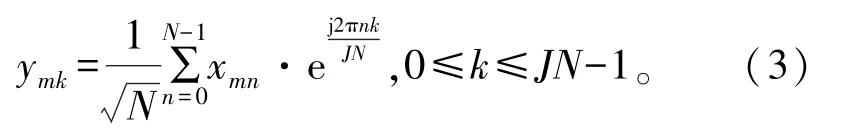
过采样操作也可以表示为ym=FHxm,m=1,2,…,M,其中,FH∈CJN×N表示JN点傅里叶变换矩阵的前N列,J为过采样因子。因此具有J倍过采样的时域样本的PAPR由下式给出:

使用互补累积分布函数(Complementary Cumulative Distribution Function,CCDF)来衡量信号的峰均比,定义为发射信号的峰均比超过门限值的概率,具体表示为CCDF(γ)=Pr{PAPR＞γ},其中γ表示指定的门限值。

3 算法设计

3.1 加速近端梯度算法

加速近端梯度算法用于求解以下形式的问题:

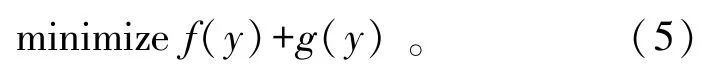
其中:f:Rn→R是连续可微的凸函数;g:Rn→R∪{+∞}为连续的凸函数。算法基本迭代过程如下:

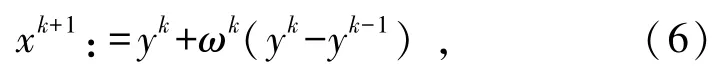
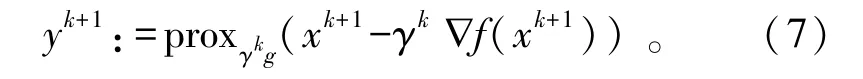
式中:ωk∈[0,1)是外推参数;γk是步长因子,通常选取ωk=k/(k+3)。函 数g(y)的近端算子proxγg(·)定义式如下:

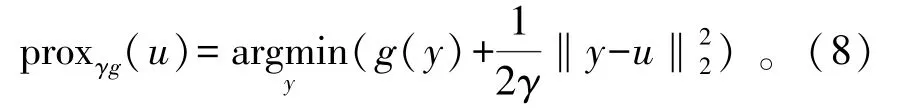
当函数f对应的最小Lipschitz常数为L时,使用固定步长γk=γ∈(0,1/L],该算法以ο(1/k2)的速率收敛于目标值。

3.2 低复杂度APGM算法设计

由于发射天线数量远多于终端用户数量,即M≫K,将会有无限多的预编码信号w≜[wH1,wH2,…,wHN]H满足预编码约束,只需找到一组频域信号wn,n∈1,2,…,N,使其对应的时域信号具有较小的PAPR,同时能够消除多用户间干扰:

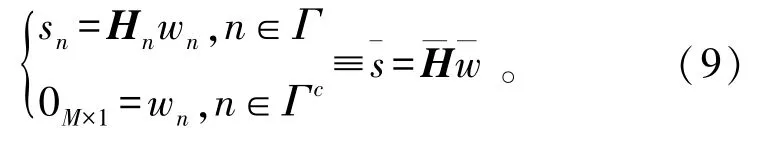
式中:∈C(K×|Γ|+M×|Γc|)×1是所有用户数据符号和自由载波上的0M×1的集合;为块对角矩阵,其主对角块为Hn,∀n∈Γ和IM,∀n∈Γc。为了表述方便,将上述将信号重排序到天线上的过程写为更紧凑的形式,其中。根据系统模型,预编码后的频域信号与原始数据及时域发射信号之间的关系可以用下式表示:

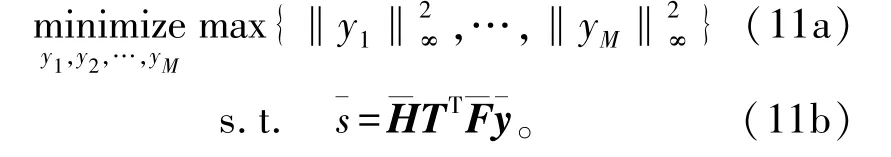
为了简化表示,写成更紧凑的形式:

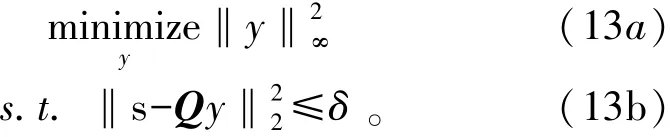
将式(13)转化为可以利用APGM算法求解的形式。将式(13)的放松模型用拉格朗日形式表述为

式中:α是正则化参数。使用APGM来求解问题(14),通常需要计算函数f(y)=‖s-Qy‖22梯度∇f(y)的Lipschitz常数,再根据Lipschitz常数来估计步长γk。梯度∇f(y)的最小Lipschitz常数对应于L=2σmax(QQH),σmax表示为矩阵的最大奇异值。但是计算函数Lipschitz常数复杂度太高,不利于实际工程中的应用。可以用一个线性搜索方法[13]来确定步长γk。利用式(8),函数g(y)=α‖y‖2∞的近端算子可以写成以下形式:

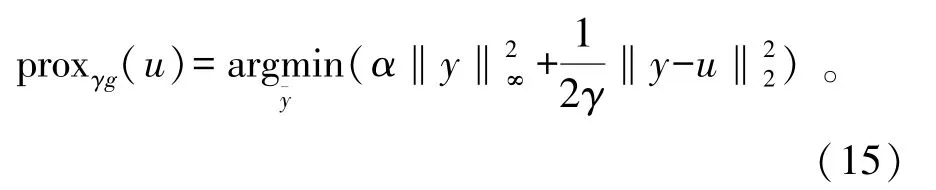
式中:u=xk+1-γ∇f(xk+1)。近端算子(15)可以通过对文献[14]中的方法改进来精确获得(算法1),具体的计算步骤如下:

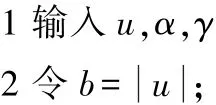
3 对向量b按降序进行排序,s=sort(b,‘descending’)

4 fori=1,2,…,JNM

5 令di=∑i k=1sπ(k),其中sπ(k)表示在向量s中第k大的元素;

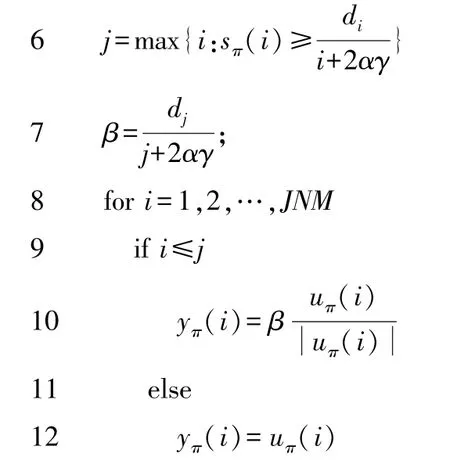
13 end if

14 end for

15 end for

16 returny

以上就是计算ℓ2∞近端算子的过程。根据公式(6)和(7)分别更新变量xk+1和yk+1,求解模型(14)的APGM算法(算法2)如下:

1 输入xk,γk-1,β,其中β∈(0,1)

2 令γ=γk-1

3 fork=1,2,…,K

4z=proxγg(xk-γ∇f(xk))

5 iff(z)≤^fγ(z,xk),where^fγ(z,w)=f(w)+

6 break

7 end if

8 更新γ=βγ

9 end for

10输出yk+1=z

3.3 算法复杂度分析

APGM求解问题(14)由算法1和算法2组成。在算法1中,计算向量b的值需要O(MJN)的复杂度,对向量b进行排序需O(1/2·MJNlb(JN))的计算量,计算j和μ的复杂度为O(MJN)。‖z-y‖22需要计算向量间的乘法运算,其复杂度为O(MJN)。由函数f(y)带来的梯度∇f(y)=QH(Qy-s)计算复杂度为O(K|Γ|M+1/2·MJNlb(JN))。因此,求解(14)的APGM算法的计算复杂度主要来自近端算子的排序和函数梯度的计算,总复杂度为O(K|Γ|M+MJNlb(JN))。APGM算法与其他算法的算法复杂度对比如表1所示,可以看出所提出的APGM复杂度远低于其他方法,同时算法运行时间也远小于其他算法。将各种算法运用在大规模天线阵列中,天线数目的增加随之带来更高的能量消耗,而APGM具有较低的运算复杂度及更快的运行时间,能够很好地在实际系统中应用。

表1 算法复杂度分析

4 仿真分析

将APGM算法与现有的迫零预编码(Zero-Forcing(ZF)Precoding) 方法、匹配滤波预编码(Matched Filtering(MF) Precoding)方法、PMP方法[10]、PRO-ADMM方法[11]、MU-PP-GDm方法[12]进行比较,各种方法的最大迭代次数如表1所示。为验证APGM的有效性,在大规模MIMO-OFDM系统下行链路中进行实验仿真。在基站处设计100根天线,同时为10个单天线用户提供服务。在OFDM系统中,使用IEEE 802.11n中指定的40 MHz模型,子载波个数设为128,其中Γ=108个子载波用于数据传输,在仿真中忽略用作导频的子载波;Γc=20个子载波用于频带保护,使用互补累积分布函数来评估PAPR降低性能。采用具有格雷映射的16QAM调制方式,信道为频率选择性信道,在时域具有多抽头结构,且抽头数设为D=8。信道时域响应矩阵{Hd,d=1,2,…,D}的元素服从均值为0,方差为1的复高斯分布,对应的频域响应矩阵为

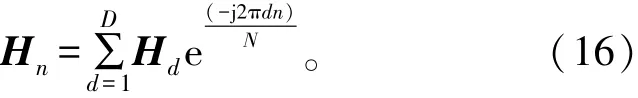
图2给出了APGM与ZF算法、MF算法、PMP方法、PRO-ADMM算法、MU-PP-GDm方法对PAPR抑制的性能比较。在CCDF=Pr(PAPR＞γ)=10-3时,APGM算法只需30次迭代就可将PAPR降低到2 dB,比ZF方法降低了10 dB以上,比PMP方法的PAPR值小1 dB,比MU-PP-GDm算法的PAPR值小3.2 dB,还比PRO-ADMM算法的PAPR值少3.9 dB;PMP算法可以将PAPR降到3 dB,MU-PP-GDm算法可以将发射信号的PAPR降低到5.2 dB,PROADMM算法将信号的PAPR降低到5.9 dB。APGM只需30次的迭代就可以达到这样效果,而PMP方法需进行约2 000次的迭代才能将PAPR值降到2.7 dB。从图中可以看到,APGM的PAPR减少性能优于PMP、PRO-ADMM、MU-PP-GDm等算法。

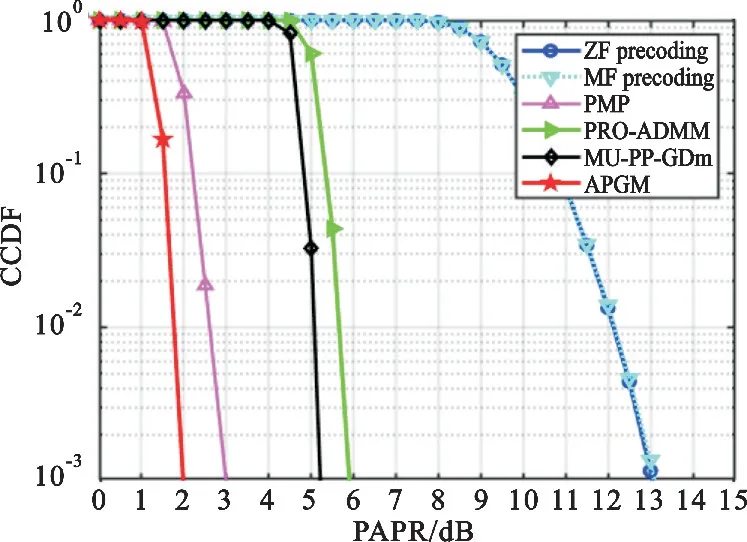
图2 不同优化算法的PAPR值比较

图3比较了不同算法在加性高斯白噪声信道上的SER性能,其中信噪比(Sigal-to-Nise Ratio,SNR)定义为SNR=E{‖ym‖}/N0,其中N0表示接收器的噪声方差。可以看到与ZF方案相比(在SER=10-2时),APGM的信噪比仅比理想值多1.3 dB左右,与PMP方法相比少0.7 dB,比PROADMM算法少2.5 dB,与MF方法相比少3.8 dB,同时还比MU-PP-GDm算法少6 dB以上。

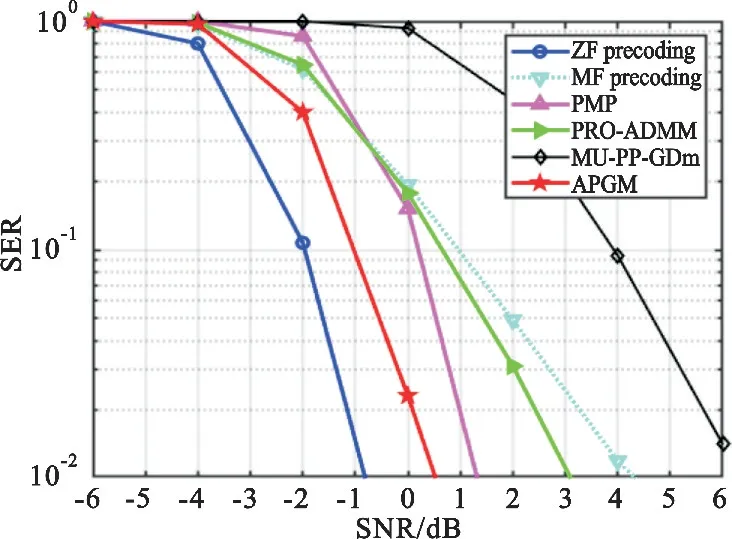
图3 不同优化算法的SER性能分析

图4给出了不同算法的迭代次数对应的PAPR对比。CCDF=Pr(PAPR＞γ)=10-3时设计的APGM经过10次迭代就可以将PAPR降低到3.8 dB,经过20次迭代PAPR降低到2.4 dB,而经过30次迭代PAPR值可以降到2 dB,比迫零预编码方法PAPR值减少了10 dB以上;PRO-ADMM方法外迭代200次、内迭代2次,总共需400次迭代才能将PAPR值降到5.9 dB;MU-PP-GDm方法经过50次迭代可以将PAPR值降到5.2 dB;而PMP方法在100次迭代后PAPR值仅降到10 dB,PMP方法2 000次迭代后PAPR值降到2.7 dB。

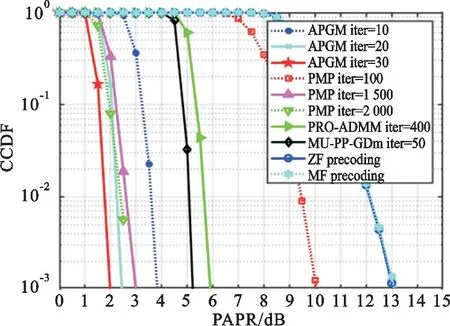
图4 不同迭代次数的PAPR值比较

在SER=10-2时,从图5中可以看到APGM在经过20次迭代之后信噪比值为0.2 dB,与ZF方案相比损失1 dB,30次迭代之后得到的信噪比为0.5 dB。而PMP方法在1 500次迭代后信噪比为1.2 dB,与ZF方法相比损失2 dB,PMP方法经过2 000次迭代之后得到的SNR为1.3 dB。PROADMM方法内外循环迭代共400次之后获得的信噪比为3 dB,MU-PP-GDm算法经过50次迭代得到的信噪为7 dB。从以上仿真实验可以看出APGM具有更低的复杂度和更快的收敛速度,只需少量的迭代就可以获得更低的SER和更好的PAPR抑制效果,因此APGM比存在的其他方法更高效,更利于工程实际中的应用。

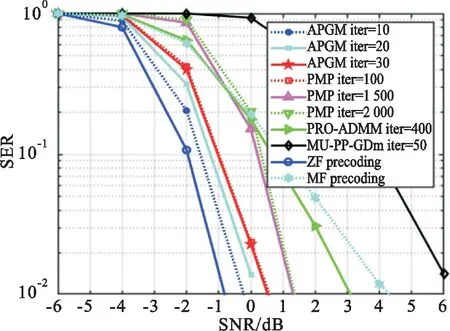
图5 不同迭代次数的SER值比较

5 结束语

本文针对大规模MIMO-OFDM系统中较高的PAPR值问题提出了一种低复杂度的APGM,核心是利用发射天线的额外自由度将MU预编码、OFDM调制和PAPR抑制联合成凸优化问题。仿真结果表明,APGM只需很少的迭代次数就可以降低发送信号的PAPR,获得好的SER性能,同时具有更低的计算复杂度,更适合工程实际中的应用。在今后研究中,考虑将APGM用于非完美信道状态信息下的系统模型,同时将发射信号的功率及带外散射作为模型的约束,以进一步增强系统的稳健性。