一种地下排水管道流速测量方法*
张文鑫,许 荆
(北京信息科技大学 自动化学院,北京 100192)
0 引 言
目前,我国城市地下排水系统运行普遍不尽人意,经常发生污水通过雨水系统流入河道或者雨天管道排水不顺导致道路积水等现象[1],给城市环境带来严重的影响,同时影响市民正常生活。发生上述这些现象主要是因为早期地下管道设计不合理、雨、污水管道混接、管道系统不完善、管道淤积、管道堵塞等造成管道排水能力下降等原因。由于地下管道处于封闭密封环境,具有一定腐蚀性且伴随着有毒气体,再加上图纸档案缺失,因此通过人力巡检对地下管网的检修和维护缺乏科学的依据。
随着科学技术的发展,涌现出一些新的管道监测技术,如质量式流量计、容积式流量计、压差式流量计、叶轮式流量计、超声波流量计、电磁流量计等。但这些流量计或者流速计在地下管道监测工程项目中均存在不同的缺陷,无法完全满足现场使用要求。测量精度相对较高的ADCP设备无法进入地下管道测量,接触式流速测量设备由于收到管道中污渍和漂浮物的影响,需要人员定期检修和维护,需要耗费大量的人力,因此针对地下管网流速测量最好的方式是采用非接触、低功耗、维护方便的流速测量设备。
目前非接触式雷达流速仪被广泛用于河道流速监测,采用Ku频段[2],河道测流要求的测量动态范围大(0.3~20 m/s),速度分布与边界存在一定关系[3]。由于其载频小,理论上可以通过降低采样率提高采样点来降低误差,但该方法会增加雷达工作时长。在实际工程项目中,需要覆盖较大的动态范围,采样率不能太低,同时采样点数直接关系到处理器运算量,也不能太大,因此调整参数提高测速精度的效果是有限的。针对测速误差大的问题,一些学者提出超分辨率算法来提高测速精度,如Rife-Jane法[4]、能量重心法[5]、频谱细化算法[6]等,但复杂的算法增加了运算量,导致功耗的增加,同时由于液体表面流速成分接近容易出现相邻干扰。管道流速范围一般小于2 m/s,通常在0.6~0.8 m/s,当水流量小时流速小于0.3 m/s,多普勒频率小,水流表面纹波较小,雷达有效反射面积(Radar Cross Section,RCS)小,且雷达中频高通滤波放大电路引入一定测速盲区,Ku频段雷达流速仪难以测量0.3 m/s以下流速场景。
太赫兹雷达由于具有载频高、带宽大等优点,被广泛用于无线通信[7]、近距离成像[8]、空气测量[9]、医学应用[10]等,相比于传统的管道监测技术,本文提出的太赫兹雷达流速监测设备具有体积小、功耗低、非接触、精度高等优点[11],非常适合用于地下管道流速监测应用。
1 雷达测速原理
如图1所示,雷达安装固定于管道上方俯仰向下,天线与流速方向呈30°~50°夹角。雷达发射固定频率的连续波电磁信号,电磁波信号达到流体表面时发生布拉格散射,同时叠加流体多普勒频移,雷达接收机接收散射回波信号,利用本振信号和回波信号进行混频提取多普勒中频信号。

图1 雷达测速原理图
雷达发射电磁波信号可以表示为
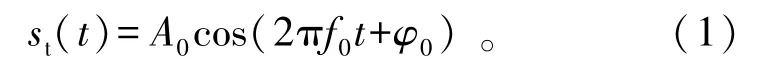
式中:f0为电磁波载波频率,本文采用的是0.12 THz作为雷达的载波;φ0为发射信号初始相位。电磁波信号到达速度为v的流体表面后反射信号可以表示为
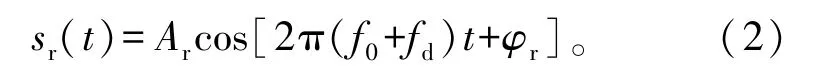
将接收信号式(2)和发射信号式(1)进行混频提取得到中频(Intermediate Frequency,IF)信号:

雷达中频放大电路需要经过隔直或者高通滤波器滤除直流信号和低频包络信号,导致测速存在一定盲区。当安装角度和流速一致时,多普勒频率与发射电磁波载频成正比,选择更高频率载频可以获取的频率更大中频信号输出,对于相同的高通滤波电路,测速盲区更小。
综上,可以得到流体表面流速的计算结果为

式(4)中,载频、光速、倾角为已知固定值,只需要计算多普勒频率即可计算流速。
2 雷达硬件系统设计
为了实现雷达系统的小型化和低功耗,同时保证高精度,本方案雷达系统采用图2所示系统框图,主要由信号处理单元、锁相环(Phase Locked Loop,PLL)、集成微带收发天线的压控振荡器(Voltage Controlled Oscillator,VCO)、透镜天线、中频滤波放大 电 路、模 数 采 集 控 制 器(Analog-to-Digital Converter,ADC)构成。

图2 雷达系统框图
MCU选择低功耗系列且自带12 b ADC模块,既可以实现整机低功耗,又提高了系统集成度节约电路板空间。由于太赫兹频段波长短,微带天线的设计对阻抗匹配要求很高,因此本方案采用集成片上天线的VCO芯片,配合透镜天线,可以实现波束聚焦功能,提高增益,波束角达到4°。PLL通过鉴相器构成闭环反馈回路稳定VCO输出信号频率。滤波放大电路中包含截止频率为50 Hz~2 kHz的带通滤波器和60 dB增益中频放大电路。
3 信号处理方法
3.1 离散频谱分析
雷达的中频信号的连续频谱S(f)中可以计算得到信号频率fd。通过对连续时间信号s(t)采样,得到离散时间信号s(n) :

离散信号的离散傅里叶变换(DiscreteFourier Transform,DFT)可以表示为

式中:WN=exp(-j2π/N)。DFT的频谱是离散的,可以看作是连续频谱的离散采样。频率和第k条频谱线之间的关系可以表示为Fk=Fs·k/N,其中,Fk表示对应的频率,Fs为信号采样率,N为采样点数,Fs/N为频率分辨率。由于“栅栏效应”,中频信号的频率fd不等于Fk,大多数连续频谱的最大值频谱处于DFT离散频谱最大值谱线和次大值谱线之间,因此直接从DFT频谱中提取出的信号频率误差范围为0.5·Fs/N,对应的测速误差为
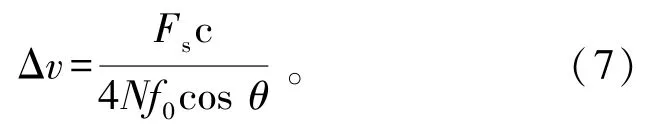
本文采用的0.12 THz频段雷达采用如下参数:f0=0.12 THz,Fs=20 kHz,N=1 024,θ=45°。带通滤波器截止频率设置对应的理论测速范围为0.088~3.5 m/s,测速误差为0.017 3 m/s,雷达一次测量周期为51.2 ms。从理论计算数据可以看出本文方案既可以保证满足地下管网测量范围和测流精度,同时工作时间短可以降低功耗。
3.2 多普勒频率估计算法
利用快速傅里叶变换(Fast Fourier Transform,FFT)计算回波频谱,计算当前帧IF信号权值最大的频率,进而计算当前流速。但实际上流体表面的流速不是单一流速波的结果[12],雷达回波信号是流体表面多种纹波的加权反射结果。由于多种速度回波信号进入雷达接收机,中频信号包含多种频率成分,导致频谱拓宽,不再是单一频率信号频谱。含有相近频率的中频信号频谱中最大值并不一定代表表面平均流速,可能是测量周期中某一时段表面波动比较大,有效RCS变大导致回波信号能量增加。因此,采用传统频谱细化算法不一定可以提高速度测量精度,反而有可能由于干扰导致测量误差偏大的情况,对于管道测流应用,更希望得到稳定、可靠、可信的流速结果,而不是追求可信度低的高精度流速。针对上述情况,本文提出一种多普勒谱中心频率估计的方法来估计多普勒频率大小。该方法能够有效滤除干扰噪声,提高信噪比,同时又能减小流速变化带来的测量结果抖动,同时结合速度统计滤波法获取稳定可靠的流速测量结果。
多普勒谱中心频率估计主要包括以下4个步骤:
(1)频谱平滑处理
由于原始回波信号中包含的频率成分比较复杂,频谱毛刺较多,容易造成后级主瓣提取错误,因此需要利用一定长度的低通滤波窗函数对频谱进行低通平滑滤波,窗函数的长度为频谱长度的十分之一。
(2)动态门限获取
频谱主瓣门限一般可以设置为-3 dB,本文采用峰值谱线前后两根谱线均值的一半作为频谱主瓣的动态门限,可以有效防止频谱最大值异常大或者异常小导致的偏差。
(3)频谱主瓣提取
以频谱峰值为分界线,向左搜索小于动态门限的第一根频谱线,对应的起始频率为fd0,向右搜索小于动态门限的第一根频谱线,对应的终止频率为fd1。
(4)计算频谱中心
多普勒中心频率等于上述提取的主瓣上限和下限的频率均值:fd=(fd0+fd1)/2。
图3为采集的中频信号FFT处理的频谱图,有较多频率成分。图4为经过频谱平滑处理后的频谱,红色线为动态门限,提取动态门限与平滑频谱的交点作为主瓣起始频率fd0和终止频率fd1。

图3 原始频谱图

图4 谱中心
3.3 速度统计滤波
在短时间内,液体流速不能发生突变,基本保持在一个速度范围内,但并不是一成不变的,同时由于雷达回波波束角比较小,随着液体表面波浪变化,回波信号能量波动动态范围大,强弱信号明显,导致不同测量周期内测量流速不一致,整体服从一定的概率分布[13-14],如图5所示,同时存在一些粗大误差结果。因此,本文提出一种速度统计滤波的方法,可以有效滤除粗大误差的同时获取测量时间范围内管道的平均流速。

图5 速度概率分布
3.2 节中多普勒谱中心频率估计可以获取多普勒频率fd,结合公式(4)中速度计算公式,为了方便在MCU中实现速度统计分布直方图,以cm/s为单位的整型速度数据

式中:floor()函数表示向下取整。重复N个周期可以获取N个速度测量值,并且记录速度Vj出现的次数为ni,其中N=∑ni。速度Vj出现的概率为ωi=ni/N。计算当前N个速度的均值和标准差分别为
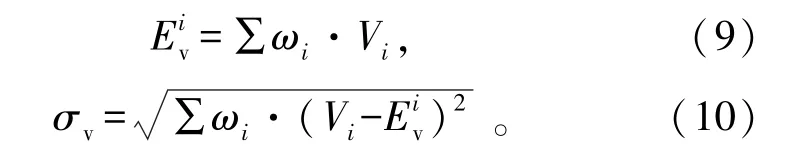
利用标准差作为门限滤除速度分布直方图中与均值偏差大于标准差的速度值,提取有效的速度值:

图6中,红色线表示均值,黄色线表示均值与标准差作为门限选取的有效速度分布值范围。
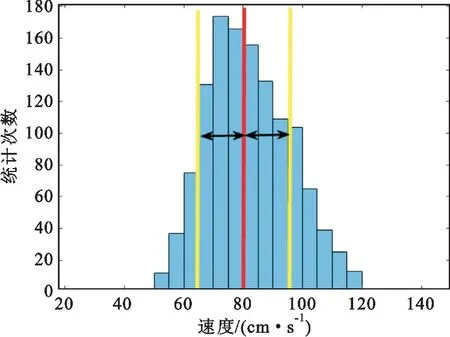
图6 速度直方图
速度Vj出现的次数为nj,其中M=∑nj,滤波之后速度Vj出现的概率为ωj=nj/M,滤波后的速度均值为

综上所述,以速度统计滤波后的速度均值作为观察时间范围内速度的平均值。
4 实验结果
根据图2所示的雷达系统框图设计0.12 THz雷达,如图7所示。该系统整机峰值功耗2 W,平均工作功耗10 mW,根据功耗要求通过调节信号发射占空比调整平均功耗大小,适合用于地下管网等环境下对功耗要求较高的应用场景。

图7 雷达电路板
由于地下管道存在一定的毒性,且测试安装协调难度大,本文为了验证算法可行性,选取河边作为测试点,并与接触式流速仪进行对比。

图8 河道实验
选取三个流速不同的点位进行试验,获取接触式测量结果和雷达测量结果进行对比,如表1所示。

表1 测量结果对比
根据表1中的测量结果对比可以看出,本次实验中,本文所设计的雷达系统和方法测量误差在2 cm/s范围内。
为了进一步说明该方法的测速可靠性,在华北水文仪器检测中心进行水槽试验,雷达固定安装于滑动平台车上,水槽运动过程中划桨搅动水面波动,试验过程中,平台车以一定的速度移动,水面不动,实现相对运动,将雷达测速结果与平台车运动速度进行对比,验证测量精度,如图9所示。结果表明,本雷达测速绝对误差小于3 cm/s,相对误差小于3%。华北水文仪器监测中心出具了相关测量误差报告。

图9 水槽实验及结果
通过河道实验和水槽实验结果可知,本文所提出的太赫兹雷达流速仪具有较高的测速精度,对相对速度和绝对速度都可以完成测量。
5 结束语
本文针对地下管道流速监测应用需求,提出一种多普勒谱中心频率估计法和速度统计滤波法来计算流速,可以有效滤除干扰噪声,提高信噪比,减小流速变化带来的测量结果抖动,进而获取稳定的流速测量值。为了验证该算法的可行性,设计了一套0.12 THz雷达系统,并且进行河道和水槽测试,与接触式流速仪测量结果对比,测量结果有效验证了本文算法的测速精度和可靠性。本文雷达系统和方法不受地下管网温度、湿度、腐蚀性等环境因素影响,同时功耗低、体积小,为地下管网流速监测提供了一种新的行之有效的监测方法。为进一步研究本雷达的可靠性,接下来的工作可以尝试在实际工况下安装本雷达进行长时间运行并记录其数据。

