累积结构特征描述的多模态遥感影像匹配*

谢勋伟

(中国西南电子技术研究所,成都 610036)

0 引 言

图像匹配实质是在具有一定重叠的影像间提取感兴趣共有特征的过程,是实现光束法平差、影像拼接与融合等应用的前提。受传感器成像机制、视角、时间及地物变化等影响,遥感影像间可能存在几何和辐射差异,为匹配算法带来了巨大挑战。目前,多模态图像匹配已成为研究的热点之一。

图像匹配方法主要分为区域匹配方法和特征匹配方法。区域匹配方法以局部图像信息为模板,遍历搜索窗口,计算每个位置的相似性度量,以某种测度作为特征对应的准则。特征匹配方法先提取显著的结构特征,再进行特征描述,最后通过描述子的距离衡量特征对应关系。它们的共性特点是在特征点提取或描述阶段采用了梯度信息,而多模态图像由于成像机制不同,图像间灰度存在显著的非线性差异,必然导致构造的特征描述符间也存在很大差异,由此造成其描述子的辨识能力较弱,产生大量错误匹配。

学者们研究发现,多模态图像虽然灰度差异较大,但图像结构细节信息具有高度相似性,可用于设计特征匹配。如Kovesi[1]提出了一种与图像强度无关的特征度量——相位一致性(Phase Congruency,PC),它对图像光照和对比度变化具有不变性,从而直接在PC图上提取角点和边缘具有明显优势。但PC图存在一定的局限:一是PC图大部分特征值为零,不利于特征描述;二是PC图包含强响应的孤立点,容易被噪声干扰,特征描述不够精确。李加元等人[2]提出的辐射不变特征变换方法(Radiation Invariant Feature Transform,RIFT)通过Log-Gabor[3]循环卷积序列构造多个最大指数图并以此构造描述子来获得旋转不变性,其实验显示该方法对多模态图像匹配的适应性大幅提高,但通过本文实验发现,该方法虽可以提高匹配点数量,但同时带来大量误匹配,其原因可能是最大指数图忽略了特征点局部邻域像素的空间结构,导致描述子的辨识能力有所下降。此外,在使用结构相似性进行多模态图像匹配领域,文献[4]采用图像的方向梯度构造了一种像素级的特征表达,在频率域采用三维快速傅里叶变换定义结构相似性测度以提升计算效率,可一定程度上适应辐射畸变,但它需要比较精确的初始匹配结果,适合在多模图像精匹配阶段使用。

近年来深度学习方法也逐渐引入到多模态医学图像匹配领域[5],但还未广泛应用到多模态遥感影像匹配领域[6]。受限于大规模遥感图像数据标注成本,采用深度学习方法完全取代人工描述子方法还不大现实,且迄今为止还未有不同模态图像间的深度网络训练模型高效迁移的成功范例。因此,人工描述子方法还有很大的潜力可挖,这也是本文的核心目的。

本文的基本思路是借鉴PC原理提取图像间的相似结构特征,利用结构特征构造描述子。为了增强图像的结构信息,克服PC图的局限,本文通过构造累积结构特征图(Cumulative Structural Feature,CSF)提升多模态图像间结构特征的相似性,并用其设计特征描述子。实验结果显示,本文方法可提高多模态遥感图像匹配的鲁棒性。

1 累积结构特征匹配方法

为了便于描述,将本文提出的特征匹配方法称为CSF方法,其实现流程如图1所示。

图1 CSF匹配流程图

1.1 多尺度多方向Log-Gabor奇对称滤波

二维Log-Gabor滤波器与人类视觉系统的度量一致,适于进行特征提取,可表示为[3]

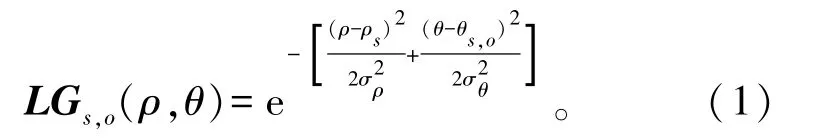
式中:(ρ,θ)表示极坐标;s和o表示Log-Gabor的尺度和方向;ρs和θs,o表示Log-Gabor的中心频率;σρ和σθ表示Log-Gabor在ρ和θ方向的带宽。

通过逆傅里叶变换将Log-Gabor滤波转换到空间域,得到二维Log-Gabor滤波表示:

式中:(x,y)表示空间域坐标;和分别表示Log-Gabor的偶对称滤波器和奇对称滤波器。

1.2 累积结构特征图构造和边缘特征点提取

式中:Es,o(x,y)和Os,o(x,y)分别为Log-Gabor偶对称滤波器和奇对称滤波器的滤波结果。

通过多尺度多方向的Log-Gabor滤波结果,并考虑噪声补偿,可得PC模型:

式中:Wo(x,y)为o方向的频率扩展权重;As,o(x,y)=表示图像幅值;ΔΦs,o(x,y)为相位偏差函数;T为噪声补偿;ε是一个极小的常数,防止分母为0。

PC图描述了图像的特征显著性,主要包含图像边缘结构和强响应角点,但其易受噪声干扰,因此,用PC图构造的特征描述子通常不大精确,辨识能力有限。有研究表明[7-8],Log-Gabor奇对称滤波器的滤波结果主要为图像上重复性更高的边缘,更适于不同模态图像的特征提取与匹配。而为了获得更加丰富的边缘结构特征,本文将多个尺度和方向的Log-Gabor奇对称滤波器的滤波结果进行信号平方和累加,以获得累积结构特征图:

为了消除CSF特征值绝对量的影响,将式(5)进行归一化,可得到最后的累积结构特征图模型:

CSF是一幅图像,其像素值表征了边缘结构的特征显著性。后续实验定性结果显示CSF图在细节和纹理上比PC图更丰富,非零元素大大减少,可有效克服PC图易受噪声干扰的问题,理论上更适于多模态图像的特征描述。

文献[9-10] 均依赖图像梯度提取特征点,在存在显著非线性辐射差异的图像上很难获得大量重复的特征点,不利于后续的特征匹配。Kovesi[11]通过对PC图进行协方差分析,分别在最大分量图和最小分量图上提取边缘点和角点。但最大分量图受Log-Gabor偶对称滤波结果影响,会潜在影响特征点的重复性。而本文在设计特征匹配方法时只考虑边缘结构,因为其对噪声点的敏感性更小。因此,后续实验中直接在只包含边缘结构的CSF图上采用FAST[12]方法进行特征点提取。

1.3 方向特征图构造

Kovesi[11]的模型中PC图的最小分量对应的轴即为特征点的方向,但该方向信息既有边缘结构的贡献,也有角点的贡献,后者中可能混有强响应的噪声,从而导致方向统计不够精确。而Log-Gabor奇对称滤波结果主要包含边缘结构特征,易于表达特征变化最显著的方向,从而表征特征的方向信息。通过多个尺度和方向的Log-Gabor奇对称滤波结果在水平和垂直方向的分量可计算CSF特征值的方向信息,计算方式如下:

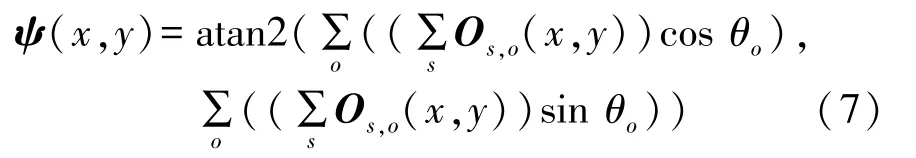
式中:ψ(x,y)的范围为[0,2π),ψ也是一幅图像,称为方向特征图。

1.4 特征描述符构造和特征向量匹配

结合梯度方向直方图的概念,在以边缘特征点为中心的邻域窗口内,利用高斯核函数对CSF特征值大小进行加权,计算CSF特征方向直方图,以直方图的峰值方向作为该特征点的主方向。CSF特征方向直方图的范围是0°～360°,每隔10°分为一柱。将边缘特征点局部邻域的坐标轴旋转到其主方向上,然后将邻域划分为N×N的图像块,每个图像块分为P个方向,从而形成局部CSF特征描述结构。对每个图像块内的CSF特征值进行方向直方图统计,再将所有直方图组合起来,形成N×N×P维的CSF特征描述向量。本文在后续实验中采用经验值(邻域半径取48,N取8,P取9),而在实际的工程应用中可根据遥感影像的分辨率或地物的丰富程度调整相应参数。

在特征匹配阶段,以往文献中通常采用最近-次近距离比阈值作为匹配判断准则,降低该阈值可增加匹配点正确率,但匹配点数量也会下降[13]。而该阈值设置往往依赖于经验或数据,如文献[13]和文献[14]中该阈值分别设置为0.8和0.6。为了避免阈值设置且尽可能保留更多正确的匹配点,本文采用最近距离准则和双向匹配策略进行特征匹配,获得一一对应的初始匹配点。

2 实验与分析

2.1 实验数据

本文选择深度图与可见光、红外与可见光、SAR与可见光、Google Map与可见光、光学-光学、夜光-白天等6种多模态遥感图像匹配场景,每个场景3组图像,共计18组数据进行实验,验证CSF方法的表现性能。如图2所示,左边是参考影像,右边是待匹配影像;每组图像中,每种场景选择一组图像显示。数据中主要存在微量的旋转和平移且无明显的尺度差异,但光谱差异大、非线性辐射差异明显。其中前三组图像比后三组图像更难匹配,因为其图像对之间的非线性辐射差异更加明显,对描述子的辨识能力要求也更高。

图2 部分实验数据

2.2 评估指标和实验细节

将CSF方 法 与SIFT[13]、SAR-SIFT[15]、LHOPC[10]和RIFT[2]进行对比,以成功匹配数(Success Number,SN)、匹配正确点数目(Number of Correct Number,NCM)、匹配正确率(Ratio of Correct Number,RCM)和运行时间作为评估指标。SIFT和SAR-SIFT选择文献中的默认参数运行。为了尽可能公平比较CSF、LHOPC和RIFT的表现性能,三者均在CSF图上提取不超过2 500个特征点,以保证特征点输入相同;同时主方向和描述符的计算方式及参数均相同,以保证三者的性能不受描述符局部区域大小和构造方式的影响,从而评估描述子的辨识能力。所有算法采用Matlab 2014a编程,运行环境为Inter(R) Core(TM) i7-6700HQ CPU@2.6 GHz和8 GB内存。

实验评估阶段,在原始图像上人工选择一定数量的控制点,以单应矩阵模型为约束,采用RANSAC方法[16]剔除粗差,保留模型残差小于3个像素的匹配点,并采用最小二乘对模型进行重估计,产生单应性模型真值。以最终匹配点坐标和模型真值计算同名点残差,将残差小于3个像素的匹配点视为正确点;若正确点个数小于4,则视为匹配失败。

2.3 非线性辐射差异匹配实验

上述五种方法的SN、平均NCM和平均NCR对比如表1所示,NCM运行时间对比如表2所示。表1中“F”表示该场景下三组数据均匹配失败,而匹配失败的案例不参与NCM和RCM计算。

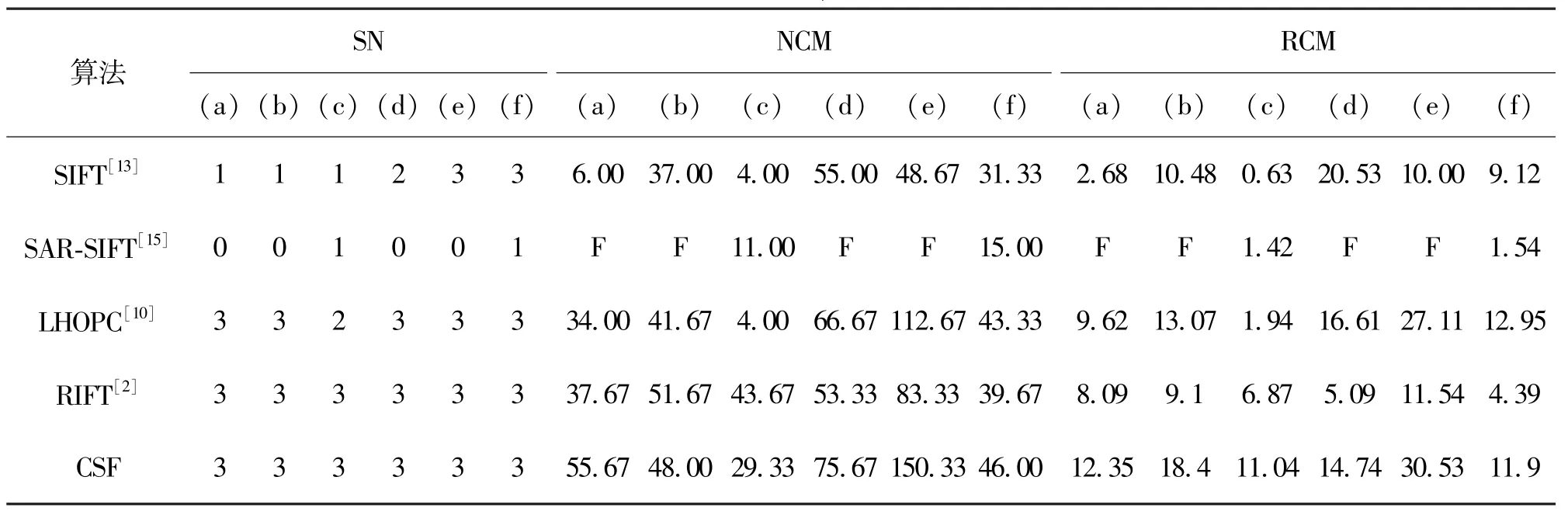
表1 五种算法的成功匹配数、平均NCM和RCM对比

表2 五种算法的平均运行时间

由表1可知,SIFT有7对图像匹配失败,成功率为61%,且前三种场景的匹配成功率低于后三种场景,说明SIFT对于少量的非线性辐射差异也具有一定的抗性,但对存在显著非线性辐射差异的图像中很难提取到高度相似的描述子,容易造成大量误匹配。SAR-SIFT仅在两对图像上匹配成功,成功率仅为11%,且其匹配点数和正确率均极低,说明SAR-SIFT改进的梯度计算方式仍然不能保证提供稳定的特征显著性表达,以此计算的特征描述符也不够稳健,因此对于存在显著强度和对比度差异的场景适应性能很差。而基于结构信息设计且原理基本相似的三种描述子LHOPC、RIFT和CSF在6种场景中的匹配成功率分别为94%、100%和100%,间接说明采用图像结构的显著性特征来进行多模态图像匹配比直接采用梯度信息更有优势。前三种场景中,RIFT的NCM要明显优于LHOPC,说明RIFT比LHOPC具有更强的正确匹配召回性能;但RIFT的平均NCR要低于LHOPC,说明RIFT匹配结果中混合大量的误匹配,其描述子的辨识能力反而不如LHOPC。而本文提出的CSF方法在平均NCM和NCR上均要优于LHOPC和RIFT,说明本文采用的累积结构特征图设计描述子要优于PC图,同时累积结构特征图也克服了最大指数图辨识能力不足的局限。

由表2可知,平均运行时间上,CSF方法要优于SIFT、SAR-SIFT和RIFT,但与LHOPC的运行时间相当。其原因是SIFT和SAR-SIFT需要构造尺度空间,而RIFT需要构造循环描述子以克服最大指数图受构造顺序影响的缺陷。CSF方法理论上具有LHOPC一致的计算复杂度,其时间消耗均主要集中在多个尺度和方向的结构信息提取及描述子计算两个环节,在实际应用中可C++编程结合并行加速技术以提高计算效率。

为了定性分析CSF和LHOPC性能差异的本质原因,图3给出了图2(c)中SAR和可见光图像的PC图和CSF图。直观上可以看出,CSF图上主要为边缘结构,而PC图上包含边缘结构和孤立点(含噪声),而孤立点更容易造成同名点描述子的巨大差异,降低描述子的辨识能力;CSF图上非零元素明显多于PC图,用其构造描述子也更精确。

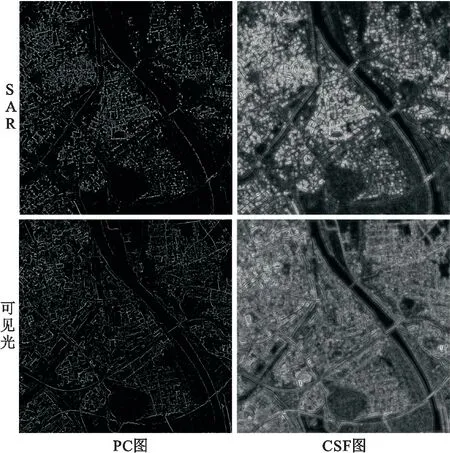
图3 图2(c)中的PC图和CSF图对比

图4为本文方法的匹配结果,可见匹配点分布比较均匀,可用于后续图像拼接、镶嵌等常规遥感图像数据处理任务。

图4 本文方法对于图2数据的匹配结果

3 结束语

针对相位一致性模型在具有非线性辐射差异的多模态遥感影像特征匹配中非零信息少且易受噪声干扰而导致特征描述能力有限的问题,本文提出了一种累积结构特征图构造和特征描述子建立的新方法。相比PC图,累积结构特征图所含非零信息明显增多,提高了多模态图像的结构相似性,直接用于特征提取和描述可有助于获得高度重复的特征对应,增强匹配成功性。实验结果表明,相比SIFT、SAR-SIFT、基于PC图的LHOPC和RIFT,本文方法在匹配成功率、平均正确匹配数目和正确率上均有明显的提升,说明了本文方法的有效性。

本文方法暂无法适应重复纹理或无纹理结构,对于弱纹理结构,可通过边缘增强技术提高其成功率。在实际应用中,特征匹配阶段可采用最近一次近距离阈值比准则提高匹配正确率。笔者通过前期实验,该阈值设置为0.95可大幅剔除误匹配,提高初始匹配正确率,供读者参考。后续研究中可将高精度的特征检测子与本文的描述子相结合,同时扩展对大尺度差异的适应性。