一类多重循环群的宽度
雒晓良, 刘合国
(1. 太原师范学院数学系, 山西 晋中 030619; 2. 海南大学理学院, 海口 570228)
本文采用标准的术语和符号参照文献[1].
若群G存在长度有限的正规列, 其商因子均为秩小于等于n的Abel群, 且n为满足该条件的最小自然数, 则称G的宽度为n, 称G为Bn-群.显然,Bn-群的子群和商群的宽度不超过n.群的宽度备受关注[2-7], 但研究进展缓慢.称G为多重循环群, 如果G是满足子群极大条件的可解群, 这等价于G具有一个次正规群列G=G0>G1>…>Gn=1, 其中每个Gi/Gi+1都是循环群.对于多重循环群宽度的研究, 基本思路是研究给定宽度的群的结构.如B1-群即超可解群; 樊恽[8]研究了B2-群的正规列及一些特殊条件的B2-群.但当多重循环群的宽度大于2时, 研究变得非常困难.因此, 另一种思路是通过讨论给定群的宽度, 进而推导出其他群的宽度.笔者[9-10]巧妙地利用循环置换在Abel群上的自同构作用和半直积构造了一类多重循环群, 并得到了这类群详细的剩余有限性质, 以及这类群的同构刻画, 这些结果对经典结论[1]做了很好的解读: 若存在无限多个素数p使得多重循环群是剩余有限p-群, 则该群是一个无挠幂零群.本文拟采用第二种思路,研究一类具有特殊意义的多重循环群的宽度.
1 主要结果
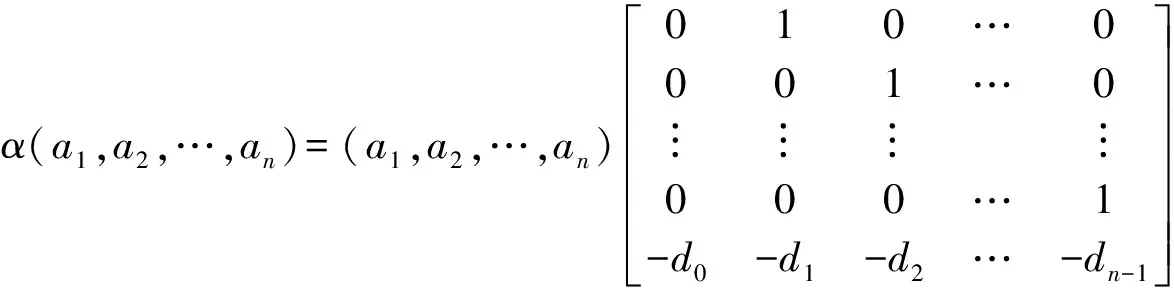
引理1[9]1) 若f(λ)没有整数根, 则A中不存在秩为n-1的α-不变子群;
2) 若f(λ)不可约, 则A中不存在非平凡的α-不变子群A0, 其中A0的秩小于A的秩.
对于如上定义的自由Abel群A, 取γ∈Aut(A)使得
则γ(ak)=ak+1(k= 1,2,…,n-1),γ(an)=-r0a1-r1a2-…-rn-1an.令h(λ)=|λI-γ|, 则下面引理描述了A中γ作用不变的直和形式的子群.
引理2若h1(λ)是Z上的s次多项式且在Z[λ]上整除h(λ),0≤s≤n-1,则
A=〈a1〉⨁〈a2〉⨁…⨁〈as〉⨁〈h1(γ)a1〉⨁〈γh1(γ)a1〉⨁…⨁〈γn-s-1h1(γ)a1〉,
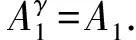
证明 因h1(λ)|h(λ), 存在h2(λ)∈Z[λ]使h(λ)=h1(λ)h2(λ), 式中h2(λ)是n-s次多项式.设h1(λ)=λs+bs-1λs-1+…+b0及h2(λ)=λn-s+cn-s-1λn-s-1+…+c0,有
则(a1,a2,…,an)P=(a1,…,as,h1(γ)a1,…,γn-s-1h1(γ)a1), 式中
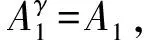
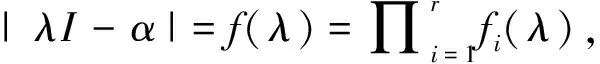
故

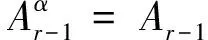

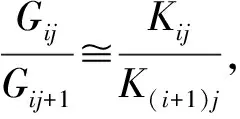

对于多重循环群,B1-群即是超可解群, 由此易推出文献[9]中定理2.1(1).
推论1G是超可解群当且仅当|λI-α|=(λ-1)i(λ+1)j,i+j=n,i,j∈N.
证明 由定理1可知G是超可解群当且仅当G的宽度为1, 即f(λ)=|λI-α|是一次多项式的乘积.注意到|λI-α|=λn+dn-1λn-1+…+d1λ+d0中d0=±1, 显然f(λ)=|λI-α|是一次多项式的乘积当且仅当|λI-α|=(λ-1)i(λ+1)j,i+j=n,i,j∈N, 证毕.
2 应用
下面讨论特殊情形f(λ)=λn-mλn-1±1(n≥2)时G的超可解性.利用Rouche定理和文献[11]中定理(1.1.1), 可得多项式f(λ)在Q上的不可约性[9], 即: i) 若|m|≥3, 则f(λ)在Q上不可约; ii)λn-2λn-1-1在Q上不可约; iii) 若n是偶数, 则λn+2λn-1-1在Q上不可约; iv) 若n是奇数, 则λn+2λn-1+1在Q上不可约.基于这些结论及多重循环群宽度的判定定理, 可得下述情形下G的超可解性.
定理21) 当f(λ)=λn-mλn-1+1时,G是超可解群当且仅当m=±2 且n=2;
2) 当f(λ)=λn-mλn-1-1时,G是超可解群当且仅当m=0且n=2.
证明 充分性显然, 故仅证必要性.若G是超可解群,由推论1知, 当|λI-α|=(λ-1)i(λ+1)j,i+j=n,i,j∈N, 由上面多项式的不可约性知m=0,±1,±2.
1) 对f(λ)=λn-mλn-1+1.若m=0, 有f(λ)=λn+1, 而λn+1显然不可能分解为若干个λ-1和λ+1的乘积, 矛盾; 若m=±1, 有f(λ)=λn±λn-1+1, 而λn-mλn-1+1若存在有理根, 则根只可能为±1, 经验证, ±1都不是根, 故f(λ)不能分解为若干个λ-1和λ+1的乘积, 矛盾.因此m=±2, 即f(λ)=λn±2λn-1+1.对于λn+2λn-1+1, 由不可约性知n为偶数, 显然1不是λn+2λn-1+1的根, 故只能f(λ)=(λ+1)n, 此时必然有n=2; 对于λn-2λn-1+1, 由韦达定理知所有根的和为2=λ1+λ2+…+λn, 即根为1和-1的出现次数相差2, 故n必为偶数.而-1显然不是λn-2λn-1+1的根, 有f(λ)=(λ-1)n, 此时必然有n=2.
2) 对f(λ)=λn-mλn-1-1.若m=±1, 有f(λ)=λn±λn-1-1, 则λn-mλn-1-1若有有理根, 根只可能为±1, 经验证, ±1都不是根, 故f(λ)不能分解为若干个λ-1和λ+1的乘积, 矛盾; 若m=2, 有f(λ)=λn-2λn-1-1, 由多项式的结论, 知λn-2λn-1-1在Q上是不可约的, 矛盾; 若m=-2, 有f(λ)=λn+2λn-1-1, 由不可约的结论知n为奇数, 显然-1不是λn+2λn-1-1的根, 故f(λ)=(λ+1)n, 展开对比多项式常数项即得矛盾.因此, 只能m=0, 有f(λ)=λn-1,又f(λ)=(λ-1)i(λ+1)j, 必然有n=2, 证毕.
文献[10]中关于定理3.1的证明,利用了超可解群的定义以及分析了元素的幂自同构作用,而本文利用多重循环群的宽度, 极大地简化了证明步骤,并对该定理进行了推广.

