Fault-tolerant finite-time dynamical consensus of double-integrator multi-agent systems with partial agents subject to synchronous self-sensing function failure
Zhi-Hai Wu(吴治海) and Lin-Bo Xie(谢林柏)
Engineering Research Center of Internet of Things Technology Applications of MOE,School of Internet of Things Engineering,Jiangnan University,Wuxi 214122,China
Keywords: multi-agent systems,synchronous self-sensing function failure,finite-time dynamical consensus,network topology connectivity recovery
1. Introduction
During the past twenty years, consensus of multi-agent systems (MASs), owing to its wide applications in multiple robot systems,wireless sensor networks,intelligent transportation systems,smart grids,social networks,and so on,has received a lot of attention from researchers in different disciplines. Consensus means that all agents under distributed control inputs called consensus protocols eventually reach a common value. According to different convergence time,consensus is divided into asymptotical and finite-time consensus. Compared with asymptotical consensus,[1–8]finite-time consensus possesses more advantages such as faster convergence rate,better disturbance rejection,and robustness to uncertainties. Also,in real application,an agent,such as an underwater robot and an unmanned aerial vehicle, is controlled for its desired motion by its acceleration rather than by its speed. Therefore, finite-time consensus problems of doubleintegrator MASs have been well studied.[9–14]
Notice that successful implementation of all of the finitetime consensus protocols in Refs.[9–14]depends on the availability of the position and velocity state errors between an agent and its local neighbors. In general,to compute the state errors,an agent has to measure its own absolute states by satellite positioning systems such as GPS.However,in some complex work scenarios, it is hard for an agent to obtain its own absolute states based on satellite positioning systems. For example, a group of unmanned aerial vehicles are required to keep a particular formation, get into a thick forest, and complete a task of extinguishing a fire. Once a vehicle gets into the forest,which can be regarded as a typical indoor environment, its own absolute position and velocity states will be no longer measured by GPS.In this situation,the vehicle that has got into the forest is called to suffer from self-sensing function failure(SSFF).If the vehicle subject to SSFF is not controlled by a new measure, it will no longer keep the particular formation with other vehicles, which might result in the loss of timely completing the task of putting out the fire. One can see from this example that once an agent suffers from SSFF,its absolute states can be no longer measured by its sensors,making the state errors between itself and its local neighbours unavailable and further making itself unable to be controlled in a closed-loop manner. If an agent subject to SSFF is not given a novel control scheme,it cannot achieve consensus with other normal agents. Moreover,if an agent suffers from SSFF,its neighbours can no longer obtain its states in spite of keeping communicating with it. Hence,the occurrence of SSFF at an agent might destroy the connectivity of network topology among normal agents in the sense of obtaining information.If the connectivity of network topology among normal agents is not recovered, the subsystems composed of normal agents cannot reach consensus, let alone the whole MASs. In summary,SSFF can destroy the achievement of consensus among the whole MASs.
Therefore, we need to find an appropriate strategy of recovering the connectivity of network topology among normal agents and a proper fault-tolerant finite-time consensus protocol to ensure that double-integrator MASs with partial agents subject to SSFF can still reach finite-time consensus. As far as we know, there is no open result on fault-tolerant finite-time consensus of double-integrator MASs with partial agents subject to SSFF.
Based on the above considerations, in this paper we investigate the fault-tolerant finite-time consensus problems of double-integrator MASs with partial agents subject to SSFF.First, a strategy of recovering the connectivity of network topology among normal agents is proposed based on multihop communication together with agents subject to SSFF as routing nodes. Second, a fault-tolerant finite-time dynamical consensus protocol with time-varying gains is proposed.Third, convergence analysis is made in theory. Last, numerical simulations are provided to illustrate the effectiveness of the theoretical results.
The main innovations of this paper are summarized as follows. First, different from sensor faults in Refs. [15–19],where the states or outputs of an agent mixed with sensor faults can be directly measured for designing consensus protocols,SSFF discussed in this paper means that if an agent suffers from SSFF, its states can be no longer directly measured for designing consensus protocols. Second, unlike the research idea on dynamical network topology in Ref. [20], where the conditions on dynamical network topology guaranteeing consensus are derived from the perspective of analysis,the method of actively recovering the network topology connectivity is proposed in this paper. Third, different from the consensus protocols in Refs.[9–14],where a closed-loop control scheme is always put on each agent, a fault-tolerant finite-time consensus protocol is proposed to cope with SSFF in this paper,where an agent is controlled in a closed-/open-loop manner before/after suffering from SSFF,respectively.
The rest of this paper is organized as follows. In Section 2, some preliminaries are provided and the problem is formulated. The strategy of recovering the connectivity of network topology among all normal agents is proposed in Section 3. The fault-tolerant finite-time dynamical consensus protocol is presented, and its effectiveness to guarantee finite-time dynamical consensus is demonstrated theoretically in Section 4. Numerical simulations are provided to illustrate the effectiveness of the theoretical results in Section 5. Conclusions with future research directions are included in Section 6.
2. Preliminaries and problem formulation
2.1. Algebraic graph theory


2.2. Problem formulation
For MASs withNagents, agentiand the available information flow between agentiand agentjare regarded as nodeviand edgeeijin an undirected graphG, respectively.For double-integrator MASs, the dynamics of agentican be described by

i.e., reach finite-time dynamical consensus, where sgn(·) is the sign function,σ ∈(0,1), andTis a finite time relying on(pi(0),qi(0)),i ∈I.
Definition 1 Agentiwith double-integrator dynamics(1)is called to suffer from SSFF att+i,if its position statepi(t)and velocity stateqi(t)can be measured only in[0,ti]but cannot be done in(ti,+∞),where 0≤ti<+∞.
One can see from Eqs.(1)and(2)that to reach finite-time dynamical consensus among the whole MASs, agentineeds to get the states(pj(t),qj(t))of its neighboursj ∈Niand its own states(pi(t),qi(t)). However,just as we said above,once agentisuffers from SSFF, the closed-loop control scheme in Eqs.(1)and(2)can be no longer carried out,and the connectivity of network topology among normal agents might be destroyed,leading to the loss of finite-time dynamical consensus among the whole MASs.
In the following, we will propose a strategy of recovering the connectivity of network topology among normal agents and a fault-tolerant finite-time dynamical consensus protocol to tackle SSFF and simultaneously guarantee the achievement of finite-time dynamical consensus among the whole MASs.
Before moving on, we need to present the following assumptions.
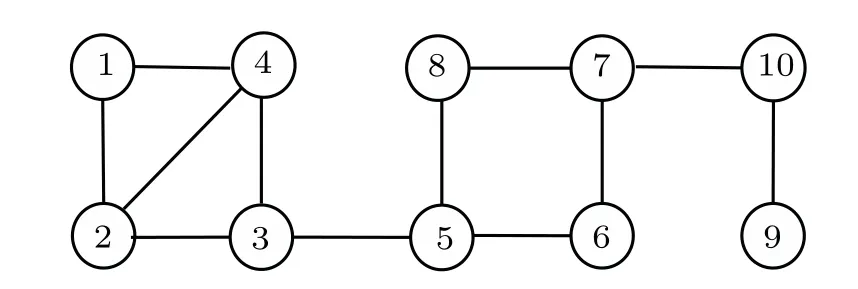
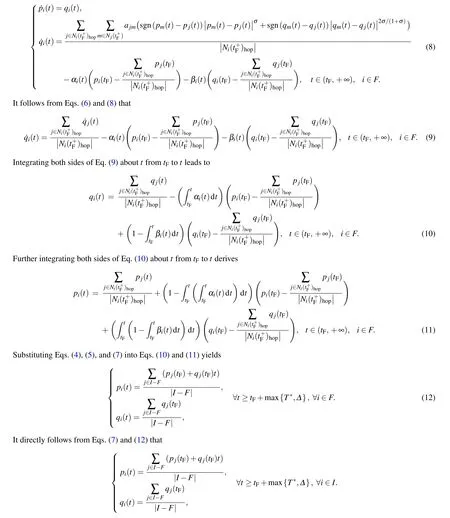
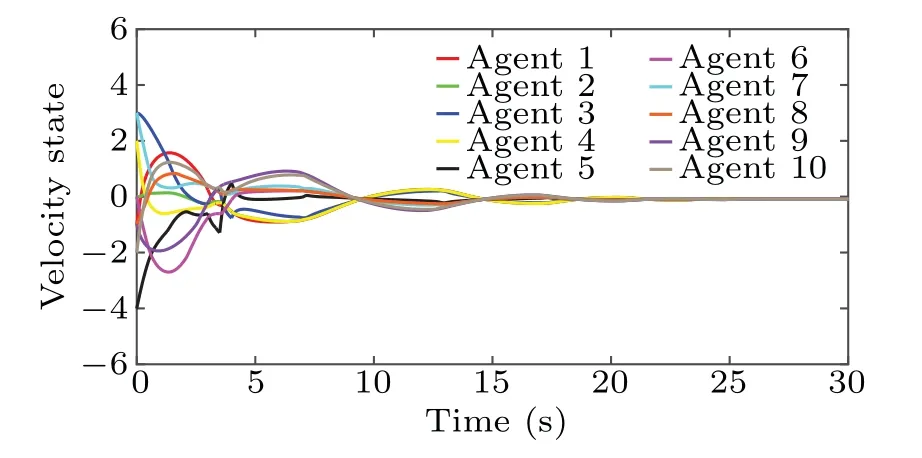
Assumption 1 SSFF is synchronous,i.e.,tF≜ti=tj,t+F≜t+i=t+j,∀i,j ∈F,whereFrepresents the set of all agents subject to SSFF,and the number|F|of agents subject to SSFF satisfies 1≤|F| Assumption 2 The network topology before SSFF is fixed,undirected,and connected,and there is no factor bringing about the change of network topology except SSFF and carrying out the strategy of recovering the connectivity of network topology among normal agents to be presented. In this section, a strategy of recovering the connectivity of network topology among normal agents is proposed,where Assumption 1 and Assumption 2 are satisfied. A specific example is used to better show the processes of the network topology connectivity recovery. For MASs with ten agents and the initial network topology shown in Fig. 1, without loss of generality, assume that agents 3,5,10 suffer from synchronous SSFF att+F. Fig.1. Network topology among all agents in[0,tF]. Att+F, because agent 3 can no longer measure its own states by its own sensors,agent 3 knows that itself suffers from SSFF and immediately relays the states received from agent 2,agent 4,and agent 5 to agents 4,5,agents 2,5,and agents 2,4, respectively. However, because agent 5 also suffers from SSFF att+F,agent 3 cannot receive the states of agent 5,knows that agent 5 also suffers from SSFF,informs agent 5 to repay the states received from agents 6, 8 to it,i.e., agent 3, and immediately relays the states received from agent 2, agent 4,agent 6, and agent 8 to agents 6, 8, agents 6, 8, agents 2, 4,8, and agents 2, 4, 6, respectively. For agents 5, 10 subject to SSFF att+F,similar procedures are implemented simultaneously. It follows from the above procedures that when agents 3, 5, 10 suffer from synchronous SSFF att+F, new undirected edges (v2,v6), (v2,v8), (v4,v6), (v4,v8), (v6,v8), and (v7,v9)are added to the network topology among normal agents from the viewpoint of obtaining information,where multi-hop communication technology together with agents 3,5,10 as routing nodes is utilized. For these newly added edges, without loss of generality, all of their weights are set as 1. The new network topology among normal agents shown in Fig.2 is established via the above procedures,which is obviously connected in(tF,+∞). Fig.2. Network topology among normal agents in(tF,+∞). For general cases, it is obvious that under Assumption 1 and Assumption 2, the above strategy of recovering the connectivity of network topology among normal agents can guarantee that the new network topology among normal agents is connected in(tF,+∞). For the convenience of the following expression, we present the following definitions. Definition 2 SetV′is called maximum failure connected subset(MFCS)of graphG,if the following conditions are simultaneously satisfied: (i)V′⊆F;(ii)when any normal node is not used as a routing node,any two distinct nodes ofV′are connected; (iii) when any normal node is not used as a routing node,∀vi ∈F −V′,∀vj ∈V′,nodeviand nodevjare not connected. According to Definition 2,Gin the above example only has two MFCSs,i.e.,{v3,v5}and{v10}. Definition 3 SetV′′is called maximum normal neighbor set(MNNS)of MFCSV′,ifV′′is only composed of all normal neighbor nodes of each node in MFCSV′. According to Definition 3,{v2,v4,v6,v8}and{v7,v9}are MNNSs of MFCSs{v3,v5}and{v10},respectively. According to Definition 4,MHNNSs of nodev3,nodev5,and nodev10are{v2,v4},{v6,v8},and{v7,v9},respectively. Remark 1 The core of the above strategy of recovering the connectivity of network topology among normal agents is to use multi-hop communication technology together with all agents subject to SSFF as routing nodes for reconnecting any two distinct nodes of each MNNS and ensuring that the subgraph composed of all nodes in each MNNS is a complete graph. Remark 2 Multi-hop communication technology has been successfully used in topology control and routing protocol design of wireless sensor networks, which are typical MASs, and has been used for designing consensus protocols of MASs to improve the convergence rate of achieving consensus in Refs.[21–25]. Besides,when the number of agents in an MFCS is not large,carrying out the proposed strategy of network topology connectivity recovery will not quite damage the distributed property of MASs. In this section,a fault-tolerant finite-time dynamical consensus protocol is proposed for double-integrator MASs with partial agents subject to synchronous SSFF and its effectiveness to ensure finite-time dynamical consensus is theoretically demonstrated. For double-integrator MASs(1)satisfying Assumption 1 and Assumption 2, we propose the following fault-tolerant finite-time dynamical consensus protocol: Theorem 1 Under Assumption 1 and Assumption 2,double-integrator MASs(1)applying the proposed strategy of recovering the connectivity of network topology among normal agents and the fault-tolerant finite-time dynamical consensus protocol (3) reach finite-time dynamical consensus, provided that where∆is a positive constant that can be arbitrarily chosen. Proof Substituting Eq.(3)into Eq.(1)gives the closedloop model of agenti(i ∈I −F)in(tF,+∞)as follows: whereT∗is a finite time relying on(pi(tF),qi(tF)),i ∈I −F. Substituting Eq.(3)into Eq.(1)can also yield the open-loop model of agenti(i ∈F)in(tF,+∞)as follows: This means that double-integrator MASs (1) under the proposed strategy of recovering the connectivity of network topology among normal agents and the fault-tolerant finitetime dynamical consensus protocol(3)achieve finite-time dynamical consensus. The proof is completed. Remark 3 The effectiveness of the fault-tolerant finitetime dynamical consensus protocol (3) depends on the existence ofαi(t)satisfying condition(4)andβi(t)satisfying condition (5). It is easy to see that any constant gain does not satisfy condition (4) or condition (5). Fortunately, bothαi(t)satisfying condition (4) andβi(t) satisfying condition (5) really exist. It can be verified that in Eq.(3)is to compute control inputuj(t)(t ∈(tF,+∞))of agentj(j ∈Ni(t+F)hop) by agenti(i ∈F). For agenti(i ∈ F), both of (pj(t),qj(t)) (j ∈Ni(t+F)hop) and (pm(t),qm(t))(m ∈Nj(t+F)), which are need while computing control inputuj(t)(t ∈(tF,+∞)),can be obtained by using multi-hop communication technology together with partial or all agents in an MFCS where agenti(i ∈F) is located as routing nodes.Similarly,when the number of nodes in an MFCS is not large,implementing the fault-tolerant finite-time dynamical consensus protocol(3)will not quite damage the distributed property of MASs. Consider double-integrator MASs with ten agents and the initial network topology shown in Fig.1. Without loss of generality,all weights of edges are 1,the initial states of all agents are randomly set,and agents 3,5,10 suffer from synchronous SSFF withtF=3 s. The new network topology among normal agents shown in Fig. 2 is constructed by using the proposed strategy of network topology connectivity recovery. Numerical results of double-integrator MASs (1) under protocol (3)withα3(t)=α5(t)=α10(t)in Eq.(13),β3(t)=β5(t)=β10(t)in Eq.(14),∆=3,andσ=0.5 are shown in Figs.3 and 4.It is easy to see from Figs.3 and 4 that double-integrator MASs(1)using the fault-tolerant finite-time dynamical consensus protocol (3) achieve finite-time dynamical consensus. Therefore,the results of Theorem 1 are numerically verified. Fig.4. Velocity states of systems(1)under protocol(3) This paper studied the fault-tolerant finite-time dynamical consensus problems of double-integrator MASs with partial agents subject to synchronous SSFF. The strategy of network topology connectivity recovery and the fault-tolerant finite-time dynamical consensus protocol were proposed for resisting SSFF.Theoretical and numerical results showed that double-integrator MASs with partial agents subject to synchronous SSFF using the strategy of network topology connectivity recovery and the fault-tolerant finite-time dynamical consensus protocol can reach finite-time dynamical consensus. It should be noticed that SSFF was assumed to be synchronous in this paper. However, in real application, SSFF might be asynchronous. Therefore, in the future, we will investigate fault-tolerant finite-time dynamical consensus of double-integrator MASs with partial agents subject to asynchronous SSFF. Acknowledgements Project supported by the National Natural Science Foundation of China (Grant No. 61876073) and the Fundamental Research Funds for the Central Universities of China (Grant No.JUSRP21920).3. Network topology connectivity recovery


4. Fault-tolerant finite-time dynamical consensus protocol and convergence analysis

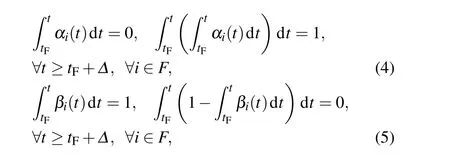
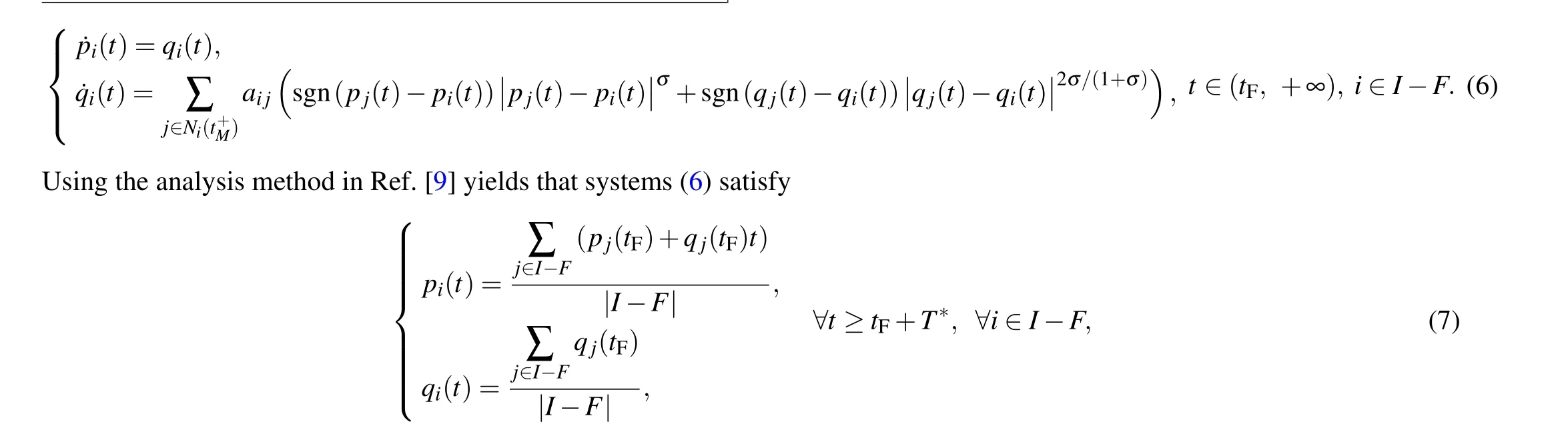

5. Numerical simulations
6. Conclusions
- Chinese Physics B的其它文章
- Nano Ag-enhanced photoelectric conversion efficiency in all-inorganic,hole-transporting-layer-free CsPbIBr2 perovskite solar cells
- Low-voltage soft robots based on carbon nanotube/polymer electrothermal composites
- Parkinsonian oscillations and their suppression by closed-loop deep brain stimulation based on fuzzy concept
- Temperature dependence of spin pumping in YIG/NiO(x)/W multilayer
- Interface effect on superlattice quality and optical properties of InAs/GaSb type-II superlattices grown by molecular beam epitaxy
- High-sensitive phototransistor based on vertical HfSe2/MoS2 heterostructure with broad-spectral response

