基于改进灰狼算法的梯级电站中长期优化调度

黄显峰，钱 骏，颜山凯，吴志远，刘志佳

(1.河海大学水利水电学院，江苏 南京 210024;2.华电福新能源股份有限公司池潭水力发电厂，福建 泰宁 354400)

0 引 言

梯级电站通过联合调度形成大型水电能源基地，比单一调度更能保障水资源的利用效率[1]，其中龙头电站的调节能力可以提升下游电站的调蓄水平，进而提升水电系统运行效益[2]。然而随着系统规模的不断增长，上下游水力和电力联系使得约束变得更为复杂，如何降低计算复杂度成为了难点问题。针对“维数灾”问题，粒子群算法、遗传算法等启发式智能算法得到了广泛应用；对于求解过程易发生早熟收敛、解的随机波动性较大的特点，通过改进优化调度方法，可以缓解局部收敛[3]与结果随机问题[4]。但约束环境与决策变量的复杂化使得计算量呈指数型增长，具体表现为可行域的空间搜索过程中，一是寻优过程难以跳出当前环境，二是产生大量不可行解，影响了求解效率与优化程度。

针对上述问题，通过阶段变量分段与决策变量预处理，可以有效提升求解效能。例如，吴志远等[5]通过在粒子群算法中引入分段和特殊变异操作，提升了进化过程中解的质量及算法的搜索效率；方国华等[6]通过在混合蛙跳算法中引入自适应差分算法加快个体寻优，得到了收敛性与分布性更好的方案；于梅赞等[7]通过在粒子群算法中引入“双适应度”排序方式，先按照约束性适应度进行排序，再按照优化目标进行排序，有效保留了优良个体。

然而面对约束环境复杂且决策变量相互联动的水库调度问题，需要根据库容变化的影响采取相应的改进措施，才能克服可行域搜索困难的问题。本文以灰狼算法[8]为切入点，针对跳出局部解与可行域搜索，引入“当前搜索解的空间识别”机制，并将其应用于梯级水库中长期优化调度问题中，验证了其有效性及工程实用性。

1 调度模型

1.1 目标函数

1.1.1 约束破坏度最小

约束破坏度的组成为：一是发生约束破坏的阶段变量数量，二是决策变量发生破坏的相对幅度。约束破坏度越小，越有利于可行解的确定。通过调度周期内的阶段变量约束破坏比例与幅度，获得不可行解的约束破坏度，计算式为

(1)

(2)

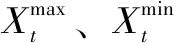
1.1.2 发电量最大

电站效益评价中，发电量是主要因素，以梯级电站总发电量最大为目标，计算式为

(3)

式中，F2为流域内梯级电站总发电量；I为电站总数；i为当前计算的电站；Ai为i电站的出力系数；Qi，t为i电站t时段的发电流量；Hi，t为i电站t时段的发电水头；Δt为计算步长。

1.2 约束条件

水库调度一般以电站水位、流量、出力、水量平衡、水力联系等条件作为约束，具体见文献[5]所述，本文不再赘述。由于发电流量直接影响电站运行安全与弃水问题，因此将超出上限的流量视为弃水，未达下限且大于0的按照下泄流量下限计算，计算式为

(4)

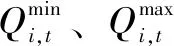
2 模型求解

2.1 传统灰狼算法

灰狼算法模拟狼群搜索捕猎的过程，将种群中最优的3个个体依次命名为α、β、δ，代表灰狼种群中处于领导阶级的3头狼；其余候补个体为ω。通过包围猎物、捕猎等操作求解问题，已经广泛应用于特征子集选择[9]、多输入输出电力系统[10]等方面。

(1)包围猎物。在灰狼个体确认自己和猎物的距离后，会预测猎物的移动并向其靠近，将狼群的这种行为称为“包围猎物”，计算式为

D=|CXp(n)-X(n)|

(5)

X(n+1)=Xp(n)-AD

(6)

A=2ar1-a

(7)

C=2r2

(8)

式中，D为灰狼个体与猎物之间的距离；A、C为参数；n为迭代次数；Xp(n)为第n代的猎物位置；X(n)为第n代灰狼的位置向量；a为收敛系数；r1、r2为0～1之间的随机值。

(2)捕猎。由于最优解位置未知，认为领导阶级的α、β、δ更接近猎物，ω狼不需要直接寻找猎物，而是向三者位置的中心值靠近来完成捕猎，计算式为

Di(n)=|CiXi(n)-X(n)|

(9)

i=α，β，δ

(10)

(11)

(12)

式中，Dα、Dβ、Dδ分别表示α、β、δ和其他个体的距离；Xα、Xβ、Xδ分别表示α、β、δ的当前位置。

2.2 当前搜索解的空间识别机制

传统灰狼算法具有较强的收敛性能，但在寻找可行解的过程中忽视了目标全局性能，同时在寻优过程中难以兼顾多个目标同步优化。针对上述问题，根据当前搜索解的约束破坏度，引入空间识别机制，用以跳出当前环境并趋近可行域，计算步骤为：

(1)设置搜索参数，包括优化对象、迭代次数、搜索目标、退出条件等。

(2)随机选取调度周期内的计算时段，判断该时段的约束破坏度。如果约束破坏度大于0，进入步骤3；否则进入步骤4。

(3)根据约束破坏度储存信息识别当前时段决策变量的可行域，通过可行域的空间识别驱动决策变量向可行域移动，计算式为

(13)

式中，r1～r7为0～1之间的随机值，表示驱动当前时段决策变量的移动幅度；e为驱动参数，表示当前时段决策变量的移动方向，破坏下限时e取1，破坏上限时取-1。

(4)根据相邻时段的约束破坏信息对当前时段的决策变量进行调整，减小相邻时段因该时段决策变量变化而发生破坏的可能性，计算式为

(14)

图1 改进灰狼算法流程

式中，r8为0～1之间的随机值，当前后时段都破坏上限时e取-1，都破坏下限时e取1，其他情况e取0。

(5)重复步骤(2)～(4)，达到最大迭代次数后，比较当前搜索解与原先解。当前搜索解的约束破坏度不高于原先解时，视为非劣于原先解；若同时目标发电量大于原先解，则替换为当前搜索解，否则返回原先解。

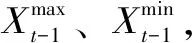
(15)

2.3 求解流程

图1所示为改进灰狼算法的求解流程，虚线框内为传统灰狼算法的运算过程。改进灰狼算法在更新α、β、δ位置后，并不直接进行ω狼的位置移动，而是先根据约束破坏度记录的信息进行优化，扩大局部解的搜索范围，通过识别可行域空间进行种群的迭代。在完成迭代后，先对极端值进行调整，再逐次调整各时段变量使其符合约束，最终得到更高质量的解集。

3 实例研究

金溪是闽江上游的二级支流，位于北纬26°24′～27°07′，东经116°30′～117°56′之间，流域面积7 201 km2。流域开发的龙头电站——池潭水电站于1980年10月建成发电，控制流域面积4 766 km2，水库总库容8.7亿m3。池潭以下河段的梯级开发方案为良浅、大言、黄潭、孔头、范厝、高唐、谟武和贵岭水电站，共8级水电站。

本文设置灰狼种群个体数300，搜索最大代数2 000，以约束破坏度为主要目标，以发电量为副目标，收敛系数a计算公式为

表1 各电站最小生态流量 m3/s

(16)

式中，N为种群最大迭代次数。

最小生态流量按照福建省政府文件要求，取值为多年平均流量的15%，如表1所示。

为避免群智能算法计算的偶然性，分别使用遗传算法、粒子群算法、灰狼算法、改进灰狼算法进行10次计算，取平均值作为结果进行比较。评价指标包括约束破坏度、最大发电量及变化度。

约束破坏度随迭代次数下降趋势如图2所示。遗传算法和粒子群算法在600代左右就陷入了局部最优；灰狼算法和改进灰狼算法呈现局部波动、整体下降的趋势，在搜索后期依然具有优化效果，最终分别停止于30和10左右。在搜索的初期阶段，改进灰狼算法约束破坏度较高，这是由于在约束频繁破坏的初期增大了搜索范围；而在搜索的后期阶段，由于优化次数的减少，改进灰狼算法与灰狼算法的约束破坏度逐渐接近，但改进灰狼算法通过可行域的空间识别与迭代修正机制，约束破坏度下降更为明显。

图2 约束破坏度随迭代次数变化

表2所示为4种算法各进行十次计算所得最优个体的平均值。改进灰狼算法的最小约束破坏度降低至11.00；同时最大发电量优于其他算法，相比粒子群算法提升了10.76%，相比遗传算法提升了11.05%，大幅提升了电站效益。

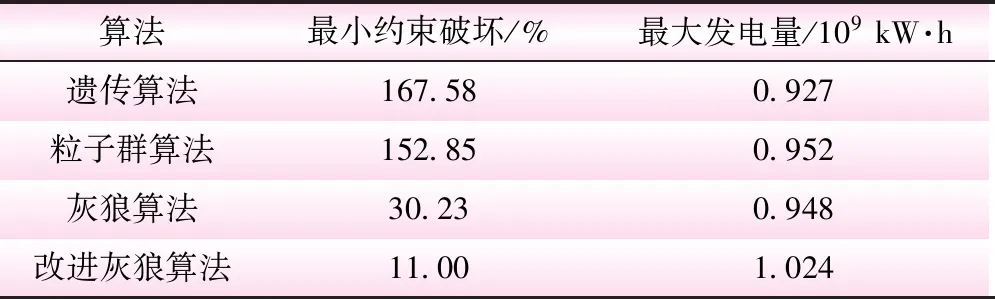
表2 算法评价指标

4 结 论

本文针对传统智能算法求解过程中的难以兼顾可行域搜索与目标跟踪能力的问题，基于灰狼算法的框架，结合“双适应度”排序方式，引入空间识别机制，用以驱动当前解趋近可行域空间并获得近似可行解。在此基础上，引入非可行域中近似可行解的迭代修正机制，进一步促进非可行解向可行解的过渡，得到收敛性、分布广泛性更好的解集。

通过对金溪流域的实例分析，与遗传算法、粒子群算法、灰狼算法相比，改进灰狼算法计算所得结果对约束破坏程度最小，解集收敛性能与目标优化的全局性能得到有效保障，发电效益显著提升，具备工程应用前景。