典型体型超高层建筑风振效应分析

叶风华

（1、广东省广建设计集团有限公司 广州 510500；2、广东建科施工图审查有限公司 广州 510010）

0 引言

随着城市高层建筑的集中化，建筑周围的风力变化更加复杂。风荷载已经成为了高层和超高层建筑结构设计的控制载荷，而建筑外形直接决定和影响着风荷载分布及其动力响应。目前，我国现行《建筑结构荷载规范：GB 50009—2012》［1］中仅给出了一些简单体型单体建筑的体型系数，而高层建筑风荷载的体型系数沿高度变化，且对于体型较为复杂的高层及超高层建筑，尚未有较明细的规定。相比美国ASCE/SEI 7-10［2］、日本AIJ-2004［3］、澳大利亚/新西兰AS/NZS 1170.2：2011［4］和 国 际 标 准 化 协 会ISO 4354：2002［5］等，关于高层建筑风荷载及其风致动力响应的计算方法与规定，仍有待进一步深化和完善。杨立国等人［6］结合5 栋超高层建筑群的风洞试验，研究了主体结构控制性风荷载及建筑顶层加速度的风荷载干扰效应；董欣等人［7］通过刚性模型风洞测压试验，研究了矩形截面高层建筑短边迎风和长边迎风时的表面风压特性及作用机理；庄翔等人［8］通过刚性模型风洞测压试验，对4 种不同的矩形截面圆角率进行了对比分析；ZUO 等人［9］对矩形结构进行了两阶段风荷载试验研究：第一阶段进行建筑全尺寸测量和缩尺模型的风洞试验，验证了风洞试验中使用的方法，第二阶段在风洞中测试了5 种不同体型的矩形结构模型；KIM 等人［10］通过研究指出通过改变结构体型来改变高层建筑周围的气流模式，从而减少风振；张夏萍等人［11］研究了高层金属网幕墙的抗风性能。本文结合两种体型、不同动力特性的代表性超高层建筑，对比研究不同规范计算得到的结构风荷载及其风致响应，同时将其与风洞试验结果展开对比调查，分析各规范在两类超高层建筑结构风荷载计算及其风致动力响应计算上的区别，以探讨文献［1］存在的优势与不足，为超高层建筑抗风设计和分析提供参考。

1 结构风致响应计算方法

高层结构在风荷载下的运动方程可表达为：

式中：φi（x，y，z）、φi（x＇，y＇，z＇）分别为第i振型对应于点（x，y，z）和点（x＇，y＇，z＇）的振型值；SP（n）为点（x，y，z）和点（x＇，y＇，z＇）的互谱密度函数。为体现基于风洞试验数据计算结构风致动力响应与现行规范的区别，结构承担的脉动风压的互谱密度函数采用非拟定常方法计算，并以此为基础计算结构的风致振动响应。非拟定常方法与现行文献［12］采用的拟定常方法相比，即可考虑风荷载的大气和结构湍流特征，又能兼顾场地环境对目标建筑物的干扰影响，尤其是结构横风向的涡激湍流作用效应。

现行文献［12］采用拟定常方法，式⑶可写为：

由此，根据随机振动理论可得结构风致位移响应的功率谱密度函数S（x，y，z，ω）：

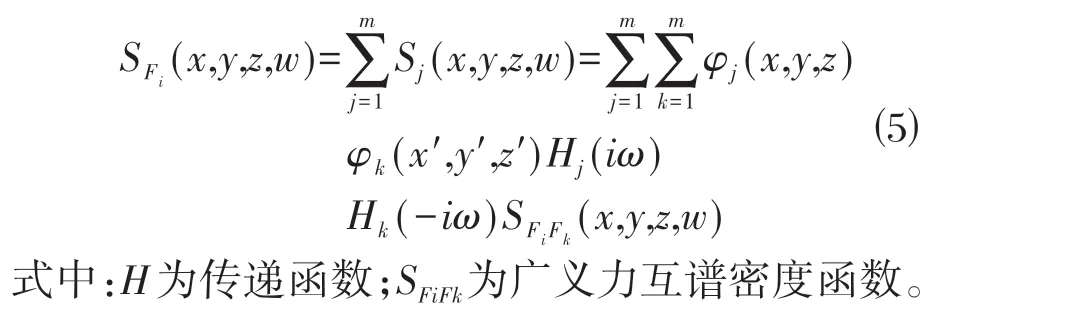
2 结构概况与动力特性

2.1 结构概况

模型A、模型B均位于广东沿海地区，为超高层风敏感建筑。模型A 由裙楼和塔楼组成，平面为正方形，但沿高度方向塔楼两侧截面不断内凹，而模型B平面为矩形，模型的结构参数及风洞试验参数如表1所示。风洞试验以正南方向为0°，风向角变化间隔为10°，测压风向角从0°到360°共36个工况。

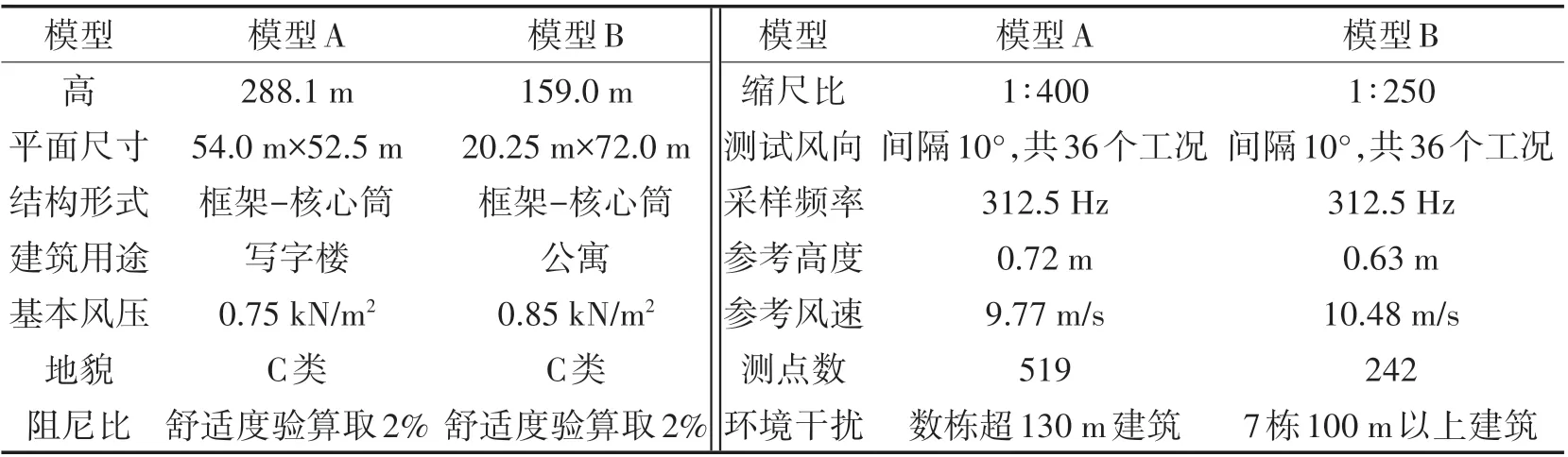
表1 两个模型结构参数与风洞试验参数汇总Tab.1 Summary of Structural Parameters and Wind Tunnel Test Data of the Two Models

2.2 动力特性

模型A 和模型B 的动力特性如表2 所示。模型A第一、二振型以平动为主（振型质量参与系数均为61%），第三振型为扭转（振型质量参与系数53%）；扭转与平动第一周期比值0.74，满足《高层建筑混凝土结构设计规程：JGJ 3—2019》［13］B 级高度不大于0.85的要求，且前两阶周期分别为6.832 s 和6.565 s，相差较小，说明模型A扭转效应小。

表2 结构前6阶动力特性Tab.2 First Six Orders of Dynamic Characteristics of the Two Models

模型B 第一振型为平动（振型参与系数100%），第二、三振型均为扭转与平动耦合振型，其中第二振型平动、扭转参与系数分别为36%、64%，第三振型平动、扭转参与系数分别为64%、36%；扭转与平动第一周期比0.844，虽满足设计要求，但接近限值，模型B扭转效应大。

3 结果分析

3.1 结构风荷载

模型A 和模型B 沿高度方向风荷载基于规范和风洞试验的计算结果对比如图1 所示。基于文献［1］的结构顺风向风荷载计算结果均随楼层高度呈现不断增大的趋势，除基于文献［5］模型A 的上部楼层、基于文献［4］模型B 的下部楼层的风荷载较大外，两种模型在不同方向角风荷载作用下文献［1］关于结构顺风向风荷载的计算结果均较大，如模型A 在0°风向角条件下，顶层顺风向基于文献［1］得到的风荷载是相同风向下基于风洞试验结果的1.87倍。

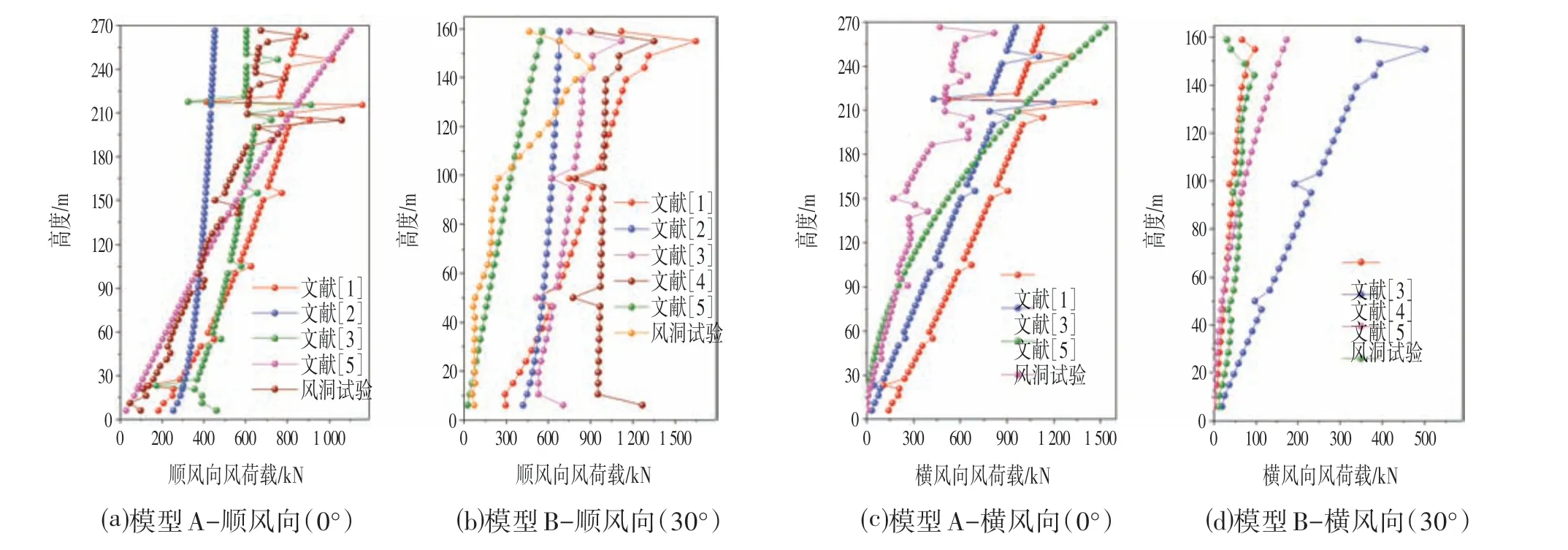
图1 沿高度方向结构风荷载基于规范和风洞试验的计算结果对比Fig.1 Results Comparison of Structural Wind Load along Height Based on Codes and Wind Tunnel Tests

对于模型A 的横风向风荷载，基于文献［1］的计算结果与模型A顺风向风荷载类似，即除基于文献［5］上部楼层的风荷载较大外，文献［1］计算结果均高于文献［2-5］及风洞试验结果。对于模型B，文献［1］没有对应的计算方法，通过文献［3］、文献［4］和文献［5］与风洞试验结果的对比来看，基于风洞试验的横风向风荷载与文献［3］比较接近，文献［5］计算结果偏大，文献［4］计算结果远高于前者，主要原因在于文献［4］计算此类结构横风向风荷载时的风振因子和背景因子取值很大而导致。

在文献［1］给出的计算公式的适用范围内，结合C类地貌两种不同体型超高层建筑风荷载的计算结果，可以看出基于文献［1］顺风向、横风向风荷载的计算结果较为保守，偏于安全。为说明周围环境干扰对双轴对称建筑物风荷载分布的影响，图2 给出了基于风洞试验的模型A 的顺风向、横风向风荷载沿高度的分布情况，其中0°-180°、90°-270°均为反向的风向角输入。由图2可见，对于双轴对称的模型A，由于受到周围建筑物的干扰效应，对称方向结构顺风向和横风向的风荷载沿高度方向均存在一定的差异，模型A 在0°～180°风向角输入下其顺风向和横风向风荷载最大差异百分比分别为44.0%（第1 层）、97.5%（第2 层），在90°～270°风向角输入下相应的差异分别为49.9%（第1层）、40.38%（第45 层），其沿楼层高度方向的平均差异百分比依次为22.99%、27.06%、31.16%和24.4%。可见，结构风荷载计算应充分考虑周围建筑物的干扰效应，保证输入风荷载的可靠性。

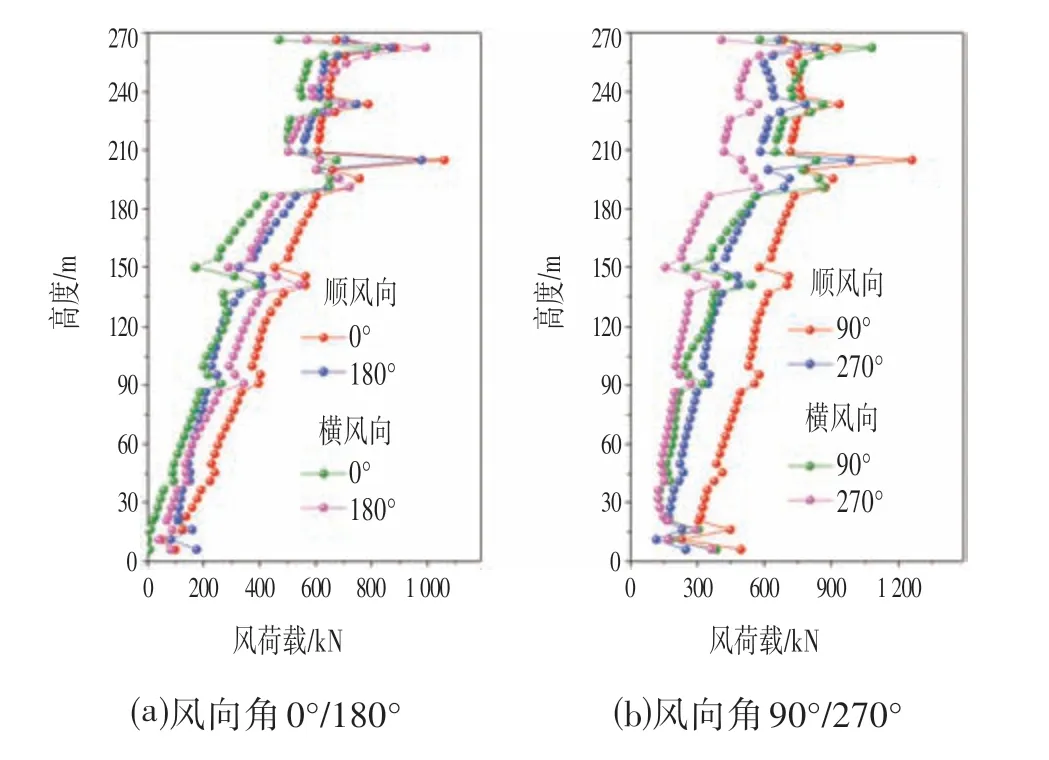
图2 基于风洞试验的模型A风荷载计算对比Fig.2 Wind Load Comparison of Model A with the Test

3.2 结构基底剪力与基底弯矩

基于风洞试验的两个模型基底剪力和弯矩随风向角的变化曲线如图3 所示。可见，不同风向角风荷载输入下结构基底剪力和弯矩存在较大的波动，对于方形建筑模型A 基底弯矩最大值较最小值分别高2.12 倍（Mx）和2.74 倍（My）、基底剪力最大值较最小值分别高2.9 倍（Fx）和2.3 倍（Fy）。然而，对于模型B，基底弯矩最大值较最小值高7.09 倍（Mx）和6.29 倍（My）、基底剪力最大值亦达到最小值的7 倍（Fx）和7.33 倍（Fy）。说明体型规则且双向抗侧刚度均匀的高层建筑，其在不同风向角风荷载作用下的结构受力特征更加有利，有利于避免受力波动过大的现象。

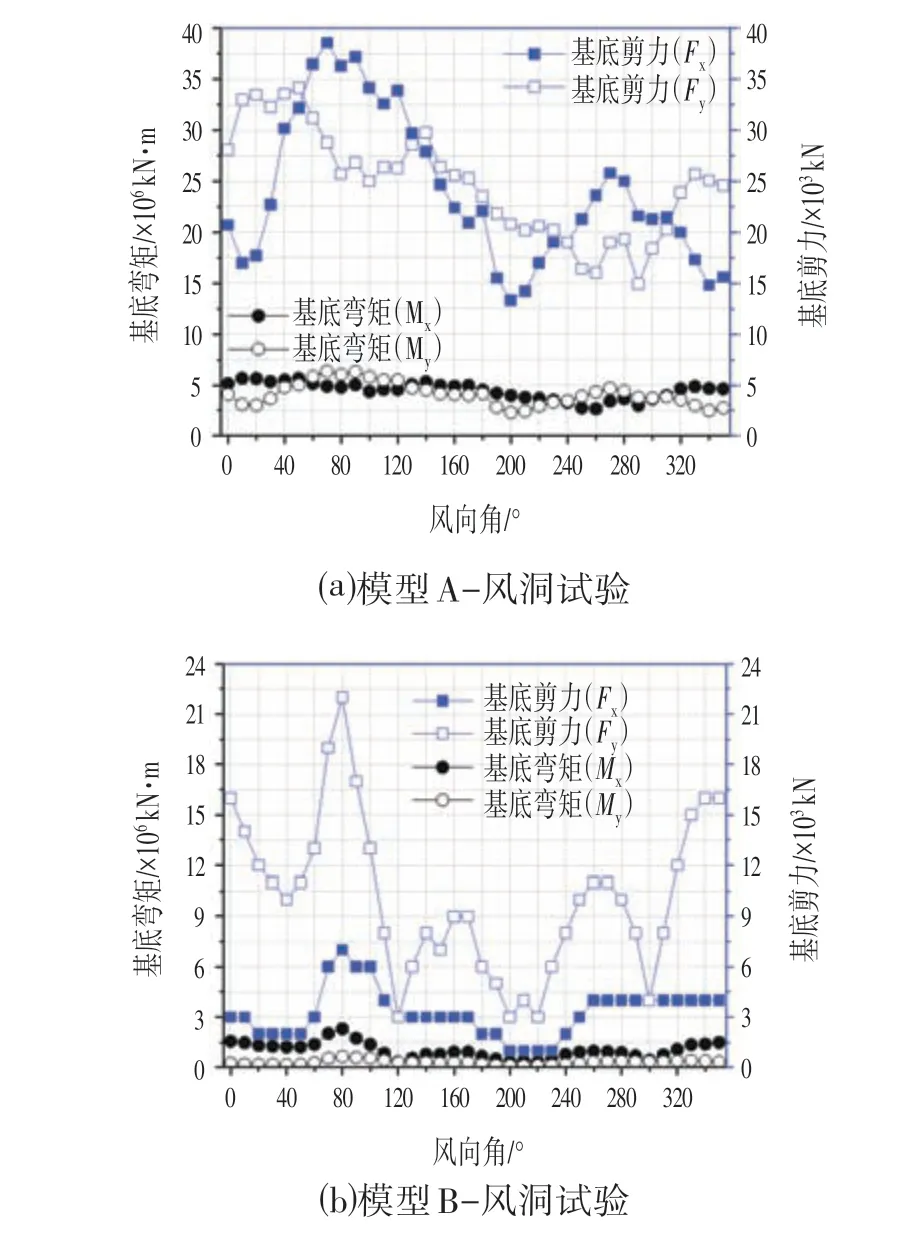
图3 结构基底剪力与基底弯矩随风向角变化曲线Fig.3 Variation Curves of Structural Base Shear Force and Base Bending Moment with Wind Angles

各国规范基于简化计算方法只能开展正交风向角下结构风振效应计算，为便于对比，将与结构坐标轴对应的正交风向角下，基于风洞试验和各国规范计算得到的基底弯矩响应进行对比，如图4 所示。不论是不同动力特性的两种模型还是顺风向、横风向作用，基于文献［1］得到的基底弯矩均较大。对于模型A，顺风向和横风向下的基底弯矩与文献［5］接近，高于对应风向角作用下其他规范和风洞试验结果；对于模型B，顺风向作用下的基底弯矩与文献［4］接近，并同样高于对应风向角作用下其他规范和风洞试验结果。说明文献［1］对于超高层结构基底内力的计算结果同样具有较高的安全裕度，偏于安全设计。然而，即便从图4 中看出风洞试验结果普遍偏小，低于各国规范计算值，但这并不意味规范设计过于保守，相反，基于图3基底剪力/弯矩随风向角的变化曲线，实际上结构基底剪力/弯矩并不出现在与结构坐标轴对应的正交风向角下，基于规范设计考虑充分的安全裕度是非常必要的。

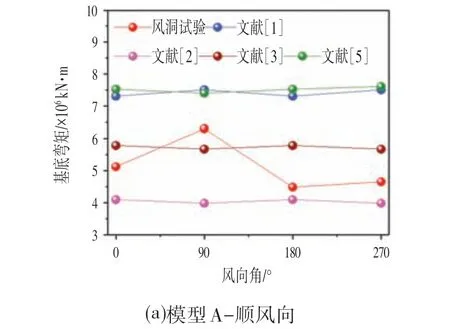
图4 典型风向角下基于风洞试验和规范的结构基底弯矩对比Fig.4 Comparison of the Base Bending Moment Based on Wind Tests and Codes under Typical Wind Angles

3.3 建筑顶点舒适度

基于风洞试验和不同规范的两类体型超高层建筑的顶点顺风向、横风向加速度响应见表3 和表4。对于模型A，顺风向顶点加速度采用文献［1］、文献［3］的计算结果较接近，但都低于风洞试验，后者较文献［1］分别高31%（0°）、43%（90°）、25%（180°）和37%（270°）；文献［2］顺风向顶点加速度计算结果最高，其原因在于采用风速平方函数计算顺风向风振响应，比文献［1］和文献［3］的设计计算风速大，顺风向顶点加速度计算结果约为模型A基于文献［1］的3倍；横风向顶点加速度采用文献［1］的结果与风动试验相比，平均差异17.8%；基于文献［3］横风向顶点加速度计算结果最大，4个风向角下文献［3］较文献［1］平均高47%、较风洞试验平均高41.2%。与风洞试验结果及文献［3］相比，文献［1］顶点顺风向和横风向加速度在一定程度上能反映结构舒适度，但计算结果偏低，尤其是对结构舒适度起控制作用的横风向，宜进一步完善，考虑更多的耦合因素，如高阶振型、周围环境干扰效应等。

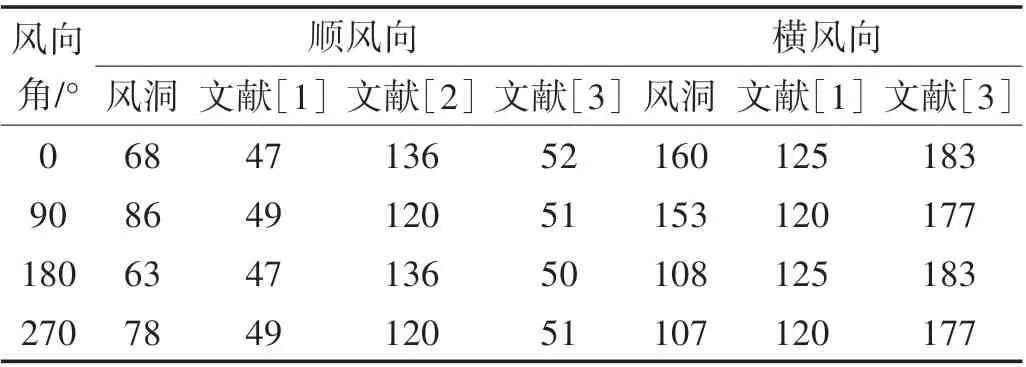
表3 模型A顶点加速度Tab.3 Top Accelerations of the Model A （mm/s2）

表4 模型B顶点加速度Tab.4 Top Accelerations of the Model B（mm/s2）

对于模型B，在4 个风向角下顺风向顶点加速度的计算结果文献［1］虽然高于风洞试验结果，但仍低于文献［3］、且远小于文献［2］、文献［4］。文献［1］、文献［2］、文献［4］目前还没有长宽比较大的结构横风向加速度计算公式，文献［3］虽给出，但结果与风洞试验存在很大差异，如4个风向角下文献［3］与风洞试验横风向顶点加速度差异分别为70.37%（30°）、39.34%（120°）、206.67%（210°）和28.79%（300°）。因此，建议基于风洞试验确定结构横风向风振加速度，亟待发展精确有效且适用广泛的超高层横风向加速度公式。

4 结论

基于风洞试验和国内外规范，研究了两种体型超高层建筑结构的风致振动效应，结论如下：

⑴随楼层高度增大，基于文献［1］的结构顺风向和横风向风荷载亦呈现不断增大的趋势，采用文献［1］计算的方形平面体型建筑顺风向、横风向风荷载以及矩形体型建筑顺风向风荷载均较风洞试验和其他规范大，计算结果偏于安全。

⑵周围环境对目标建筑物的干扰效应显著，对称结构在对称风向角风荷载输入下，结构顺风向和横风向风荷载存在较大的差异，计算时应予以充分考虑，如模型A沿高度方向最大差异达97.5%、平均差异达31.16%。

⑶文献［1］对于超高层结构基底内力的计算结果具有较高的安全裕度，偏于安全设计。体型规则且双向抗侧刚度均匀的高层建筑，在不同风向角风荷载下的结构受力特征更加有利，基底反力最大值与最小值的差距相对较小。

⑷与风洞试验及文献［3］相比，文献［1］对于双向抗侧刚度较为均匀的建筑，顶点顺风向和横风向加速度在一定程度上能反映结构舒适度，但结果偏低，尤其是对结构舒适度起控制作用的横风向。建议针对有效的且适用范围广的超高层横风向加速度计算公式开展深入探讨。