基于BPSK-CSK的电文调制与解调算法

王环宇，袁木子，马春江，唐小妹，欧钢，林红磊

(国防科技大学 电子科学学院,长沙 410073)

0 引 言

随着无人驾驶[1]、精密农业[2]等精细化行业的发展，用户对精密定位服务的需求提高，而实现精密定位服务需要导航信号传输大量校准参数等信息，对导航信号的信息传输速率提出了更高要求.传统的二进制相移键控(BPSK)若想达到提高信息速率的目的，需要提高码率从而导致更宽的频谱，或降低一个码周期的码片数而导致扩频码隔离度和正交特性的损失.由于BPSK 的局限性以及应用需求，业内专家提出采用码移键控(CSK)进行电文符号调制[3-4]，该方法在提高信息传输速率的同时，有效避地免了BPSK 的局限性，但同时由于CSK 采用不同相位的伪码序列调制信息，通过多个相关器对采样信号进行匹配操作，引入了占用更多相关器资源和高计算复杂度的问题[5].针对这一问题，CHAUVAT 等[6]提出在解调之前使用数字芯片匹配滤波降低单位符号内的采样点数，从而降低CSK解调计算复杂度；王盾等提出双极性码移键控(BCSK)将解调的计算复杂度降低3 dB[7-8].

CSK 通过伪随机序列码相位的不同调制信息，接收端需要与码相位个数相等的相关器组，对大量信号采样值进行运算操作，完成解调，导致计算复杂度高的问题.二进制相移键控-码移键控(BPSK-CSK)联合调制方法是对BCSK 的发展，通过改变信号调制的结构，在传统CSK 的基础上调制子码，使接收端由原本单纯使用相关器对采样信号进行CSK 解调，转变为分两步解调电文，即第一步由相关器对采样信号进行操作，第二步对第一步所得的相关值进行操作.相比于传统的CSK 解调，BPSK-CSK 相干解调所需相关器个数减少，减少的相关器对采样信号的运算操作次数由对数量级远小于信号采样的相关值进行运算替代，从而降低接收机的计算复杂度.

后文详细介绍BPSK-CSK 调制方法以及相干解调流程，对解调算法进行误比特率理论分析以及仿真验证，之后分析BPSK-CSK 相干解调的计算复杂度，并结合信道编码进一步分析BPSK-CSK 的应用优势.

1 电文调制

1.1 CSK 调制

CSK 是一种直接序列扩频方法，利用伪随机码的自相关性能，即同一组伪随机码的不同码相位之间正交的特点.该方法设置一组基础伪随机码，通过循环移位得到M组不同码相位的伪随机码，连续N个相同相位的伪随机码表示1 个CSK 符号，该符号调制U=log2(M) 比特信息，记为CSK(U,N).CSK 的基础码记为cd(t)，通过循环移位生成的M个CSK 符号表示为ci(t)，其中i=0,···,M-1，循环移位的数学表达式为

式中：mi为第i个符号的码移位位数；Tc为码片持续时长；lb为基础码码长，该值不一定等于M；mod(x,y)表示y对x的模运算.以N=1，U=2 bits 为例，CSK 符号生成以及电文比特调制的示例如图1所示[9].

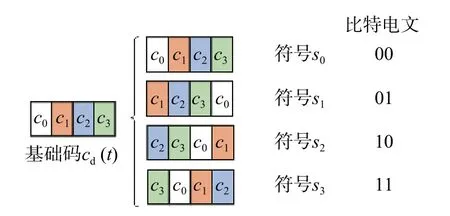
图1 CSK(2,1)符号生成示意图

1.2 BPSK-CSK 调制

本文针对传统CSK 解调计算复杂度高的问题提出BPSK-CSK 调制算法，采用主码与子码的双层调制结构，将CSK 符号作为主码，在主码上根据电文极性位调制拓展的子码得到一组码序列，N个连续的码序列表示1 个BPSK-CSK 符号，记为BPSK-CSK(U,K,N).其中U表示1 个BPSK-CSK 符号调制U比特电文，U比特电文由Kbits 极性位和(U-K) bits 码相位组成，将BPSK-CSK 的基础码记为cd(t)，通过循环移位生成Mprime=2U-K个BPSK-CSK 主码，这一过程与CSK 符号生成过程相同，之后在主码上调制子码，共Msub=2K种子码，最终可以得到M=2U种码序列，将得到的码序列重复N次可得到M种BPSK-CSK符号，符号生成过程如图2所示.

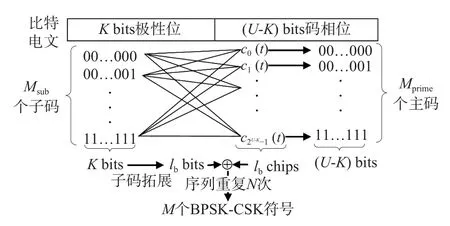
图2 BPSK-CSK 符号生成示意图

图2中lb表示基础码码长，该值为K的整数倍，子码拓展是指将Kbits 子码的每一比特重复lb/K次的过程，从而得到长度为lb的拓展子码.当信息速率为Rb，基础码码率为Rc时，一个BPSK-CSK 符号的持续时长，即接收端进行U比特电文解调的相干时长为Tcoh，表示为

则U与Tcoh的关系为

以BPSK-CSK(4,2,2)为例，为简化说明过程省略信号采样.设lb=8 bits，Rc=16 000 码片每秒(chips/s)，Rb=4 Kbps基础码，以 (1,0,0,1,0,1,1,0) 为例，则M=16，子码Msub=22=4，主码Mprime=22=4，全部BPSKCSK 符号生成过程如下：

1) 表1将基础码通过循环移位生成4 个主码；

表1 BPSK-CSK(4,2,2)主码列表

2) 表2将4 bits 电文中极性位进行子码拓展；

表2 BPSK-CSK(4,2,2)拓展子码的生成

3) 表3将主码与拓展子码按位异或得到码序列，并将该序列重复2 次得到所有BPSK-CSK 符号.

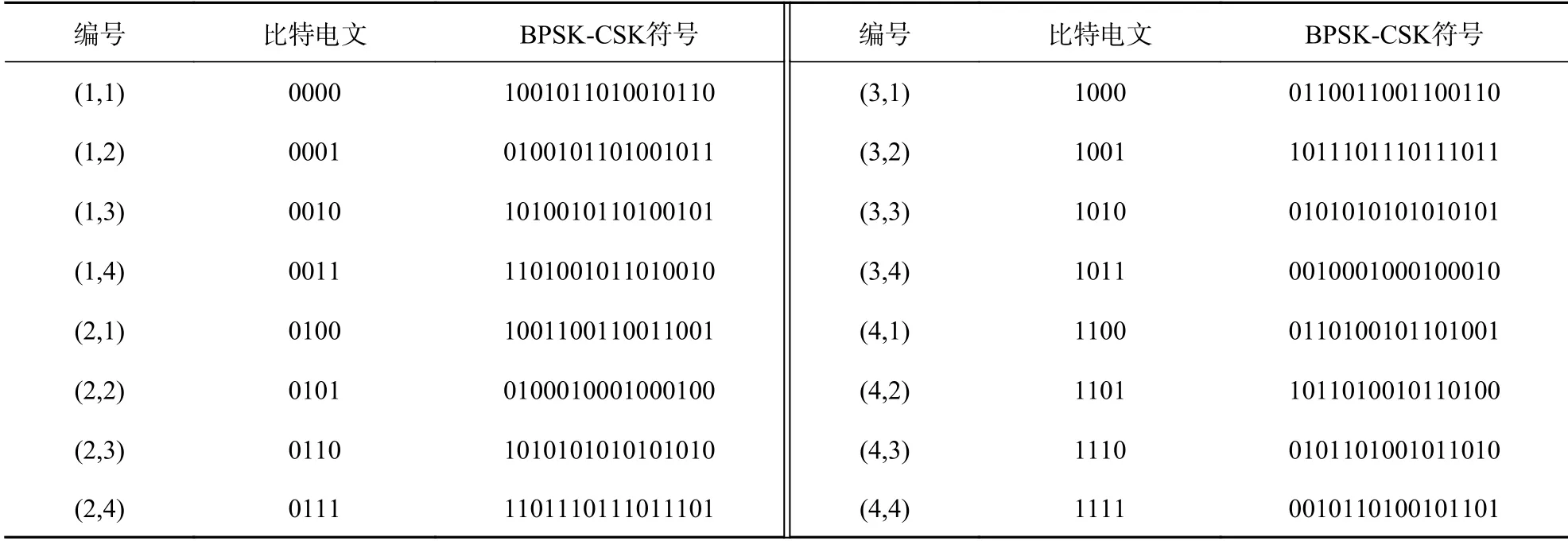
表3 BPSK-CSK(4,2,2)符号列表

2 电文相干解调

接收端对信号进行下变频混频和模数转换后得到的信号时域数学模型为

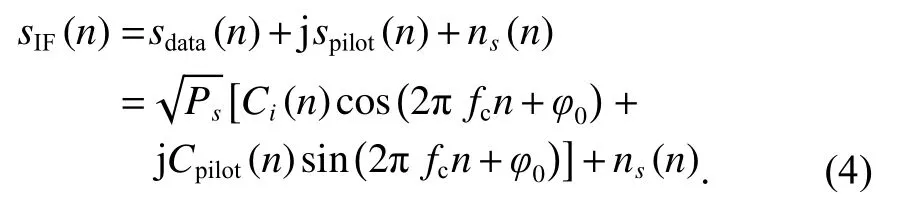
本文假设接收信号由导频分量spilot(n) 和数据分量sdata(n) 组成，两分量相互正交，数据分量采用BPSK-CSK 或CSK 方法进行电文调制.Ci(n) 为第i个CSK 或BPSK-CSK 符号，该符号的选择在电文调制时，由分组后的各组电文决定.导频分量采用BPSK，不调制电文，只用于导航信号的捕获与跟踪.Cpilot(n)为导频分量的扩频码，其中Ps为信号功率；fc为载波中频频率；φ0为初始载波相位；ns(n) 为高斯白噪声；信号载噪比N0为噪声功率频谱密度.

接收机利用spilot(n) 进行导航信号的捕获与跟踪，之后载波数字振荡器(NCO)根据跟踪得到的载波相位和载波频率生成正弦波和余弦波对数据分量进行载波剥离得到

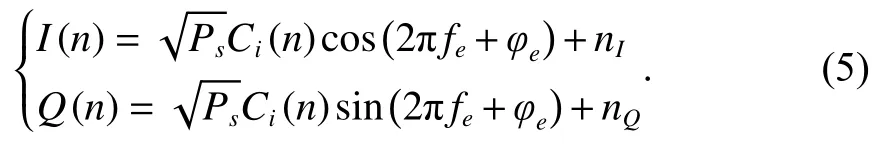
式中，i=0,···,M-1.

假设接收机导频段准确捕获与跟踪，即接收载波频率与搜索载波频率之间的差异fe≈0，两载波之间的相位差异φe≈0，则I(n)和Q(n) 可以化简为

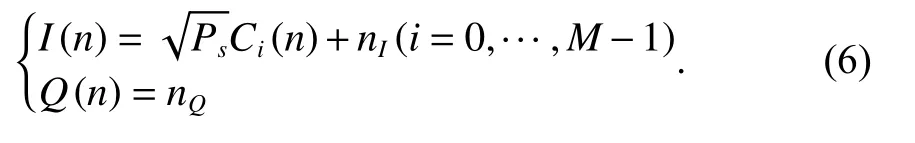
式(4)中，nI和nQ为在同相支路I支路和正交支路Q支路上均值为零且互不相关的正态噪声.在完成载波剥离后进行电文相干解调，正交支路不计入判决.

2.1 CSK 相干解调

如图3所示，电文解调模块根据跟踪阶段所得码相位的值定位CSK 电文调制部分的起始点，设向量r表示I(n) 在起始点对齐后1 个CSK 符号周期内的信号采样向量，ci(i=0,···,M-1) 为本地生成的M个CSK 符号向量.传统CSK 解调模块采用M个相关器进行CSK 符号匹配，通过相关求和，得到判决向量R，Ri(i=0,···,M-1) 为R中的元素，R中最大元素对应的CSK 符号及该符号对应的电文为电文解调结果.

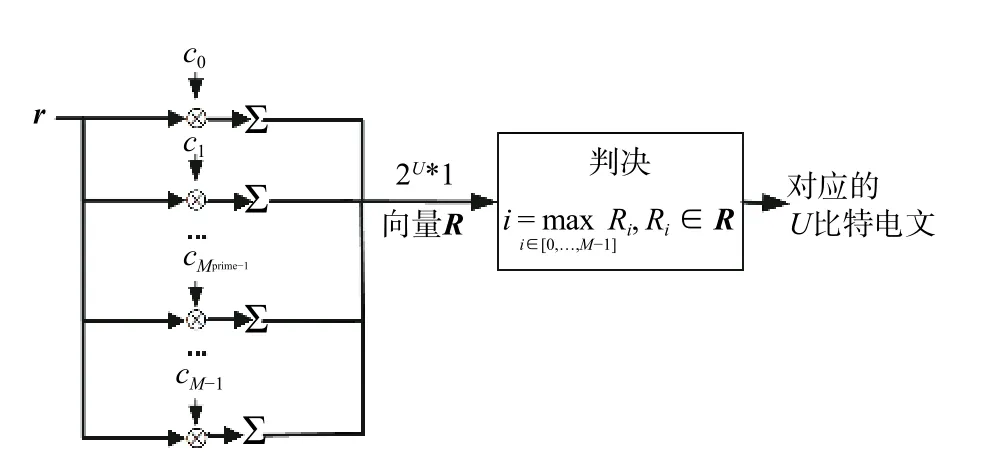
图3 CSK 解调模块

2.2 BPSK-CSK 相干解调

与CSK 解调模块类似，BPSK-CSK 电文解调模块依赖于跟踪结果得到BPSK-CSK 符号起始点.如图4所示，设向量r为I(n) 在起始点对齐后1 个BPSK-CSK 符号周期内的采样向量，并将r平均分为NK段得到行向量rs1到rsNK，NK分段之间相互独立，接收机本地将Mprime个主码分别分为NK段，得到行向量sj,1到sj,NK(j=0,···,Mprime-1)，将r与不同主码的各分段分别进行相关求和运算，将每个主码对应的NK个求和结果以K个求和结果为单位分为N组，每组对应位置相加求和，最终得到维度为Mprime×K的相干矩阵Rprime，表示为

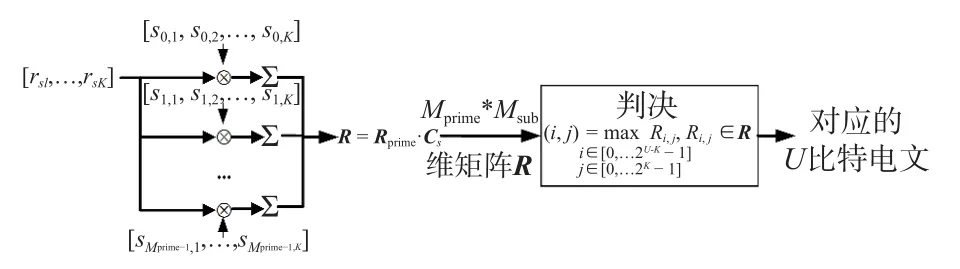
图4 BPSK-CSK 解调模块

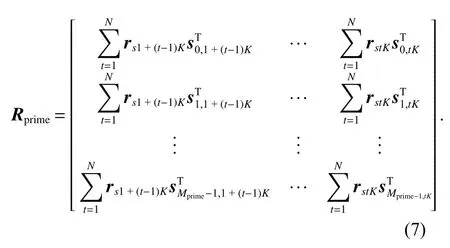
进行相关求和后，由于rs1到rsNK长度相等，Rprime中各随机变量噪声功率(即方差) σ2n相等，表示为

Tcoh表示一个BPSK-CSK 符号持续时长即相干时长，由式(8)可知，Tcoh越大相干矩阵中各随机变量的噪声功率越小，信号功率保持不变时，信噪比越大.

将相干矩阵Rprime与维度为K×Msub子码矩阵Cs相乘求得维度为Mprime×Msub的判决矩阵R，求得该矩阵的表达式为

判决矩阵R的第i行对应第i个BPSK-CSK 主码，第j列对应第j个BPSK-CSK 的子码，则判决矩阵R的元素Ri,j为r与该主码和子码对应的BPSKCSK 符号的相关值，则R中最大值对应的BPSKCSK 符号对应的U比特电文为解调结果，该过程表示为

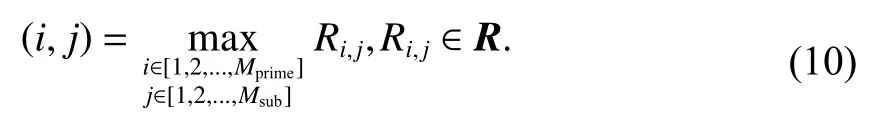
对比图3～4 可知，与传统CSK 解调模块相比，BPSK-CSK 解调算法所需相关器个数减少了(MMprime)个，并使用矩阵乘法替代这部分对采样信号的运算操作.分步进行的相干解调是由BPSK-CSK 调制结构决定的，是降低计算复杂度的关键.

3 性能分析

3.1 相干解调算法的误比特率

判决矩阵R中包含M=Mprime×Msub个元素，通过检测最大相关值对应的主码和子码编号确定比特电文.检测统计量为Ri,j，由于同一主码对应的子码匹配过程是针对同一组相关值进行的，因此判决矩阵R中同一行内的Msub个元素相互不独立，由于BPSK-CSK主码的生成与CSK 一致，不同主码对应的行之间相互独立.在误比特性能的分析过程中，依据是否与BPSK-CSK 主码匹配将矩阵R分为两部分，下文中分别称为主码匹配行和未匹配行，分别计算误比特率.

对于未匹配行，假设BPSK-CSK 主码为性能理想的随机码，相互正交，不考虑互相关干扰，即各分段都服从均值为0，方差为 σ2n/2 的高斯分布，概率密度表示为g(x)，分布函数表示为G(x)，基于这一假设，可知未匹配行的 (M-Msub) 个元素被判为最大值的概率相等.

则主码匹配行中，与子码匹配kbits 的元素有k分段服从(K-k)分段服从σ2n/2)，由于同一行的相关值相互不独立，当且仅当每一分段的相关值取值大于0 时，对应的相关值被判为该行的最大值，此时各分段服从截断高斯分布，f1(x)和f2(x) 的截断高斯分布的概率密度函数分别表示为

Ri,j表示K段相关值与编号为j的子码相乘后求和的结果，这K个随机变量相互独立，因此主码匹配行中，将与子码匹配kbits 的元素判定为主码匹配行的最大值，这种情况的概率密度表示为

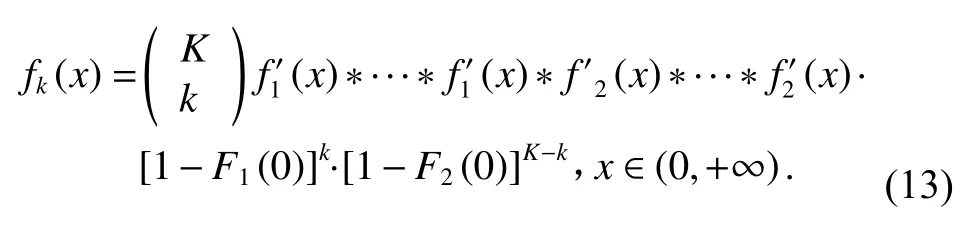
式中：k个f1′(x)；(K-k)个f2′(x)；*表示卷积运算；两个相互独立的变量X和Y，概率密度函数分别表示为fX(x)和fY(x)，则变量Z=X+Y的概率密度函数fZ(z)表示为

同理，非匹配行中最大值元素的概率密度函数gmax(x)的表达式为

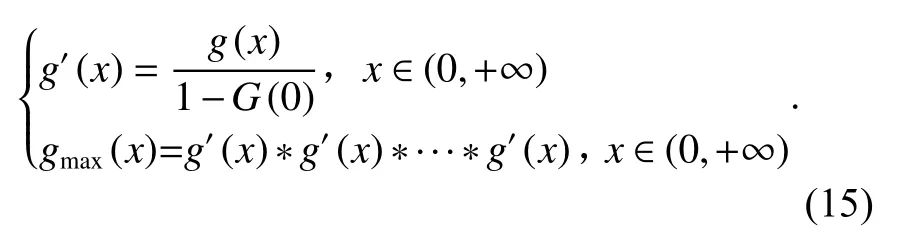
则主码匹配成功的概率为

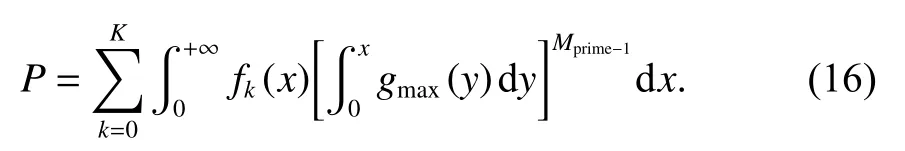
非匹配行的误比特率表示为

主码匹配行的误比特率表示为

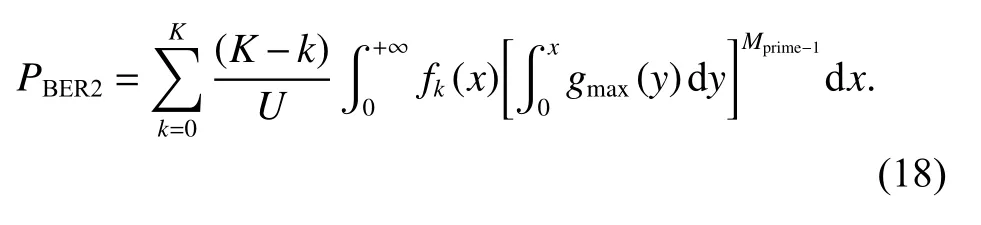
因此，信号载噪比为RCN0时，BPSK-CSK(U,K,N)电文解调的误比特率表示为

值得注意的是，当K=0 时，BPSK-CSK 调制与CSK 调制等价，误比特率的表达式为[10]

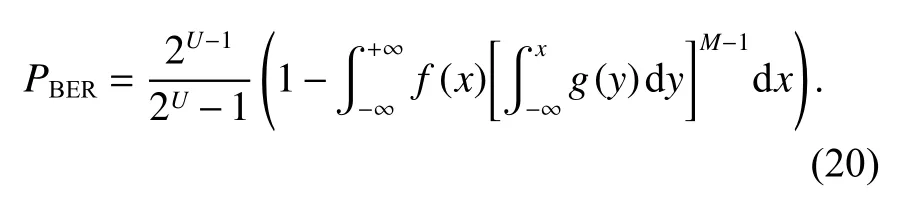
式中，f(x) 表示均值为0，方差为 σ2=的高斯分布.

当K=U时，BPSK-CSK 调制与BPSK 调制等价，误比特率的表达式为[11]

式中，Q(·) 表示标准正态分布的右尾函数.

为验证理论推导的正确性，本文进行了BPSKCSK 相干解调仿真.本仿真在信号生成阶段，随机生成相应长度的扩频码，信息层随机生成电文比特，不进行信道编码，设码率为Rc=2.046 MHz，电文速率为Rb=1 Kbps，进行BPSK-CSK(U,K,1)电文调制，根据式(4)生成不同载噪比条件下的卫星导航信号；在信号接收阶段，假设低动态卫星导航接收机准确跟踪信号，具备电文相干解调条件，以U比特电文为一个单位，进行106次蒙特卡洛仿真，得到误比特率的仿真结果.

仿真以BPSK-CSK(6,4,1)为例，根据式(3)可得1 个BPSK-CSK 符号时长为Tcoh=6 ms，仿真过程中信号载噪比不变，单个BPSK-CSK 符号时长Tcoh决定了电文解调的相干累加时长，从而导致信噪比的变化，相干累加时长越长，用于电文解调的信号信噪比越大.图5是该调制方法误比特性能的仿真与理论曲线图，由图5可知，误比特性能的仿真结果与理论分析一致.

图5 BPSK-CSK(6,4,1)在1 Kbps 电文速率下的仿真与理论曲线图

图6是在相同电文速率Rb=1 Kbps 条件下，当K∈{0,1,2,3,4,5,6}时，BPSK-CSK(6,K,1)在不同信噪比条件下的误比特性能曲线图，经计算CSK(6,1)的误比特率与BPSK-CSK(6,0,1)相等，BPSK 误比特率与BPSK-CSK(6,6,1)相等，因此图中K=0 bits 和K=6 bits 的曲线直接标注为CSK(6,1)和BPSK.

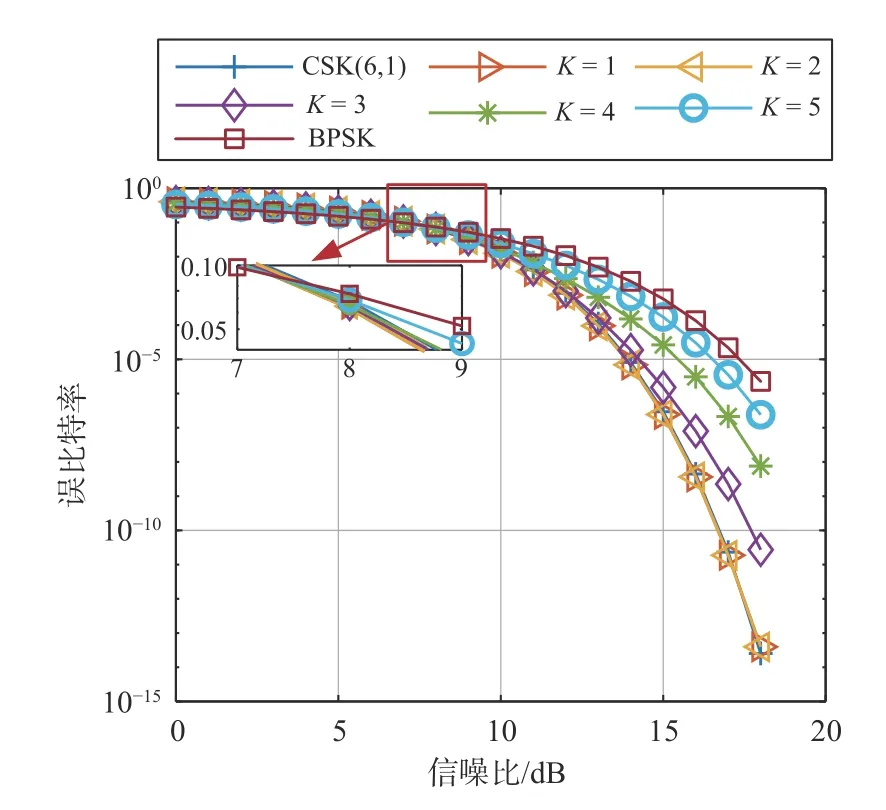
图6 当K∈{0,1,2,3,4,5,6}时BPSK-CSK(6,K,1)在不同信噪比条件下的误比特率曲线

由图6可得到以下结论：

1) 当K∈{0,1,2} 时，BPSK-CSK(6,K,1)调制的误比特性能基本保持不变，与CSK(6,1)的误比特性能相等.

2) 当K＞2 时，BPSK-CSK 的误比特性能位于BPSK 和CSK 之间，随着K的增大，误比特曲线更靠近BPSK，电文解调门限逐渐增大.

3) 高信噪比是CSK 相对于BPSK 降低电文解调门限的前提.如图6所示，曲线交点约为7.7 dB，当信噪比低于7.7 dB 时，BPSK 调制的误比特性能更好，此时，将低于7.7 dB 的信号视为低信噪比信号，使用BPSK 调制更有优势.需要注意的是，这里的低信噪比是相对于图中曲线交点而言.

3.2 计算复杂度

本节对BPSK-CSK(U,K,1)和CSK(U,1)的相干解调算法的计算复杂度进行分析，由于接收机使用相关器组通过相关求和的方法进行电文解调，两种解调方法的计算复杂度量级是相等的，因此通过详细对比乘法操作的次数分析BPSK-CSK 相较于CSK 计算复杂度的降低程度.

在相等电文信息速率、相等扩频码码率、码周期以及采样频率的条件下，CSK 和BPSK-CSK 以1 个符号为单位进行电文符号解调，设1 个CSK 符号或BPSK-CSK 符号持续时间相等且采样点数为L，则CSK 解调每个符号进行的乘法运算次数O1表示为

BPSK-CSK(U,K,1)解调每个符号进行的乘法运算次数O2表示为

则对于单个符号相干解调的计算复杂度，BPSKCSK 的计算复杂度与CSK 计算复杂度的比表示为

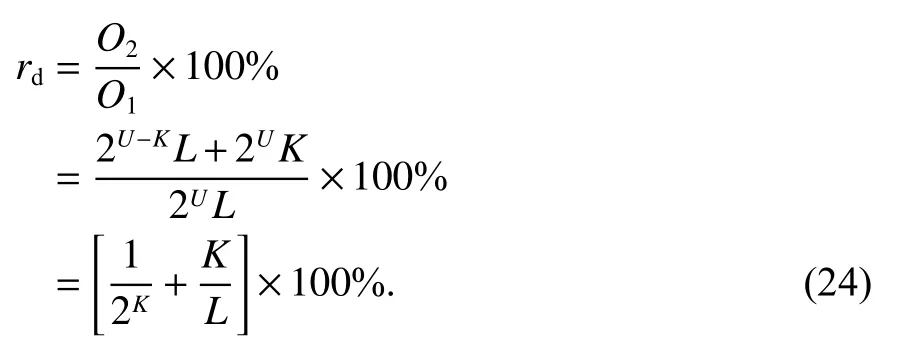
由式(24)可知，BPSK-CSK(U,K,1)相干解调计算复杂度和CSK(U,1)计算复杂度的比值与1 个符号携带的电文比特数U无关，而与极性位比特数K有关.如图7所示，假设U足够大，随着K值的增大，BPSK-CSK 对CSK的计算复杂度削弱程度先呈指数上升，削弱程度到最大时呈线性缓慢下降，当K约为13 时，BPSK-CSK 相对于同等量级CSK 的计算复杂度削减程度最高.

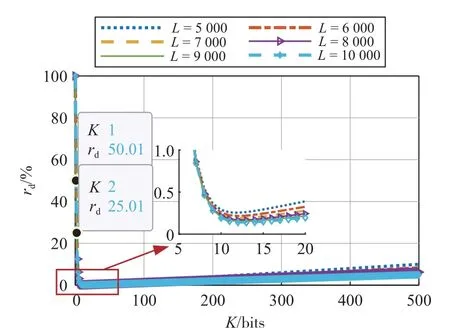
图7 BPSK-CSK(U,K,1)与CSK(U,1)相干解调乘法运算次数比曲线图

此外，当K值不变时，1 个符号内采样点数L越大，BPSK-CSK 对于同等量级CSK 的计算复杂度削减程度越高.

3.3 应用示例

上文对误比特性能与计算复杂度的分析未考虑纠错编码，在K＞2 时，BPSK-CSK 以误比特性能为代价换取计算复杂度的降低，本节针对这种情况列举一种BPSK-CSK 的应用示例.假设BPSK-CSK 调制的电文符号经过纠错编码，接收端在相干解调后需进行信道译码，权衡译码引入的计算复杂度和编码增益(编码增益指给定输出误码率下编码与非编码序列输入信噪比的差值)，与相等计算复杂度的CSK 对比误比特性能.

根据文献[12]对信道编码的研究以及上文的理论分析，当系统的误码指标为10-5且接收端采用硬判决译码时，BCH(15,7)纠错编码的编码增益约为4 dB.

BCH(15,7)纠错编码将电文以7 bits 为单位分组，纠错编码之后得到码长为15 bits 的码字，因此电文调制过程以15 bits 为单位采用BPSK-CSK(15,3,1)算法.设信息速率为Rb=1 Kbps，码率为Rc=2.046 MHz，采样频率取5 MHz，根据式(3)求得此时BPSK-CSK符号持续时长为15 ms，则有效信息速率约为467 bps.根据式(22)～(23)，求得CSK(12,1)在上述条件下与BPSK-CSK(15,3,1)解调等量的有效信息所需计算复杂度近似相等，此时一个CSK(12,1)符号持续时长约为25 ms.根据式(19)～(20)，在未进行纠错编码时，BPSK-CSK(15,3,1)的电文解调门限约为16.95 dB，CSK(12,1)的电文解调门限约为15.05 dB.由于BCH硬判决译码的计算复杂度远小于电文符号解调的计算复杂度，对接收机整体的计算复杂度影响较小，因此在计算复杂度近似相等、有效信息速率近似相等的条件下，编码后的BPSK-CSK(15,3,1)解调门限为12.95 dB，低于CSK(12,1)的解调门限2.1 dB.

当接收端解调相等的有效信息时，假设计算复杂度相等(O1=O2)、有效信息速率相等、信号采样率与码率相等，计算可得BPSK-CSK(U,K,N)对应的CSK调制参数，可知BPSK-CSK 调制信号的总信息速率更高，即该方法在相等的传输时间内传输的信息量更大，除有效信息外可用于纠错编码的冗余比特数更多.存在一种纠错编码方法，其编码增益随冗余纠错码位数的增多而提高，从而有效弥补了K＞2 时BPSKCSK 相对于CSK 误比特性能的损失，甚至提高误比特性能.本节分析了一种极端情况，即BPSK-CSK 采用纠错编码而CSK 未采用纠错编码，验证了上述情况下本文所提方法的优势.需要注意的是，对于不同的信道编码方法，需要权衡信道译码引入的计算量与带来的编码增益.

4 结 论

针对CSK 解调计算复杂度高的问题，本文提出BPSK-CSK 调制方法，经过理论推导和仿真验证，证明了所提方法可有效降低传统CSK 电文解调复杂度.在信息传输速率相等的条件下，当极性比特为1 或2 时，计算复杂度降低为原来的50%或25%，此时电文解调误比特率与传统CSK 相比，其损耗可以忽略不计.当极性位数大于2 时，所提方法以解调性能为代价降低计算复杂度，但此时若结合信道编码，BPSK-CSK 仍可实现等计算复杂度下的误比特率降低，具有应用优势.