奇异元个数对线性群PSL(2，p)的刻画①

严德钰， 沈如林

湖北民族大学 数学与统计学院，湖北 恩施 445000

有限群的结构可以由群的一些特殊数量关系反映出来，例如： 同阶交换子群的个数、 与最高阶元素有关的数量条件以及特征标维数等都可以刻画群的结构[1-3]． 因此，通过群的数量特征来研究群的结构有着重要意义．

定理1设G是有限群，p是素数． 若μ(G)=μ(PSL(2，p))， 则G≅PSL(2，p)．

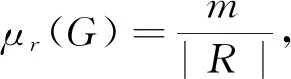
证设|G|r表示|G|的r-部分，|G|r′表示|G|的r′-部分． 由于方程x|G|r′=1的解的个数为r-正则元的个数，根据Frobenius定理[9-10]知方程解的个数是|G|r′的倍数，则G中r-正则元的个数Rr(G)为k|G|r′， 其中k为一正整数． 同样记G中r-奇异元的个数为Sr(G)， 则

下证m与r互素， 只需证r-正则元的个数与r互素． 设G的Sylowr-子群R共轭作用在G中的r-正则元Ωr上，并设轨道为O1，O2，…，Ok． 注意到Oi={xi}当且仅当CR(xi)=R， 因此G中r-正则元的个数为

其中x∈Ωr-CΩr(R)根据Schur-Zassenhaus定理知CG(R)=Z(R)×H，其中H的阶与r互素，则

CΩr(R)=Ωr∩CG(R)=H

从而Rr(G)=|H| (modr)． 故r-正则元的个数与r互素．

注1根据引理1知，若μ(G)=μ(H)， 显然有|G|=|H|．

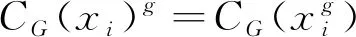
这里Rr(CG(xi))是CG(xi)中r-正则元的个数，故

引理3设p为奇素数，且r∈π(PSL(2，p))，则

以下分情况讨论μr(PSL(2，p))的值：

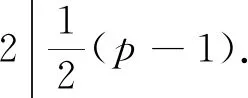
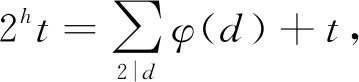
故

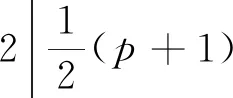
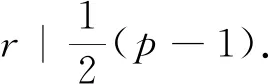
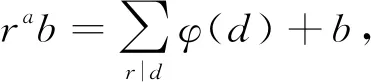
故

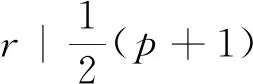
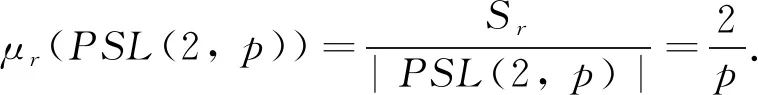
设G是有限群，定义G的素图Γ(G)：Γ(G)的顶点集为π(G)， 两个不同的顶点p，r有边相连当且仅当G中有一pr阶元，t(G)表示Γ(G)的连通分支数，πi(i=1，2，…)表示Γ(G)的连通分支所含顶点之集． 如果2||G|， 则总设2∈π1．

首先给出Frobenius群和2-Frobenius群的结构：

引理4[12](i) 设G是偶阶Frobenius群，H是Frobenius核，K是Frobenius补，则t(G)=2，Γ(G)={π(H)，π(K)}；

(ii) 2-Frobenius群可解．

以下是由Williams给出的具有非连通素图的群的结构：

引理5[13-14]设G是有限群，G的素图非连通，则G有如下3种结构：

(i) Frobenius群；

(ii) 2-Frobenius群；

(iii)G有一正规列1◁_H◁_K◁_G， 使得K/H是非交换单群，H和G/K是π1-群，H是幂零群且|G/K|||Out(K/H)|．

另外，对于非连通素图的单群的分类可参见文献[14]的表Ib-Ie，IIa-IIc、 文献[15]的表Ia，Ib，II，III以及文献[16]．

定理1的证明

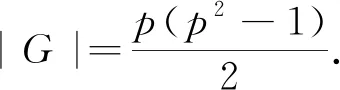
步骤1G是完全群，即G′=G．

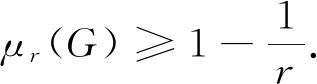
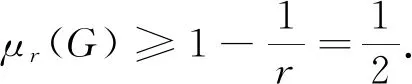
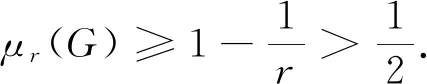
这与μr(G)=μr(PSL(2，p))矛盾．

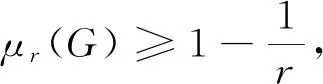
因此

即有p=r=3， 这与我们假设的p≥5矛盾．

综上所述，G/N是非交换单群，G是完全群．

步骤2顶点p是G的素图的孤立点，且G中的Sylowp-子群不正规．

证明顶点p是G的素图的孤立点等价于证明对任意素数r(≠p)，G中无pr阶元．

由于

3)基本顶组成及运动特点。由于工作面存在明显的顶板周期来压显现，因此基本顶的周期性断裂是其主要运动特征。工作面基本顶主体岩层为粗砂岩，厚度8 m，周期断裂步距约20 m。

则G的Sylowp-子群P同构于Zp． 设G的Sylowp-子群的个数为np，G中p-奇异元的个数为Sp(G)． 由Sylow定理知np≡1(modp)， 则G中p-奇异元的个数Sp(G)≥(p-1)np， 由引理3知Sp(G)=p2-1， 从而np=p+1，1．

首先假设np=p+1， 则G中的p阶元的个数为(p+1)(p-1)． 而Sp(G)=p2-1， 故G中p阶元的个数等于p-奇异元的个数，即G中无pr阶元．

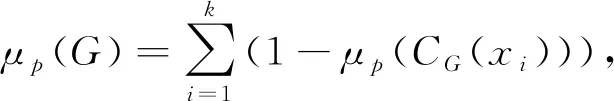
首先假设p阶元只有一个共轭类． 设x1为p阶元共轭类的代表，CG(x1)中p-奇异元的个数为Sp(CG(x1))． 由引理2和引理3知

而(p-1)|Sp(CG(x1))， 我们有(p-1)|(p-2)或(p-1)|(p+1)， 即p只能为2， 这与p≥5矛盾．

以下假设p阶元有两个共轭类． 设x2，x3为p阶元共轭类的代表． 同样由引理2和引理3知

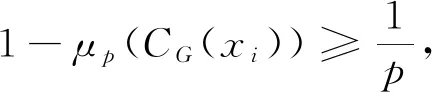
即

(1)

由于p阶元有两个共轭类，则p阶元的两个共轭类长的和为

|G∶CG(x2)|+|G∶CG(x3)|=p-1

从而

结合(1)式得

通过放缩有

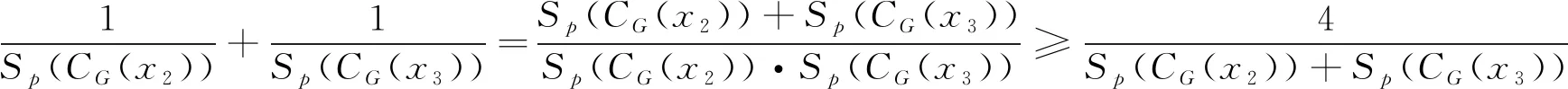
从而

即

Sp(CG(x2))+Sp(CG(x3))≥2(p+1)(p-1)

如果Sp(CG(x2))>(p+1)(p-1)或Sp(CG(x3))>(p+1)(p-1)， 则与Sp(G)=p2-1矛盾． 如果Sp(CG(x2))=Sp(CG(x3))=(p+1)(p-1)， 则由(1)式得|CG(x2)|=|CG(x3)|=p(p+1)． 由于np=1， 则P◁G． 由N/C定理知

(2)

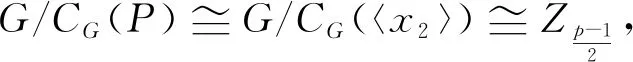
步骤3G既不是Frobenius群也不是2-Frobenius群．

首先假设G是Frobenius群且G是偶阶． 设H是Frobenius核，K是Frobenius补，由引理4知t(G)=2且Γ(G)={π(H)，π(K)}． 由步骤2知G中顶点p是孤立点，则Γ(G)={p，π(K)}或Γ(G)={p，π(H)}．

若Γ(G)={p，π(K)}， 则P是Frobenius核，从而P在G中正规， 矛盾．

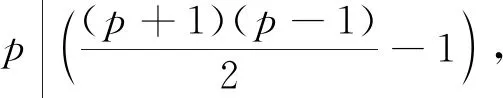
假设G是2-Frobenius群且G是偶阶． 由引理4知2-Frobenius群可解，这与G是完全群矛盾．

步骤4G≅PSL(2，p)．

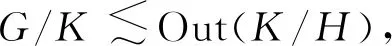
下面证明G/H≅PSL(2，p)， 显然由|G|=|PSL(2，p)|就证明了G≅PSL(2，p)． 以下s为奇素数，q为素数幂，单群的阶参见文献[17]． 我们根据素图分支的个数进行讨论．

G/H的素图为两个连通分支：

情形1G/H≅As-1(q)，其中s≥2，q为奇素数幂，或q为2的幂且(s，q)≠(3，2)，(3，4)．

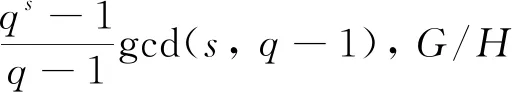
(qs-1)=p(q-1)gcd(s，q-1)

(3)

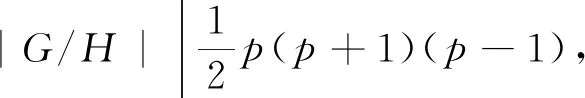
(4)

将(3)式代入(4)式，得

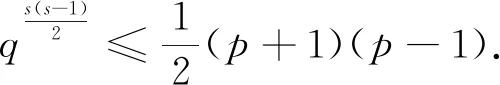
q3-1=p(q-1)gcd(3，q-1)

得

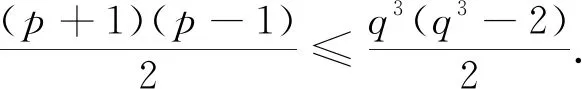
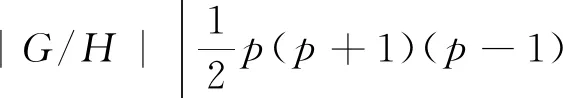
G/H≅A2(2)≅PSL(2，7)

情形2G/H≅As(q)， 其中(q-1)|(s+1)且s≥1．

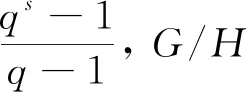
根据qs-1=p(q-1)得

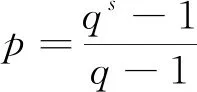
从而由整除关系易知

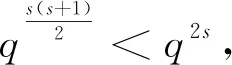
情形3G/H≅B2m(q)， 其中m≥2且q为奇素数幂．

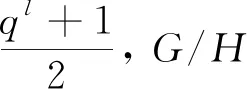
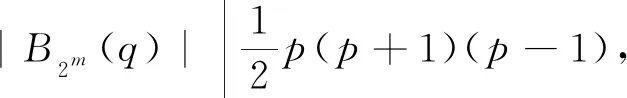
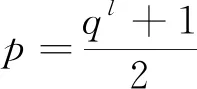
显然有(q22m，ql+1)=1， (q22m，ql-1)=1，q22m|/(ql+3)， 这与整除关系矛盾．

假设G/H≅C2m(q)， 其中m≥1，且q为奇素数幂；G/H≅C2m(q)， 其中q为2的幂． 由于|C2m(q)|=|B2m(q)|， 则证明与G/H≅B2m(q)一致．

情形4G/H≅Bs(3)， 其中s≥2．

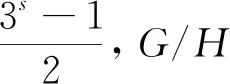
假设G/H≅Cs(3)， 其中s≥2． 由于|Bs(3)|=|Cs(3)|， 则证明与G/H≅Bs(3)一致．

情形5G/H≅2As-1(q2)， 其中s≥3．

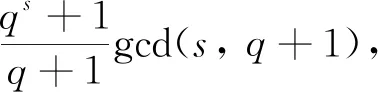
qs+1=p(q+1)·(s，q+1)

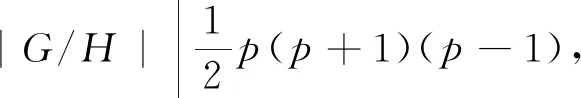
根据qs+1=p(q+1)·(s，q+1)得

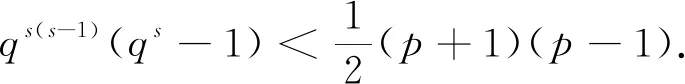
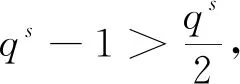
情形6G/H≅2As(q2)， 其中(q+1)|(s+1)且s≥2．

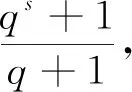
(5)

由(5)式左边得

由(5)式右边得

情形7G/H≅2D2n(q2)，其中n≥1且q为奇素数幂．

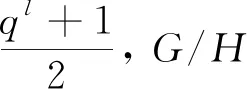
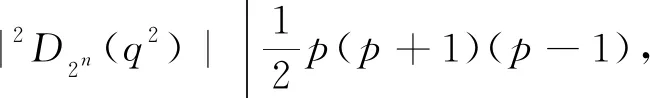
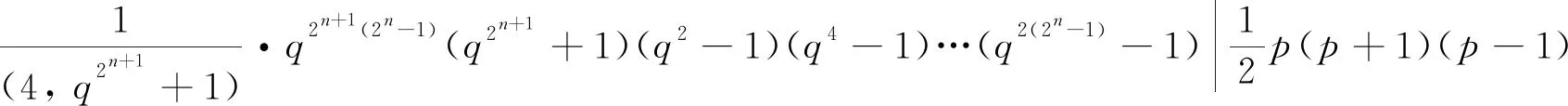
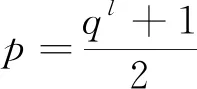
显然有q2n+1(2n-1)|/(ql-1)，q2n+1(2n-1)|/(ql+1)， 因此q2n+1(2n-1)|(ql+3)， 则q=3且2n+1(2n-1)=1． 这与2n+1(2n-1)≥4矛盾．

情形8G/H≅2Ds(32)， 其中s≥5且s≠2n+1．

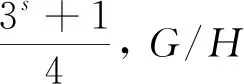
9s(s-1)(9s+1)(92-1)(94-1)…(92(s-1)-1)|p(p+1)(p-1)

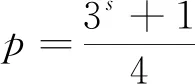
显然有9s(s+1)|/(3s+1)， 9s(s+1)|/(3s+5)． 因此9s(s+1)|(3s-3)， 即2s(s-1)只可能为1． 这与2s(s-1)≥40矛盾． 同理可证G/H≅2Dl(32)， 其中l=2n+1且l≠s．

假设G/H同构于单群S， 根据Atlas定理[17，9]知群S的阶，则S取以下群之一：

①Ds(2)， 其中s≥3， |Ds(2)|=2s(s-1)(2s-1)(22-1)(24-1)…(22(s-1)-1)；

②Ds+1(2)， 其中s≥2， |Ds+1(2)|=2s(s+1)(2s+1-1)(22-1)(24-1)…(22s-1)；

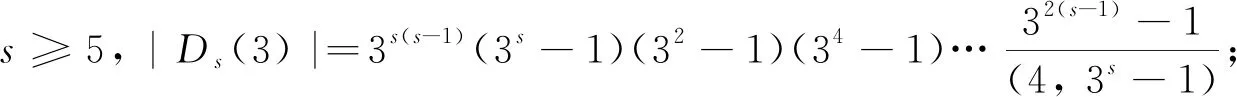
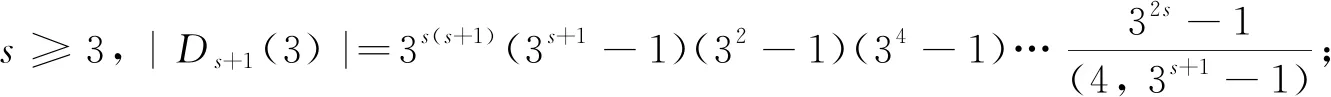
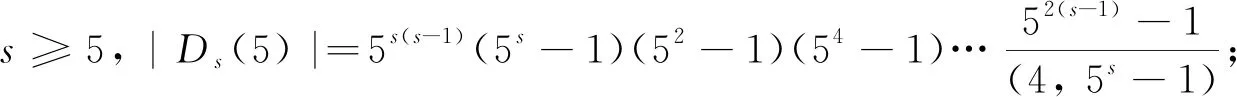
⑥3D4(q3)， 其中q为奇素数幂， |3D4(q3)|=q36(q24+q12+1)(q18-1)(q6-1)；

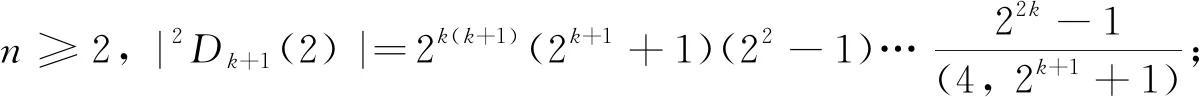
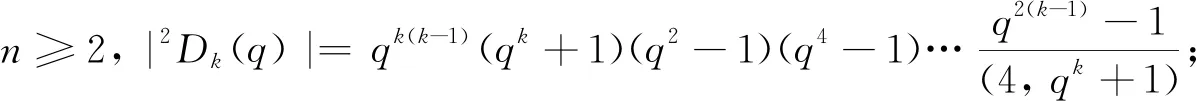
⑨G2(q)， 其中q≡±1(mod 3)且q为奇素数幂， |G2(q)|=q6(q6-1)(q2-1)；

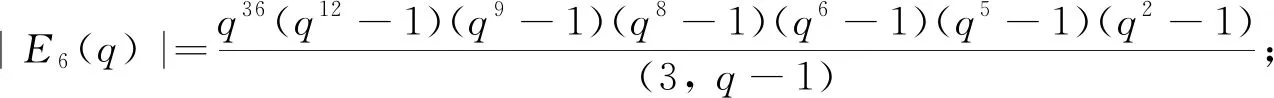
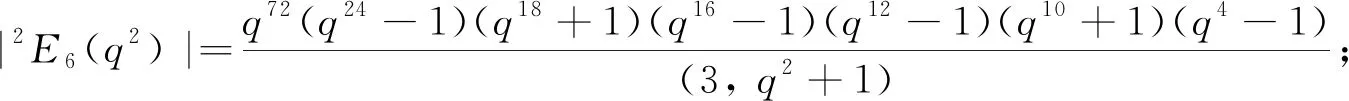
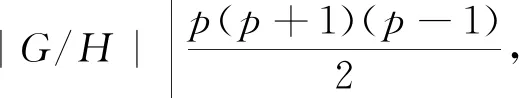
G/H的素图为3个连通分支：

情形1G/H≅Alt(n)， 其中n=5，6．

情形2G/H≅A1(q)， 其中q≡1(mod 4)且q为奇素数幂．

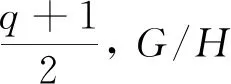
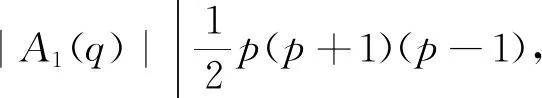
假设G/H≅A1(q)， 其中q≡-1(mod 4)且q为奇素数幂．

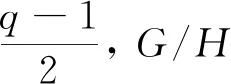
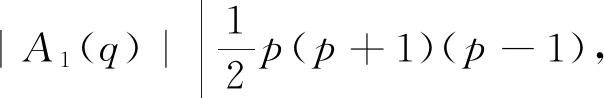
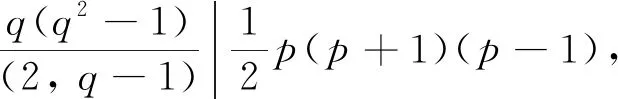
假设G/H≅A1(q)， 其中q为2的幂． 由于A1(q)的孤立点为q-1或q+1，G/H的孤立点为p， 则q-1=p或q+1=p． 又由于

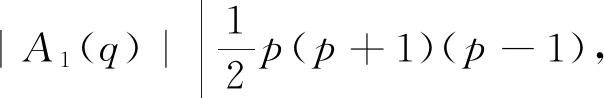
情形3G/H≅A2(2)．

由于A2(2)的孤立点为3或7，G/H的孤立点为p， 则3=p或 7=p，又由于

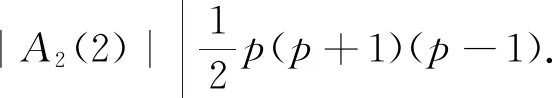
情形4G/H≅2G2(32m+1)， 其中q=32m+1且m≥1．

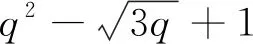
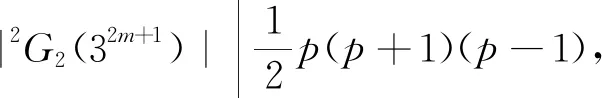
假设G/H同构于单群S， 根据Atlas定理[17，9]知群S的阶，则S取以下群之一：

②E7(2)， |E7(2)|=263×(218-1)(214-1)(212-1)(210-1)(28-1)(26-1)(22-1)；

③2F4(q)， 其中q为2的幂， |2F4(q)| =q12(q6+1)(q4-1)(q3+1)(q-1)；

④F4(q)， 其中q为2的幂， |F4(q)|=q24(q12-1)(q8-1)(q6-1)(q2-1)；

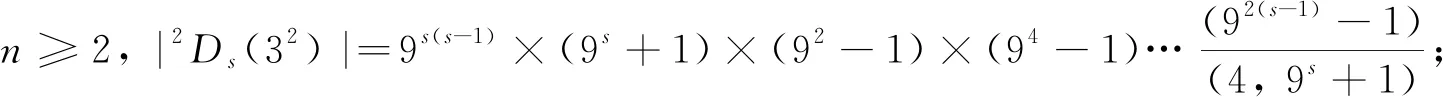
⑥G2(q)， 其中q≡0(mod 3)且q为奇素数幂， |G2(q)|=q6(q6-1)(q2-1)；

⑦2A5(22)， |2A5(22)|=415(42-1)(43+1)(44-1)(45+1)(46-1)；

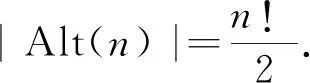
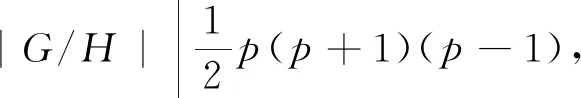
G/H的素图为4或5个连通分支：

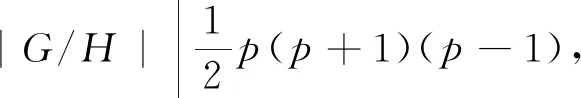
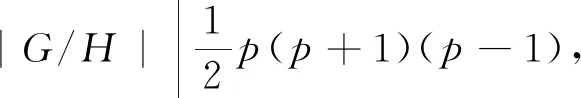
综上所述G/H≅PSL(2，p)， 从而G≅PSL(2，p)．