加权子空间的随机向量函数链接网络集成方法①

叶璇， 何玉林， 张曼静， 黄哲学

1.人工智能与数字经济广东省实验室(深圳)，广东 深圳 518107；2.深圳大学 计算机与软件学院，广东 深圳 518060

随机向量函数链接网络(random vector functional link network，RVFL)作为最早的随机权网络模型[1]于1992年在文献[2]里提出，文献[3]在此基础上进行了总结完善． 作为随机权网络代表，RVFL的输入层权重和隐含层偏置的初始值为随机生成，求解隐含层节点与输入层节点所构成的结合矩阵的伪逆并直接得到输出层权重，进而实现模型训练． 因此，RVFL具有极快的训练速度，且在文献[4]中的实验证明了其具有良好的泛化能力，能处理分类和回归任务，具有很多真实应用场景． 如何有效提升RVFL的稳定性和泛化性，具有重要研究意义．

由于RVFL的结构简单化以及模型随机化，因此当前其改进方向主要集中在改善网络结构和结合集成学习两方面：

1) 改善网络结构的代表性工作． 在网络参数选择方面，文献[5]提出了有效节点选择的RVFL改进模型，简记为I-OI-RVFLNs． 该模型首先引入正交化方法对隐含层输出矩阵进行正交化，显著提升模型的收敛速度；其次预先设置隐含层节点个数并迭代更新输出层权重，裁剪冗余节点以实现网络精简化，提升模型的计算效率． 文献[6]于2017年提出了一种基于贝叶斯法则的RVFL改进模型，其在训练阶段获取额外先验知识得到最优权重的概率分布，并在测试阶段线性搜索出合适的正则化因子，进而构造网络模型并使其获得更好的预测性能． 在网络层数方面，文献[7]基于RVFL网络框架以及自编码器概念，首次提出了深度RVFL网络，简记为sdRVFL． sdRVFL引入了去噪准则，即不同的正则化法则，先对数据特征进行深层次的提取，然后将该部分特征输入到原始的RVFL进行预测，从而实现网络结构的深度化． 在sdRVFL的基础上，文献[8]于2021年提出了另一种深度RVFL网络，简记为dRVFL． dRVFL将网络中每一层所提取到的数据特征，进行横向拼接构成拼接矩阵，并利用最小二乘直接计算输出层权重，从而完成dRVFL的训练． dRVFL充分利用每层网络所提取的信息，有效提升了RVFL的泛化能力． 此外，文献[9]提出了另一种新型的深度RVFL网络，简记为FAF-DRVFL． FAF-DRVFL结合迁移学习来进行数据预处理工作，并使用模糊激活函数代替常用的Sigmoid激活函数来计算隐含层输出，有效提高了模型的稳定性以及计算效率．

2) 结合集成学习的代表性工作． 文献[10]于2020年提出了一种基于自适应机制的集成RVFL模型． 该模型根据RVFL的预测准确率来分配不同权重，若样本被错误分类则在下一次训练中给予更大的权重，以此完成模型的集成优化． 文献[11]基于残差网络机制，对数据特征进行有效提取，同时在每个基模型dRVFL的输出层参数中添加噪声扰动，增加集成多样性，从而实现对集成dRVFL(edRVFL)网络模型泛化能力的改进．

若在RVFL网络结构上进行改进，会改变其简单的模型结构，增加过拟合的风险；若结合集成方法对RVFL进行改进，又因无法增大基学习器差异性导致无法提升模型的稳定性和泛化性． 为了在不改变RVFL简单结构的条件下有效提升RVFL的稳定性和泛化性，本文提出了一种加权子空间的随机向量函数链接网络集成方法(weighted attribute bagging-based random vector functional link network，WAB-RVFL)，为优化所选属性子空间使其更适应于RVFL的网络结构，提出属性优化的思想，引入属性加权矩阵概念，提出加权子空间选择策略，搜索得到更优的加权子空间，使其能在RVFL的线性映射与非线性映射之间找到平衡点． 为寻找最优的属性加权矩阵，本文利用训练集和验证集信息构建目标函数，并采取粒子群优化算法迭代及最小化目标函数，从而搜索得到最优属性加权矩阵． 本文在8个分类数据集上展开有说服力的实验，分别验证WAB-RVFL的可行性、 合理性和有效性． 实验结果表明，WAB-RVFL具有更优的泛化能力．

本文的组织结构如下： 第1节对RVFL和贝叶斯子空间选择策略的原理进行介绍和分析；第2节对本文提出的WAB-RVFL进行详细介绍；第3节对WAB-RVFL的性能进行实验验证；第4节进行总结并给出未来研究工作．

1 相关理论知识

1.1 随机向量函数链接网络

传统神经网络基于误差反向传播算法进行权重的迭代更新，虽然能够较好地实现复杂的非线性映射关系并完成表征学习任务，但却具有训练时间长、 易陷入局部极小值等缺点． RVFL是一种特殊的单隐含层前馈神经网络，其结构特点是输入层同时与隐含层、 输出层进行直接连接，具体如图1所示． 由于避免了权重的迭代更新，因此RVFL具有极快的训练速度、 良好的函数拟合能力．

图1 RVFL的网络结构

RVFL的训练步骤主要分为3个阶段： 随机初始化阶段、 隐含层和输入层结合矩阵计算阶段、 目标输出层权重计算阶段． 首先是随机初始化生成并固定输入层权重和隐含层偏置，然后通过将数据样本进行非线性映射得到隐含层输出矩阵，最后通过最小二乘法直接解析求得目标输出层权重．

假设有一个分类数据集容量大小为N，其具有D维属性以及M个类标：

S={(xn，tn)|xn=(xn1，xn2，…，xnD)，tn=(tn1，tn2，…，tnM)}

(1)

1) 随机初始化阶段． 首先按照一定分布随机初始化RVFL的输入层权重和隐含层偏置，分别表示为

(2)

和

(3)

2) 隐含层和输入层结合矩阵计算阶段． 数据样本经过输入层权重和隐含层偏置转换后，进行非线性映射得到隐含层输出矩阵：

(4)

其中

(5)

g(·)表示激活函数，通常使用Sigmoid函数：

(6)

因此，隐含层和输入层结合矩阵表示为

GN×(L+D)=[HN×L，XN×D]N×(L+D)

(7)

其中X=(xnd)N×D是样本输入值． RVFL的整个计算过程可以表示为

GN×(L+D)β(L+D)×M=YN×M

(8)

其中：β(L+D)×M是目标输出层权重，YN×M是样本预测值．

3) 目标输出层权重计算阶段． 输出层权重是整个RVFL训练求解的核心部分．T是样本真实值，为使样本预测值和样本真实值尽可能接近，需最小化以下目标函数：

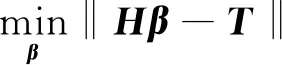
(9)

通过最小二乘法解析求解，得到输出层权重为

(10)

为了更好平衡经验风险和结构风险，往往在求解过程中加入正则化因子进行计算，此时输出层权重计算表示为

(11)

由RVFL训练过程可知，RVFL不进行权重迭代调整，从而获得了极快的训练速度． 已有实验结果表明，RVFL具有良好的泛化性能[4]，万能逼近能力理论也证明了RVFL的收敛性[12]．

1.2 贝叶斯子空间选择策略

随机子空间方法是一种常用的有效降低数据集维度的策略，能够减小数据训练复杂度，提升模型测试精度． 随机子空间方法基于集成学习策略实现，通过获取多个随机属性子空间，用于多个基学习器训练并对预测进行融合，从而得到更稳定、 更精确的最终模型．

贝叶斯子空间选择(bayesian attribute bagging，BAB)策略，是文献[13]在贝叶斯法则的基础上所提出的一种有效的子空间选择策略． 基于贝叶斯法则计算条件属性与决策属性之间的属性决策度(decision-making degree，DMD)；根据最大DMD来生成最优的条件属性组(condition attribute group，CAG)；对得到的CAG按一定比例进行抽样，生成多个Bagging属性组(bagging attribute group，BAG)，此时BAG即为得到的目标属性子空间．

不同于传统的属性Bagging策略对条件属性进行随机抽样，BAB充分考虑条件属性与决策属性之间的影响程度，得到的属性子空间更均衡、 更稳定，在后续的基学习器训练中会取得更佳的性能．

2 加权子空间的随机向量函数链接网络集成方法

BAB策略能够有效获得更均衡、 更稳定的属性子空间，但由于RVFL网络结构具有输入层和输出层直连的特点，因此在训练过程中，输入属性具有线性映射和非线性映射两部分性质． 若简单将BAB和RVFL进行结合，则会忽略掉该线性映射部分的特性． 为了更好结合BAB策略与RVFL的网络结构特点，本文在BAB的基础上提出了加权子空间选择(weighted attribute bagging，WAB)策略，用以构造加权子空间的随机向量函数链接网络集成模型(weighted attribute bagging-based RVFL，WAB-RVFL)．

2.1 加权子空间选择策略

2.1.1 属性加权矩阵

RVFL的网络结构具有输入层到输出层、 隐含层到输出层两部分目标输出权重，因此其同时具有线性映射和非线性映射的特性． 对于BAB所得到的属性子空间，并不完全适合RVFL模型训练，为更贴合这两部分特性，应该采取有效的策略进行属性子空间的优化转换． 对适合线性映射部分的属性进行加权放大增强，对不适合线性映射部分的属性进行加权减小抑制，从而实现更优模型的训练．

为了得到用于集成模型训练的更有效的属性子空间，本文引入属性优化思想，提出属性加权矩阵的概念，用于属性子空间的加权转化，其形式为

(12)

其中D为子空间属性个数． 对于子空间输入样本X，利用属性加权矩阵对其进行属性加权，转化后的加权子空间可以表示为：

(13)

属性加权矩阵是一个对角阵，其对角线上的元素为子空间输入样本各个属性的加权． 在属性加权矩阵的作用下，针对于RVFL特有的两部分结构，若某些属性适合线性映射，则其属性加权应该增大；若某些属性适合非线性映射，则其属性加权应该减小． 如何找到合适的属性加权矩阵是加权子空间选择策略的核心．

2.1.2 目标函数设计

在机器学习任务中，目标函数是一个用来衡量模型拟合程度的函数，通常如果函数值越小则表示模型的拟合效果越好． 如何有效最小化目标函数非常关键．

在属性加权矩阵的搜索过程中，本文利用训练集和验证集信息来构建目标函数，具体形式为：

(14)

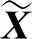
为搜索最优的属性加权矩阵，本文选取粒子群优化(particle swarm optimization，PSO)算法[14]进行迭代优化，利用搜索得到属性加权矩阵Q，使其对子空间的属性进行加权转化，起到增强或抑制的作用，从而获得加权后更优质、 更适合RVFL网络结构的属性子空间．

2.2 WAB-RVFL算法流程

WAB-RVFL算法的核心是利用PSO迭代优化搜索得到最优的属性加权矩阵，为更好地展示WAB-RVFL算法，具体的流程如算法1所示．

算法1: WAB-RVFL算法1 基于贝叶斯子空间选择(BAB)策略, 得到K个属性子空间BAGs; 2 基于加权子空间选择(WAB)策略, 对K个BAGs进行加权优化: 3 fork=1 to Kdo4 基于属性子空间BAGk, 进行PSO迭代更新搜索得到属性加权矩阵Qk; 5 利用属性加权矩阵Qk, 对BAGk进行加权得到优化后的BAG k. 6 end for7 基于优化后的加权子空间, 进行RVFL集成训练和预测: 8 基于K个BAG k, 构建K个RVFL模型; 9 fork=1 to Kdo10 利用训练好的RVFLk, 对新样本进行预测得到y(k). 11 end for12 对于K个RVFL的预测y(1),y(2),…,y(K), 计算信息量权重v1,v2,…,vK并进行加权融合输出[13]: y=∑Kk=1vky(k)

3 实验验证与分析

本次实验在8个高维分类数据集中开展，数据集信息如表1所示[15]． 本文对数据集进行清洗，并为减少训练时间采取随机抽样方式得到小规模数据集，用于模型的训练和测试． 数据被划分成了80%训练集和20%测试集，并采用最大最小归一化方法，将属性区间缩放到[0， 1]． 本实验采取准确率(Accuracy)作为模型的衡量标准，且所有实验均是重复5次试验的平均结果．

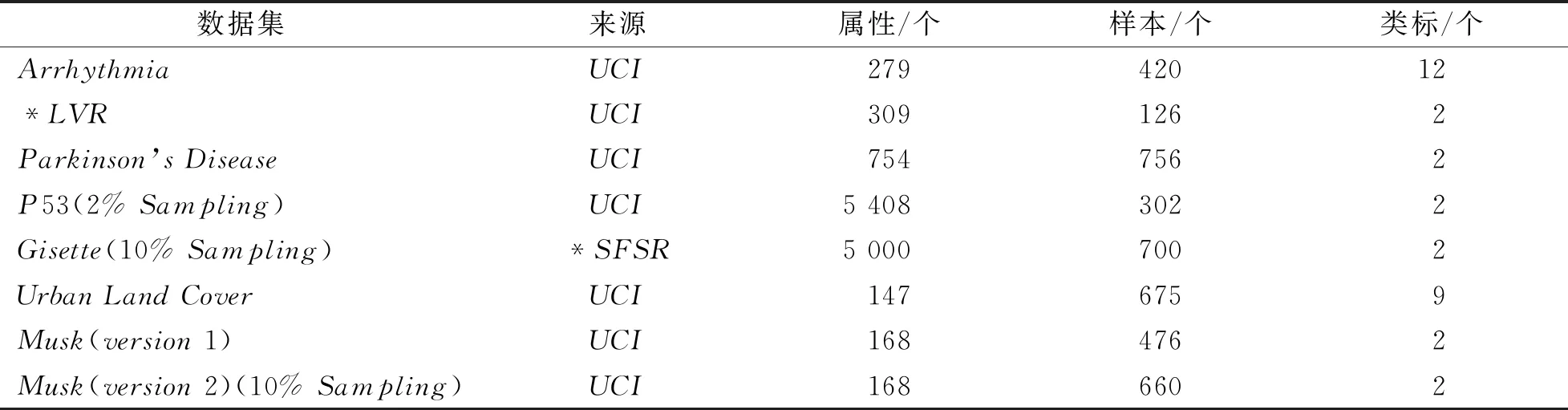
表1 数据集信息

PSO算法的实验参数设置如下： 种群迭代次数为200，种群大小为50，个体值区间为[0， 2]，速度值区间为[-0.2， 0.2]，惯性因子为0.729 8，学习因子均为1.494 45． 将训练集以0.5的比例划分得到验证集用于目标函数的迭代优化． 通过10次重复试验遍历RVFL得到最优精度对应的节点个数． 在WAB-RVFL实验中将BAB策略的特征抽样比例参数设置为0.8．

3.1 WAB-RVFL可行性验证

在WAB-RVFL中，如何有效最小化该目标函数非常关键． 本文采取PSO优化算法对目标函数进行迭代最小化，从而实现最优属性加权矩阵的搜索，优化属性子空间而进一步提升模型性能． 本文选取了4个数据集进行迭代优化展示，具体如图2所示．

从图2可以看出，随着迭代次数的增加，目标函数值逐渐优化减小；在迭代次数为150之后，图像基本上趋于收敛状态． 这表明WAB-RVFL所构造的目标函数是有效的，其随着PSO的优化迭代而不断减小，验证了WAB-RVFL算法的可行性．

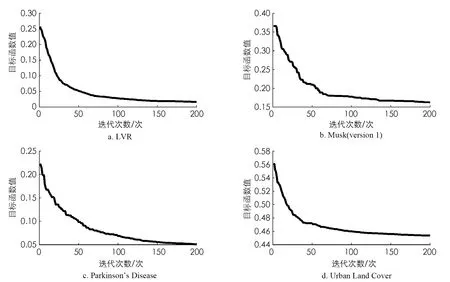
图2 在PSO优化下目标函数值的迭代展示

3.2 WAB-RVFL合理性验证

为了验证WAB-RVFL的合理性，本节对3种基模型进行了比较，即Single RVFL模型、 Single BAB-RVFL模型和Single WAB-RVFL模型，其分别是基于投票策略的RVFL(Voting-RVFL)、 基于贝叶斯子空间的RVFL(BAB-RVFL)和基于加权子空间的RVFL(WAB-RVFL)3种集成模型的基学习器． 具体的实验结果如图3所示．

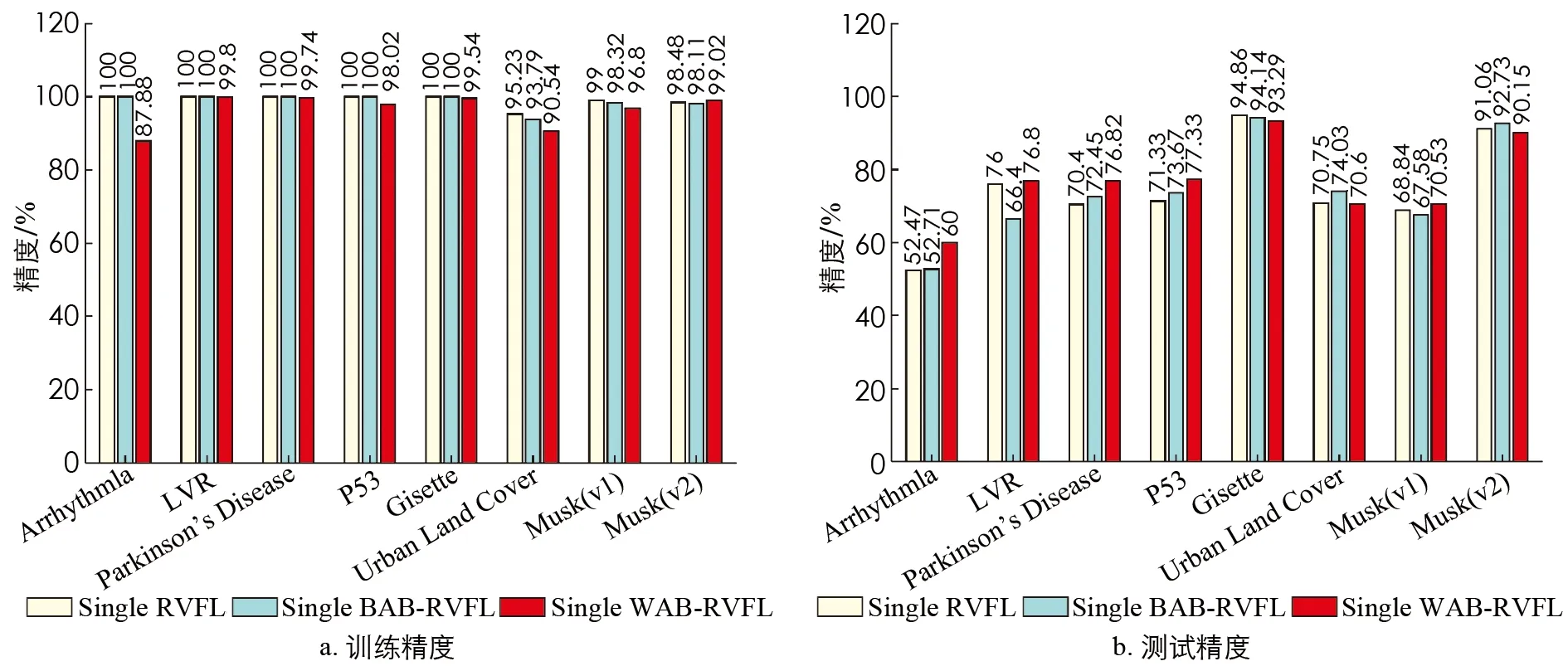
图3 3种基模型在8个分类数据集下的比较

由图3可知，在训练部分，Single RVFL和Single BAB-RVFL在5个数据集上的精度达到100%，Single WAB-RVFL的训练精度普遍较低，只有在Musk(version 2)数据集中表现比其他两个模型高；在测试部分，Single WAB-RVFL则在多个数据集下普遍表现比其他两个基模型的要好，即精度更高． 在Musk(version 2)，Urban Land Cover和Gisette 3个数据集中，虽然Single WAB-RVFL测试精度不是最高，但与Single RVFL相比较为相近．

总结分析得，WAB-RVFL的基模型Single WAB-RVFL经过属性加权矩阵的优化之后，在8个数据集的测试集上有5个表现要比Single RVFL和Single BAB-RVFL好，其中3个数据集上表现均与Single RVFL相差不大． 这说明本文提出的属性加权矩阵和WAB-RVFL模型具有合理性，属性加权矩阵能够较好地对子空间进行加权优化，从而提升模型的测试精度． 这为下一小节中验证最终集成模型的性能提供了合理性依据．

3.3 WAB-RVFL有效性验证

在上一小节中的WAB-RVFL合理性实验，分析得到Single WAB-RVFL在大多数数据集上比Single RVFL和Single BAB-RVFL性能更佳． 本小节将通过丰富的模型对比实验，验证WAB-RVFL的有效性．

本文搭建实验平台，将WAB-RVFL与以下6个模型： RVFL，Voting-RVFL，Bagging-RVFL，dRVFL，edRVFL以及BAB-RVFL进行比较，其中dRVFL和edRVFL的隐含层层数设置为10，具体的实验结果如图4所示．

图4 在分类任务中WAB-RVFL与其他RVFL模型的比较

由图4可知，随着基学习器的增加，所有RVFL集成算法均趋于收敛，表明RVFL结合集成方法的应用是可行的，模型精度能够不断提升并趋于稳定状态． 本文提出的WAB-RVFL在8个高维分类数据集下，与其他RVFL模型相比，均能取得更高的预测精度． 实验结果表明，加权子空间选择策略能有效缓解模型过拟合现象，WAB-RVFL具有更佳的泛化性能，验证了WAB-RVFL的有效性．

本文还使用Nemenyi检验方法[16]来进行多个模型之间的统计检验分析，显著性水平设置为0.1，CD值表示为临界差值区间，固定基学习器为50，取测试集精度进行模型比较． 由图5可知，在测试过程中，WAB-RVFL和BAB-RVFL共处同一临界差值区间，且WAB-RVFL的平均秩值更小，其他模型则分别与WAB-RVFL处于不同的临界差值区间，这表明WAB-RVFL的预测性能优于BAB-RVFL；与其他5种模型的差异较大，且均优于这5种模型． 因此，本文提出的WAB-RVFL具有更稳定且更优的预测性能．

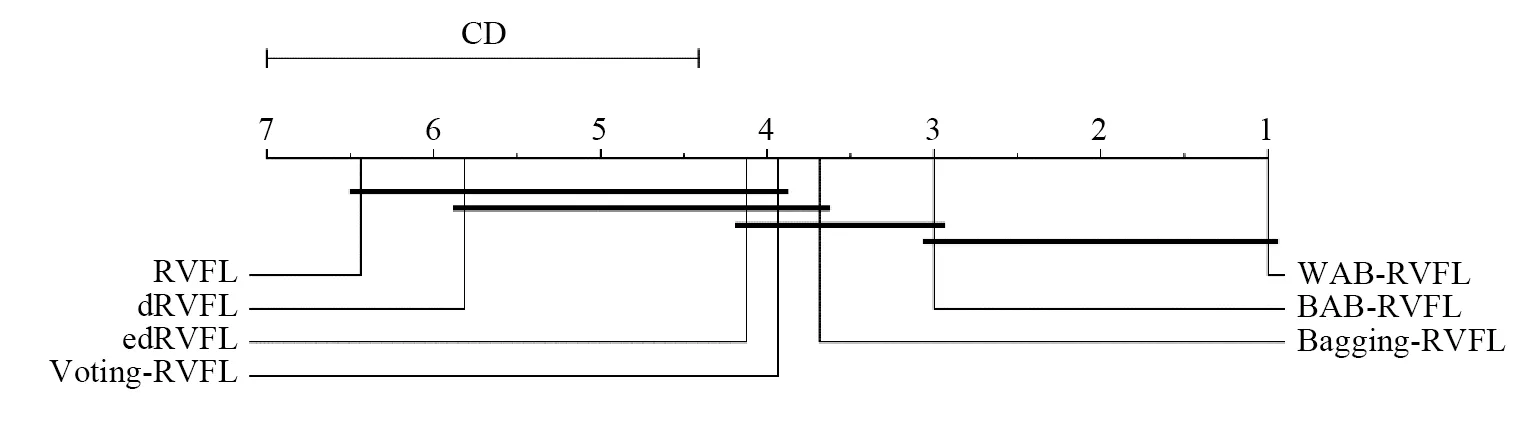
图5 模型测试精度的统计检验结果

4 结论与未来工作

本文基于RVFL输入层和输出层直连的结构特点，提出了一种有效的、 鲁棒性更强的加权子空间的随机向量函数链接网络集成方法(weighted attribute bagging-based random vector functional link network，WAB-RVFL)． 首先，基于贝叶斯子空间选择策略，对RVFL结构进行分析并提出合适的加权子空间选择策略，引入属性加权矩阵概念，构造有效的目标函数并利用PSO算法迭代优化；其次，设置3个实验验证了WAB-RVFL的可行性、 合理性和有效性． 实验结果表明，PSO对目标函数迭代优化收敛证明了WAB-RVFL的可行性；在多个数据集下，3种基学习器的对比实验中Single WAB-RVFL预测性能更好，体现了WAB-RVFL的合理性；在7种RVFL模型的对比实验中，WAB-RVFL具有更高测试精度，验证了WAB-RVFL的有效性．

在本文中仍有部分内容值得进一步地探究，未来的工作展望主要有以下两点：

1) 其他智能算法的使用． 针对WAB-RVFL模型中使用到的经典PSO优化算法，探究是否能使用其他更优的智能算法进行模型的迭代优化，减少实验的开销，提升模型的性能；

2) 大规模数据的处理． WAB-RVFL模型具有并行运算的潜力，而目前在大数据时代下对模型精度以及运算效率要求都特别高，因此接下来将考虑是否能将本文提出的两种模型，在大数据框架下进行分布式计算，处理真实的大数据问题．