串联新旧知识，激发复习课的生长点

梁 希

江苏省如皋经济技术开发区实验初中 226500

复习课是教学中的重要环节，对于学生巩固复习旧知，构建知识体系，深化对知识的认识起着关键性的作用.然而复习课却常常陷入“炒冷饭”的误区，课堂沉闷枯燥.教师将学生已学知识进行简单的罗列，或者将复习课变成习题讲解课，影响了复习课的效率，达不到真正的复习效果，反而浪费了课堂的教学时间.笔者在教学中进行了一些尝试，通过教学设计的试讲、修改，不断提升复习课的效果，落实培养学生核心素养的目标，现将修改教学设计的过程进行呈现，与各位同行进行交流探讨.

教学设计初稿

（一）试题练习复习一元二次方程根与系数的关系；

（二）求解对称式与非对称式的值，体会数学化归思想；

（三）判别含参数的一元二次方程的实数根；

（四）求解一元二次方程整数根的问题；

（五）课堂小结提升.

设计意图以习题的方式进行一元二次方程知识点的复习，通过不同板块的设计，以问题引导学生进行探究，培养学生自主学习的能力，渗透数学思想和数学方法，提升学生运用知识的技能，为二次函数的学习打下良好的基础.

试讲之后的改进方案

（一）计算题化繁为简

选取典型试题引导学生进行讨论：

案例1已知方程x2+3x-99=0有两个实数根α和β，并且α＜β，请计算下列各式的值：（1）α+β；（2）（4）α2+2α-β.

师：同学们还记得学习一元二次方程时计算过方程的根，如果已知方程x2+3x-1=0的两个实数根是α和β，那么α与β的和是多少？说一说理由.

师：那么α与β的积呢？

师：很好，这个是对称式，可以先进行通分，再利用根与系数的关系进行计算.因此我们可以进行公式的提炼，若一元二次方程ax2+bx+c=0（a≠0）的两实数根是α与β，可以得到，那么同学们知道的值是多少吗？

生3：因为（α-β）2=（α+β）2-4αβ=13，所以的值为

师：你是怎么想到要这样计算的呢？

生3：因为我们知道了α与β的和与α与β的积，我就想到了学过的两个数的差的平方与两个数的和的平方之间的关系.

师：学会了联想，非常好！虽然α-β也是一个对称式，但是无法直接求解，需要对它进行变形，变成α与β的差的平方，因此我们可以继续推广到一般的情形：若一元二次方程ax2+bx+c=0（a≠0）的两实数根是α与β，那么的值等于

那么我们还有其他方法求α-β 的值吗？

师：非常精彩！这个结论我们在今后的学习中将会经常用到，请同学们要加深印象.

下面我们再来想一个问题，刚才我们解决的都是对称式的结构，那么如果是非对称式α2+2α－β的值是多少呢？

生5：因为α是方程的实数根，所以α2+3α－1=0，经过求解可以得到α2+2α=1－α，代入原式可以得到1－α－β=1－（α+β）=1-（－3）=4.

生6：利用根的定义可知，因为α是方程的实数根，所以α2+3α－1=0，化简可以得到α2=1－3α，代入原式可以得到结果为4.

师：两位同学的解答都非常精彩，在解题的过程中体现了等量转换和化归的思想.

改进后的教学设计，通过“问题串”的设计，引导学生一步步深入探究一元二次方程的解答过程，让学生在解题的过程中逐渐理解了问题的本质.同时，通过解题引导学生进行观察和总结，让学生理解结论的由来，减少了热身的题目数量，真正体现了减负增效，并且渗透了数学思想和数学方法的学习.

（二）前后联系，引导深入探究

复习课不是新课的重新讲授，也不能变成简单的习题课，复习课是引导学生进行深入探究，去发现和解决问题，提升对问题的认识.

师：好的，那么接下来应该怎样继续计算才能求出最值呢？

生9：可以进行配方求解.原式=2（m2+4m）=2（m2+4m+4－4）=2（m+2）2－8，因为（m+2）2≥0，所以当m=－2时，2（m+2）2－8的最小值是－8.

师：同学们觉得这个答案有问题吗？

生11：这个答案有问题，这个一元二次方程有实数根的前提是Δ≥0，但是刚才的答案没有考虑Δ.

师：观察得很仔细，在Δ≥0的前提下，这个方程才有实数根，所以上面的结论还正确吗？

（学生纷纷陷入思考，觉得很有难度）

师：那我们一起来看一下函数y=2（m+2）2－8，说一说它的性质是什么？

生12：它的图像是一条开口向上的抛物线，它的对称轴是直线x=－2，顶点坐标是（－2，－8）.在对称轴的左侧和右侧，y分别随x的增大而减小和随x的增大而增大.因此当x=－2时，y的最小值是－8（如图1）.

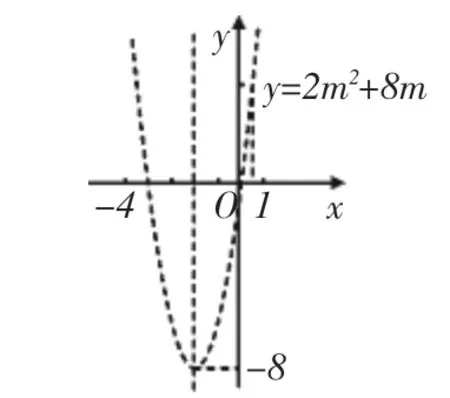
图1

生13：在这段曲线的右侧，y随x的增大而增大，所以在这条曲线上我们可以发现最低点，因此当m=的最小值是

经过改进后的教学设计使学生在教师的引导下开展探究活动，问题更具开放性，学生的主体地位得到尊重，自主学习能力得到提升，从一元二次方程的学习过渡到二次函数的学习，新旧知识产生联系，衔接自然，加深了学生对知识的理解，将方程和函数知识进行了串联，构建起新的知识体系.

教学反思

教师在课堂中的主导地位主要体现在能够给学生创设一个主动探究、理解数学的环境，充分调动学生的学习积极性，在复习课中发现新的学习增长点.

复习课不是简单的知识重复，最忌讳无意义的重复，消耗学生的学习热情，那么如何才能让复习课上出新意，让复习课触发学生新的增长点呢？笔者认为：

首先，教师要钻研教材，明确教学目标.部分教师常常忽略教学目标的确定，使得很多复习课非常随意，以至于浪费时间.有的教师把复习的知识挨个重复，有的教师准备了一系列习题，学生做到哪里算哪里，这都偏离了复习课的目的.教师在准备复习课时，同样要准备好复习课的教学目标，从哪些知识点展开，通过哪些活动培养学生的学习能力，知识之间进行怎样的联系等，只有精心准备才能提高学生的复习效率.

其次，数学复习课需要教师设计教学活动，教学活动是达成教学目标的重要抓手和载体.在数学活动中激发学生的学习兴趣，这是复习课是否达到效果的关键之一.教师可以巧妙地设计问题，通过问题引领将新旧知识进行串联，将复习课进行拓展和延伸，触发学生新的增长点，发挥复习课最大的效果.复习课上也可以通过创设情境，从学生熟悉的知识进行导入，让学生能够快速地进入复习的状态，并自觉进行新旧知识的串联.此外还可以设计探究活动，让学生在探究中体会数学思想和数学方法.总之，丰富多样的活动可以有效提高课堂效率.

最后，数学复习课需要进行典型题的训练和评析，试题练习是复习课中不可回避的重要环节，但是在试题选择上，要注重典型性和引导性，从典型试题中复习知识，发现学生知识的漏洞，培养学生应用知识的能力.试题的训练并不是最终的目的，教师让学生在习题练习中学会自主分析和解决问题，提高解题能力才是复习的目标.因此在习题练习之后教师的评析就显得尤为重要，根据学生的困惑和错误，教师要进行有重点的分析和总结，从试题中引导学生进行归纳，总结数学的解题思路，发现数学的规律，真正理解数学的本质.

综上所述，数学复习课是提升学生对知识的认知能力，巩固内化所学，感悟数学思想的关键环节.在教学中教师要钻研教学目标，了解学情，在学生已有知识的基础上弥补缺漏，并引导学生进行总结和探究，建构起知识体系和数学模型，不断增强学生对数学的兴趣，提升综合素养.