延崇高速公路金家庄特长螺旋隧道温度场分布规律及保温层研究

马印怀，林 铭，姜逸帆，张国祥，国 莉，王志杰, *，雷飞亚，周 平

(1.河北省高速公路延崇筹建处，河北 张家口 075400；2.西南交通大学 交通隧道工程教育部重点实验室, 四川 成都 610031)

0 引言

寒区隧道频发的冻害现象严重影响了隧道运营的安全性及后期维护的经济性。而温度要素是寒区隧道冻害现象发生的根本原因，因此研究寒区隧道温度场分布规律十分必要。基于此，学者们对隧道的温度场进行了不同方向的研究。

其中，现场测试是温度场规律探究最重要的方法。丁浩等[1]采用现场测试的方法，揭示了隧道内温度扩散规律。宋鹤等[2]通过温度监测，在对隧道纵向、径向温度分布规律进行研究的同时，讨论了保温层的效果。Zhao等[3]在兴安岭隧道进行了温度场测量，揭示了温度场的时空特征，并建立了基于斯蒂芬法的冻结深度计算公式。马志富等[4]通过对高纬度寒区隧道监测数据分析提出隧道洞口的相对高差引起的自然气压差是影响隧道洞内纵向温度场分布的主导因素。

理论推导能够在揭示温度传递机理的同时，方便进行温度场预测。张国柱等[5]通过合理假设建立传热模型，推导围岩径向温度的理论公式并予以验证。于丽等[6]结合流体传热原理，根据能量守恒原理，推导寒区隧道风流温度场的传热模型。Zhou等[7]通过建立非稳态有限差分模型，探究了机械通风及列车诱导风对温度场的影响。韩跃杰等[8]根据热传导理论，建立隧道径向传热模型，利用温度场叠加和拉普拉斯变换相结合的方法，提出隧道径向温度场理论解。

此外，模型试验也是隧道工程研究的重要手段，但在寒区隧道的研究中运用不多。高焱等[9]设计了适用于寒区铁路隧道的模型试验，实现了对多因素影响下的温度场分析。Zeng等[10]借助相似模型试验，分析了不同进风口条件下的温度场。郭瑞等[11]通过研制模拟室内模型试验装置，分析了隧道长度、洞口气温和风速对寒区隧道纵向温度场分布的影响及其规律。

也有不少学者通过数值模拟对寒区隧道温度场的影响要素进行分析。孙克国等[12-13]深入研究围岩特性、支护结构导热系数对温度场分布的影响。李思等[14]进一步地采用数值仿真方法对围岩热学参数的影响敏感度进行了系统研究。张晨曦等[15]通过对西成铁路沿线20座隧道温度场进行了计算分析，探究了热位差对寒区隧道温度场分布的影响。

现阶段对于寒区隧道的温度场研究多针对于直线隧道且相对成熟，但对于曲线隧道温度场分布规律的研究较为少见。而且，由于曲线隧道内空气流动规律与直线隧道大不相同[16]，必然会对隧道温度场的分布造成一定程度的影响。因此，本文依托金家庄特长螺旋隧道，采用现场监测方法，结合数值模拟手段建立三维流固耦合瞬态传热模型，探究曲线隧道的温度场分布规律，并基于冻结长度拟合保温层长度计算公式，以期为类似特殊几何尺寸寒区隧道工程的抗防冻设计提供解决方向。

1 工程概况

金家庄特长螺旋隧道位于延崇高速公路河北段西北方向，为分离式特长隧道。隧道左幅ZK80+398～ZK84+626，长4 228 m，左线进出口设计高程分别为1 403.919、1 481.714 m；隧道右幅K80+386～K84+490，长4 104 m，进出口设计高程分别为1 403.808、1 482.194 m。隧道最大埋深为314.5 m，为克服高差，采用螺旋式结构。其分布走向如图1所示。隧址区总体起伏较大，围岩整体性较差。其中，Ⅳ级围岩占72%，Ⅴ级围岩占12%，Ⅲ级围岩占16%。隧址年最高气温与年最低气温分别可达39.4 ℃和-28.2 ℃，年平均气温为5.5 ℃。其最大积雪与冻土深度分别为9、162 cm。

2 温度场监测方案

2.1 洞口气象监测

结合隧道现场实际状况，采用PC-4型便携气象站监测。根据金家庄特长螺旋隧道实际情况，在距离隧道进口及出口50 m处各安装1台气象站，如图2所示。现场使用时，该装置能够快速拼装、拆卸。此外，该设备还具有网络数据传输等一系列特点，能够采集隧址的风速、风向、温度等重要数据。

2.2 衬砌表面空气温度测试

采用RC-5温度记录仪测试隧道衬砌壁面空气温度(见图3)，记录仪安装于固定在隧道衬砌表面的铁皮箱中。温度场监测断面设置在隧道左线，其贯通时间为2019年6月18日。设定每2次监测间隔为1 h。衬砌表面空气温度监测断面设置里程见表1。

(a)RC-5温度记录仪 (b)温度现场采集

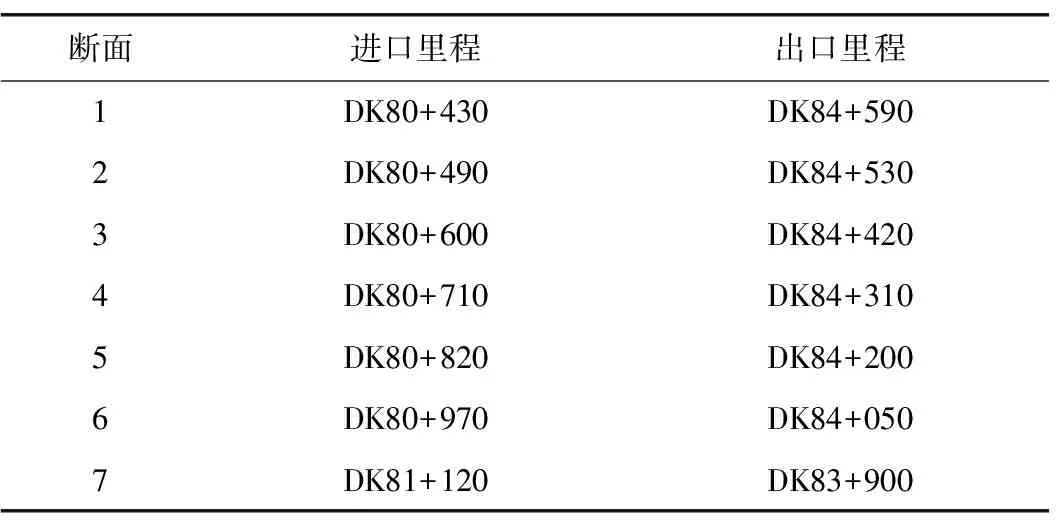
表1 衬砌表面空气温度监测断面设置里程

3 温度场监测结果分析

3.1 隧道洞口气象

汇总气象站监测1年的隧道进出口现场数据，绘制成隧道洞口气象温度采集图,如图4所示。由图可知，在12月及1月主要为西北风，此时进出口均为背风面，风速多为1—2级。此外隧道进出口温度时程变化曲线大体上符合正弦函数变化规律。该隧道进口最冷月的日平均温度为-16～-14 ℃，而出口为-13～-11 ℃；另一方面，隧道进口夏季日平均温度为16～18 ℃，出口为19～21 ℃。

(a)隧道进口风速

3.2 衬砌表面空气温度

根据现场测试数据，寒区隧道衬砌壁面空气的温度时程变化曲线基本满足式(1)所示的正弦函数。

(1)

式中：T(d)为时程温度，℃；tm为年平均温度，℃；Ay为年温度振幅，℃；d为当前时间；d0为初始时间。

3.2.1 隧道进口监测温度

将隧道进口各个监测断面监测结果绘制成曲线图，如图5所示。并对隧道贯通前后数据进行拟合，统计见表2。

表2 贯通前后隧道进口衬砌表面空气温度变化

(a)监测断面1

针对隧道贯通前，以进洞距离x作为自变量，以进口各监测位置的年平均温度tm与年温度振幅Ay作为因变量进行函数拟合，得到式(2)和式(3)。其决定系数R2分别为0.929 4和0.958 0，均大于0.8，拟合效果较好。

tm(x)=-12.42e-x/451.99+13.17。

(2)

Ay(x)=12.02e-x/338.05+2.25。

(3)

针对隧道贯通后，以进洞距离x作为自变量，以进口各监测位置的年平均温度tm与年温度振幅Ay分别作为因变量进行函数拟合，得到式(4)和式(5)。其决定系数R2分别为0.941 4和0.920 3，均大于0.8，拟合效果较好。

tm(x)=-11.78e-x/551.77+12.24。

(4)

Ay(x)=11.67e-x/433.41+3.77。

(5)

3.2.2 隧道出口监测温度

将隧道出口各个监测断面监测数据绘制成曲线图，如图6所示。对隧道贯通前后数据分别进行拟合，统计见表3。

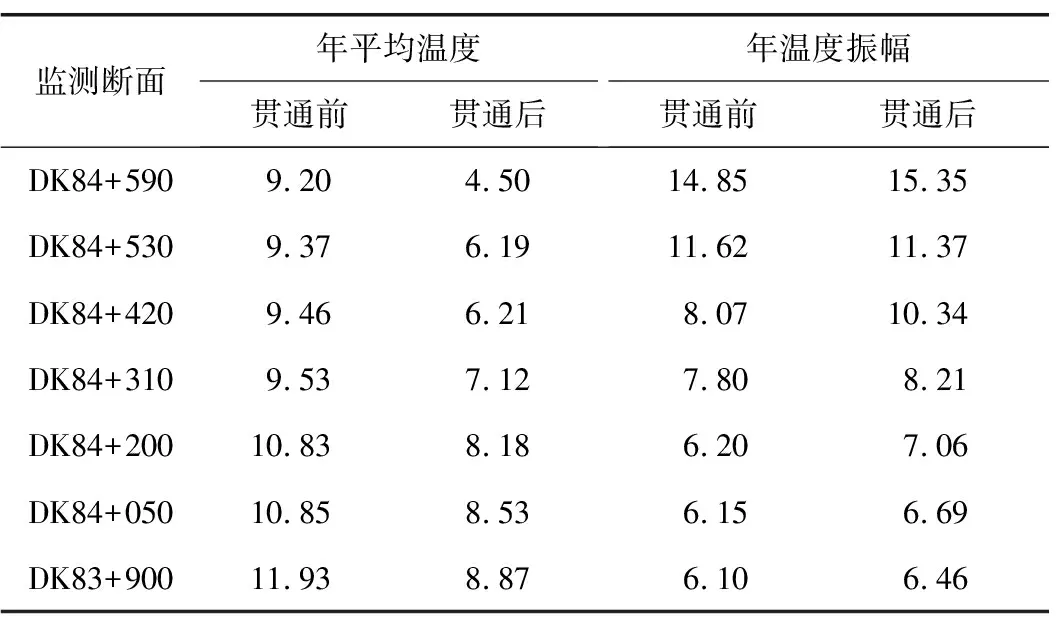
表3 隧道贯通前后出口衬砌表面空气温度函数变化

针对隧道贯通前，以进洞距离x作为自变量，以出口各监测位置的年平均温度tm与年温度振幅Ay分别作为因变量进行函数拟合，得到式(6)和式(7)。其决定系数R2分别为0.819 3和0.896 1，均大于0.8，拟合效果较好。

tm(x)=-3.79e-x/679.79+12.69。

(6)

Ay(x)=10.06e-x/240.86+4.34。

(7)

针对隧道贯通后，以进洞距离x作为自变量，以出口各监测位置的年平均温度tm与年温度振幅Ay分别作为因变量进行函数拟合，得到式(8)和式(9)。其决定系数R2分别为0.921 1和0.912 2，均大于0.8，拟合效果较好。

tm(x)=-6.38e-x/624.38+11.24。

(8)

Ay(x)=9.85e-x/301.27+4.68。

(9)

3.2.3 结果分析

由图5及图6可看出，随着进洞深度的增加，隧道进、出口的衬砌壁面空气温度，受洞外温度的影响逐渐下降，而受到隧道围岩温度的影响逐渐上升。具体表现为：随着进洞深度的增加，年平均温度上升，而年温度振幅减小。通过对比冬季和夏季洞外环境温度与洞内原始地温的差异，发现夏季洞外环境温度与洞内原始地温差异较小，而冬季各断面的温度差异相对夏季更大，且夏季各断面温度相当接近。

(a)监测断面1

通过进口与出口对比可以发现，随着进洞深度增加，出口的年平均温度增长幅度都较进口小。例如：进口贯通前，年平均温度增加了10.01 ℃，而出口仅增加了2.73 ℃。分析原因是由于出口的洞外温度相对进口的更高，随着进洞距离的增加，洞内温度都接近于原始围岩温度。

依托工程隧道的进口为直线段，出口为曲线段。受沿途阻力系数等因素的影响，出口断面的年温度振幅变化幅度较进口的小，出口断面的年温度振幅降低了8.75 ℃，而进口断面的年温度振幅降低了10.77 ℃。

结合表2及表3绘制贯通前后进出口最低温度距洞口距离变化规律曲线，如图7所示。

图7 进出口最低温度距洞口距离变化规律

隧道贯通前后隧道温度也出现明显变化，分析图5—7可知：隧道贯通前，洞内温度仅受其开挖侧洞外温度的影响；隧道贯通后，洞内温度受两侧洞外相对低温的共同作用，导致同一断面的年平均温度及年温度振幅分别减小、增大。隧道进口可能受冻害影响范围由距洞口约325 m增至约490 m，而隧道出口由距洞口约135 m增至约340 m。此外，贯通前后进口低温影响区都较出口的更长。

4 温度场模拟分析

本文采用Fluent软件建立流固耦合瞬态传热数值模型，并进一步探究隧道进口风速、温度等要素对温度场的影响。

4.1 模型建立

左右线隧道最小净距不大，约为28 m，两洞间的热量传递几乎可以忽略，故本文仅对其中1条隧道进行数值模拟。模型横截面为80 m×80 m的矩形，隧道断面参照设计图纸，隧道模拟长度设置为4 228 m，见图8。根据现场试验结果，围岩及衬砌等材料的热力学计算参数见表4，洞内空气计算参数见表5。

表4 热力学计算参数

表5 空气计算参数

(a)整体模型(单位: m) (b)网格划分

4.2 初始地温及边界条件

在Fluent模拟过程中，设置空气流入洞口为速度入口边界，并赋予相关温度及风速等参数；另一方面，设置空气流出洞口为自由出流边界。将计算得到的原始地温设置为围岩温度初始值。

根据隧道纵断面图，建立ANSYS二维平面模型进行地层初始温度计算，其分布云图见图9。为了便于UDF编译，对隧道进出口段的围岩温度进行函数拟合，其结果见式(10)及式(11)[16]。

图9 地层初始地温度场分布云图(单位：℃)

(10)

(11)

式(10)—(11)中:T为围岩温度；x为进洞深度。

4.3 曲线隧道纵向温度场分布规律

4.3.1 曲线隧道纵向温度场分布规律

结合隧址区温度监测，隧道进口风温以最冷月平均气温为标准，设置为-15 ℃，同时设置进口风速为2 m/s，单向通风持续60 d。为显现曲线隧道温度场的分布特点，对相同工况下的曲线隧道和直线隧道进行对比分析。曲线隧道及直线隧道壁面温度及衬砌背后温度的纵向温度场分布规律如图10所示。

图10 隧道纵向温度场分布规律

由图10分析可知：对于寒区隧道，隧道洞身回温现象明显，且邻近隧道洞口的洞内温度受外界环境变化影响明显大于洞身段。隧道壁面温度及衬砌背后温度沿纵向分布呈“两端洞口低、洞身相对高”的偏锋型分布规律，即在进口段温度急剧上升，而后进入缓慢上升阶段并开始趋于稳定，接近出口段时温度又急剧下降，总体上与现场实测温度较为吻合。

对比曲线隧道和直线隧道的温度场分布规律，由于金家庄螺旋隧道在前612 m为直线段，故2种隧道温度场分布规律在该区间内吻合度较高。进入曲线段后，曲线隧道的内外径温度开始产生差异，相较于直线隧道，曲线隧道的外径侧升温速度加快，致使在任一进洞深度处，曲线隧道的外径侧温度较直线隧道温度更高，而内径侧温度反之。但在经过约500 m的温度分化过程后，隧道内外径的温度与直线段的温度差不再进一步扩大，曲线隧道内外径的温度变化速率与直线段基本一致。内外径的温度值基于直线隧道的温度值基本上呈现对称现象。

4.3.2 分布规律原因分析

为对比直线段与曲线段的差异，分别取隧道进口600 m及800 m处断面的速度云图进行比较，见图11。由图可知：处于隧道直线段进口600 m断面的风速云图与温度场一致，均呈对称分布；处于曲线段进口800 m处断面的风速云图中其外径侧风速大于内径侧。

(a)进口600 m处

风速云图与温度场具有一致性，为进一步分析该现象出现的原因，选取隧道曲线段距进口612(直线与曲线段分界处)、800、1 000、1 200、1 600、2 400、3 200、4 000 m断面的风速绘制成图12。

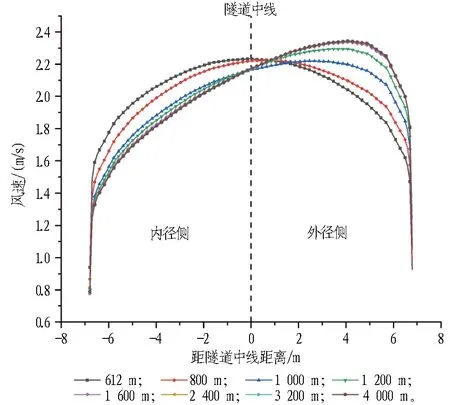
图12 隧道不同断面风速分布规律

由于隧道特殊的螺旋结构，隧道内风流在经过直线段与曲线段交界处时，在惯性作用下，流体仍按原方向流动，更多的风流汇聚到外径侧，致使单位时间内外径侧通过的空气增多(如图13所示)，从而出现隧道外径一侧的空气流速相较于内径一侧更大的现象。此外，由于同一断面处外径侧空气流速更快，空气与衬砌围岩换热时间更短，洞外的低温空气更易进入隧道更深处。因此，在曲线段隧道同一断面位置，出现了“空气流场外径侧较内径侧流速大、温度场外径侧较内径侧温度低”的分叉现象。

图13 隧道直线与曲线段交界处流场示意图

另外，隧道衬砌对流换热系数受其表面附近流体流速影响，隧道外径侧衬砌与空气的对流换热系数大于内侧。结合式(12)，隧道外径侧流体温度更低、对流换热系数更大，外径侧单位时间内交换的热量更多，导致衬砌背后温度相较于内径侧更低。因此，在隧道衬砌背后温度场也出现了“外径侧较内径侧温度低”的分叉现象。

q=h(Tw-Tf)。

(12)

式中：q为热量;Tw、Tf分别为衬砌表面和流体的温度；h为对流换热系数。

由于螺旋隧道的结构特点，在寒区螺旋隧道的保温设计过程中，应以较不利工况(温度较低值)，即以隧道外径侧温度场作为参考。

4.4 进口风速对温度场的影响

采用控制变量法，通过改变自然风速设置工况，设置自然风速为1、2、3、4 m/s 4个工况。洞口进风温度设为-15 ℃，计算单向通风60 d的瞬态温度场。隧道壁面及衬砌背后纵向温度场分布规律分别如图14和图15所示。

图14 不同进口风速衬砌壁面纵向温度场分布

图15 不同进口风速衬砌背后纵向温度场分布

对比分析不同风速下的温度纵向变化规律，不同进口风速的曲线隧道温度场分布规律大体一致。风速越大，隧道进出口产生的风墙压差越大，使得进口的低温空气更易进入隧道内部，导致洞内温度受洞外温度的影响更大。即相同断面处温度更低、纵向上冻结长度更长，需要敷设长度更长的保温层以预防冻害现象。

4.5 进口风温对温度场的影响

采用控制变量法，通过改变自然风温设置工况，设置自然风温为-10、-15、-20、-25 ℃ 4个工况。设置进口风速为2 m/s，计算单向通风60 d的瞬态温度。隧道壁面及衬砌背后纵向温度场分布规律分别如图16和图17所示。

图16 不同进口风温衬砌壁面纵向温度场分布

图17 不同进口风温衬砌背后纵向温度场分布

对比分析不同进口风温下的温度纵向变化规律，不同进口风温的曲线隧道温度场分布规律大体一致。洞外温度越低，相同进洞深度位置处低温空气与隧道的热交换越多，对洞内温度场的影响越大。即相同断面处温度更低，纵向上冻结长度更长，需要敷设长度更长的保温层以预防冻害现象。图16—17显示，进口风温对隧道纵向温度场的影响是线性的，进口风温每降低5 ℃，隧道整体纵向温度场则降低约2.5 ℃。

4.6 保温层敷设长度

保温层是预防寒区隧道冻害的一项重要措施。本文以进口风温及进口风速为变量，将进口风速1、2、3、4 m/s与风温-10、-15、-20、-25 ℃两两组合，共设计16个工况探究寒区保温层的敷设长度。基于施工角度考虑，本文以更不利的敷设长度作为建议长度，故以衬砌背后温度是否达到0 ℃为标准，将隧道外径侧的衬砌背后冻结长度作为保温层的敷设长度。统计各个工况的数据结果绘制成表6。

表6 不同进口风速风温的隧道保温层长度

将表6统计结果进行拟合分析，获得以进口风温及进口风速为变量的保温层长度计算公式(拟合度达0.903 7)：

(13)

式中：l为保温层敷设长度，m；v为进口风速，m/s；T为进口风温，℃。

此外，为更直观地反映进口风温风速与保温层长度的关系，绘制进口风温风速与保温层长度关系三维效果图，如图18所示。

图18 进口风温、风速与保温层长度关系三维效果图

将金家庄螺旋隧道的设计风速及洞外最冷月最低气温代入式(13)中，计算该隧道进口的保温层长度理论上至少为1 239 m，可为保温层长度设计提供参考。

5 结论与讨论

依托河北金家庄特长螺旋隧道，结合现场实测的洞口气象数据进行模拟分析，探究寒区螺旋隧道温度场的分布规律及影响因素，得到以下结论。

1)依托工程隧道进出口的衬砌壁面空气温度随着进洞深度的增加，受洞外温度及围岩温度的影响，年平均温度逐渐上升，而年温度振幅变小。

2)由于隧道贯通，洞内温度受两侧洞外相对低温的共同作用，相较于贯通前，同一断面处的年平均温度减小，而年温度振幅则出现增大的现象。

3)金家庄特长螺旋纵向温度场整体上呈偏锋型分布，在直线段温度场分布规律与同条件下的直线隧道一致，从曲线段开始内外径温度曲线发生分叉，数值上内外径的温度值基于直线隧道的温度值呈现对称现象。

4)进口风速越大、进口风温越低，隧道纵向上冻结长度更长，需要敷设长度更长的保温层，通过计算，金家特长螺旋隧道进口的保温层长度理论上至少为1 239 m。

本文仅对依托工程下的隧道几何特征进行分析，后续将进一步探究不同曲线形式下的隧道温度场变化规律，以保证在寒区螺旋隧道保温层设计的适用性。此外，还将增设隧道直曲变化处温度监测，深入探究隧道直曲变化处的温度变化规律。