园区综合能源系统低碳经济双层联合优化
谭玉华,李 臣,张 迁,陈奇林,余 诺
(1.上海理工大学机械工程学院,上海 200093;2.安徽省教育厅能源互联网工程技术研究中心,安徽 芜湖 241000)
0 引言
在“碳达峰”“碳中和”目标背景下,探索更高效、清洁、经济的综合能源利用方法及其系统规划运行模式具有重要的理论与现实意义[1-2]。合理的规划运行方案是保障综合能源系统(integrated energy system,IES)发挥运营效能的必要前提。
目前,国内外学者在园区综合能源系统规划运行方面开展了相关研究并取得了一定成果。文献[3]建立了含热电联产机组、燃气机组和制冷装置的园区综合能源系统组合优化模型,以系统可靠性与经济性为目标对系统内各设备的安装容量进行规划,但并未考虑系统运行期间的优化策略。文献[4]综合考虑规划层面的投资成本和运行层面的运行成本,从经济性的角度基于混合整数线性规划方法对园区综合能源系统的优化配置进行研究。文献[5]在经济性的基础上进一步考虑可靠性指标,通过双层协同优化方法对区域综合能源系统的设备配置方案和日运行策略进行优化。但随着双碳目标的提出,只考虑经济性、能效性和可靠性等指标为优化目标的园区综合能源系统规划运行已难以满足当代社会的发展需求。除上述指标以外,还必须考虑环境污染、碳排放等环保性指标并合理衡量不同指标之间的矛盾与制约关系[6]。
为此,本文提出一种园区综合能源系统物理模型,采用规划-运行双层迭代优化方法对系统的经济性和环保性作多目标协同优化,应用非精英策略的非支配排序遗传算法(non-dominated sorting genetic algorithm,NSGA-II)求解得到低碳经济的最优方案,并对结果进行了对比分析。
1 园区综合能源系统模型
综合能源系统是指在规划、建设和运行等阶段,通过对能源的生产、运输、分配、转化、存储、消费等环节进行有机协同优化后形成的多能源产供销一体化系统[7]。其中包括直接面向终端能源用户的园区综合能源系统。园区综合能源系统是一种小型系统,通常根据能量梯级利用原则对多种分布式能源设备进行综合优化配置,从而将风能、光能、电能和天然气等多种形式的能源转化为冷、热、电等负荷供用户使用。
本文提出的园区综合能源系统结构如图1所示。
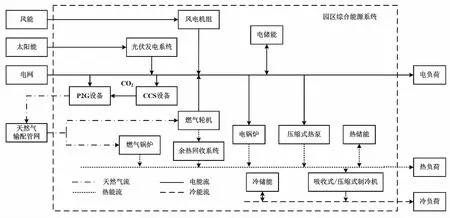
图1 园区综合能源系统结构示意图
园区综合能源系统中:电负荷需求主要由风电机组、光伏发电系统、燃气轮机、电储能设备和电网电力满足;热负荷需求主要由燃气锅炉、余热回收系统、压缩式热泵、电锅炉和热储能设备满足;所产生的热量通过驱动吸收式/压缩式制冷机等空调制冷装置进一步满足冷负荷需求。相关研究表明[8-11],电转气(power to gas,P2G)技术可以将水分解为O2和H2,而碳捕集与封存(carbon capture and storage,CCS)技术可以有效捕集各设备出力过程中产生的CO2。将P2G技术和CCS技术结合之后,可以利用其中的H2和CO2合成CH4,并将CH4作为能源燃料再次使用,从而在降低碳排放量的同时减少运行燃料成本,并兼顾系统的经济性和环保性。为了减少碳排放,系统还配置了P2G设备和CCS设备。其中:P2G设备消耗电能产生O2和H2;CCS设备捕集各设备出力过程中产生的CO2。产生的H2和捕集的CO2进一步生成CH4作为天然气燃料循环使用。
1.1 供热设备模型
园区综合能源系统采用燃气轮机和余热回收系统作为热电联产(combined heat and power,CHP)机组。该机组通过消耗天然气产生电能和热能。其数学模型为:
(1)
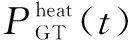
由于系统由CHP机组首先提供电负荷与热负荷,所以当其不能满足热负荷需求时,由燃气锅炉、电锅炉和热泵来提供热负荷。其数学模型为:
(2)
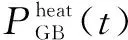
(3)
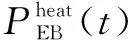
(4)
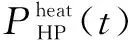
1.2 供电设备模型
园区综合能源系统的电负荷由CHP机组、风电机组和光伏发电系统提供,并在出力不足以供应负荷需求时向电网购电。设备的数学模型为:
(5)
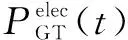
0≤PWT,k(t)≤uWT,k
(6)
式中:PWT,k(t)为第k台风电机组在t时刻的实际出力,kW;uWT,k为第k台风电机组的安装容量,kW。
0≤PPV,r(t)≤uPV,r
(7)
式中:PPV,r(t)为第r台光伏设备在t时刻的实际出力,kW;uPV,r为第r台光伏设备的安装容量,kW。
1.3 供冷设备模型
园区综合能源系统的冷负荷由吸收式制冷机和压缩式制冷机分别转换热能和电能获得。设备的数学模型为:
(8)
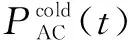
(9)
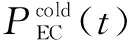
1.4 储能设备模型
园区综合能源内的储能设备可以在提升系统运行经济性的同时提高系统灵活性。本文对储能设备的建模是基于一种广义储能动态的通用模型。该模型中:状态变量为储存的能量;控制变量为充放能功率。经过典型日运行周期内各时段的递推,可以得到整个运行阶段的状态变化。递推表达式为:
Qs(t+Δt)=Qs(t)+Ps,in(t)Δt-Ps,out(t)Δt,∀k∈
{GCST,GHST,GBT},t∈{t1,t2,…,t24}
(10)
式中:Qs(t)为t时刻储能设备k储存的能量,kW·h;Ps,in(t)、Ps,out(t)分别为t时刻储能设备k的充、放能功率,kW;Δt为单个时段的时间尺度,h;GCST、GHST和GBT分别表示蓄冷罐、储热罐和蓄电池。
1.5 P2G和CCS模型
P2G设备消耗电能产生O2和H2。CCS设备捕集各设备出力过程中产生的CO2,产生的H2和捕集的CO2进一步生成CH4作为天然气燃料。P2G设备和CCS设备在运行过程中需要消耗电能,在合成天然气的过程中需要协同运行。其数学模型为:
PP2G(t)=αDP2G(t)
(11)
式中:PP2G(t)为P2G设备产出天然气的速率,m3/h;α为电-气转换系数;DP2G(t)为P2G设备消耗的电功率,kW。
DC(t)=βDP2G(t)
(12)
式中:DC(t)为P2G设备消耗对应电功率所需的CO2量,kg;β为P2G设备消耗电功率与对应CO2量的比例系数。
DCCS(t)=ωDC(t)
(13)
式中:DCCS(t)为CCS设备捕获CO2消耗的电功率,kW;ω为CCS设备捕获CO2的效率。
2 多目标优化模型及其求解算法
园区综合能源系统的规划运行联合优化问题是一个含多目标、多约束、多变量的混合整数非线性优化问题。不同的设备配置方案、运行方式均会影响系统的实际性能。本文以经济性和环保性为目标,对园区综合能源系统的配置方案和运行方案进行双层迭代优化。
综合能源系统双层优化模型如图2所示。
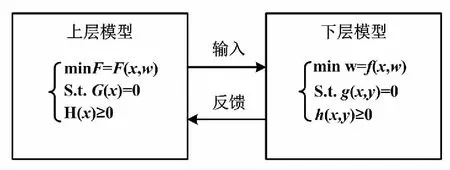
图2 综合能源系统双层优化模型
上层模型研究规划问题,以系统经济性指标和碳排放量指标为目标函数进行设备优化配置。优化后的配置方案作为已知条件传输给下层模型进行运行优化。下层模型研究运行优化问题,在给定配置方案条件下对系统的运行状态进行优化,以降低运行过程中的运行成本和碳排放量;同时,将优化结果反馈回上层进行总成本和总碳排放量的优化计算,通过循环迭代得到最优的设备配置方案和运行策略。
2.1 上层规划模型
上层规划模型是一个非线性多目标优化问题,优化变量是各类设备的装配组合,安装台数均为整数变量。规划目标是全生命周期总成本协同碳排放量最优。
2.1.1 目标函数
上层规划模型的目标函数由经济性目标Ctotal和碳排放量目标ζC两个相互独立的部分组成:
Ctotal=Cinv+Com+Cop+CC
(14)
式中:Cinv为系统的年化投资成本;Com为年设备维护成本;Cop为运营成本期望值;CC为所需要支付的碳交易费用。
(15)
式中:N为园区综合能源系统内的规划设备种类数;nv为类型为v的设备台数;μv为类型为v的设备单价,万元;rv为类型为v的设备折现率;yv为类型为v的设备使用寿命,年。
Com=δCinv
(16)
式中:δ为设备维护成本系数。
CC=τ(ζquota-ζactual)
(17)
式中:τ为单位碳交易价格,250元/t;ζquota为系统的碳排放配额;ζactual为系统实际碳排放量。
系统中产生单位电功率的碳排放权分配额取0.728 t/MWh,产生单位热功率的碳排放权分配额取0.102 t/GJ。
由于经济性目标为年总成本,所以碳排放目标也折算为年碳排放总额。
(18)
式中:ζCtotal为系统运行的年碳排放量;ζCseason为系统运行的季碳排放量。
2.1.2 约束条件
设备安装数量受实际地域条件限制,为:
(19)
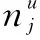
2.2 下层运行模型
下层运行模型是在上层优化配置方案确定的前提下对园区综合能源系统典型日各个时段的运行状态进行优化,也是非线性多目标优化问题。优化变量是各设备出力和储能状态,均为连续型变量。优化目标是典型日运行成本和碳排放量。一般而言,全年所有时段均需进行优化。但这会大大增加运行优化模型的变量总数和约束条件,使得模型难以求解。本文采用典型日的方法对下层运行优化模型进行构建,即根据当地的气候环境、资源禀赋和能量供需情况,将全年划分为几个典型日,并统计一年中不同典型日的累积天数,再以典型日为运行周期进行运行优化模型构建。
2.2.1 目标函数
运行成本包括系统的购电和购气费用,计算式为:
Cop=Cele+Cgas
(20)
式中:Cele、Cgas分别为系统的年购电费用和年购气费用。
(21)
式中:cele(t)为t时刻的电价,元/kWh;cgas(t)为t时刻的气价,元/m3;ρele(t)为t时刻的购电功率,kW;γgas(t)为t时刻的购气功率,m3;li为第i季典型日的年化代表天数。
系统的日碳排放量表达式为:
(22)
式中:aC、bC为CHP的碳排放系数;Hν为CHP出力热电能效比;εC为外部电网购电的碳排放当量因子;εC,g为燃气锅炉消耗天然气对应的碳排放系数;εC,h为吸收式制冷机消耗热量对应的碳排放系数;εC,e为压缩式制冷机、电锅炉和热泵消耗电力对应的碳排放系数。
2.2.2 约束条件
园区综合能源系统内多种能源通过各子系统进行汇集和分配,在运行阶段需满足以下各时刻的冷、热、电、气子系统能量平衡约束。
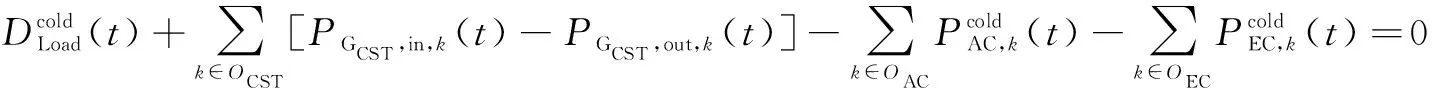
(23)
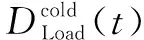
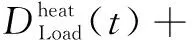
(24)

典型日t时刻热负荷需求由系统内制热设备产能、耗热设备耗能及热储能设备配合出力进行满足,以达到供需平衡。
(25)

典型日t时刻电负荷需求由系统内制电设备产能、耗电设备耗能及电储能设备配合出力进行满足,以达到供需平衡。
(26)
典型日t时刻天然气子系统内的设备产量与购入量之和等于消耗量。
各能量转换设备均需满足出力上下限约束,即:
0≤Pk(t)≤uk
(27)
式中:uk为能量转换设备k的容量上限。
2.3 模型求解算法
本文采用NSGA-II算法求解上、下层中的非线性多目标优化问题。NSGA-II算法是一种带有精英保留策略的非支配排序遗传算法,在多目标优化问题上具有较好的求解效果,可以通过迭代求出一组Pareto最优解集。
求解步骤如下。
①输入NSGA-II算法参数、设备参数、典型日负荷及可再生能源出力数据。
②上层模型根据初始条件产生个数满足约束条件的配置方案,并对其进行非支配排序,将排序结果传递至下层。
③下层模型依次对每种配置方案进行运行优化。每种配置方案对应生成数个设备出力方案及目标结果,并根据目标函数值进行非支配和拥挤度排序。
多目标双层优化模型求解流程如图3所示。
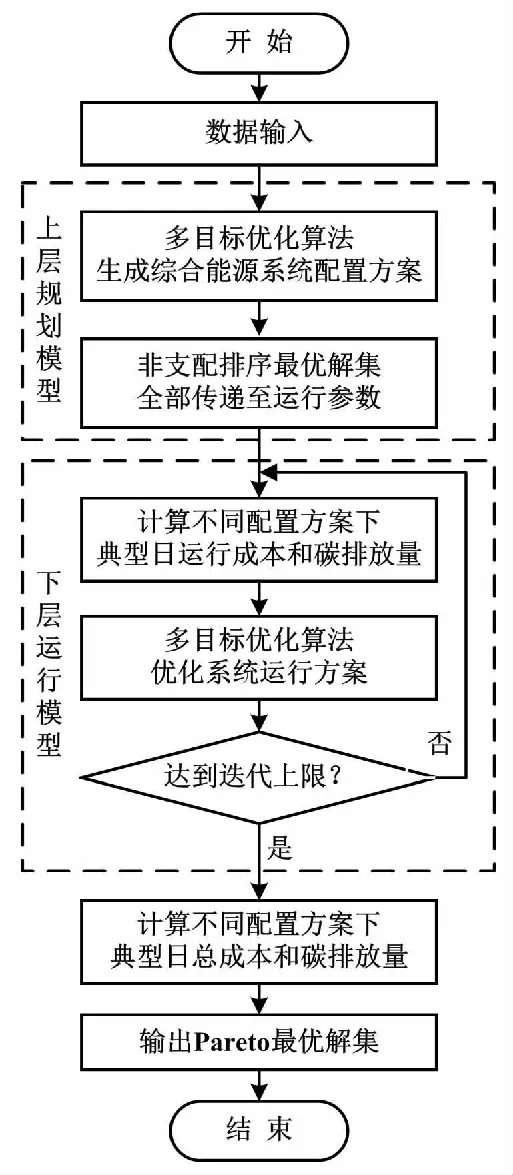
图3 多目标双层优化模型求解流程
④将下层模型的排序结果反馈至上层模型,计算相应配置方案的目标函数值。
⑤重复步骤③和步骤④,直至算法达到收敛条件。根据目标函数值对所有配置方案进行非支配排序,选取排名占优的非支配解集中的所有个体作为Pareto最优解集,输出结果。
3 算例分析
本文选取苏州某示范园区的综合能源系统作为具体算例,基于所提模型和算法对其进行规划-运行联合优化。系统内碳排放计量相关的算例参数[11]如表1所示。
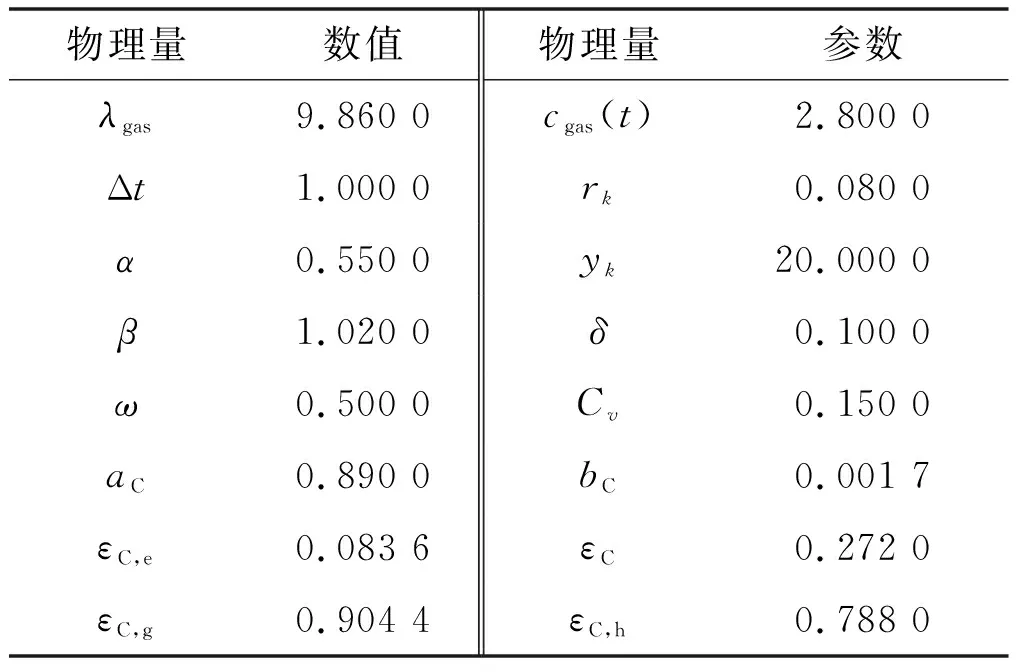
表1 算例参数
设备参数[12]如表2所示。

表2 设备参数
苏州某示范园区负荷、电价、可再生能源出力曲线[5]如图4所示。
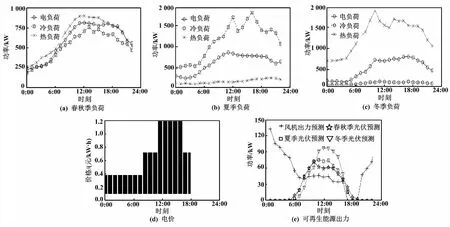
图4 负荷、电价、可再生能源出力曲线
基于本文所提方法,对苏州某示范园区进行规划运行联合优化。首先在上层模型随机生成若干种不同的园区综合能源系统配置方案,并按照目标函数初始期望值进行非支配排序;然后按照排序结果依次传入运行层模型进行计算;最后将下层输出结果反馈至上层,在反复迭代后完成多目标优化,得到一组Pareto最优解集。在解集中,各种配置方案之间无优劣之分,只在经济性和低碳性目标之间权重不同。
Pareto最优解集分布如图5所示。图5直观展示了经济性目标和低碳性目标间的关联性,从中选取典型方案进行分析。由于不同季节典型日内系统的冷、热、电负荷需求不同,所以在规划阶段需要考虑各类负荷的上限来配置设备。而在运行阶段,则需要针对不同季节典型日冷、热、电负荷的需求差异优化设备出力。
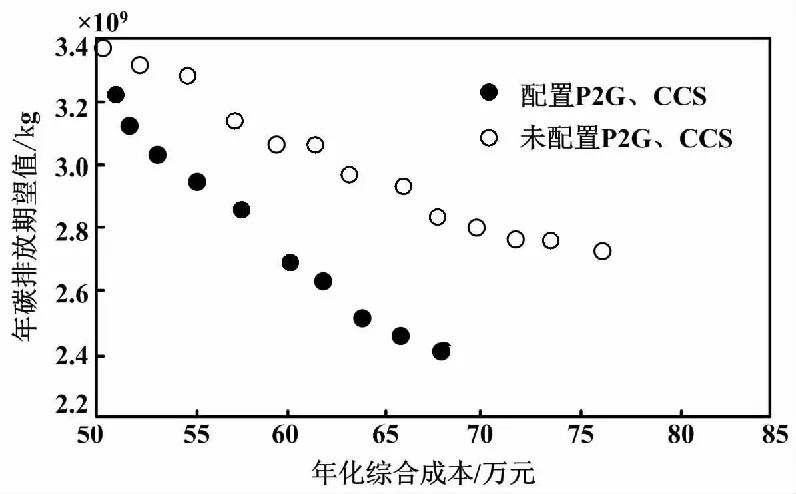
图5 Pareto最优解集分布图
此处选取方案1作为典型方案对设备出力优化结果进行分析。
IES典型配置方案如表3所示。
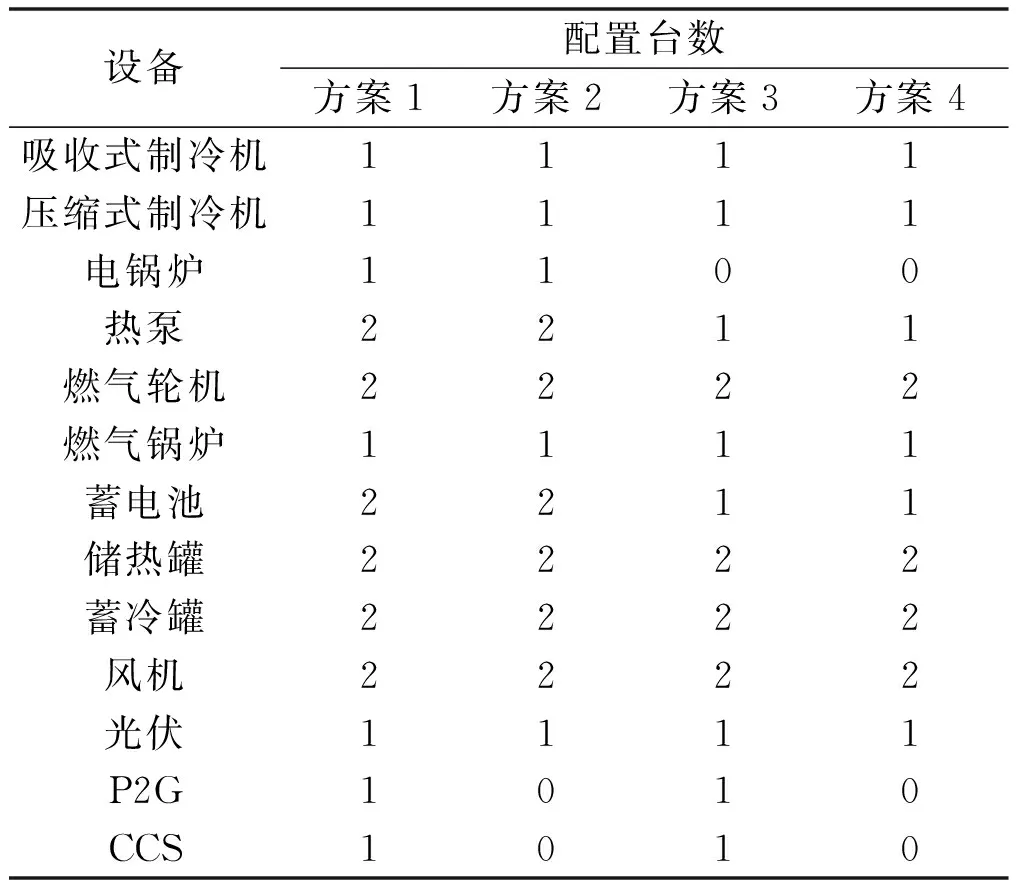
表3 IES典型配置方案
典型日最优运行方案如图6所示。
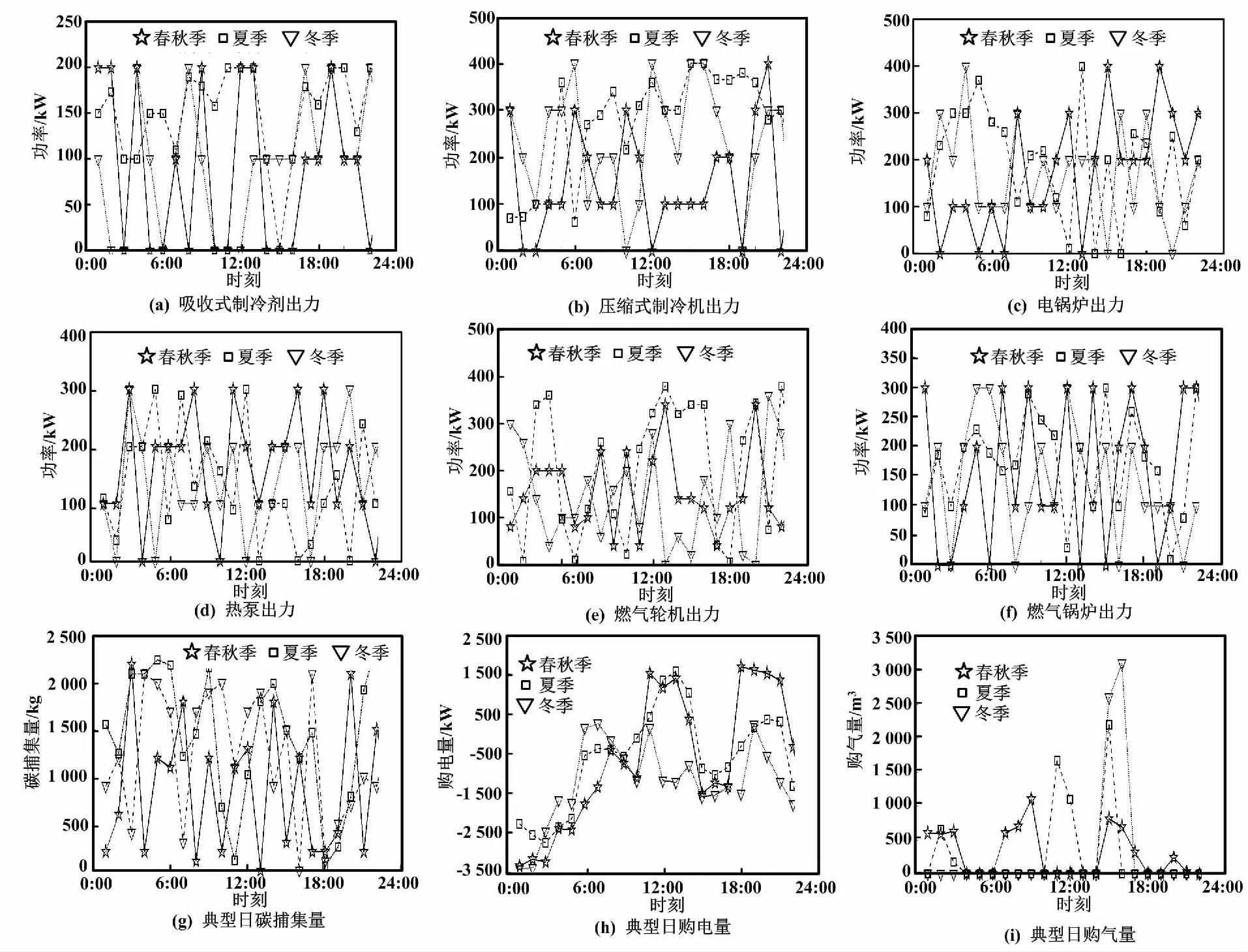
图6 典型日最优运行方案
图6(a)~图6(f)为不同季节典型日内各能量转换设备在各时刻的出力情况。图6(g)为碳捕集设备在不同季节典型日内各时刻碳捕集量。图6(h)和图6(i)分别为不同季节典型日内各时刻系统的购电量和天然气购入量。由图6可知,在夏季典型日内供热设备出力较少,而供冷设备出力较多;在冬季典型日内则是供热设备出力较多,供冷设备减少出力;在春秋季典型日内各设备出力曲线较为集中,各设备出力较为均衡,与其冷、热负荷需求差异较小有关。不同典型日内购电量曲线走势基本一致,在用电高峰时段从电网购入,在低谷阶段售出多余电能。而由于配置了P2G设备,天然气购入量持续较少,在碳捕集量较低的时段,天然气购入量有所升高,对应了P2G和CCS设备的出力耦合情况。
根据上层模型确定的配置方案及下层模型优化的运行阶段设备出力情况,可计算典型方案的年平均成本和年碳排放量。
性能指标结果如表4所示。
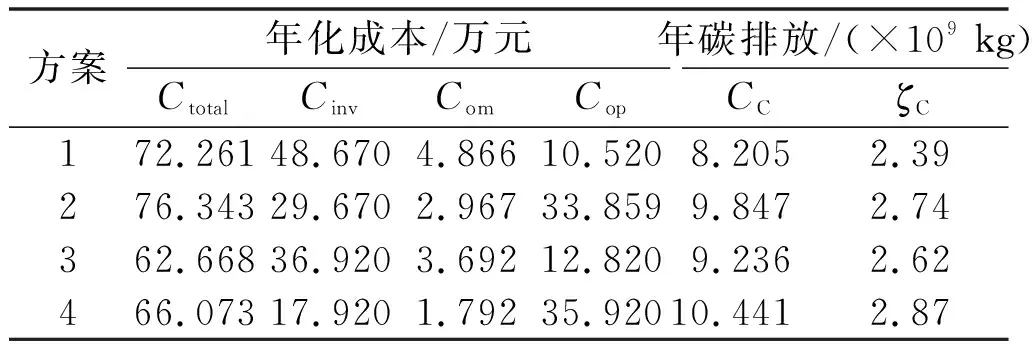
表4 性能指标结果
由表4可知,方案1、方案3与方案2、方案4相比,前二者的碳排放量明显降低。其中,方案1比方案2多降低12.8%的碳排放量、方案3比方案4多降低8.7%的碳排放量。这表明,配置了P2G和CCS设备的系统,在降低碳排放方面效果显著。在经济性方面,配置了P2G和CCS设备的系统投资成本增加,但运行成本和碳交易成本都有所下降,总成本节省约5%。这表明,在设备寿命周期内,配置P2G及CCS设备不仅可大幅减少系统碳排放量,还可实现总成本的降低,兼顾了经济性与低碳性。
4 结论
在双碳目标背景下,针对现有研究中的不足,本文考虑在园区内引入P2G和CCS设备,提出了一种园区综合能源系统物理模型。在对系统内设备及能量转换关系进行数学建模的基础上,充分考虑系统不同配置方案、运行策略、季节变化和日内时序变化影响。算例结合规划-运行两个层面,对于系统的经济性和碳排放量,采用双层迭代优化方法对其进行综合衡量和多目标协同优化,并采用NSGA-II算法求出系统优化配置方案和运行方案的Pareto最优解集。该解集可以进行直观展示和量化分析,为规划运行人员提供理论依据,帮助他们根据具体需求进行侧重选择并作出切合实际的最优决策。仿真算例及不同方案对比分析结果表明,所提系统模型在规划年限平均总成本相近时可有效降低系统碳排放量,同时也验证了所提双层规划运行模型及其算法的有效性。
————不可再生能源

