基于FIAS的初中数学课堂教学行为研究

文/湖北大学师范学院 郭俊宏

弗兰德斯互动分析法（Flanders interaction analysis system，FIAS）是美国明尼苏达大学的学者弗兰德在20世纪60年代所提出的一种探索课堂教学本质和教学规律的分析技术，用于记录和分析教学情境中师生语言互动的情况。弗兰德斯认为，在一堂课的所有教学行为中，语言行为大约占80%，是一种主要的课堂教学行为，因此对课堂内的师生语言互动行为进行分析是评价一堂课的最好方法。自20世纪80年代，我国学者孙祖夏等通过翻译国外文献首次将其引进后，我国大量教育研究者用其改进的方法进行教学研究。于洁等借助该系统，对高中地理课堂教学行为进行研究，并根据分析结果提出转变教师主宰角色，注重培养学生主观能动性等教学建议，鲁杰等利用该方法对一堂探究式化学课进行分析，从而促进探究式学习的发展和完善。

传统的弗兰德斯互动分析系统使用10项策略形式记录课堂互动过程。该编码系统对课堂行为的分析比较单一，仅仅关注到师生之间的语言互动行为。同时，编码的类别涵盖内容宽泛，区分时较容易出现主观判断导致分类误差。对此，我国相关教育研究者在各个维度对其进行改进：黄钟河等依据聋校课堂的特点修订弗兰德斯互动分析系统，采用矩阵分析、曲线分析等方法探讨聋校语文课堂教学师生言语行为互动特征；熊旭萍等开发了基于事件记录的弗兰德斯互动分析系统（ERFIAS）；李海伟等提出一种改进型弗兰德斯分析法，并基于的中小学课堂数据，增加了师生使用信息化设备的教学行为，在保持原弗兰德斯分析系统教学分析方式不变的前提下，弥补了传统弗兰德斯分析法在信息化教育背景中的缺陷与不足。鉴于此，本研究将2018年部级优课——“矩形中的折叠问题”与弗兰德斯互动分析系统相结合，基于改进后的编码系统评价初中数学课堂中师生言语互动行为，采用观察记录、矩阵分析、比率分析、曲线分析等方法，对课堂教学行为进行科学评估，并提出优化教学行为的改进建议。

一、弗兰德斯互动分析系统

弗兰德斯互动分析法包括三部分：一是描述课堂互动行为的编码系统；二是用于观察和记录编码的规定标准；三是用于显示数据，进行分析，实现研究目标的迁移矩阵。张海认为，该方法比较简单易于掌握，而且容易进行中立、客观地分析、记录和评价，具有强烈的结构化、定量化的特点，大大简化了课堂教学研究过程的复杂性，同时又提高了观察记录的科学性和准确性，成为半个世纪以来最有影响力的一种课堂观察技术，被广泛应用于各国中小学以及幼儿园的课堂研究中。

1.描述课堂互动行为的编码系统

传统的弗兰德斯互动分析系统将课堂教学行为划分为10类进行编码，但本文结合课堂教学的实际情况，认为学生在课堂中的学生自主讨论也属于学生语言，因此新增“学生自主讨论”为学生语言。同时，对于编码的类别涵盖内容宽泛，区分时较容易出现主观判断导致分类误差的问题，本文根据实际课堂情况在改进编码系统中进行了适当调整具体见下页表。

2.课堂观察记录

课堂观察记录表是研究课堂师生互动的一种最常见的方法。但全面的逐语记录常常会产生很大的工作量，而结构化的记录又可能失去很多教学细节信息。在课堂教学研究中，研究者每隔3秒按照弗兰德斯互动分析编码系统记录教学中的行为编码，并将其记录到弗兰德斯课堂观察记录表中，表中横行记录一分钟内每隔3秒行为编码，纵行表示所研究课程的总时长。课堂观察时，先记录第1横行，再记录第2横行，依次向下。一节课按照40-50分钟计算，大约有800-1000个编码，在此过程中容易出现人为误差。为了数据记录的科学性，应该尽量采用录音或录像方式对课堂教学过程进行保存，通过课后回放来记录编码，并且由两个人对同一段教学过程进行记录并对比编码差异，若编码差异较大则需邀请更具有经验的第三人进行编码。

3.构建弗兰德斯互动分析矩阵

将前后两个动作编码相连构成一个组合数据，一般称为“序对”，整堂课的课堂观察记录表通过编码的序对记录可构建分析矩阵。具体方法如下：首先将课堂观察记录表中的各行为编码记录为序对。例：师生言语互动行为的编码依次为6、8、6、5、5、1，将前后两个动作编码相连得：6-8、8-6、6-5、5-5、5-1。其次，计算各序对的个数，并填入分析矩阵表中的对应位置。最后将分析矩阵各行各列的值分别相加得到总计值。

弗兰德斯互动分析改进编码系统表

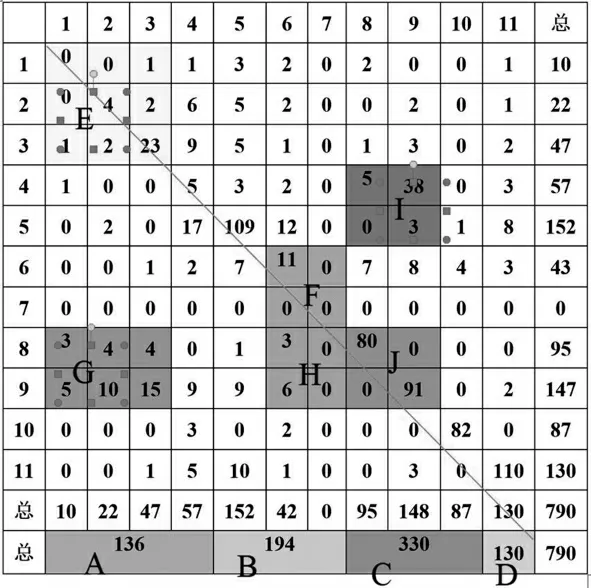
图1初中数学教学视频的语言互动分析矩阵

二、初中数学课堂教学行为分析

1.弗兰德斯语言互动矩阵解析

根据课堂记录的编码数据构建弗兰德斯互动分析矩阵，具体见图1。该语言互动分析矩阵中：A区域为136个，表示教师间接作用；B区域为194个，表示教师直接作用；C区域为243个，表示学生言语数量；D区域为130个，表示学生自主学习与课堂上暂时性的沉默；E区域序对数量为33，占比4.18%，该区域表示教师的积极语言行为，也称为积极整合格，该区域内的数字越大说明师生间的情感越融洽；F区域序对数量为11，占比1.39%，（6，6）占比过大，教师给予了学生冗长的指令，体现出教师的引导作用；G区域数量41，占比5.19%，H区域数量9，占比1.14%，表明教师在整个教学过程中中止学生说话的情况较少，体现了教师和学生能平等交流，呈现出和谐的氛围；I区域表示师生一问一答，数量46，占5.82%；J区域占21.65%，有171次，J区域占比很大，同时C区域占比较高，说明学生有很多的回答机会，体现了该课堂氛围活跃，学生能够跟紧老师的步伐积极回答问题，体现了课堂的活跃性。

根据弗兰德斯互动分析法，分析矩阵中对角线经过的各单元格为稳态格，位于稳态格的编码表示某种言语行为持续时间超过3秒，从上表的稳态格比率数据可以知道，（11-11）课堂上学生自主学习与（5-5）教师连续讲授的话语所占比率最高，其次是学生连续发言。由此说明在这一节课里，师生间的积极互动比较稳定，教师注重学生的沟通，而且在讲授中善于运用启发式的教学形式对学生的学习进行引导，充分调动学生参与课堂的积极性。

2.弗兰德斯语言互动比率解析

课堂结构分析。具体课堂教学中的言语行为存在巨大差异，不同学科、不同课程、不同教学风格必然导致言语互动行为的不同，因此需要具体问题具体分析。对课堂教学结构的分析可以判断课堂结构是否合理，是否达到最优化，而在教学实践中，课堂结构的优化能促进教学目标的完成和教学质量的提升。该课堂的课堂结构为教师言语占比41.77%，学生言语占比41.77%，学生自主学习占比16.46%。可以看出，教师言语比重低于学生言语加上学生自主学习，这说明该教师注重对学生的引导以及学生的自我思考，学生讨论积极性高，体现学生上课兴致高，对老师的教学给予肯定。

特征序对分析。相似特征序对的频数与比例可以反映出教师某些突出的教学行为特征。出现频次较多的特征序对代表了教师常有的一些教学行为，很多教师共有的序对也许说明了这些教师的共性特征。同一科教师经常出现相似序对，或许说明了这个科目教学的某些共同特点。在本课程中，序对（11-11）出现的频次为110次，占比超过13%，说明学生拥有足够的时间进行思考，有利于学生思维能力的培养；（5，5）出现的频次为109次，说明该教师持续讲述时间较长；（4，9）出现的频次为38，表明本次课堂教学中师生之间交流氛围融洽，学生能够积极主动回应教师。

3.课堂教学行为曲线解析

对课堂观察记录表或矩阵分析的一些结果可以进行曲线图形的分析，它能够更直观和形象地展示教学过程中的言语行为变化。除了直观之外，曲线图还有一大优势，可以考察连续的多个编码的分布特点。如图2所示，从曲线可以看出，教师语言行为占比超过或接近80%的时间点或时间段共有6次，但并未出现持续2分钟以上的现象。在37-39分钟中，教师语言出现空白，且同时学生语言也未出现，通过观看教学视频可得，此时课堂处于学生自主学习阶段，教师在教室内走动。学生言语行为占比超过50%的有14次，并且多次占比高达100%，说明该课堂出现学生的持续言语行为的次数较多。从曲线图中可以看出，学生言语行为占据主要地位，其次是教师言语行为，“教师讲，学生答”的模式贯穿整节课。

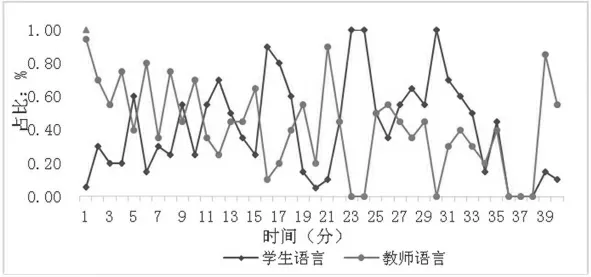
图2师生语言比率动态特征

三、总结

通过弗兰德斯互动分析系统对该节初中数学课程的编码、统计与分析，课堂教学中教师和学生间平等和谐，有良好的氛围、互动性强；教师中止学生说话的情况较少，且教师的教学风格积极，课堂氛围也积极活跃；教师善于利用启发性教学，通过提问来引发学生思考；教师提问时间短，提问方式恰当，充分发挥问题的价值，吸引同学们主动参与；整堂课呈现出以教师为主导，学生为主体的双主教学模式，尤其是学生积极讨论，体现学生上课兴致高，对老师的教学给予肯定。但是在该课堂中教师的间接教学比重小于直接教学，这种教学模式更适合小学的数学教学，对于初中数学而言，间接教学更能促进学生思维能力的发展。

课堂教学从根本上说是一种师生对话实践的过程。在本次基于弗兰德斯互动分析系统的初中数学课堂教学行为研究中发现，作为一种研究方法，它存在以下局限性：第一，忽视了非言语信息的重要性，课堂的研究对象和范围较小。随着学习环境的变革发展，各种教学媒体层出不穷，各种教学媒体的使用对教学的帮助也是不言而喻的，忽视信息化媒体对教学的作用将难以发掘教学过程中多维度的评价。第二，编码录入环节较容易出现人为误差。课堂的授课时间较长，特征序对数量庞大，人为录入编码的过程中每隔3秒对师生言语互动行为进行分析判断，这对记录者有极高的注意力要求，并且三秒录入一次的方法，打破了语言的整体性，增加了判断的主观性。第三，编码系统涵盖内容宽泛，区分度较低。编码系统对教师和学生的行为分类不够具体，有的行为在十种类型中存在争议。第四，难以追湖到教师具体语言，不利于教师反思与改进。