基于稳定经济模型预测控制的集群电动汽车辅助电网调频控制策略

余 洋 张瑞丰 陆文韬 米增强 蔡新雷

基于稳定经济模型预测控制的集群电动汽车辅助电网调频控制策略

余 洋1,2张瑞丰1,2陆文韬1,2米增强1,2蔡新雷3

（1. 新能源电力系统国家重点实验室（华北电力大学（保定）） 保定 071003 2. 河北省分布式储能与微网重点实验室（华北电力大学（保定）） 保定 071003 3. 广东电网有限责任公司电力调度控制中心 广州 510600）

针对电动汽车（EV）聚合建模忽略单体差异以及EV辅助电网调频难以兼顾经济性与稳定性等问题，该文首先，考虑电池容量差异，基于马尔科夫链理论提出了EV动态演化过程转移概率计算方法，推导了关于荷电状态的转移概率分布函数，构建了EV聚合模型，并建立了EV参与的两区域互联系统联合调频控制模型；然后，提出了基于稳定经济模型预测控制的双模态集群EV辅助电网调频控制策略，模态1通过经济模型预测控制降低调节成本，模态2利用辅助控制器确保系统稳定性；最后，通过仿真算例表明，聚合模型具有较高精度，控制策略能够优化协调各资源出力，在维持系统频率稳定的基础上，改善了频率调节过程中系统的经济性。

电动汽车 转移概率 聚合模型 负荷频率控制 稳定经济模型预测控制

0 引言

作为缓解能源和环境问题的新思路，电动汽车（Electric Vehicles, EV）移动储能技术受到了广泛关注。截至2020年底，我国已建成世界上充电设施最多、辐射面积最广、服务车辆最全的充电设施体系。预计至2030年，我国EV总容量将到达57亿kW·h[1]。以火电机组为主的传统调频手段难以满足新能源电力系统的调频需求。借助车电互联技术，充分利用EV电池的储能和快速响应特性，合理调控集群电动汽车（Aggregate Electric Vehicles, AEVs）充放电行为，已成为缓解电网调频压力的新途径[2]。EV分布广、数量多、单台车功率小，以聚合的形式更易参与电网调控。不过大规模EV的无序集聚，其充电负荷反而会加大峰谷差、降低电能质量，甚至对系统安全稳定运行造成负面影响[3-4]。因此，精确的聚合模型以及有效的联合调频策略是AEVs参与电网调频的两大关键技术[5]。

针对AEVs的聚合建模问题，文献[6]设计了基于对流方程的双线性聚合模型，并验证了聚合模型在新能源消纳和频率调节等方面的可行性；文献[7]借鉴温控负荷聚合建模思路，建立了AEVs的双线性可控充电模型，通过与直接聚合功率的对比验证了模型的有效性；文献[8]则综合考虑EV充电、放电、闲置三种状态，拓宽了AEVs的可调功率范围，同时利用Lax-Wendroff的二阶离散方法得到了更为精确且易于控制的线性聚合模型。然而，上述模型皆以聚合同质单体为假设，忽略了个体之间的差异性，导致建模的准确度不高。而基于马尔科夫链的建模方法能够通过概率密度函数表征单体之间的差异，利用转移概率构建聚合模型，如文献[9]阐述了温控负荷的马尔科夫性，提出了基于马尔科夫链计及热容异质性的温控负荷聚合建模方法。只是相较于温控负荷的温度变化周期，EV的荷电状态（State of Charge, SOC）变化周期要长得多，同样建模精度下对AEVs模型维数要求更高。故在考虑个体差异和保证建模精度等要求下，基于马尔科夫链的AEVs聚合建模还有待深入研究。

对于EV参与系统调频的研究已成为重要议题，文献[10]分析了EV荷源二重特性，建立了静态频率特性模型，证明了AEVs参与调频的可行性。文献[11]考虑SOC和出行需求建立了AEVs参与调频的充放电模式，但文中忽略了SOC的随机性对调频特性的影响。传统电力系统负荷频率控制以PID控制为主，但受控制参数数量多和系统状态约束动态变化等因素影响，PID控制性能偏弱[10]。模型预测控制（Model Predictive Control, MPC）综合考虑了输入、输出以及状态变量约束，可通过在线滚动实现对复杂多变量系统的优化控制。文献[12]利用MPC实现了AEVs对于调频指令的跟踪，文献[13]提出了基于MPC的风储联合调频策略，兼顾风储的实际约束，既平抑了风电波动又提高了系统调频性能；文献[14]提出了增量MPC的火光储协调优化频率控制方法，改善了混合发电系统的频率调节特性。不过上述文献均未考虑调频资源出力的经济优化分配，也未涉及AEVs与传统机组的联合调频，且普通MPC难以同时满足经济性与稳定性。为此，文献[15-16]提出了兼顾经济性和稳定性的双层MPC架构，上层用于各调频资源间的经济功率优化分配，下层实现频率动态控制，同时完成对上层经济最优点的跟踪。不过双层MPC架构忽略了下层控制过程的经济性，难以实现调控过程的全局最优。

综上所述，本文将基于马尔科夫链理论提出EV动态演化过程转移概率计算方法，推导EV关于SOC的转移概率分布函数，构建AEVs动态负荷聚合模型，达到模型低维数与高精度的双重要求；在此基础上，设计AEVs辅助传统机组的调频控制模型，并提出基于稳定经济模型预测控制（Lyapunov-based Economic Model Predictive Control, LEMPC）的双模态AEVs联合调频控制策略，借助两种模态，在更大范围内兼顾系统频率控制稳定性与调控经济性。通过算例仿真表明，构建的聚合模型准确度高，基于LEMPC的联合调频策略在保证系统频率稳定的基础上进一步提高了调频过程中的经济性，由此验证了所提策略的有效性。

1 基于LEMPC的调频控制思路

1.1 充电过程的马尔科夫性描述

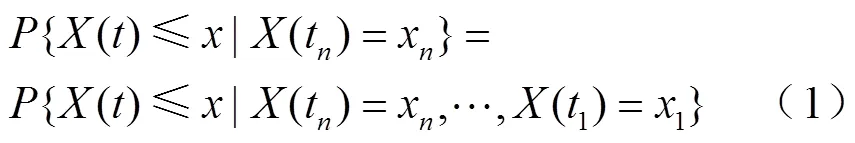
满足如上性质的随机过程称为马尔科夫过程，具有离散参数和离散状态空间的马尔科夫过程称为为马尔科夫链。马尔科夫链是一种描述随机转移过程的模型，从当前状态按一定的概率转移到下一状态，且未来状态仅与当前状态有关，而与历史状态无关。

EV充电是指电池从低电量状态向高电量状态转移的动态变化过程。一般采用SOC来表示电池的剩余电量，若将其记为状态，其离散时间下的递推公式可表示为

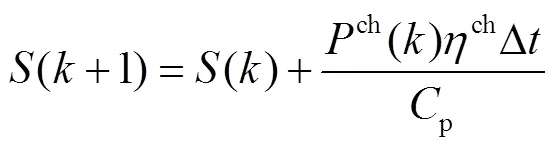
式中，(+1)和()分别为第+1时刻和第时刻的SOC；ch()为时刻的充电功率；ch为充电效率；P为电池的实际容量；∆为离散时间间隔。

根据式（2），电池SOC可看作一个离散的随机过程，且满足如下性质：(+1)的概率分布与EV的历史状态无关，仅取决于EV在时刻的状态，即符合马尔科夫链。因此，本文将EV的SOC离散化为数个状态空间，通过马尔科夫链表示各状态区间内负荷的动态转移过程。状态区间内的负荷在各区间之间的动态转移过程如图1所示，其中，S表示EV充电过程中某SOC区间；实线表示下个时刻状态区间S内负荷的动态转移路径；P,j表示从状态区间转为状态区间的转移概率，可用条件概率表示为

图1 EV负荷转移过程示意图

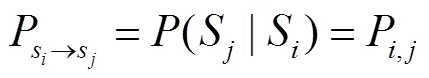
1.2 基于LEMPC的调频控制思路

为快速有效地抑制频率波动，本文提出了基于LEMPC的AEVs辅助传统机组联合调频控制策略，如图2所示。

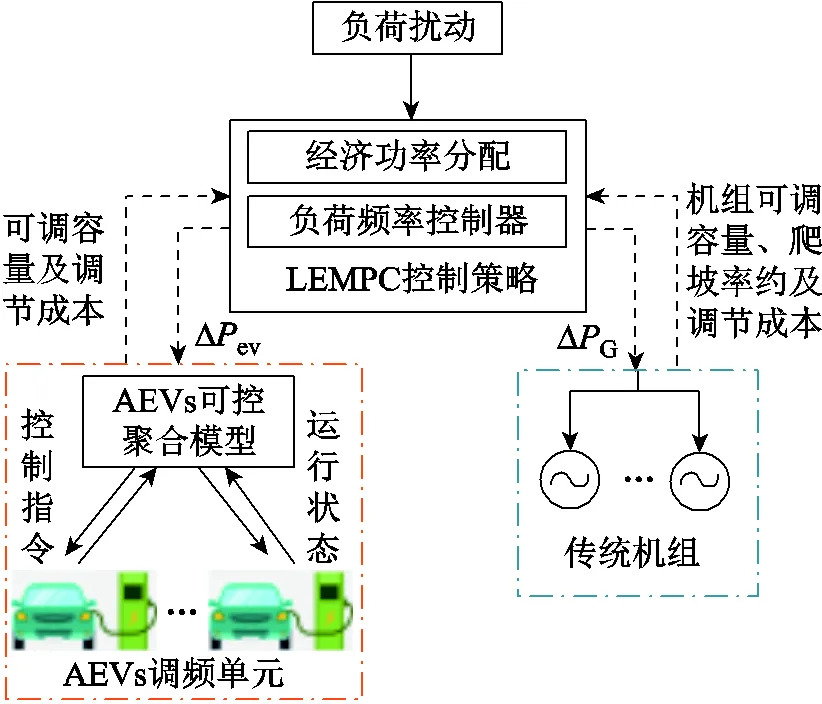
图2 基于LEMPC的设计思路

首先，将大规模可调度EV聚合建模形成一个便于电网调度的AEVs调频单元；接着，LEMPC控制策略根据EV调频单元以及各传统机组的出力约束和调节成本进行经济功率分配，确定各调频资源的稳态功率点；然后，负荷频率控制器通过双模态运行策略，在兼顾经济性与稳定性的前提下，实时调整各资源的功率指令，使各资源不断跟随稳定设定点；最后，各调频资源响应LEMPC控制器发出的功率指令，调整自身出力，完成调频。

LEMPC继承了EMPC优化过程经济性的优点，同时在控制过程中采用双模态运行策略，不仅考虑了系统的稳定性，还进一步扩大了优化自由度[17]，故可在保证系统频率稳定的前提下，进一步提升AEVs参与下负荷频率调节系统的经济性。

2 AEVs聚合模型及系统调频控制模型

2.1 AEVs充电过程聚合模型

2.1.1 充电过程转移概率计算方法

当前市面上EV品牌和电池厂商不计其数，不同的电池所对应的充电模式也不尽相同，主要包括慢速充电、常规充电和快速充电等模式，充电功率从几kW到几十kW不等。充电模式的不同，提升了AEVs聚合建模难度。因此，在EV参与聚合前根据充电模式进行分组，将充电功率、电池容量等特性参数相近的EV群体作为一个小聚合体进行建模，进而融合多个小群体的聚合模型得到整个大群体的拓展AEVs聚合模型。为此，在对EV进行聚合建模前，需要先确定可参与辅助调频的车辆。本研究对某时刻入网EV的信息进行收集，获取入网时刻、预计离网时刻、入网SOC、预计离网SOC、充电模式等参数，然后根据所收集的参数，对该时刻下EV是否具备辅助调频能力进行判断，符合条件的车辆将会被选取，不满足条件者进行强制充电直至离网。

具体而言，对于符合条件的车辆，首先根据EV电池容量进行一次分组，在此基础上根据充电功率进行二次分组，最后将二次分组后的车辆用于后续聚合模型的建立。从现场实施角度看，我国市场上各类型EV电池容量大都位于30～60kW·h之间，故依据电池容量的一次分组可将EV分为三类，即[30,40]kW·h、[40,50]kW·h和[50,60]kW·h。此外，EV主要有7kW慢速充电、15kW常规充电和40kW快速充电三种有代表性的充电模式，国标GB/T 20234.1—2015也要求EV充电设备进行统一配置以兼容不同品牌EV。为此，依据充电功率的二次分配可根据上述三种充电模式进一步实现电动汽车群体细分。由此，经过二次分组后的电动汽车具有相似的容量参数和相同的功率参数，建模时，对于某一群体的EV容量可取该类别的平均值作为标准量。

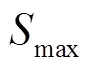
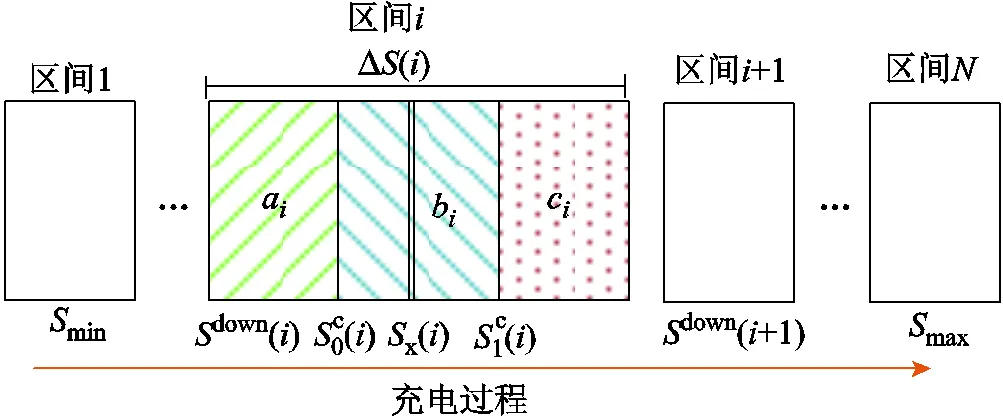
图3 相邻区间转移过程示意图

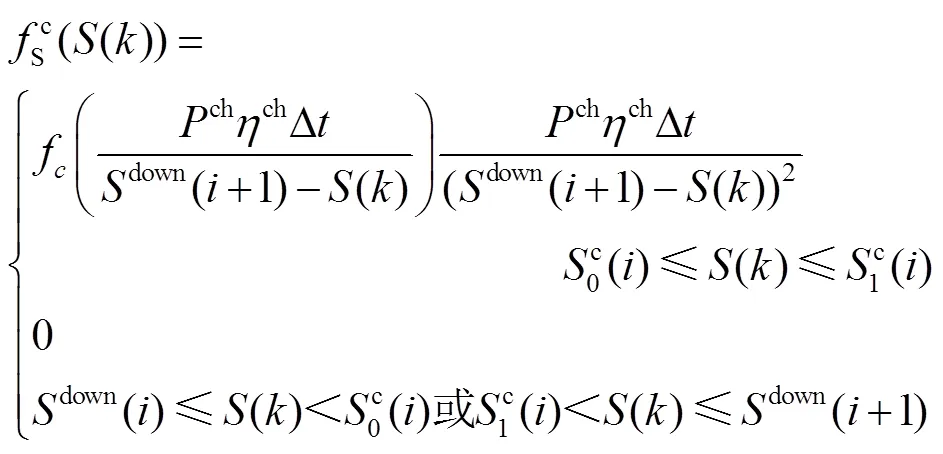
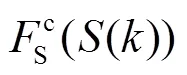
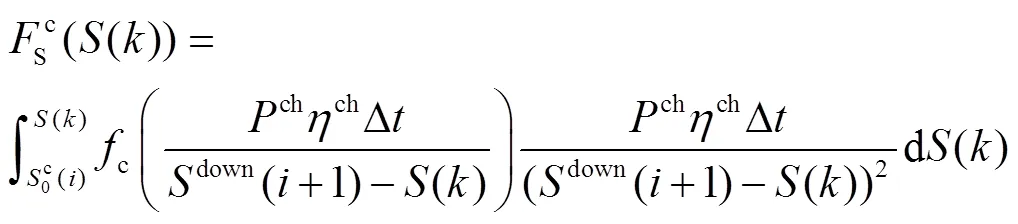
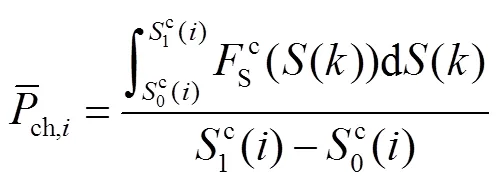
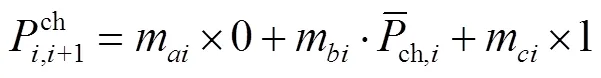
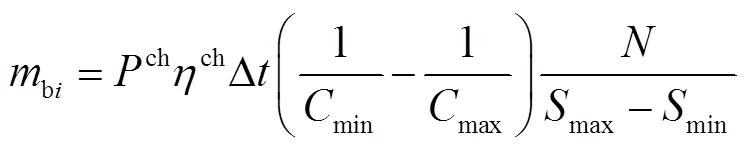
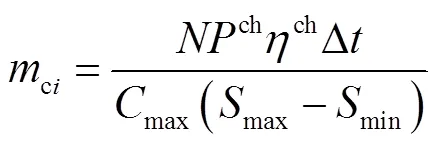
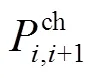
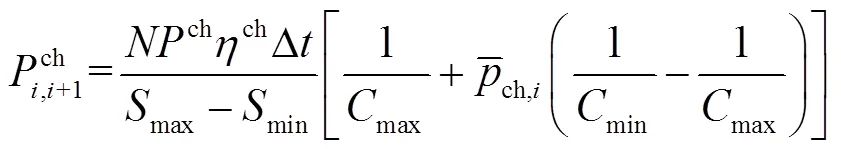
2.1.2 充电过程聚合模型

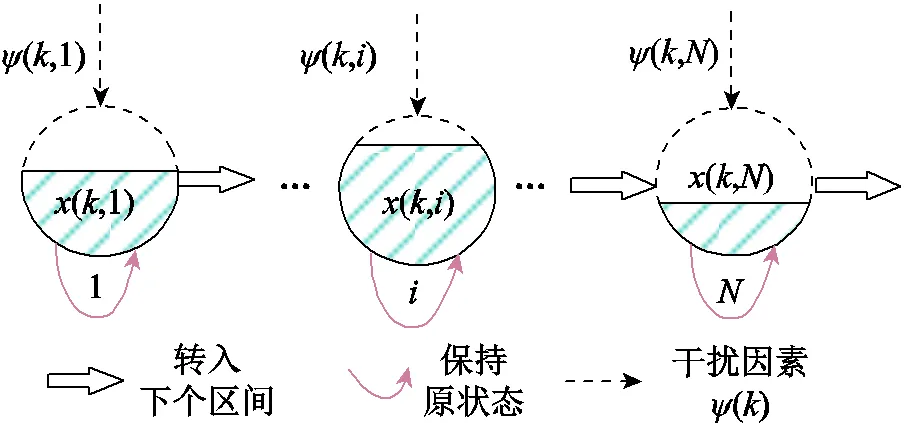
图4 充电负荷动态演化示意图

基于上述分析，充电负荷的动态转移过程可由状态空间方程（11）描述。

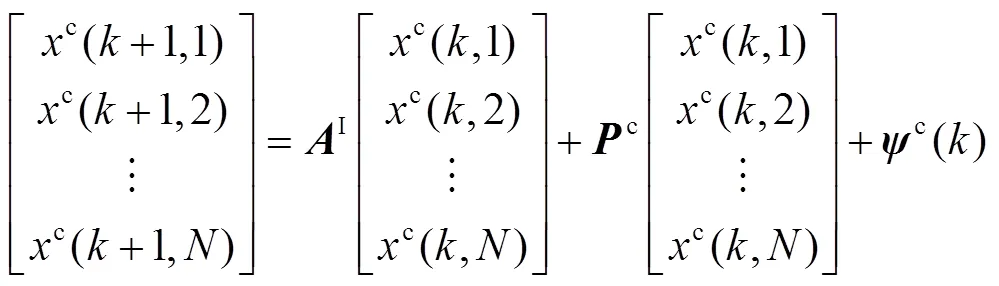
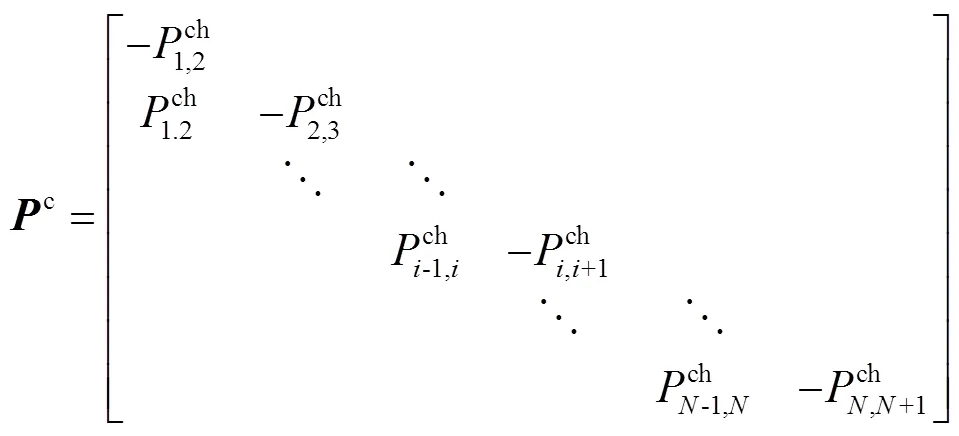
2.1.3 AEVs全状态可控聚合模型

AEVs闲置状态和放电状态下的聚合建模过程与上述充电过程类似，不再赘述，详见附录。

最终，基于上述三种状态下AEVs聚合模型，可整理出AEVs全状态聚合模型为

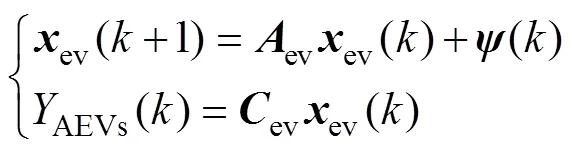
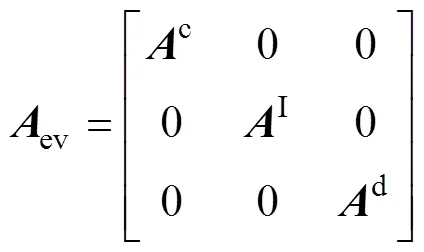
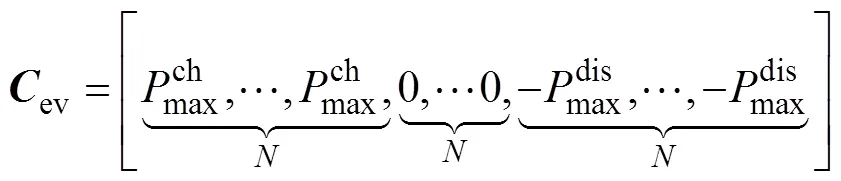
假设EV被分为个群体，将前文所述看作是第个群体的建模过程，则式（13）改写为

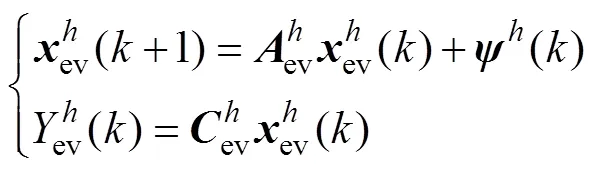
整合个群体模型，可得到EV整体拓展模型为

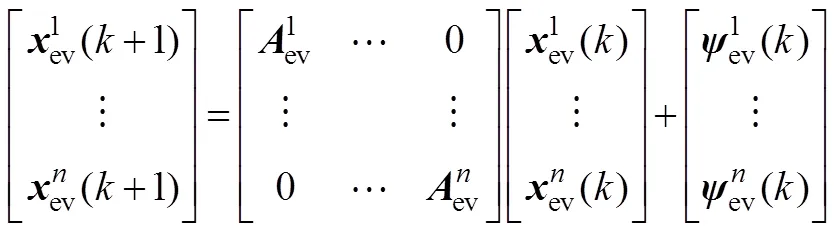
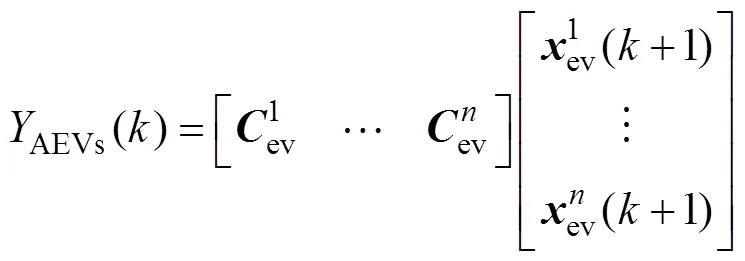
2.2 AEVs参与下的系统调频控制模型

2.2.1 两区域调频控制结构

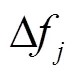
2.2.2 火电机组模型

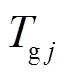
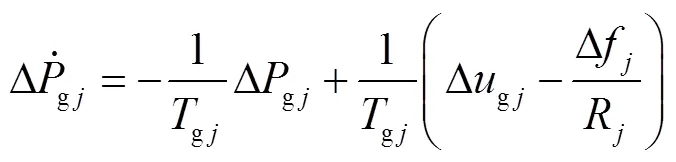
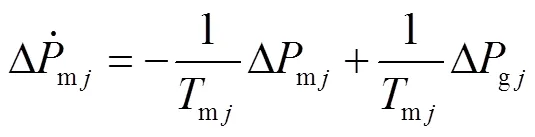
2.2.3 负荷频率模型

AEVs参与下各区域负荷频率偏差动态特性为

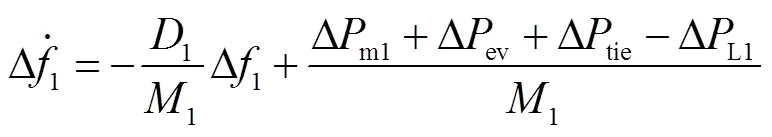
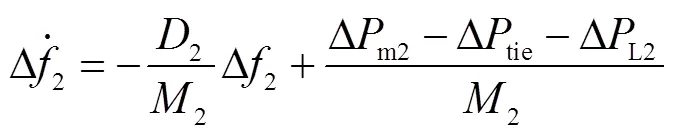
2.2.4 联络线功率及区域控制偏差模型

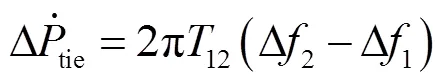
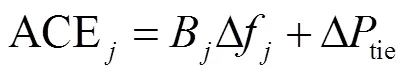
2.2.5 AEVs调频单元模型

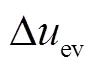
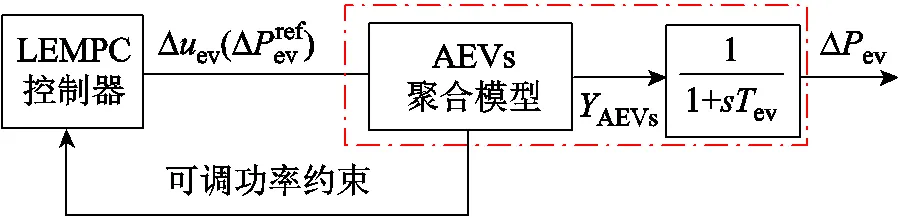
图5 AEVs调频单元结构

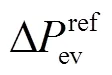
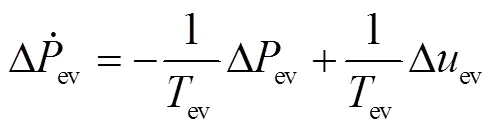
2.2.6 两区域调频控制模型

综上所述，AEVs参与下两区域调频控制模型可表示为

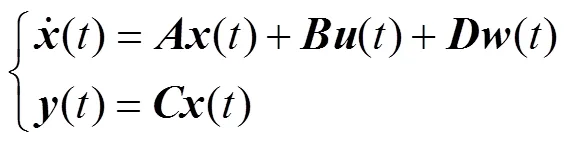
3 基于LEMPC的调频控制策略

3.1 经济功率分配—稳态经济最优点求解

为平衡区域电网中的负荷扰动，提高运行经济性，需进行功率经济分配，合理协调各调频资源的出力，其结果将作为LEMPC控制器的稳态最优设定值。本研究处理思路为：综合考虑各调频资源的约束条件，以最小化总调节成本为目标优化分配调频功率。

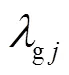
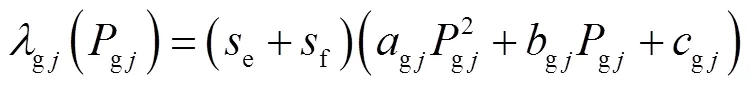
AEVs作为可调负荷，其调节成本主要来源于电池损耗[14]以及与电网互动的电价成本[20]，也将AEVs的调节成本描述为二次函数，即

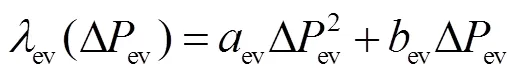
区域联络线功率调节成本则可直接表示为[16]

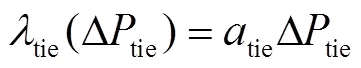
综上所述，稳态经济最优点求解模型可表示为

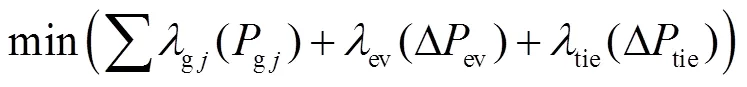
特殊地，考虑到EV的充电需求，当传统机组容量充足时，AEVs的功率稳态设定点应为0，即频率调节完成后，AEVs应恢复充电状态。

3.2 负荷频率控制—LEMPC控制器设置

LEMPC控制器应根据两区域内负荷扰动、频率偏差、ACE等信息统筹集中调节两区域调频资源出力，以实现频率的快速经济调节。基于LEMPC理论，设计了模型预测、综合性能指标优化、辅助控制器设计和双模态运行策略等四个实现步骤。

3.2.1 模型预测

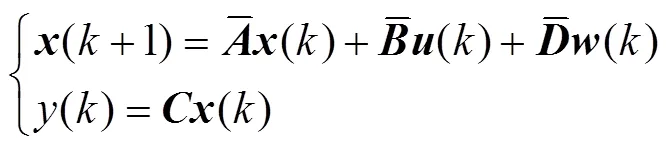
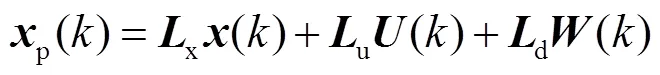
3.2.2 综合性能指标

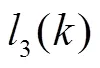
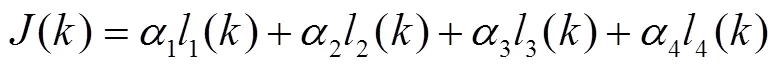
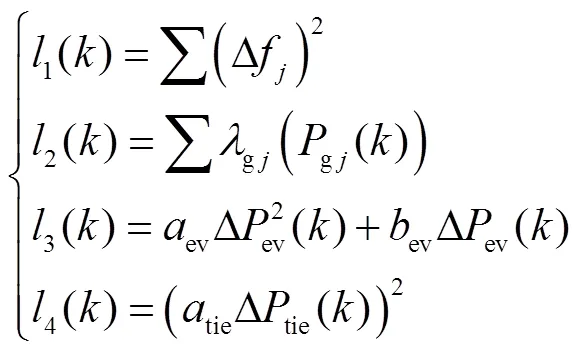
3.2.3 辅助控制器设置

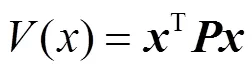
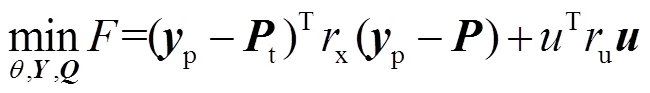
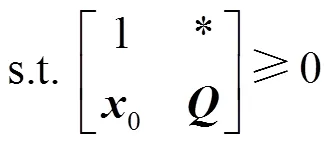
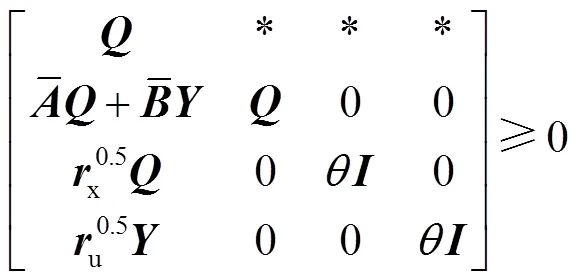
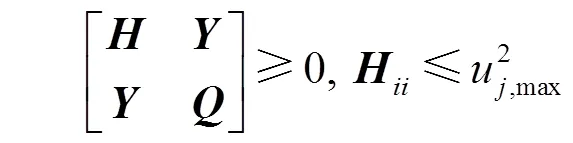
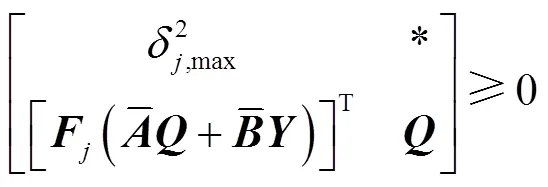
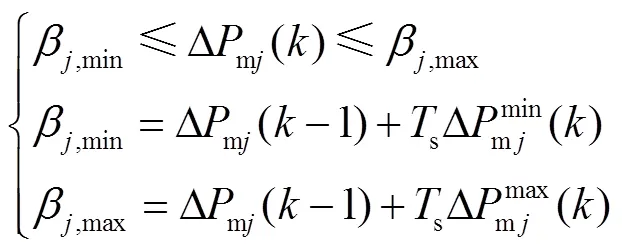
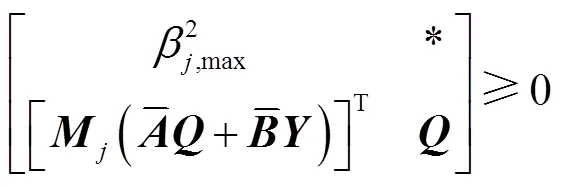
同理，可将联络线功率的幅值约束转换为

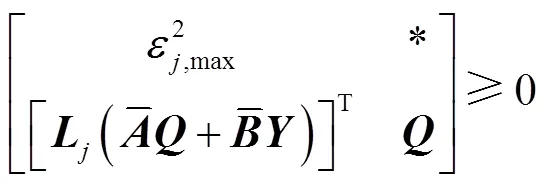
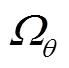
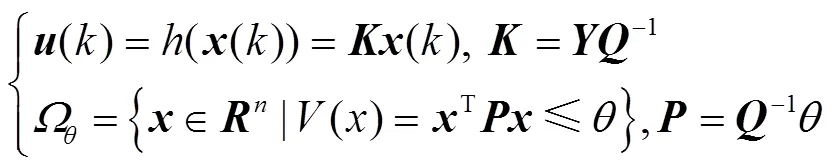
3.2.4 双模态运行策略

基于上述过程，时刻调频控制模型的LEMPC双模态运行优化问题可描述为

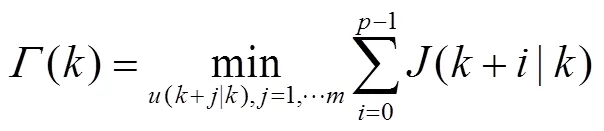
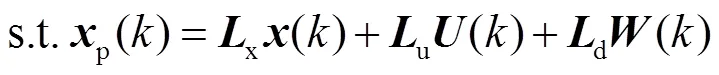
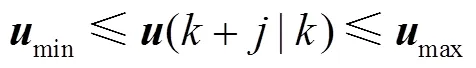
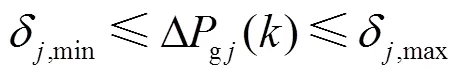
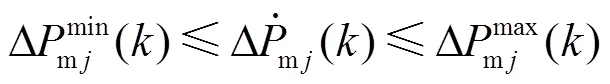
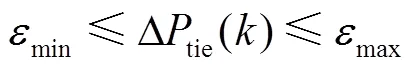
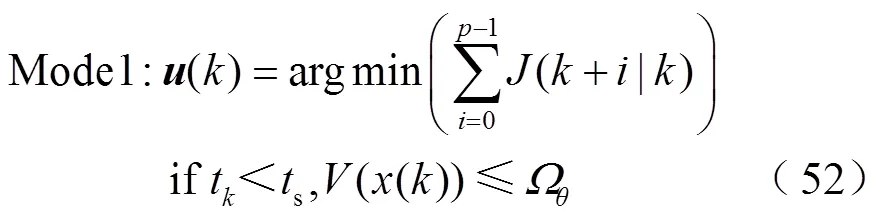
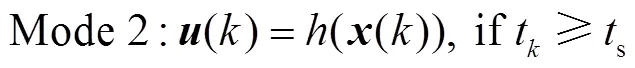
3.3 基于LEMPC的调频控制策略流程

由此，绘制LEMPC调频策略流程如图6所示。

图6 基于LEMPC的调频控制策略流程图

包括以下主要步骤：

（1）初始化系统运行状态，计算各区域调频资源可调功率范围。

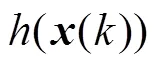
（5）控制器运行于模态1，以经济性指标为主，并在稳定域内优化目标函数式（46）。

4 仿真分析

4.1 基本参数

4.2 AEVs负荷聚合模型准确性

为验证所建AEVs聚合模型的准确性，选取由三种充电模式组成的电动车群体进行聚合仿真，并将它们的结果与AEVs直接聚合功率曲线进行对比。AEVs数量为2 500辆，一天24个时段的负荷流入量以及AEVs参数如图7所示。其中，AEVs的起始SOC为(0.45,0.15)；SOC上下限值分别为0.95和0.2；电池容量符合均匀分布；参与充电的起始荷电状态符合正态分布；SOC上下限、充/放电功率、充电效率等参数见表1。仿真步长选取4s，SOC区间数量选取20。

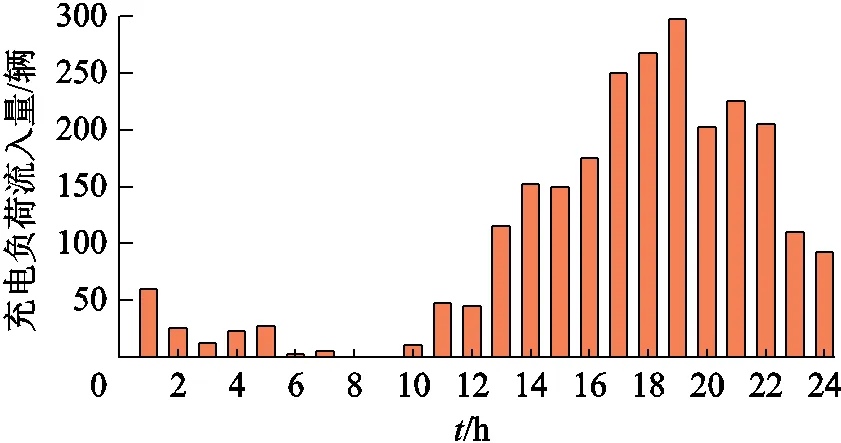
图7 某区域24h电动汽车流入量

表1 某区域AEVs仿真参数

Tab.1 Simulation parameters of AEVs in a certain area

图8给出了两种方法的对比仿真结果。可见，本文所建基于转移概率的AEVs聚合模型与直接功率模型聚合功率基本保持了一致，能够较准确地描述AEVs充电负荷的动态变化过程，同时，对于不同电池容量和充电功率的EV组，聚合模型输出功率与蒙特卡洛模拟法都保持了一致。而且，为达到同样的模型精度，与文献[22]方法相比，本文提出的转移概率求取方法大大降低了模型维数。

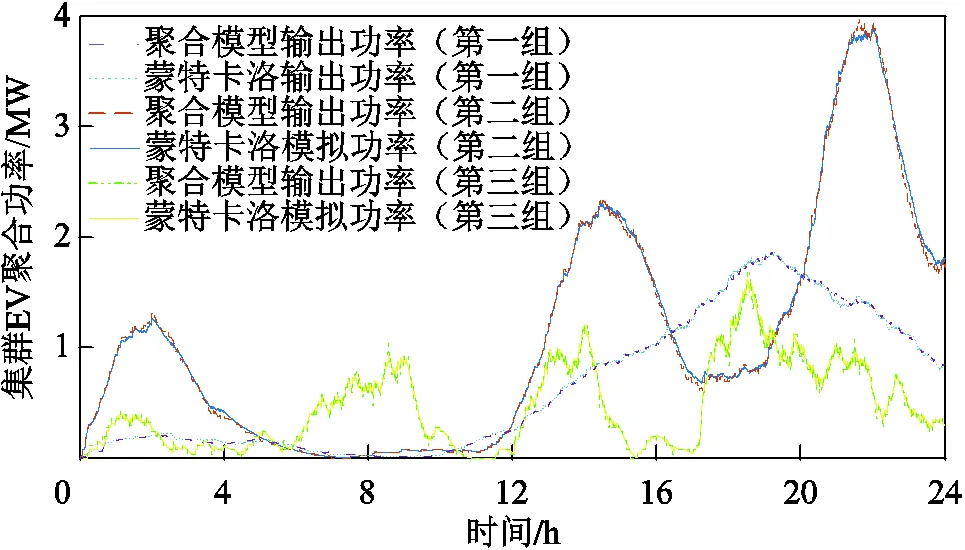
图8 聚合模型仿真功率曲线对比

进一步将三组EV统一进行蒙特卡洛模拟，与AEVs拓展聚合模型进行仿真对比。不同充电特性参数下基于拓展聚合模型的功率对比结果如图9所示。可见，通过分组聚合得到的AEVs拓展聚合模型能够准确描述不同充电特性EV负荷群体的动态演化过程。

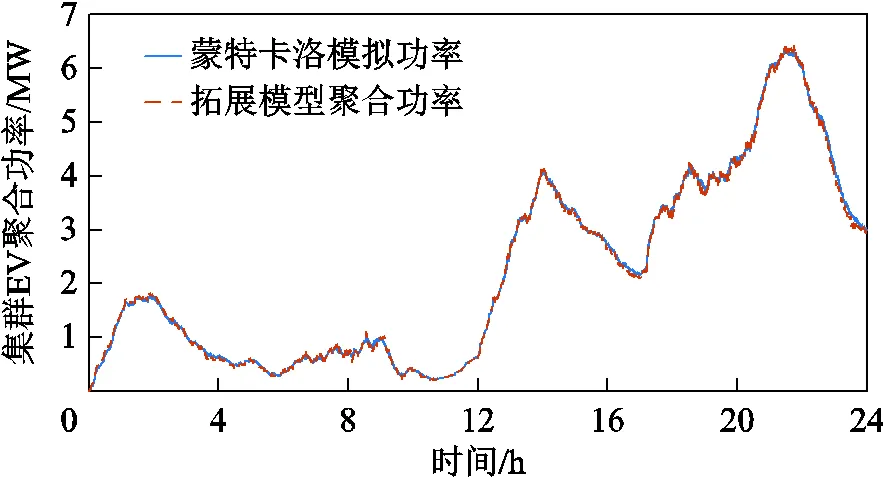
图9 拓展聚合模型输出功率仿真对比

4.3 控制效果

为更好地体现基于LEMPC调频控制策略的控制效果，同时更直观地反应调控细节，设置了三个扰动场景进行仿真分析。

EMPC中优化问题采用Matlab中Gurobi工具箱对控制问题进行求解。不同控制策略下系统动态响应曲线如图10所示。不同性能指标下两种控制策略的对比结果见表2。

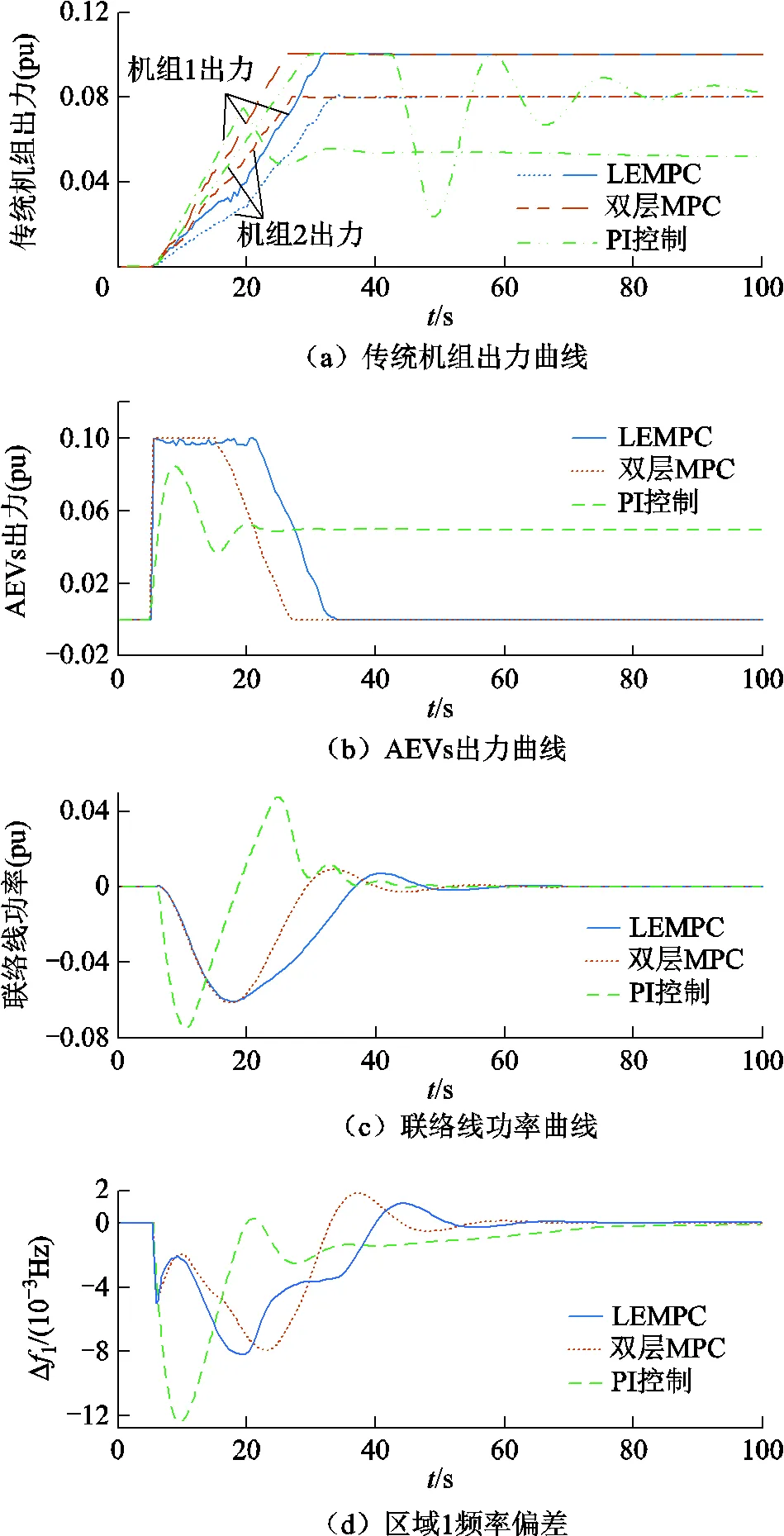
表2 控制策略对比结果（场景1）

Tab.2 Control scenario comparison results (scene1)

场景2是为了验证LEMPC在非零稳态最优设定点下的控制性能。此时，区域1可调容量不足，需联络线功率作支撑，经式（30）、式（31）优化给出稳态最优点。不同控制策略下系统动态响应过程如图11所示，不同控制策略对比结果见表3。可以看出，LEMPC仍可达到非零稳态最优设定点，且在动态性能相近的前提下，动态经济性优于双层MPC。

图11 不同控制策略下系统动态响应过程（场景2）

表3 控制策略对比结果（场景2）

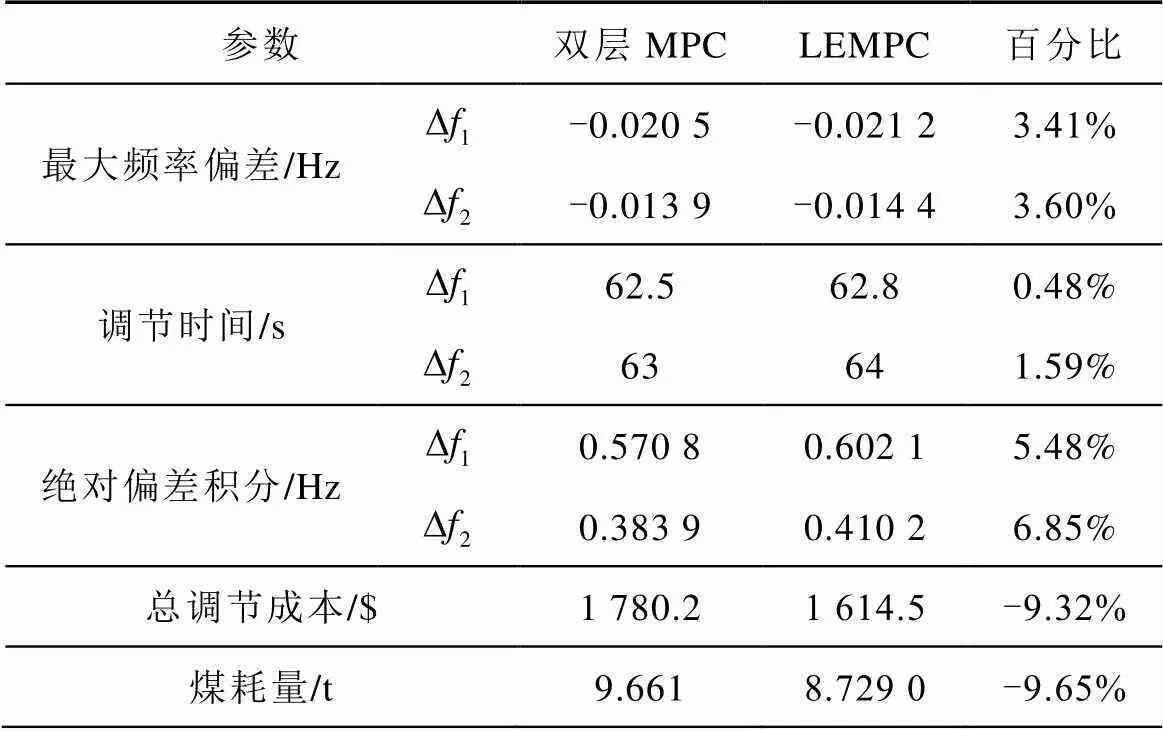
Tab.3 Control scenario comparison results (scene2)

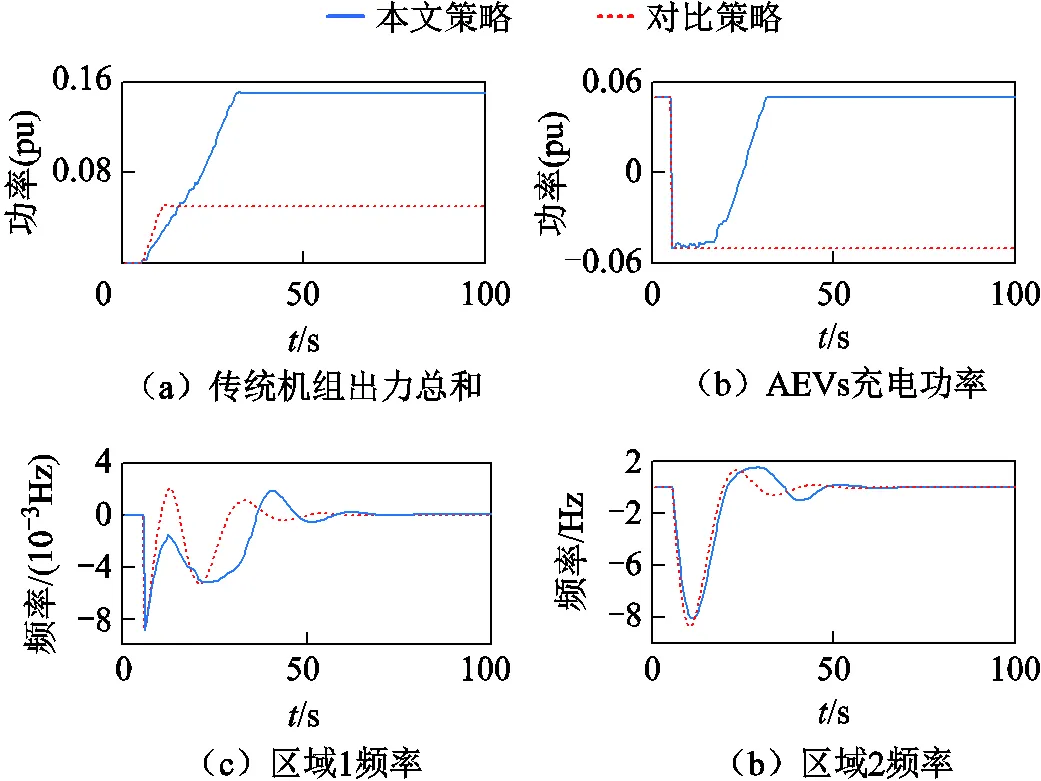
图12 不同策略下系统动态过程对比图（场景3）

图12表明，两种策略下系统频率偏差最大值相近，均有较好的动态性能，这是由于在扰动发生瞬间，两种策略下AEVs均以最大可调功率快速响应来提供功率支撑。但不同点在于，对比策略达到稳态时，最终由AEVs和传统机组共同承担功率缺额；而本文策略顾及到了AEVs的充电需求，让传统机组功率逐渐爬升并最终承担全部功率缺额，AEVs出力则随之减少，逐渐恢复充电状态，如图12a、图12b所示。因此，本文策略可以在保证调节性能的前提下，协调传统机组和AEVs的出力，相较于“EV集群优先”策略，增大了传统机组的出力，提升了AEVs的充电量，更好地满足了AEVs充电需求。

4.4 随机扰动下AEVs出力及对频率调节影响

4.4.1 AEVs出力仿真

为验证AEVs聚合模型对LEMPC优化EV出力的约束作用，选取18:00～20:00时段，对两区域互联系统分别施加随机扰动进行仿真分析。在随机负荷扰动下，AEVs的出力及其上、下限如图13所示。

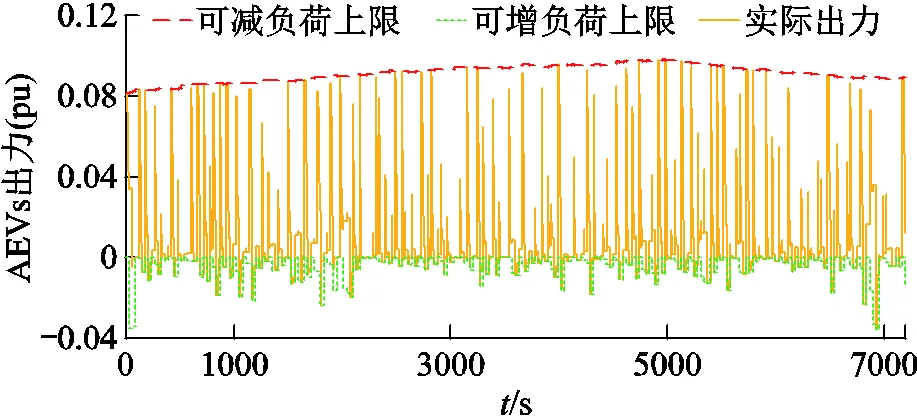
图13 AEVs实际出力及约束范围

由图13可见，AEVs的出力始终满足可调功率约束。进一步对比图9和图13可知，AEVs的可削减负荷上限始终是充电负荷的2倍，即全部充电的EV转变为放电状态时，AEVs可对外提供最大功率。反观可增负荷上限，明显小于可减负荷，且每个扰动产生瞬间数值参差不齐。这是由于LEMPC控制策略执行“传统机组为主、AEVs为辅”的调频理念，尽量保障EV的充电时长。当区域内传统机组容量充足时，AEVs的稳态设定点为0，即随着火电机组的功率爬升，AEVs出力逐渐恢复至初始状态（充电状态），从而使得扰动发生时AEVs最大可增加负荷取决于上个扰动调节结束时AEVs运行状态。

4.4.2 系统频率调节

为了进一步说明AEVs对系统频率调节的影响，以及本文所提策略的有效性，仍选取相同时段对两区域施加随机负荷扰动进行仿真，结果如图14和表4所示。

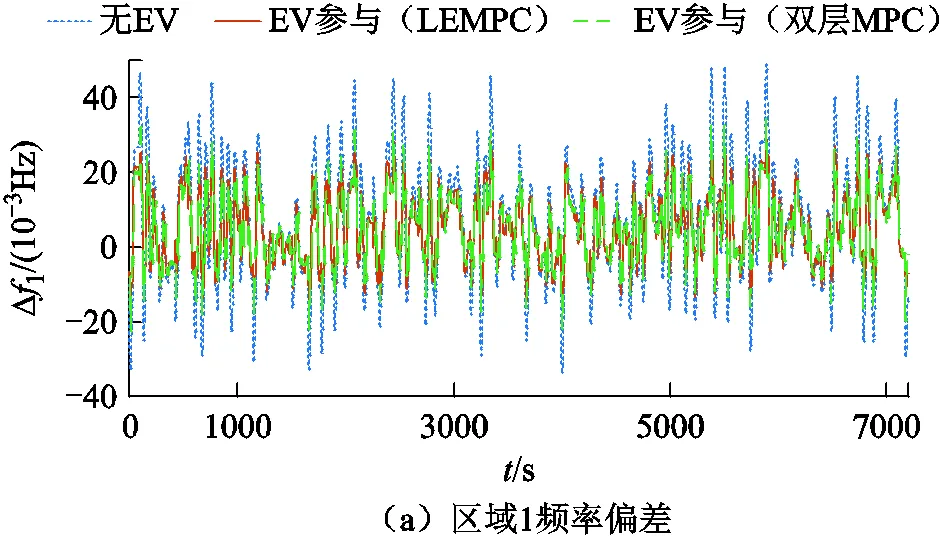
表4 有无EV参与频率调节对比结果

Tab.4 Comparison results of frequency regulation with and without EV

通过计算，并结合图14可知，AEVs参与调频能够更快速有效地抑制频率偏差。在两种不同的策略下，EV的参与均使区域频率调节性能改善，其中，在本文控制策略下两区域最大频率偏差分别降低了40.5%和38.9%，频率偏差方均根分别降低了34.4%和27.3%；双层MPC控制策略下两区域最大频率偏差分别降低了41.3%和40.9%，频率偏差方均根分别降低了35.6%和28.9%；调节性能相差甚微，但本文控制策略共节省调节成本$11 786。这表明在发生负荷扰动时AEVs能够快速响应，为系统提供功率支撑，同时，本文控制策略可以在满足频率调节要求的前提下进一步优化调节成本。

4.5 模型规模与求解速度

本文在模型聚合过程中选则SOC大区间数量=20，选取每个大区间下的小区间数量=10 000，在有效避免维数爆炸问题的同时也保证了在0.1s步长下SOC区间转移概率有足够的精度；小区间只参与一次一步转移概率的求解，故对聚合模型的求解速度基本不存在影响。将本文建立的AEVs聚合模型和控制策略在Intel Core i7-10875H CPU@ 2.30GHz和16GB的RAM计算平台上运行，并通过Matlab 2017b调用Gurobi工具箱对控制问题进行求解，每一次的控制量求解大约为0.005～0.01s。

5 结论

为弥补新能源电力系统中调频资源不足的问题，本文研究了AEVs参与电网调频的控制策略，得到以下结论：

1）利用马尔科夫链理论，提出了AEVs动态演化过程转移概率计算方法，构建了考虑电池容量差异的聚合模型，该模型能够准确地描述AEVs负荷动态演化过程，同时有效降低了聚合模型的维度。

2）基于两区域互联系统调频控制架构，提出了基于LEMPC的AEVs辅助电网双模态调频控制策略，模态1下追求稳定域内的综合性能指标，模态2通过线性反馈辅助控制器驱动系统快速收敛到稳态最优点。与双层MPC相比，该控制策略在保证系统频率稳定的前提下，进一步优化了频率调节过程的经济性。

3）提出的控制策略协调了各调频资源出力，充分利用了各类资源特性；通过发挥EV的快速响应特性，降低了区域频率偏差，提升了系统频率调节性能。

附 录

1. 闲置及放电状态聚合模型

闲置状态聚合模型为

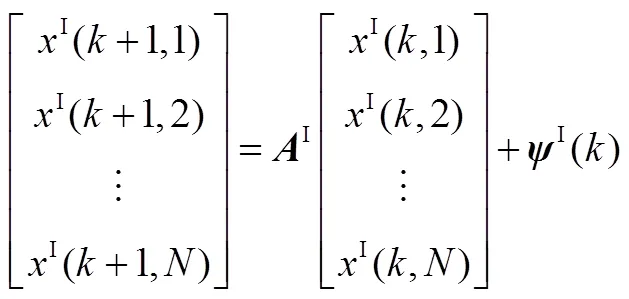
放电状态聚合模型为

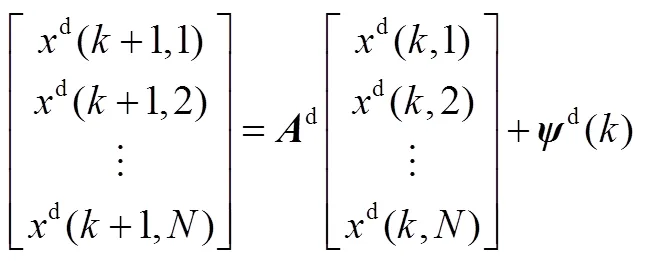
2. 典型两区域互联系统频率动态响应模型

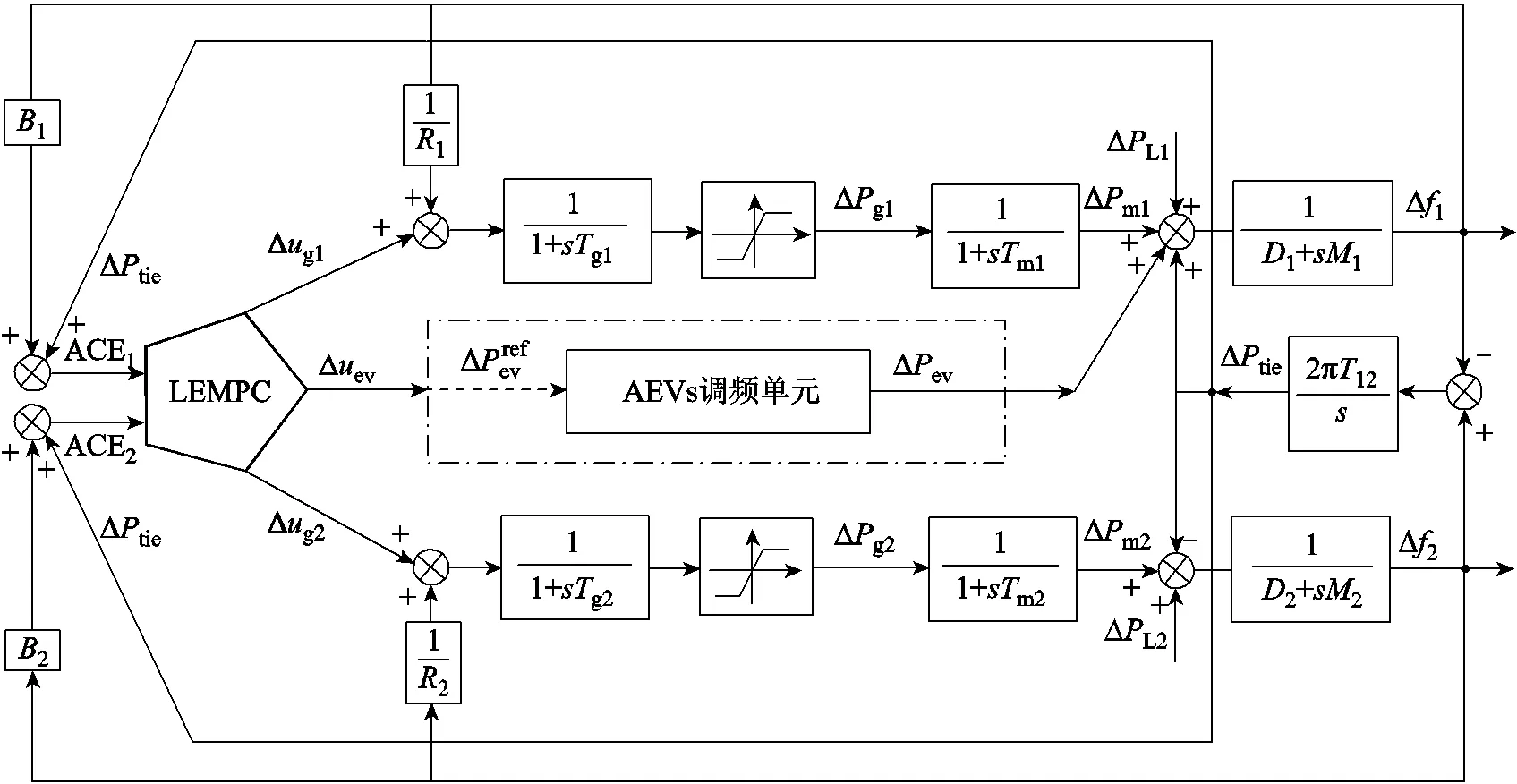
附图1 两区域电网频率动态响应模型

App.Fig.1 Frequency dynamic response model of two-area power grid

3. 两区域调频控制模型各参数矩阵元素

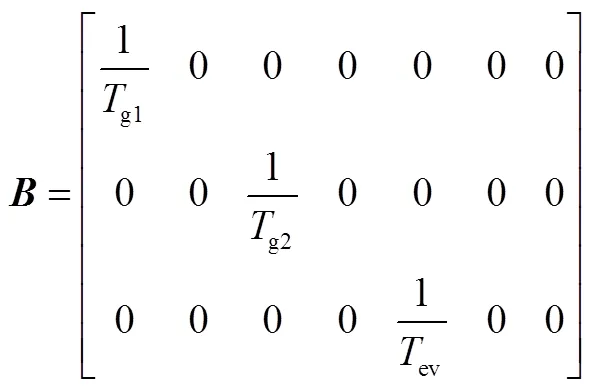
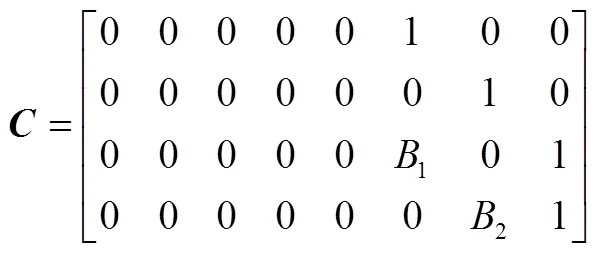
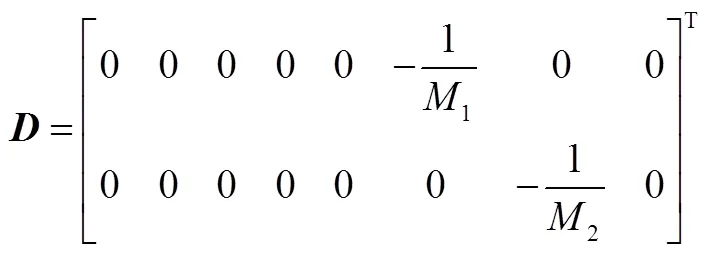
4. 调频资源模型参数

附表1 各调频资源模型参数

App.Tab.1 Frequency regulation resource model parameters

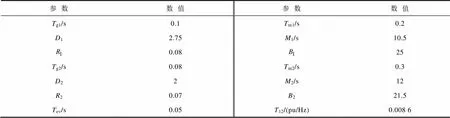
参数数值参数数值 Tg1/s0.1Tm1/s0.2 D12.75M1/s10.5 0.0825 Tg2/s0.08Tm2/s0.3 D22M2/s12 R20.07B221.5 Tev/s0.05T12/(pu/Hz)0.008 6

附表2 各调频资源经济性参数

App.Tab.2 Economic parameters of frequency regulation resources

参数数值参数数值 ag1/(t/pu2)1.7bg1/(t/pu)110 cg1/t5.16ag2/(t/pu2)3.2 bg2/(t/pu)140cg2/t6.52 se/($/pu)62.7sf/($/pu)30 aev/($/pu2)80bev/($/pu)100 atie/($/pu)220

5. 权重系数的选取

综合性能指标主要包含频率调节指标和经济性指标两部分。以AEVs和联络线功率调节成本为基准，选取权重系数为1；调节过程中应减少煤耗量以及气体排放量，火电机组调节成本权重系数选取略大于其他调节方式，选取系数为10；经济性指标确定后，改变频率调节指标权重系数进行仿真，分析系数对系统产生的影响，结果如附图2所示。

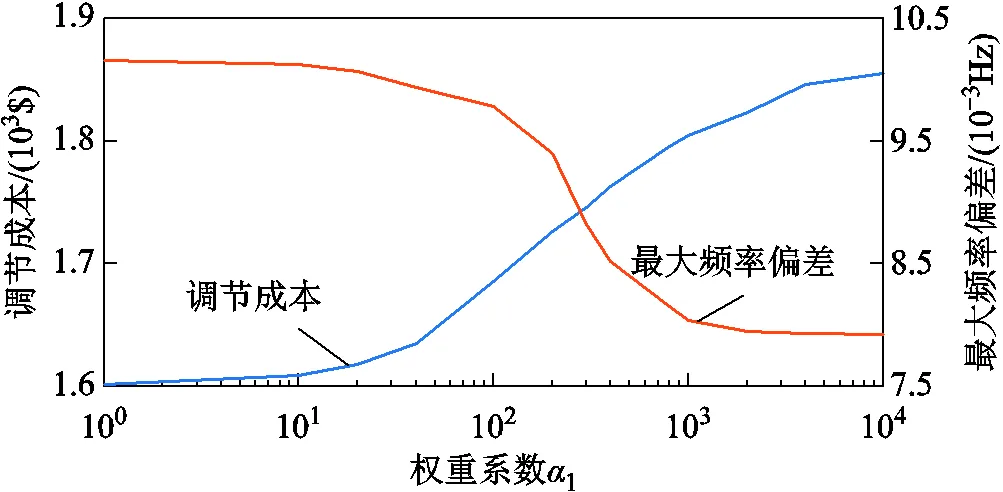
附图2 不同权重系数下优化结果

App.Fig.2 Optimization results under different weight coefficients

可见，当1取（100,102）时，成本与频率偏差变化速度缓慢，且此时频率偏差较大；当1取（102,103）时，调节成本随系数的增大而增大，同时，最大频率频率偏差急剧下降；当1取（103,104）时，最大频率偏差仍呈下降趋势，但变化幅度不大；而调节成本随着系数的增大仍保持增长趋势。基于上述分析，选取1=1000时，优化过程可以保证较好的频率调节性能，同时降低了调节成本。从以上过程可以看出不同权重系数的变化趋势，为了获取更加精确的权重系数，经过天牛须优化算法最终选取权重系数1、2、3和4分别为1 007.30、8.68、1.24和9.87。

[1] 姚一鸣, 赵溶生, 李春燕, 等. 面向电力系统灵活性的电动汽车控制策略[J]. 电工技术学报, 2022, 37(11): 2813-2824.

Yao Yiming, Zhao Rongsheng, Li Chunyan, et al. Control strategy of electric vehicles oriented to power system flexibility[J]. Transactions of China Electrotechnical Society, 2022, 37(11): 2813-2824.

[2] 张一媚, 董朝宇, 董晓红, 等. 含电动汽车集群调频的信息能源系统谱特征和稳定性评估[J]. 电力系统自动化, 2021, 45(2): 12-20.

Zhang Yimei, Dong Chaoyu, Dong Xiaohong, et al. Spectral feature and stability assessment for cyber-energy system with frequency regulation of electric vehicle cluster[J]. Automation of Electric Power Systems, 2021, 45(2): 12-20.

[3] 黄小庆, 陈颉, 谢啟波, 等. 用户充电选择对电网充电调度的影响[J]. 电工技术学报, 2018, 33(13): 3002-3011.

Huang Xiaoqing, Chen Jie, Xie Qibo, et al. The influence of users' charging selection on charging schedule of power grid[J]. Transactions of China Electrotechnical Society, 2018, 33(13): 3002-3011.

[4] 吴赋章, 杨军, 林洋佳, 等. 考虑用户有限理性的电动汽车时空行为特性[J]. 电工技术学报, 2020, 35(7): 1563-1574.

Wu Fuzhang, Yang Jun, Lin Yangjia, et al. Research on spatiotemporal behavior of electric vehicles considering the users' bounded rationality[J]. Transactions of China Electrotechnical Society, 2020, 35(7): 1563-1574.

[5] 吴洲洋, 艾欣, 胡俊杰. 需求侧灵活性资源参与调频辅助服务的备用优化与实时调度[J]. 电力系统自动化, 2021, 45(6): 148-157.

Wu Zhouyang, Ai Xin, Hu Junjie. Reserve optimization and real-time scheduling of frequency regulation ancillary service with participation of flexible resource on demand side[J]. Automation of Electric Power Systems, 2021, 45(6): 148-157.

[6] Bashash S, Fathy H K. Modeling and control of aggregate air conditioning loads for robust renewable power management[J]. IEEE Transactions on Control Systems Technology, 2013, 21(4): 1318-1327.

[7] 艾欣, 赵阅群, 周树鹏. 适应清洁能源消纳的配电网集群电动汽车充电负荷模型与仿真研究[J]. 中国电力, 2016, 49(6): 170-175.

Ai Xin, Zhao Yuequn, Zhou Shupeng. Study on aggregate electric vehicle charging load model and simulation for clean energy accommodation in distribution network[J]. Electric Power, 2016, 49(6): 170-175.

[8] Le Floch C, Kara E C, Moura S. PDE modeling and control of electric vehicle fleets for ancillary services: a discrete charging case[J]. IEEE Transactions on Smart Grid, 2018, 9(2): 573-581.

[9] 陆婷婷. 空调负荷的储能建模和控制策略研究[D]. 南京: 东南大学, 2015.

[10] 张谦, 周林, 周雒维, 等. 计及电动汽车充放电静态频率特性的负荷频率控制[J]. 电力系统自动化, 2014, 38(16): 74-80.

Zhang Qian, Zhou Lin, Zhou Luowei, et al. Load frequency control considering charging and discharging static frequency characteristics of electric vehicles[J]. Automation of Electric Power Systems, 2014, 38(16): 74-80.

[11] 鲍谚, 贾利民, 姜久春, 等. 电动汽车移动储能辅助频率控制策略的研究[J]. 电工技术学报, 2015, 30(11): 115-126.

Bao Yan, Jia Limin, Jiang Jiuchun, et al. Research on the control strategy of electric vehicle mobile energy storage in ancillary frequency regulation[J]. Transactions of China Electrotechnical Society, 2015, 30(11): 115-126.

[12] 季振亚. 能源互联网包容下电动汽车储能及气电互联的市场化设计[D]. 南京: 东南大学, 2018.

[13] 虞临波, 寇鹏, 冯玉涛, 等. 风储联合发电系统参与频率响应的模型预测控制策略[J]. 电力系统自动化, 2019, 43(12): 36-43.

Yu Linbo, Kou Peng, Feng Yutao, et al. Model predictive control strategy for combined wind-storage system to participate in frequency response[J]. Automation of Electric Power Systems, 2019, 43(12): 36-43.

[14] 樊国东, 刘世林, 裴俊, 等. 光火储混合发电系统的负荷频率协调优化控制[J]. 电力系统及其自动化学报, 2020, 32(12): 134-143.

Fan Guodong, Liu Shilin, Pei Jun, et al. Load frequency coordinated optimization control of hybrid power generation system consisting of PV, thermal power and energy storage[J]. Proceedings of the CSU-EPSA, 2020, 32(12): 134-143.

[15] 张舒鹏, 董树锋, 徐成司, 等. 大规模储能参与电网调频的双层控制策略[J]. 电力系统自动化, 2020, 44(19): 55-62.

Zhang Shupeng, Dong Shufeng, Xu Chengsi, et al. Bi-level control strategy for power grid frequency regulation with participation of large-scale energy storage[J]. Automation of Electric Power Systems, 2020, 44(19): 55-62.

[16] 廖小兵, 刘开培, 乐健, 等. 基于双层模型预测结构的跨区域AGC机组协同控制策略[J]. 中国电机工程学报, 2019, 39(16): 4674-4685, 4970.

Liao Xiaobing, Liu Kaipei, Le Jian, et al. Coordinated control strategy for AGC units across areas based on Bi-level model predictive control[J]. Proceedings of the CSEE, 2019, 39(16): 4674-4685, 4970.

[17] Heidarinejad M, Liu J, Christofides P D. Economic model predictive control of nonlinear process syetems using Lyapunov techniques[M]. London: Advances in Industrial Control, 2017.

[18] 董锴, 蔡新雷, 崔艳林, 等. 基于马尔科夫链的电动汽车聚合建模及多模式调频控制策略[J]. 电网技术, 2022, 46(2): 622-631.

Dong Kai, Cai Xinlei, Cui Yanlin, et al. Aggregation modeling based on Markov chain and multi-mode control strategies of aggregated electric vehicles for frequency regulation[J]. Power System Technology, 2022, 46(2): 622-631.

[19] 黄际元, 李欣然, 曹一家, 等. 面向电网调频应用的电池储能电源仿真模型[J]. 电力系统自动化, 2015, 39(18): 20-24, 74.

Huang Jiyuan, Li Xinran, Cao Yijia, et al. Battery energy storage power supply simulation model for power grid frequency regulation[J]. Automation of Electric Power Systems, 2015, 39(18): 20-24, 74.

[20] 李清, 张孝顺, 余涛, 等. 电动汽车充换电站参与电网AGC功率分配的成本一致性算法[J]. 电力自动化设备, 2018, 38(3): 80-87, 95.

Li Qing, Zhang Xiaoshun, Yu Tao, et al. Cost consensus algorithm of electric vehicle charging station participating in AGC power allocation of grid[J]. Electric Power Automation Equipment, 2018, 38(3): 80-87, 95.

[21] Kothare M V, Balakrishnan V, Morai M. Robust constrained model predictive control using linear matrix inequalities[J]. Automatica, 1996, 32(10): 1361-1379.

[22] Koch S, Mathieu J, Callaway D. Modeling and control of aggregated heterogeneous thermostatically controlled loads for ancillary services[C]//Power System Computation Conference, Stockholm, Sweden, 2011: 22-26.

[23] Khan A T, Cao Xinwei, Li Shuai, et al. Quantum beetle antennae search: a novel technique for the constrained portfolio optimization problem[J]. Science China Information Sciences, 2021, 64(5): 1-14.

Auxiliary Frequency Regulation Control Strategy of Aggregated Electric Vehicles Based on Lyapunov-Based Economic Model Predictive Control

Yu Yang1,2Zhang Ruifeng1,2Lu Wentao1,2Mi Zengqiang1,2Cai Xinlei3

（1. State Key Laboratory of Alternate Electrical Power System With Renewable Energy Sources North China Electric Power University Baoding 071003 China 2. Key Laboratory of Distributed Energy Storage and Microgrid of Hebei Province North China Electric Power University Baoding 071003 China 3. Electric Power Dispatching Control Center of Guangdong Grid Co. Ltd Guangzhou 510600 China）

Aiming at the problems of ignoring the differences among individuals for electric vehicles (EV) aggregation modeling and difficulty in balancing economy and stability simultaneously for frequency regulation assisted with EV, firstly, a transition probability calculation method considering the difference of battery capacity for the dynamic change process of EV was proposed based on Markov theory and the transition probability distribution function of the state of charge is derived. An aggregation model of EV was established and a combined frequency regulation model of typical two-area interconnection system participated by EV was built. Then, the dual-mode frequency regulation scenario based on the Lyapunov-based economic model predictive control was proposed. The adjustment cost through economic model prediction was reduced by Mode 1, and the system stability is guaranteed by Mode 2 using the auxiliary controller. Finally, the simulation results show that the aggregation model has high precision, and the control strategy can optimize the economy in regulation process while maintaining frequency stability.

Electrics vehicle，transition probability，aggregation model，load frequency control，Lyapunov-based economic model predictive control

10.19595/j.cnki.1000-6753.tces.220538

TM73;U491.8

国家重点研发计划资助项目（2018YFE0122200）。

2022-04-07

2022-06-10

余 洋 男，1982年生，博士，副教授，博士生导师，研究方向为电力储能技术、柔性负荷建模与调度等。E-mail：ncepu_yy@163.com（通信作者）

张瑞丰 男，1999年生，硕士研究生，研究方向为主动配电网、车网互动等。E-mail：1196515347@qq.com

（编辑 赫蕾）