青霉素发酵过程软测量建模仿真研究

崔浩阳，李凌

(沈阳化工大学 信息工程学院，辽宁 沈阳 110142)

针对传统测量方法存在诸如操作复杂、价格昂贵、滞后时间长、测量误差大等缺点[1]，软测量思想应运而生，通过选取与测量变量相关性大的辅助变量，并建立主变量与辅助变量之间关系，间接估算主变量的技术称之为软测量[2]。目前，软测量技术广泛应用到各行各业中，包括炼油、造纸、医药等，具体可应用在实时估计、质量估计和智能校正等方面[3]。

在工业过程中，数据量大且变量维数高，变量之间存在很大的相关性，因此，在建模之前，提取数据特征并且对数据进行降维是非常重要的。目前对软测量建模数据降维的研究越来越多，刘聪等人利用稀疏自编码器提取数据的特征，并用互信息对数据降维[4]；赵荣荣等人利用k-近邻互信息改进互信息，提取出与输出变量相关性更大的变量[5]；Jie等人结合热轧过程机理和变量间的互信息对输入变量降维[6]；孙丽娜等人利用平均影响值方法找到对输出变量影响较大的输入变量[7]；Wu等人利用套索算法对输入变量降维[8]。

自动编码器是一种无监督的机器学习算法，它对于提取数据特征是非常有效的。在自动编码器的隐含层的节点加入一个稀疏限制被称为稀疏自编码器。加入稀疏限制使提取出的数据特征更有意义,但是稀疏自编码器把所有变量看做同等地位，会引入冗余变量，使建模的过程更加复杂，因此需要剔除冗余变量。k-近邻互信息是用来计算两个对象之间的相关性,通过计算出变量之间的相关性，剔除相关性较小的变量。

本文针对青霉素发酵过程，利用k-近邻互信息剔除冗余变量，利用稀疏自编码器提取数据的特征，避免出现过拟合现象，结合最小二乘支持向量机进行软测量建模。经仿真验证，利用k-近邻互信息选择辅助变量的预测效果优于仅利用互信息选择辅助变量的预测效果，且降维至只有4个辅助变量时，预测效果同样良好。

1 相关理论

1.1 软测量模型

软测量技术与传统的测量方法有很大不同，软测量对生物量的测量是利用软件代替传统的仪表。在实际测量过程中，很多重要的变量，也就是主导变量都是难以测量的，而软测量技术就是选择可测变量，即辅助变量，利用它和主导变量之间的关系建立软测量模型，用软件来代替硬件(传感器)功能[9]。软测量模型如图1所示。

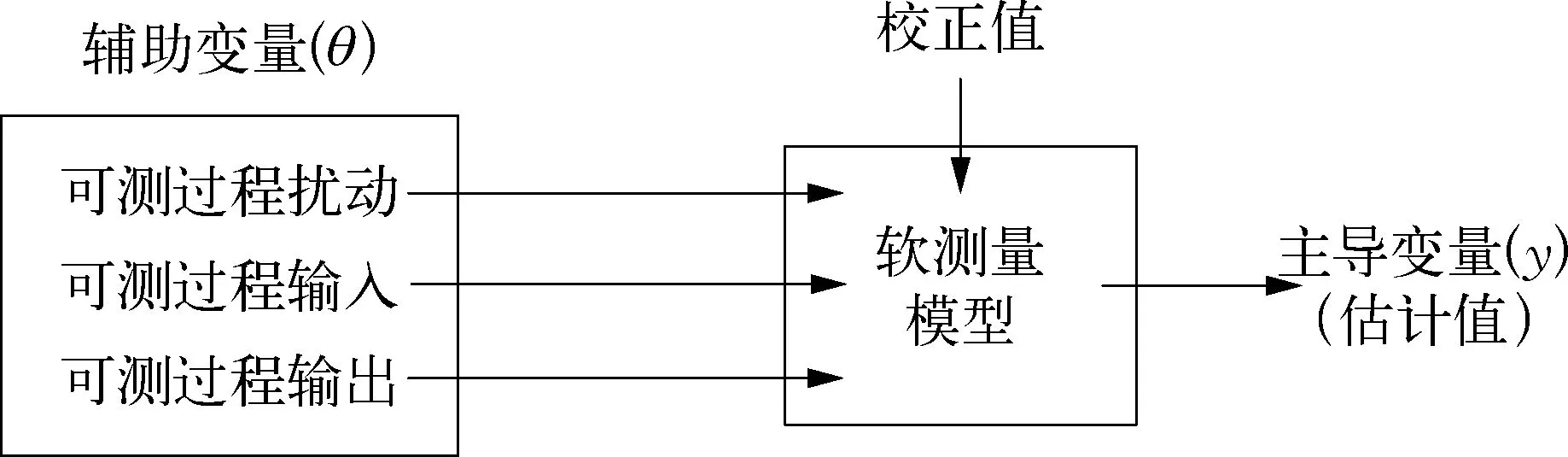
图1 软测量模型示意

构造辅助变量θ到主导变量y的函数是构造软测量模型的本质，可表示为

y=f(θ)

(1)

其中，辅助变量包括可测过程扰动、可测过程输入和可测过程输出。

1.2 稀疏自编码器

自动编码器是一种包括输入层、隐含层和解码层的3层神经网络。重构其输入，使其隐藏层学习到该输入的良好表征是该网络的目标，其结构如图2所示。

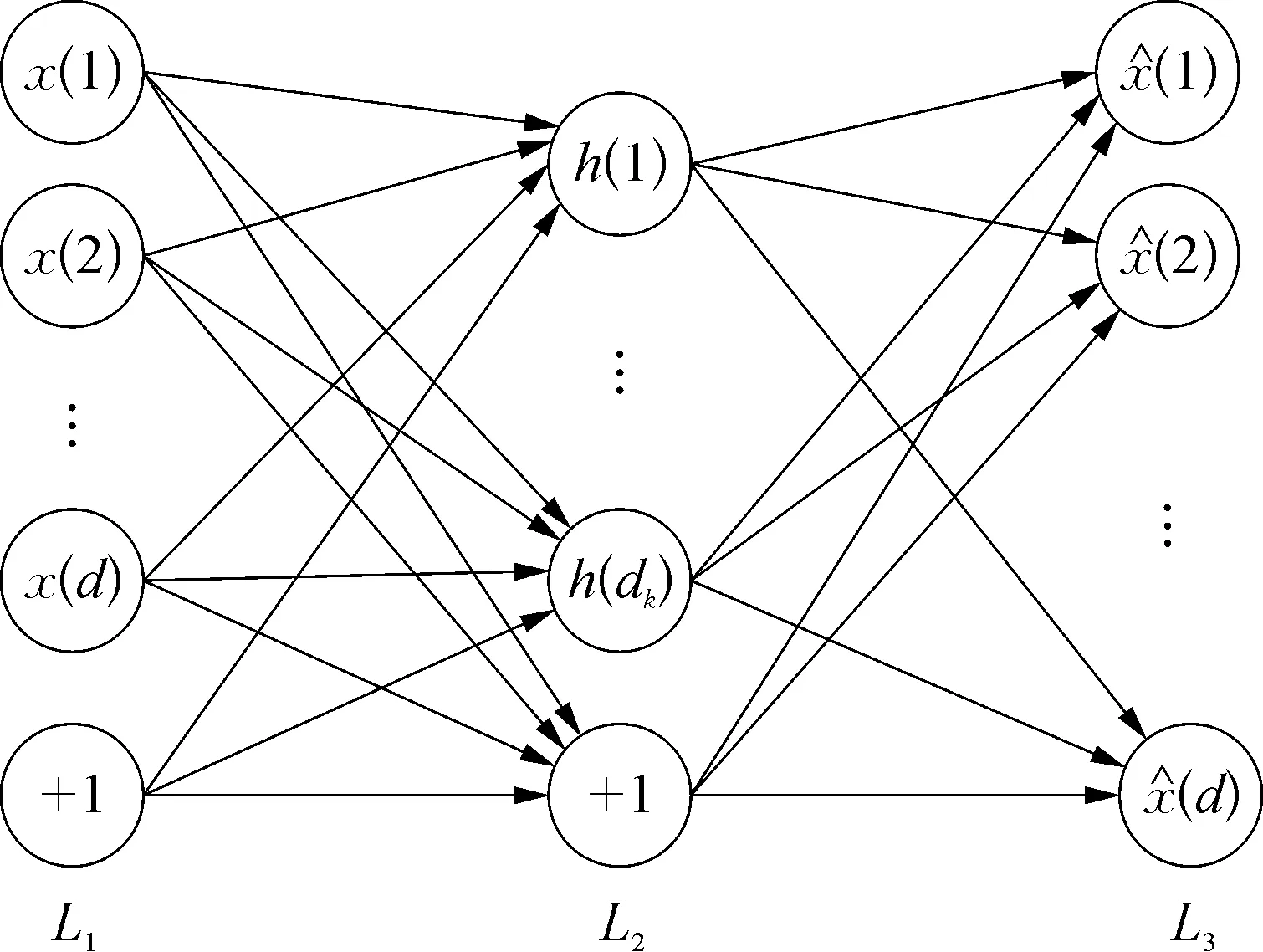
图2 自动编码器结构示意

图2中，输入层为L1层，隐含层为L2层，输出层为L3层。自动编码器的实质就是学习一个函数使得：

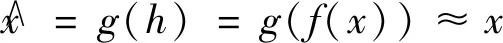
(2)

简单来说，自动编码器就是让输出等于输入。

为提取出更有意义的数据特征，且避免出现过拟合现象，采用稀疏自编码器。在自动编码器隐含层加入1个稀疏限制就是稀疏自编码器，它有激活和抑制两种状态： 激活状态是神经元的输出接近于1的时候，抑制状态是输出接近于0的时候，稀疏性限制是神经元在大部分时间都处于抑制状态[10]。

稀疏自编码器的平均激活度函数可表示为

(3)

其中，隐含层的第j个神经元对第i个样本的激活值用h(j,xi)表示。为了使平均激活度接近于零，即达到稀疏性，在函数中加入1个惩罚因子，可以使用相对熵，如式(4)所示：

(4)

1.3 k-近邻互信息

对于稀疏自编码器来说，样本每一维度的数据的地位都是相等的，但是每个输入变量与输出变量的相关性是不同的。因此需要对样本数据降维，剔除冗余变量，这样更能保证提取出来的特征是和输出相关的，提高建模精度。互信息是一种非线性、无模型、无数据的机器学习算法，它能够很好地衡量2个变量之间的相关性。

2个随机变量X和Y之间的互信息可表示为式(5)所示：

(5)

式中：p(X,Y)——X和Y之间的联合概率密度；p(X)，p(Y)——X，Y的边缘概率密度。

求解变量之间的概率密度是利用互信息计算相关性中最重要的部分，但是在实际软测量过程中概率密度是未知的。但是变量之间的相关性可以直接利用k-近邻互信息估计，并且该方法不需要计算概率密度。首先找出在随机变量X和Y构成的空间中给定的n个样本的k近邻，再找出其他样本分别在X和Y方向到当前样本的距离小于当前样本到k个近邻距离的最大值的数目，通过统计数目估计变量之间的互信息称为k-近邻互信息[11]。最后根据计算出的互信息选择与输出变量相关性较大的变量，并修正稀疏自编码器的重构误差。

2 最小二乘支持向量机软测量建模

作为一种非常有效的机器学习方法，支持向量机模式识别和函数逼近等领域得到非常广泛的应用，同时支持向量机对于解决非线性、小样本和高维度等问题效果良好[12]。将输入向量映射到高维特征空间，在高维特征空间中构造最优决策函数是支持向量机的基本思路[13]。假设训练样本为(xi,yi),i=1, 2, …,n，利用非线性映射φ(·)将样本的输入空间R4映射到特征空间如式(6)所示：

ψ(x)=(φ(x1),φ(x2), …,φ(xn))

(6)

在特征空间中构建最优决策函数如式(7)所示：

y=wTφ(x)+b

(7)

式(7)中，模型参数w和b可利用结构风险最小化准则求得，其中结构风险R的计算如式(8)所示：

(8)

式中：c——正规化参数；Remp——损失函数。不同于支持向量机，最小二乘支持向量机的损失函数为二次损失函数[14]，如式(9)所示：

(9)

式中：ξi——预测误差。根据结构最小化准则，最小二乘支持向量机的目标函数如式(10)所示：

s.t.yi=wTφ(xi)+bi=1, 2, …,n

(10)

利用拉格朗日法求解正规化参数c如式(11)所示：

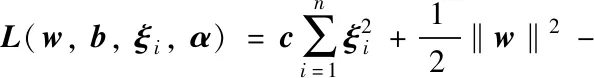
(11)

式中：α——拉格朗日乘子。

根据优化条件：

(12)

可得：

(13)

(14)

2cξi=αi

(15)

yi=wTφ(xi)+b+ξi

(16)

消除w和ξi，可得线性方程组如式(17)所示：

(17)

其中，

A=[1, 1, …, 1]T

(18)

α=[α1,α2, …,αn]T

(19)

y=[y1,y2, …,yn]T

(20)

B={Kij=K(xi,xj),i,j=1, 2, …,n}

(21)

式(21)中，K(xi,xj)是核函数，径向基函数具有良好的跟踪性能，比较适用于软测量建模[15]，其形式如式(22)所示：

(22)

式中：σ——核函数的带宽。

根据式(17)求解得最终的决策函数如式(23)所示：

(23)

因为最小二乘支持向量机只求解线性方程，所以它的求解速度比支持向量机更快。

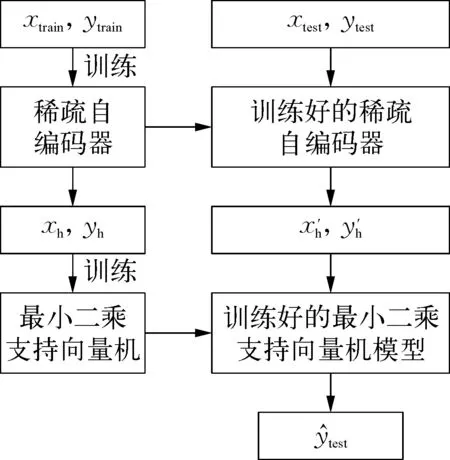
图3 软测量建模流程示意

3 仿真实验

青霉素发酵过程的输出变量是青霉素浓度，仿真所用的数据利用PenSim软件获得。PenSim是为青霉素发酵过程设计的仿真软件，该软件是由伊利诺伊科技学院的过程建模、监测及控制研究小组基于Birol模型开发的，该软件可实现青霉素发酵过程的一系列仿真[16]。PenSim软件实现的青霉素发酵过程仿真中会生成18种过程变量，仿真数据可通过对初始值的设定获得。PenSim软件的部分初始条件见表1所列。

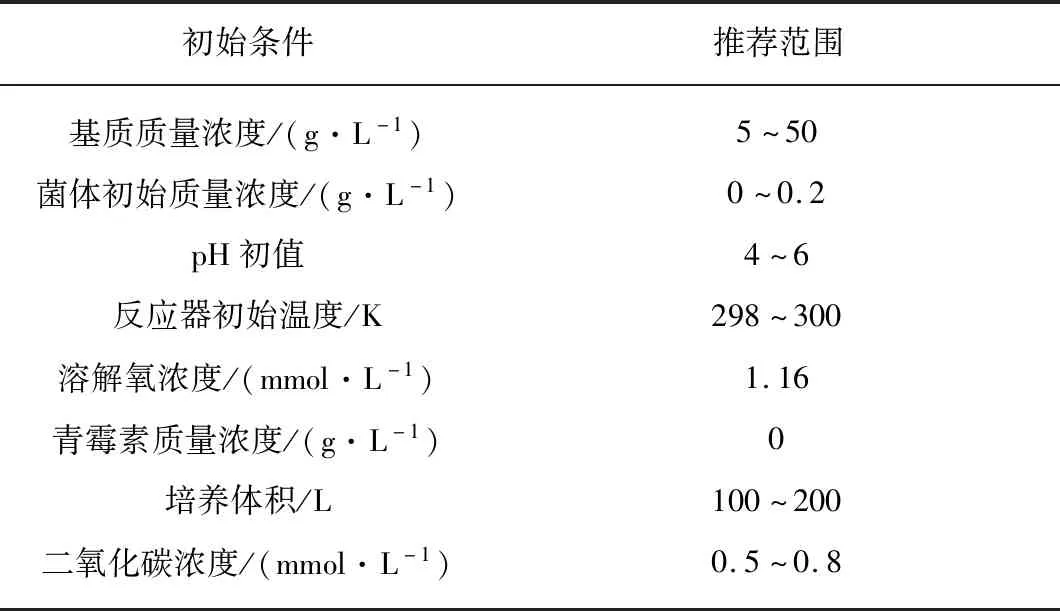
表1 PenSim软件部分初始条件

本文设定青霉素发酵的反应时间和采样时间分别为400 h和1 h，因此共生成400组仿真数据，选取前300组作为训练数据，后100组作为测试数据。通过k-近邻互信息计算出的各输入变量与青霉素浓度的相关性，见表2所列。

表2 输入变量与青霉素浓度的相关性

本文提取出与青霉素浓度相关性较大的11个变量作为建模的辅助变量，包括菌体浓度、基质体积、二氧化碳浓度、补料温度、基质浓度、溶解氧浓度、补料率、通风率、鼓风机功率、生成热和pH值。然后利用稀疏自编码器对辅助变量和青霉素浓度提取特征值，最后利用最小二乘支持向量机建模。

为了对比分析，利用互信息同样提取出11个辅助变量，包括时间、生成热、菌体浓度、二氧化碳浓度、基质体积、补料率、溶解氧浓度、生成氧浓度、补料温度、基质流速和鼓风机功率。同样利用稀疏自编码器提取特征值，利用最小二乘支持向量机建模。两种方法的仿真结果如图4和图5所示。

从图4，图5中可以看出，利用k-近邻互信息选择辅助变量的仿真效果比只用互信息选择辅助变量的仿真效果更好。但是为了使软测量建模更加简便，继续对辅助变量降维，选择包括菌体浓度、基质体积、二氧化碳浓度和补料温度在内的4个变量作为辅助变量，剔除了基质浓度、溶解氧浓度、补料率、通风率、鼓风机功率、生成热和pH值。其仿真结果如图6所示。

图4 利用互信息的仿真结果示意

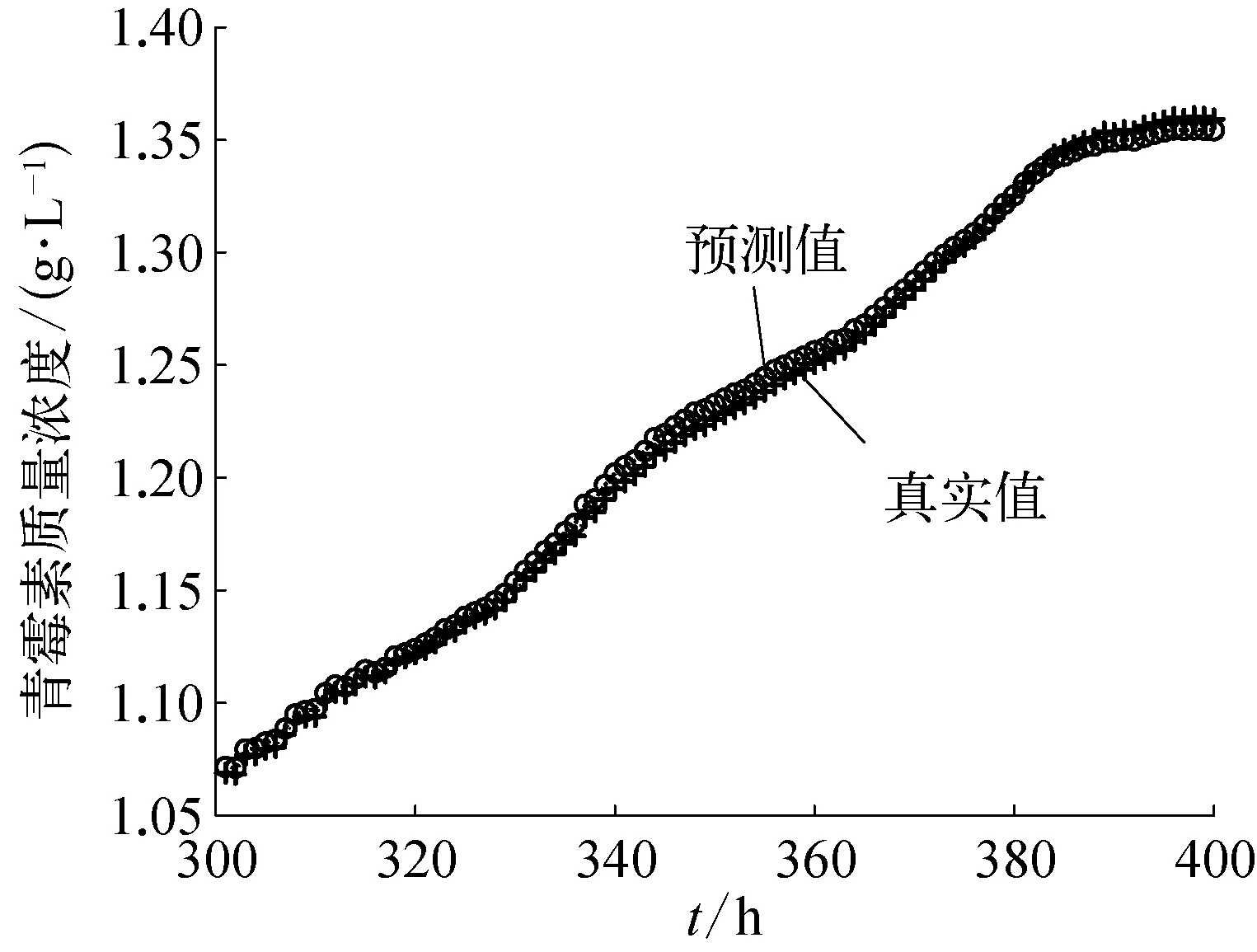
图5 利用k-近邻互信息的仿真结果示意

图6 降维后的仿真结果示意

从图6中可以看出，当选择4个变量作为辅助变量时，预测效果良好。但是经过仿真验证，当对辅助变量继续降维时，其模型的仿真结果变差，因此不再继续降维。

4 结束语

以青霉素发酵过程为背景，通过k-近邻互信息选择4个变量作为辅助变量，通过稀疏自编码器提取特征值，并用于最小二乘支持向量机的建模，最后比较预测出的特征值和真实的特征值。与此同时，比较仅用互信息选择辅助变量的方法，以及选择11个变量作为辅助变量，可知基于k-近邻互信息选择4个变量作为辅助变量，结合稀疏自编码器和最小二乘支持向量机建模的方法，其预测效果良好。也就是说菌体浓度、基质体积、二氧化碳浓度和补料温度对青霉素浓度影响较大。