带电粒子在恒定电磁场中的运动规律探析*
白雪,李彦琦,王智秀,郑勤红
(云南师范大学 物理与电子信息学院,云南 昆明 650500)
在物理学、材料学和电工电子技术的许多研究领域都涉及带电粒子在恒定电磁场中的运动问题,但由于带电粒子在电磁场中一般做曲线运动,其运动轨迹较为复杂,运动方程的表达式也较为复杂,所以在大学物理教材及相关文献中一般仅讨论带电粒子在某些特殊恒定电磁场中的运动规律[1-4].本文利用复数变换,将带电粒子在恒定电磁场中的运动微分方程简化为简单且容易求解的微分方程,再对运动微分方程进行积分,获得带电粒子在任意恒定电磁场中的运动方程的解析解,并运用MATLAB模拟仿真带电粒子的运动轨迹,讨论其运动规律和运动特征.
1 带电粒子在恒定电磁场中的运动
1.1 恒定电磁场中带电粒子运动方程的解析解

图1 带电粒子在恒定电磁场中的运动Fig.1 Charged particle moving in a steady-state electromagnetic field
设带电粒子以初速度v0(远低于光速)斜射入任意均匀恒定电磁场中,如图1所示建立坐标系.为讨论问题方便,将磁场B的方向取为z轴正向,电场位于yoz平面内,电场强度E的方向与z轴正向的夹角为α,带电粒子初速度v0与z轴正向的夹角为β,初速度v0在xoy平面的投影分量与x轴正向的夹角为γ,入射点的位置坐标为(x0,y0,z0).
由于粒子沿z轴方向的初速度分量vz0=v0cosβ,沿x轴方向的初速度分量vx0=v0sinβcosγ,沿y轴方向的初速度分量vy0=v0sinβsinγ;电场沿z轴方向分量Ez=Ecosα,沿y轴方向分量Ey=Esinα,根据牛顿第二定律,粒子所受的合力及其运动方程为
F=qv0×B+qE=ma.
(1)
粒子在三个坐标轴方向的运动微分方程为
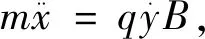
(2)
(3)
(4)
对(4)式积分,利用初始条件可得带电粒子沿着z轴方向的速度分量为
(5)
对(5)式积分,再利用初始条件可得带电粒子沿着z轴方向的坐标为
(6)

(7)
(8)
由(7)和(8)式可得
整理后可变为
(9)
将C1值代入(9),由欧拉公式可得
(10)
由于
所以粒子沿x方向的速度分量为
(11)
粒子沿y轴方向的速度分量为
(12)
对(10)式积分可获得粒子沿x轴方向的坐标为
(13)
对(11)式积分可获得粒子沿y轴方向的坐标为
(14)
将(13)和(14)式进一步整理可得
(15)
(16)

1.2 带电粒子在恒定电磁场中运动轨迹的理论探析
令
代入式(6)、(15)和(16)可得带电粒子在恒定电磁场中的运动方程为
(17)
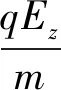
1.2.1 带电粒子斜射入恒定磁场和平行电磁场的运动方程
(1)当电场E=0,带电粒子以任意初速度斜射入恒定磁场时,由(17)式可得带电粒子的运动方程为
(18)

(2)当Ey=0,带电粒子斜射入恒定平行电磁场时[4],由(17)式可得带电粒子的运动方程为
(19)

1.2.2 带电粒子垂直射入正交恒定电磁场的运动方程
当vz0=0,Ez=0,带电粒子斜射入正交恒定电磁场时[1],由式(17)可得该条件下带电粒子的运动方程为
(20)
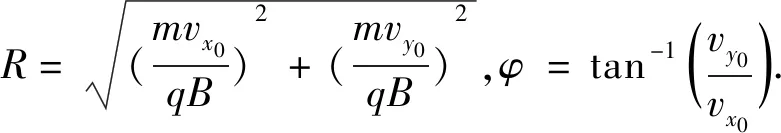
2 基于MATLAB的带电粒子运动轨迹演示与分析
取粒子所带的电荷量q为1.6×10-19C,质量m=2×10-19kg,利用MATLAB进行仿真.
2.1 带电粒子斜射入恒定磁场
当带电粒子从坐标原点斜射入恒定磁场时,设粒子初速度v0=5 m/s,E=0,B=1 T,α=0,β=π/3,γ=π/6.带电粒子运动轨迹仿真结果见图2(a);粒子运动轨迹在yoz平面的投影见图2(b).由图2可知,粒子沿z轴方向做螺距不变的螺旋运动.
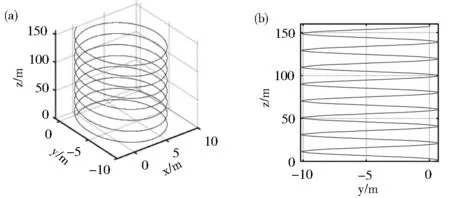
图2 带电粒子斜射入恒定磁场的(a)运动轨迹和(b)运动轨迹在yoz平面的投影Fig.2 The motion trajectory(a) and its yoz planar projection(b) of charged particle shooting obliquely into a steady-state magnetic field
2.2 带电粒子斜射入同向恒定电磁场
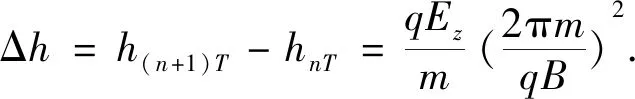
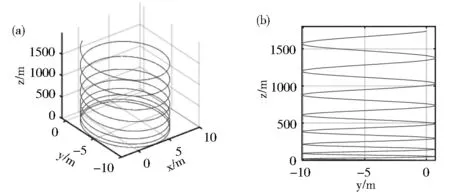
图3 带电粒子(q>0)斜射入恒定同向电磁场的(a)运动轨迹和(b)运动轨迹在yoz平面的投影Fig.3 The motion trajectory(a) and its yoz planar projection(b) of charged particle(q>0) shooting obliquely into a steady-state co-directional electromagnetic field


图4 带电粒子(q<0)斜射入恒定同向电磁场的(a)运动轨迹和(b)运动轨迹在yoz平面的投影Fig.4 The motion trajectory(a) and its yoz planar projection(b) of charged particle(q<0) shooting obliquely into a steady-state co-directional electromagnetic field
2.3 带电粒子射入正交恒定电磁场
当带电粒子从坐标原点斜射入恒定正交电磁场时,设粒子初速度v0=5 m/s,E=1 N/C,B=1 T,α=π/2,β=π/3,γ=π/6.带电粒子运动轨迹仿真结果见图5(a).带电粒子的运动轨迹在xoy平面内的投影见图5(b),为长幅摆线[1],带电粒子沿z方向的运动见图5(c),为匀速直线运动,因此该条件下带电粒子的运动轨迹为三维空间中的摆线.
2.4 带电粒子射入非正交恒定电磁场
当带电粒子斜射入非正交恒定电磁场时,设粒子初速度v0=5 m/s,E=1 N/C,B=1 T,α=π/3,β=π/3,γ=π/6.带电粒子运动轨迹仿真结果见图6(a);带电粒子的运动轨迹在xoy平面内的投影见图6(b),为长幅摆线[1];带电粒子沿z轴方向的运动曲线见图6(c),为匀加速运动曲线;因此带电粒子的运动轨迹为三维空间中的螺旋曲线[4].
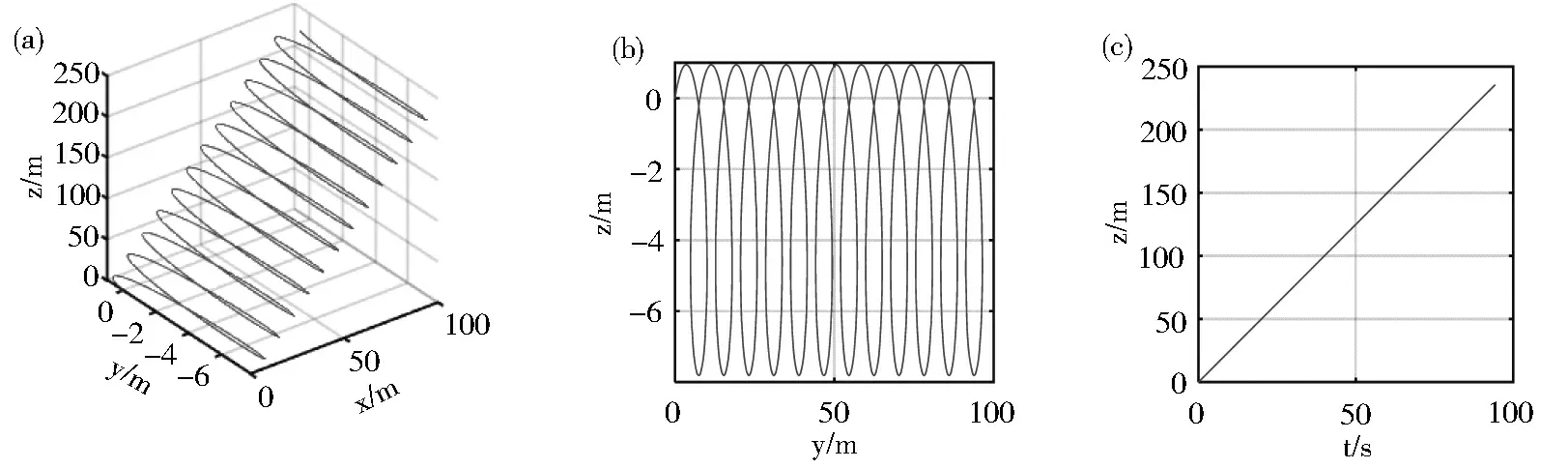
图5 带电粒子斜射入恒定正交电磁场的(a)运动轨迹、(b)运动轨迹在xoy平面的投影和(c)粒子沿z方向的运动Fig.5 The motion trajectory(a),its xoy planar projection(b),and the motion in z-direction(c) of charged particle shooting obliquely into a steady-state orthogonal electromagnetic field
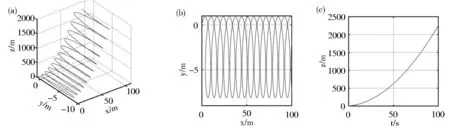
图6 带电粒子斜射入恒定非正交电磁场的(a)运动轨迹、(b)运动轨迹在xoy平面的投影和(c)粒子沿z方向的运动Fig.6 The motion trajectory(a),its xoy planar projection(b),and the motion in z-direction(c) of charged particle shooting obliquely into a steady-state non-orthogonal electromagnetic field
分析比较带电粒子斜射入正交恒定电磁场和非正交恒定电磁场的运动轨迹可知,两种条件下其运动轨迹都是复杂的空间螺旋曲线,这两种运动轨迹在xoy平面的投影都是摆线,但射入非正交恒定电磁场的粒子沿z轴方向做匀加速直线运动,斜射入正交电磁场的粒子沿z轴方向做匀速直线运动,两者沿z轴方向分运动的不同导致两者合运动的轨迹差异非常大.
3 结果与讨论
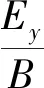
基于MATLAB的带电粒子运动轨迹演示与分析结果表明,带电粒子在任意恒定电磁场中的运动可分为两大类(除匀速圆周运动和直线运动外):(1)螺旋运动.当带电粒子在xoy平面内只参与了匀速圆周运动,在z方向参与了匀速直线运动或匀变速直线运动,带电粒子的运动为螺旋运动.若带电粒子沿z方向有匀速直线运动,则粒子的运动为螺距不变的螺旋运动(例如:当带电粒子斜射入恒定磁场时);若带电粒子沿z方向参与了匀变速直线运动,则带电粒子的运动是螺距随时间变化的螺旋运动(例如:当带电粒子斜射入恒定平行电磁场时).(2)复杂螺旋运动.当带电粒子在xoy平面内做匀速圆周运动和沿x轴方向做匀速直线运动,且在z轴方向做匀速直线运动或匀变速直线运动,带电粒子的运动轨迹为复杂的空间螺旋曲线(例如:带电粒子斜射入正交电磁场或射入非正交电磁场时);当带电粒子的入射速度v0、电场强度E和磁场B三者之间相互垂直时,带电粒子的运动轨迹相对简单,其运动轨迹为xoy平面内的摆线.

