隔震桥梁模型更新混合试验数值模拟

孟丽岩， 刘 媛， 王 涛

(黑龙江科技大学 建筑工程学院， 哈尔滨 150022)

0 引 言

桥梁结构的减隔震设计是目前备受关注的一项防震技术，国内外学者对桥梁结构减隔震技术进行了大量理论分析和试验研究。Wang等[1]提出了适用于强非线性结构系统的动力分析方法，对装有减隔震支座的桥梁进行了动力响应分析。Tsopelas等[2]通过装有E型钢阻尼器的减震桥梁地震响应分析，讨论了减震装置对脉冲型地震动的敏感性。韩强等[3-5]通过地震模拟振动台试验研究了不同抗震设防烈度下隔震桥梁的地震动态响应，得出了隔震桥梁体系隔震效果影响因素。袁涌等[6]通过实时子结构试验分析了具有不同速度相关型的隔震支座对桥梁结构地震影响。然而，现代桥梁体量庞大、结构复杂，传统抗震试验方法难以满足检验大型桥梁抗震性能的要求。模型更新混合试验方法是一种将物理试验和数值模拟相结合，并对数值模拟部分进行模型更新的结构抗震试验方法，可以避免振动台试验“尺寸效应”问题，有效提高结构抗震试验结果准确性。在线模型更新精确度是影响试验结果的关键环节，为了进一步提高强非线性模型参数在线识别精度，王涛等[7-8]提出一种改进的辅助无迹粒子滤波(Auxiliary unscented particle filter，AUPF)算法，AUPF算法在粒子滤波(Particle filter，PF)算法的基础上主要进行了两方面改进，采用无损卡尔曼滤波(Unscented Kalman filter，UKF)算法进行重要性采样和在重采样过程中引入辅助因子修改粒子权值，提高非线性系统粒子更新精确度，通过增加粒子多样性削弱了粒子退化现象。笔者采用OpenSees软件建立三跨隔震桥梁数值模型，通过Matlab编写AUPF算法对隔震支座进行模型更新，研究三种不同类型场地的地震激励下桥梁结构模型更新混合试验仿真，并与采用纯数值模拟得到的隔震桥梁真实响应进行对比。

1 桥梁模型的建立与求解

文中采用了文献[9]中的三跨连续桥梁结构，如图1所示，隔震桥梁结构包括上部结构、连接支座、桥墩和桥台、基础等。桥长70 m，跨度分别为20、30和20 m。主梁为箱型截面，采用C50混凝土；桥墩为2 m×1.2 m矩形截面，采用C30混凝土。 桥墩和上部结构之间装有聚四氟乙烯滑板橡胶支座。采用OpenSees软件进行隔震桥梁结构地震反应分析，上部结构采用弹性梁单元模拟；桥墩单元采用基于柔度法的弹塑性纤维梁单元模拟，其中无约束混凝土及约束混凝土均采用基于Kent-Park单轴混凝土模型，纵向钢筋采用Menegotto和Pinto建议模型；桥台处支座简化为理想滑动支座，中间橡胶支座采用非线性弹簧单元模拟。不考虑基础及边界条件对桥梁抗震相互影响，墩底采用固定边界条件[9]。

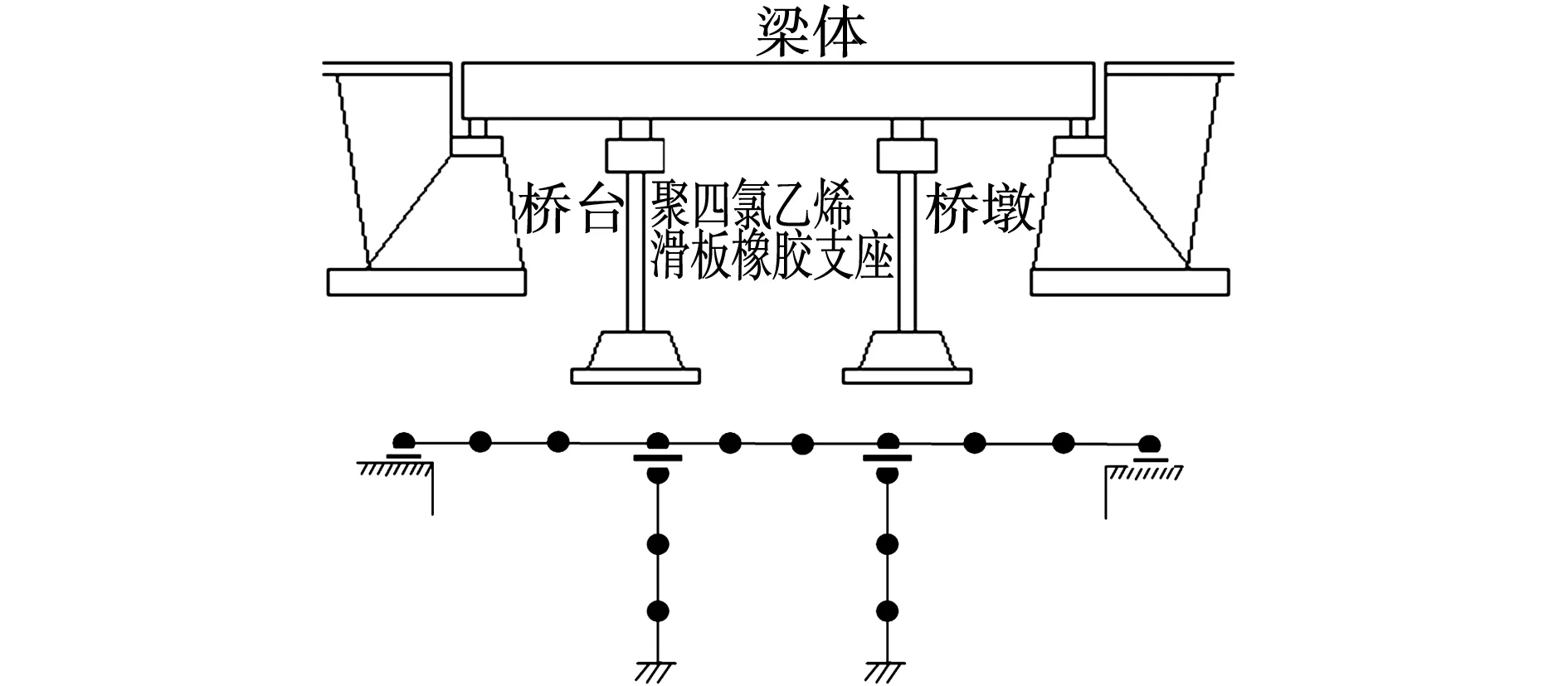
图1 隔震桥梁结构示意Fig. 1 Schermatic of seismic isolated bridge

模型采用最常用的Newmark-β增量法求解结构动力学方程，积分参数取α=1/2、β=1/4。

2 模型更新

采用OpenSees有限元软件建立桥梁模型，在Tcl编程软件中定义桥梁结构的几何参数、节点坐标、约束边界条件、节点质量、材料截面属性参数及单元类型，然后定义输入地震动，设定输出节点和单元信息。采用文献[10]中改进的OpenSees程序，实现OpenSees数值子结构模型参数实时更新。OpenSees模型更新实现方法如图2所示。在结构混合试验过程中，采用Matlab编写AUPF算法，在线识别隔震支座模型参数，然后更新OpenSees数值模型中隔震支座模型参数，进行下一步分析计算。

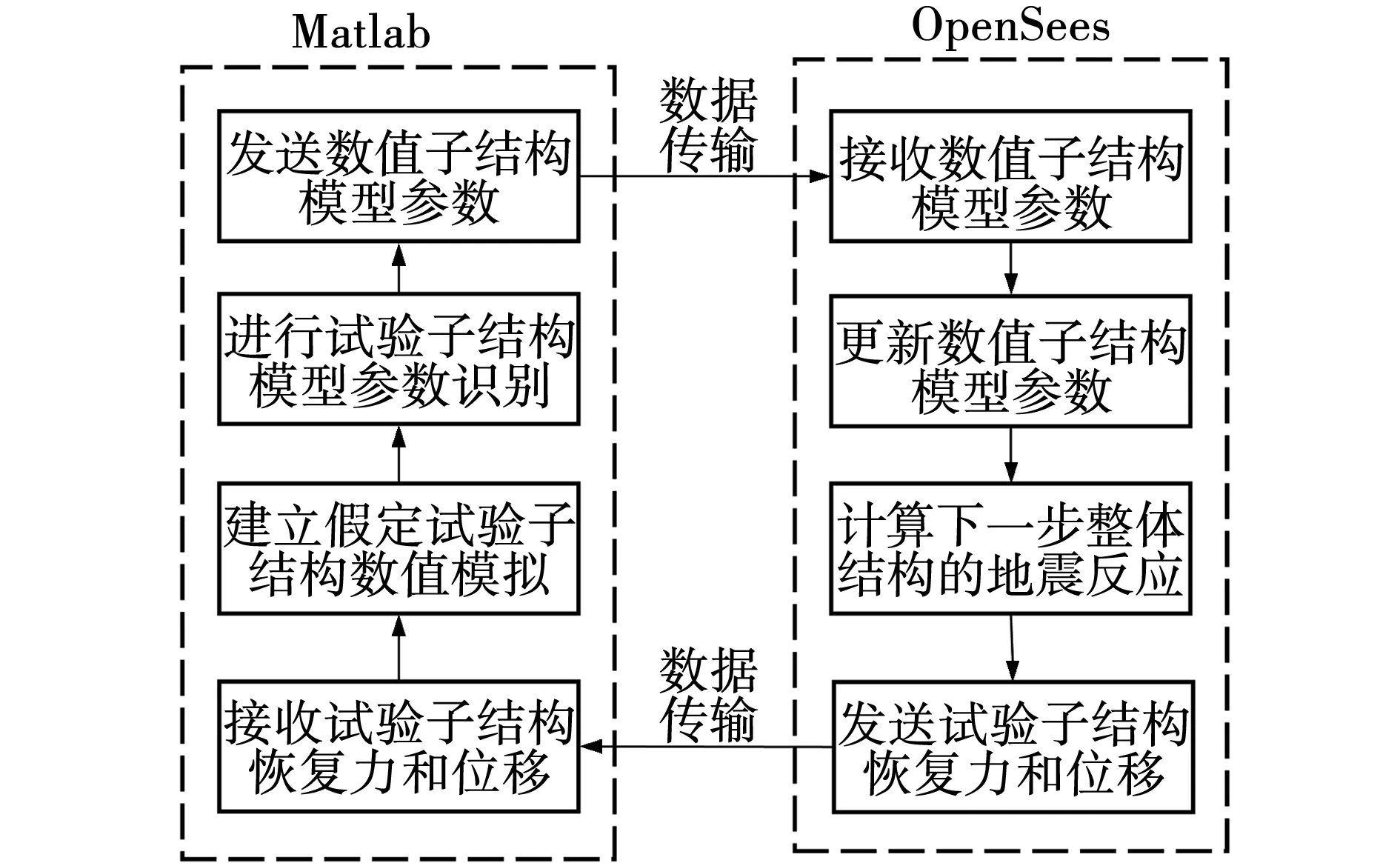
图2 OpenSees模型更新实现方法Fig. 2 Model updating method in OpenSees software

文中桥梁结构模型设为三维模型，每个节点有6个自由度，利用two Node Link单元模拟桥梁模型中的滑板式橡胶支座，并实现two Node Link单元在线数值模型更新功能。隔震桥梁结构模型更新混合试验模拟方法示意如图3所示。

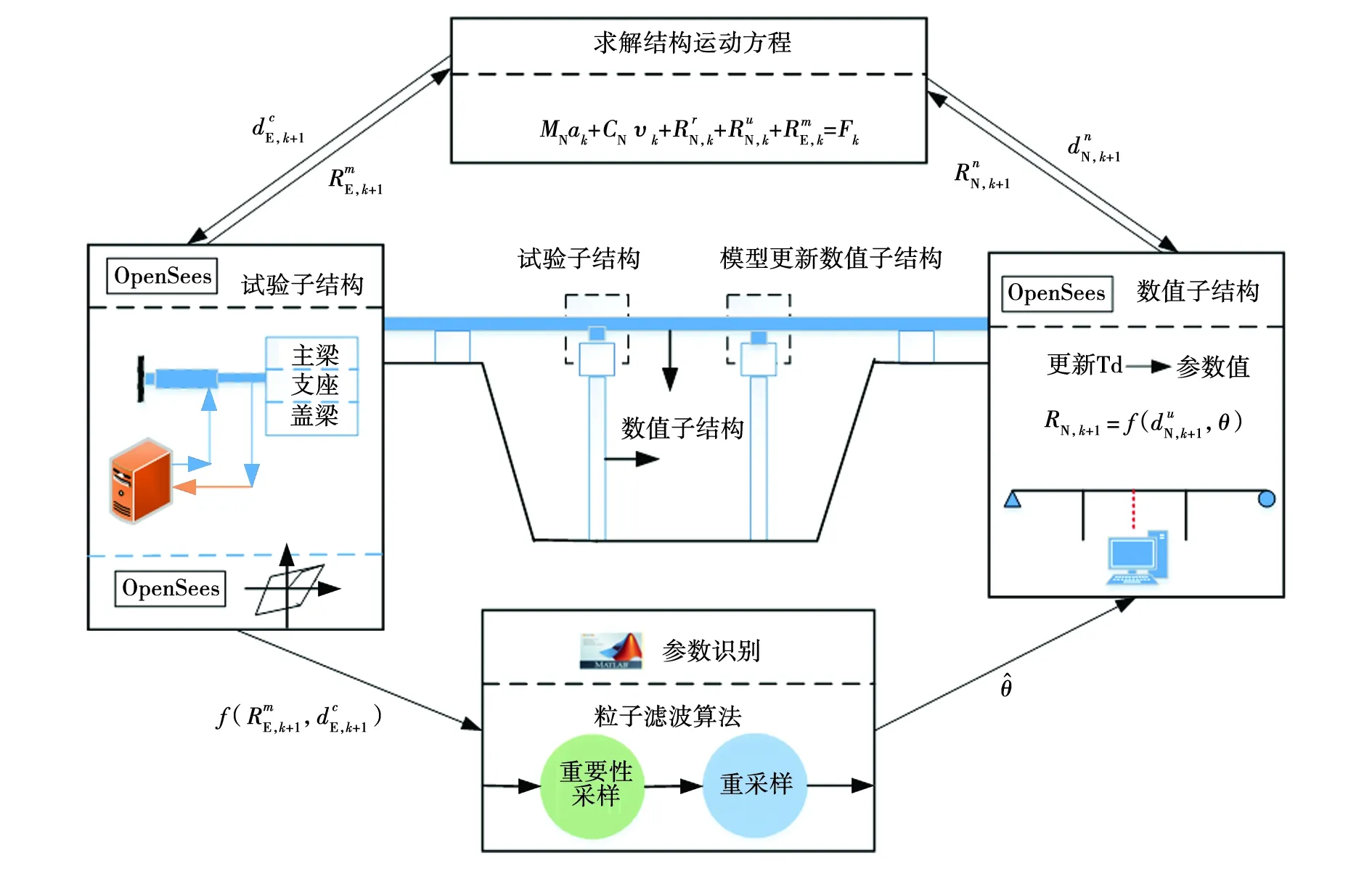
图3 隔震桥梁结构模型更新混合试验数值模拟Fig. 3 Numerical simulation of hybrid testing with model updating for seismic isolated bridge

3 三跨隔震桥梁结构算例分析

3.1 模型参数设置

在混合试验仿真中，数值子结构和试验子结构均通过OpenSees有限元软件进行数值模拟。支座在桥梁体系中起重要作用，本身力学性能复杂，因此，选取左侧支座作为试验子结构，右侧支座作为数值子结构。假定试验支座和数值支座采用相同的双折线模型，模型参数包括屈服力Fy、第一刚度k1、第二刚度与第一刚度比值α。对数值子结构支座的双折线模型设置不同参数，进行两种工况试验模拟。

(1)参考试验模拟：左右两侧支座的双折线模型参数均采用真实值，Fy=495 kN、k1=74 000 kN/mm、α=5×10-4，试验结果称为“真实值”；

(2)基于AUPF模型更新混合试验模拟：左右两侧支座均采用双折线模型，左侧支座作为试验支座，采用参数真实值，基于试验支座的力和变形观测数据，采用AUPF算法在线识别双折线模型的3个参数Fy、k1和α，同时更新OpenSees中数值支座的双折线模型参数。假定数值支座参数初始猜测值为Fy=450 kN、k1=65 000 kN/m、α=10-4，将此试验结果称为“更新值”。其中：AUPF算法的过程噪声协方差矩阵为Qt=diag(10-710-710-710-7)；观测噪声协方差为Wt=6.25 kN2；初始状态估计误差协方差为P0=diag(10-410910-1340)[2]。

3.2 模型更新参数识别结果

桥梁右侧支座的双折线模型参数在线识别值如图4所示。参数识别值从初始值快速逼近参数真实值。双折线模型参数识别终值见表1。

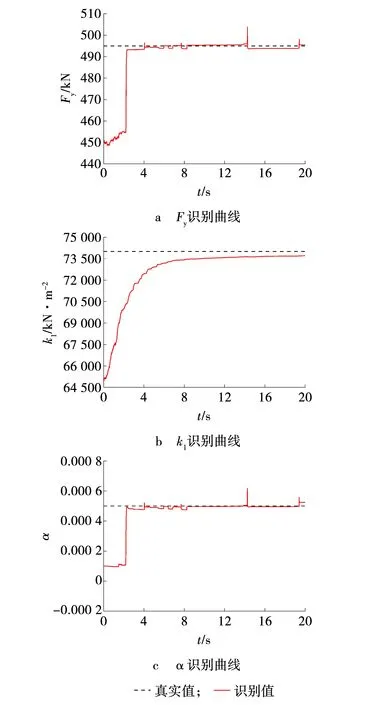
图4 双折线模型参数识别值Fig. 4 Parameter identification value of double line model

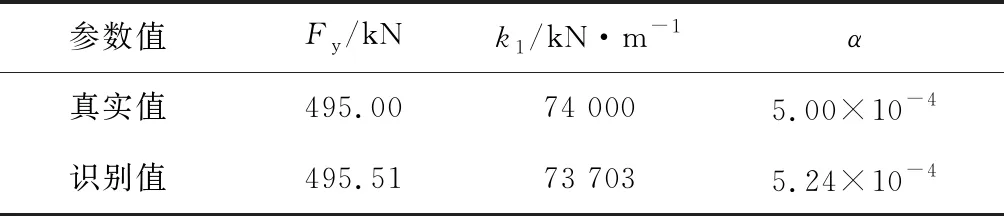
表1 双折线模型参数识别终值

结果表明：屈服力Fy识别值相对误差为0.1%，第一刚度k1识别值相对误差为0.4%；第二刚度与第一刚度比值α识别值相对误差为4.8%。可见，AUPF算法在无模型误差的情况下具有良好的非线性模型参数识别精度。

图5为上述三跨隔震桥梁模型隔震支座的滞回曲线对比图，文中桥梁支座的滞回曲线为双折线模型。从试验结果可见采用AUPF算法识别滞回曲线具有良好的双折线滞回特性，同真实值相比具有较高的相似度。

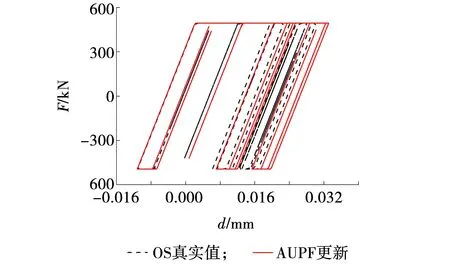
图5 隔震支座滞回曲线Fig. 5 Hysteretic curve of isolation bearing

3.3 桥梁地震响应分析结果

从地震灾害研究中可以发现，在地质软硬条件不同的工程场地上，结构即使在相同地震作用下发生毁损的情况也可能完全不同，所以通常在进行桥梁抗震分析时，针对不同场地类别也会得到不同的分析结果。文中选取了适应三类不同场地土特点的3条典型的强震加速度记录作为地震激励，包括适合Ⅰ类场地土的Cape Mendocino地震记录、适合Ⅱ类场地土的Kobe地震记录和Ⅲ类场地土的Taft地震记录，各地震记录的基本特性如表2所示。

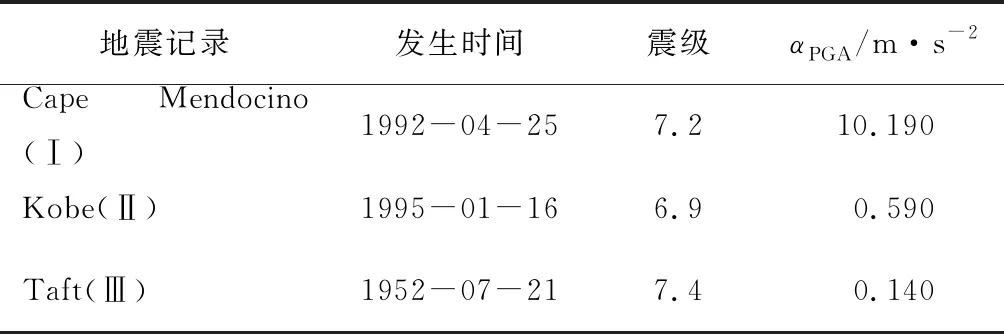
表2 地震记录的基本特征

按照9度设防烈度，将地震记录的峰值加速度αPGA(m/s2)均调整到0.40 g。对建立的三跨隔震桥梁模型分别输入Cape Mendocino、Kobe、Taft地震记录并进行桥梁地震时程分析，在支座刚度取为100 000 kN/mm时，桥梁的墩顶位移时程曲线、支座位移时程曲线、墩底剪力时程曲线以及墩顶加速度时程曲线如图6～8所示。

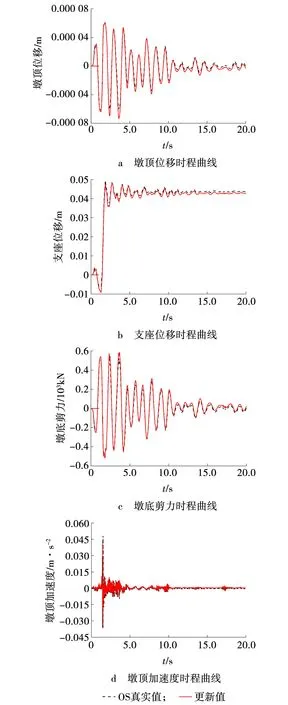
图6 Cape Mendocino激励下桥梁地震响应时程Fig. 6 Seismic response time history of bridge under Cape Mendocino excitation

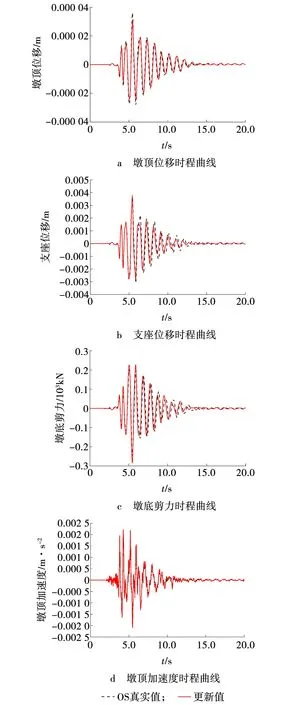
图7 Kobe激励下桥梁地震响应时程Fig. 7 Seismic response time history of bridge under Kobe excitation

由图6～8可以看出，进行模型参数更新的结构地震响应同真实模拟吻合程度较高，说明模型更新混合试验模拟方法能够大大提高抗震试验的准确性，有效降低传统抗震试验中存在的模型误差。

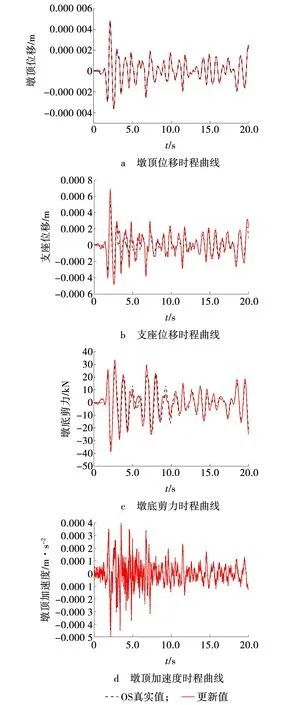
图8 Taft激励下桥梁地震响应时程Fig. 8 Seismic response time history of bridge under Taft excitation

通过墩顶加速度和墩底剪力曲线可以明显看出模型不同抗震试验模拟存在着明显误差，这种表现在Ⅰ类场地土的模拟试验中尤其显著，所以在进行Ⅰ类场地土的抗震试验分析时尤其要注意减小模型误差。

图9为Cape Mendocino地震激励、Kobe地震激励和Taft地震激励下隔震桥梁结构墩顶位移、墩顶加速度、墩底剪力和支座位移的均方根误差。从图9可以看出，在Cape Mendocino、Kobe地震激励下墩顶加速度和墩底剪力的均方根误差相对较大；在Taft地震激励下墩底剪力和支座位移的均方根误差相对较大，但最大误差也小于2.5%。说明利用AUPF算法进行模型更新混合试验得到的模拟结果与采用OpenSees真实参数值进行整体时程分析的结果吻合良好。

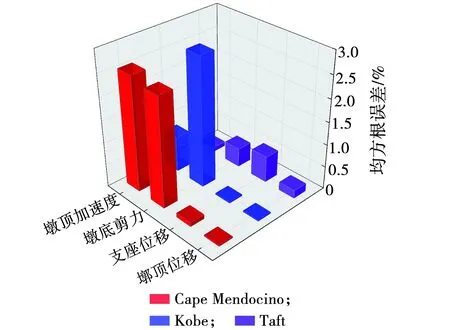
图9 三种地震激励下桥梁地震响应时程误差分析Fig. 9 Analysis of time-history error of bridge seismic response under three types of seismic excitation

4 结 论

(1)AUPF算法对于识别隔震支座的双折线模型具有良好的精度，模型参数F识别值相对误差为0.1%，k1识别值相对误差为0.4%；α识别值相对误差为4.8%。

(2)基于模型更新的隔震桥梁结构的墩顶位移、墩顶加速度、墩底剪力和支座位移时程与参考试验模拟的结果吻合良好，其中Cape Mendocino地震激励下墩顶加速度均方根误差最大，小于2.5%，试验模拟精度较高，有利于进行大型复杂桥梁的地震反应分析。