非均匀Halbach阵列涡电流分选机的磁辊模态

吕 品， 李明军， 翟悦林， 程鲁帅， 王凯旋， 王浩铭

(黑龙江科技大学 电气与控制工程学院， 哈尔滨 150022)

0 引 言

2021年1月以来，铜价同比增长60%，进口铜废碎料364 000吨，同比增长73%，可见我国对有色金属需求量大且回收能力有待提升。涡电流分选机是从有色金属及非金属混合物料中分选有色金属的环保型设备，具有结构简单、绿色节能等特点而被广泛应用于有色金属回收领域[1]。涡电流分选技术被广泛应用于矿业矿石分选领域，是一种可行且实用粗金回收浓缩技术，在矿业工程方面具有良好应用前景[2]。因此，现阶段对涡电流分选机研究具有较高理论研究意义和工程应用价值。

涡电流分选机的研究始于20世纪70年代，其设计追求低振动与高功率密度。涡电流分选机磁辊结构模态分析是抑制其振动的关键，而提高永磁设备的功率密度，主要措施为提高永磁体利用率[3]。为增大涡电流分选效率，国内外学者设计了多个涡电流分选机方案，包括双磁辊方案、新磁极结构等[4-7]。2021年，Halbach阵列磁化方案应用于涡电流分选机永磁体磁辊，大幅增大了涡电流分选机磁辊周围磁感应强度幅值，提高了永磁体利用率[3]。而涡电流分选机不断改进过程中，其分选涡电流电磁力逐渐增大，可分选有色金属尺寸逐渐增大，作业过程中磁辊结构载荷逐渐增加，长期运行使磁辊轴系振动对其结构稳定性产生影响，磁辊结构固有频率和对应振型计算是磁辊轴系振动研究基础[8]。

有色金属与非金属的分离依赖于磁辊与有色金属块之间的涡电流电磁力，可以视为磁辊磁场产生磁通与有色金属内部感生磁通相互的作用，这与电机内部定、转子间电磁力关系十分相似。通过分析电机电磁噪声与振动，学者们得出了抑制共振的有效措施为确保电机结构各阶固有频率高于其受到涡电流电磁力波频率的结论[9]，预测分析电机结构各阶固有频率为抑制其共振的基础[10-11]。黄梓嫄等[12]通过修正刚度因子，实现对电机柔性转子系统模态的精确分析。林展毅等[13]以高速电机永磁转子为研究对象，分析了转子各个部件应力与转子动力学特性。涡电流电磁力的谐波分量频率高于磁辊固有频率条件下，可能导致磁辊结构产生共振，甚至破坏轴承，影响涡电流分选机的安全稳定运行，造成巨大经济损失甚至影响人身安全。因此，对涡电流分选机磁辊结构的模态分析是保证涡电流分选机稳定运行的关键，值得深入研究。为避免磁辊共振，应避免涡电流电磁力波频率高于磁辊结构固有频率，而有色金属的质量、电导率等因素对涡电流电磁力频率无影响[14]，且由于有色金属尺寸远小于磁辊尺寸，忽略有色金属尺寸对涡电流电磁力波的频率影响。

鉴于涡电流分选机磁辊模态研究的空缺，笔者在以往关于涡电流分选机研究的基础上，对磁辊结构模态分析展开研究，以一台转速为800 r/min的磁辊为研究对象，介绍涡电流分选机的运行方式及分选原理，给出描述磁辊运动的动力学微分方程，分别采用ANSYS Electronics和ANSYS Workbench有限元计算平台，建立静磁场二维电磁及三维模态有限元计算模型，在此基础上，推导涡电流分选机运行条件下，高速旋转的磁辊结构对有色金属的各阶涡电流电磁力波频率。根据有限元计算与推导结果，获取前3次径向涡电流电磁力谐波与基波幅值比。通过对比分析，给出考虑磁辊振动因素非均匀Halbach阵列涡电流分选机磁辊最佳主磁极与等效磁极角度比。

1 分选原理

涡电流分选机磁辊由永磁体磁极、磁轭与转轴组成，磁极由螺钉固定在磁轭上，各部分间紧密配合，无相对位移。磁极沿圆周排列顺序为Halbach阵列，每个等效磁极可以分为一个径向磁化的主磁极与一个切向磁化的辅助磁极。设计主磁极与辅助磁极的磁极角度不同时，磁辊的磁化阵列为非均匀阵列。涡电流分选机运行示意如图1所示。

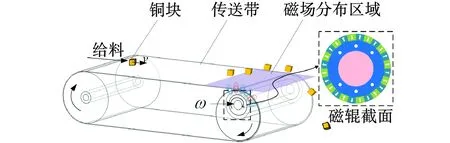
图1 涡电流分选机运行原理Fig. 1 Operation principle of ECS

由图1可见，当有色金属由给料机输送至分选机的传送带上，随传送带水平运动并逐渐靠近磁辊，当其进入磁辊上方磁场分布区域后，磁辊上方磁感应强度分为径向分量及切向分量。在旋转磁辊产生的交变磁场中，有色金属块内部磁通快速交变，金属块内部存在涡电流分布，涡电流磁通与磁辊产生磁通相互作用，金属块与磁辊之间存在涡电流电磁力，包含径向分量及切向分量，其形式为多次倍频正弦相量叠加和，其中，径向涡电流电磁力波为导致磁辊振动的关键性因素[9]。在涡电流电磁力的影响下，有色金属离开传送带时进行斜抛运动，而非金属在此过程中不受涡电流电磁力，进行平抛运动，有色金属与非金属因此分离。

采用Halbach阵列的磁辊磁极排布如图2所示。每个磁极由一个主磁极与一个辅助磁极组成，设主磁极角度为η1，辅助磁极角度为η2，则单个等效磁极角度为η=η1+η2，Halbach阵列磁辊的等效磁极数p为2π/(η1+η2)。相较于传统径向磁化磁辊，Halbach阵列磁辊可以产生近似正弦波形的磁感应强度，且幅值更大，谐波分量更少。为避免涡电流分选机运行过程中磁辊共振，探究Halbach阵列涡电流分选机磁辊的固有频率及振型是十分必要的。

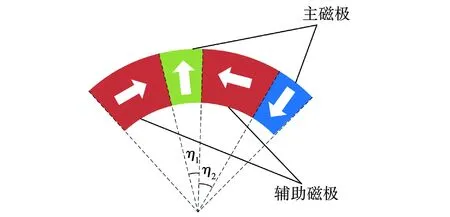
图2 磁辊磁化方案Fig. 2 Magnetization scheme of magnetic roller

2 有限元法电磁分析

2.1 磁场分析理论

静磁场有限元求解器计算磁场基于安培定律和麦克斯韦方程为

∇×H=J，

(1)

∇·B=0，

(2)

(3)

式中：H——磁场强度；

B——磁感应强度；

J——电流密度；

μr——相对磁导率；

μ0——真空磁导率。

联立式(1)～(3)，可得：

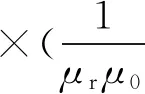
(4)

式中，A——矢量磁位。

由矢量磁位计算磁感应强度为

B=∇×A。

(5)

2.2 二维电磁有限元模型建立与求解

文中研究采用ANSYS Electronics有限元计算平台，分别建立等效磁极数目p为24、16、12的磁辊截面有限元计算模型。磁辊的永磁体磁极内径为113 mm，外径为138 mm，轴向长度为1 454 mm，传送带与夹层气隙厚度共10 mm，故有色金属颗粒距离磁辊截面圆心为148 mm。

由以上数据构建二维静磁场有限元计算模型后，求解磁辊周围磁感应强度，有限元计算采用基本运算。模型设置有限元模型的边界条件为自然边界条件，磁感应强度测量曲线为半径r=148 mm的圆周。静磁场内，不考虑有色金属内部磁感应强度分布，故不考虑透入深度，因此，剖分采用on selection-Length Based，永磁体磁极部分为主要计算区域，设置剖分最大单元长度为2 mm，内部套件和转轴最大单元长度为6 mm，外部空气最大单元长度为4 mm。等效磁极p取24、16、12极均匀Halbach阵列涡电流分选机磁辊有限元计算磁感应强度云图如图3所示。

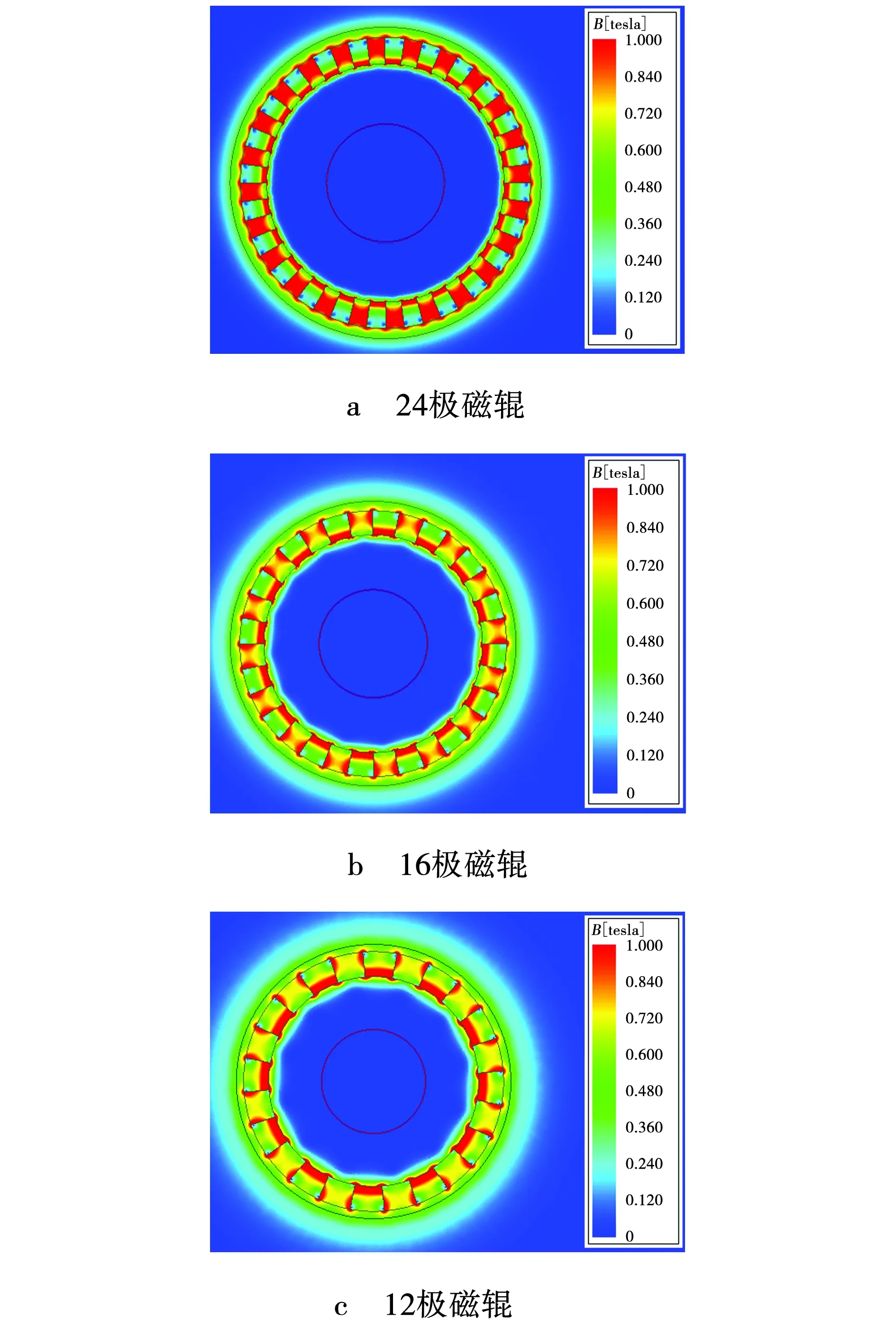
图3 磁辊截面磁感应强度分布Fig. 3 Magnetic flux intensity distribution of magnetic roller section

由图3可见，等效磁极角度分别为15°、22.5°、30°。磁辊周围磁感应强度在圆周上呈现正弦变化，且随着磁辊磁极数目减少，分布区域逐渐增大。磁辊外部磁感应强度从半径Rb处0.7 T衰减至0 T。有限元计算测量处磁感应强度波形如图4所示。磁辊外磁感应强度的径向分量与切向分量同频率，随着磁极数目减少，分量幅值逐渐增大，周期逐渐延长。

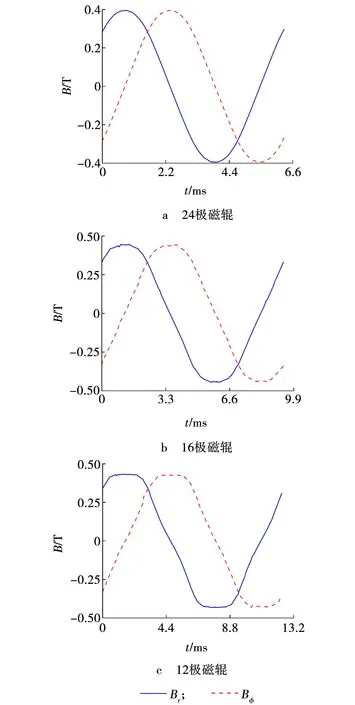
图4 有限元计算测量处磁感应强度波形Fig. 4 FEM calculation results of magnetic flux intensity waveform at measurement position

设磁感应强度的谐波幅值相对基波幅值的百分比为w，则r=148 mm测量处磁感应强度的傅里叶分解结果见图5。该磁辊外部磁感应强度径向分量及切向分量含有基波及五次谐波，五次谐波幅值小于磁感应强度基波幅值的10%，且随磁极数目减少，五次谐波的占比逐渐增加。

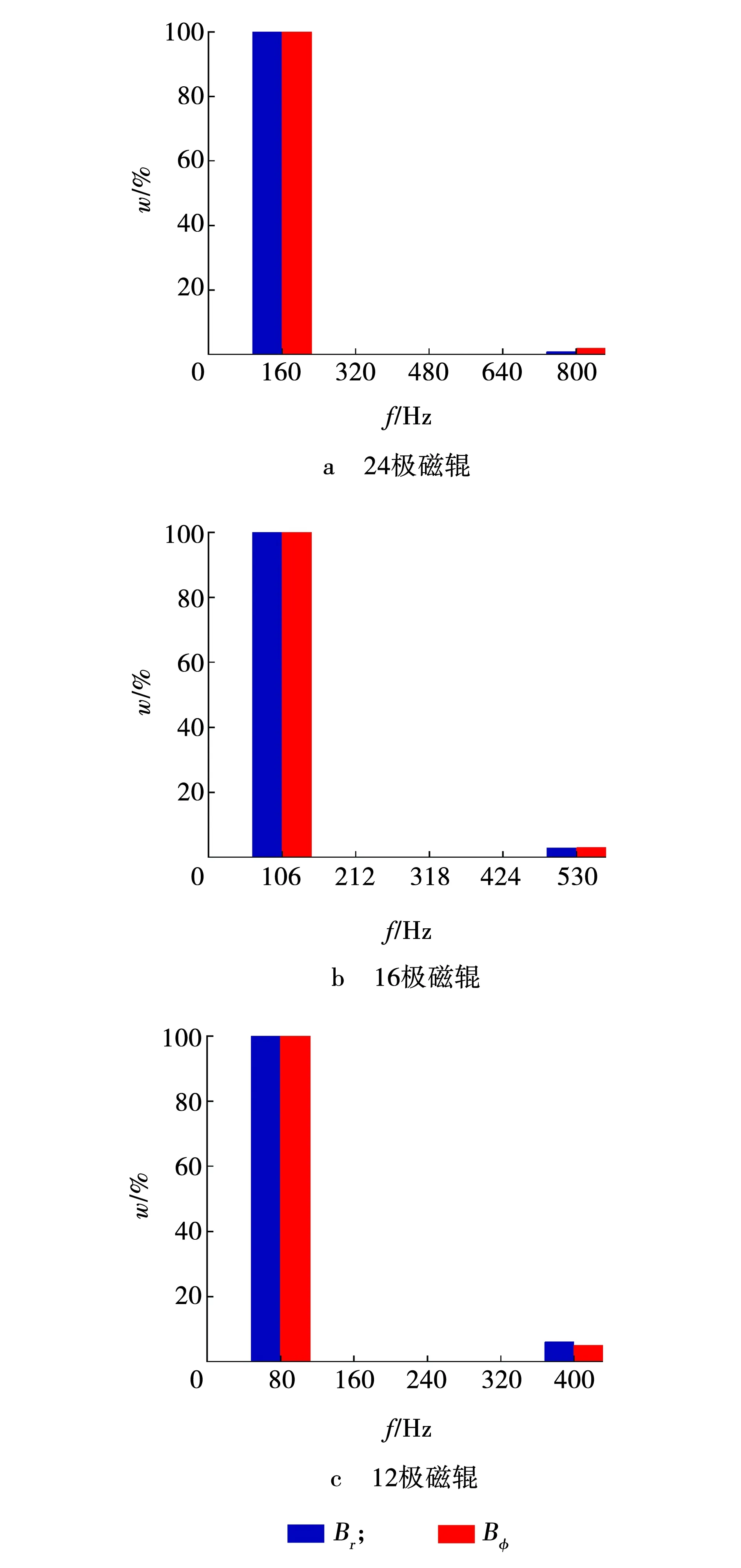
图5 测量处磁感应强度傅里叶分解结果Fig. 5 Fourier decomposition results of magnetic flux intensity at measuring position

Cao等[3]采纳Halbach阵列磁化方案，设计了主磁极与辅助磁极不等宽的非均匀磁辊结构，以增大磁辊外部磁感应强度幅值。

设计不同等效磁极角度下，Halbach阵列磁辊主磁极角度与整个磁极角度的比例M=η1/η，取不同磁极角度、主磁极占比，分别建立有限元模型计算主磁极与辅助磁极不等宽的磁辊周围磁感应强度径向分量，有限元计算结果及其傅里叶分解结果、磁辊外磁感应强度径向分量基频、各次谐波频率及谐波畸变率如表1所示。

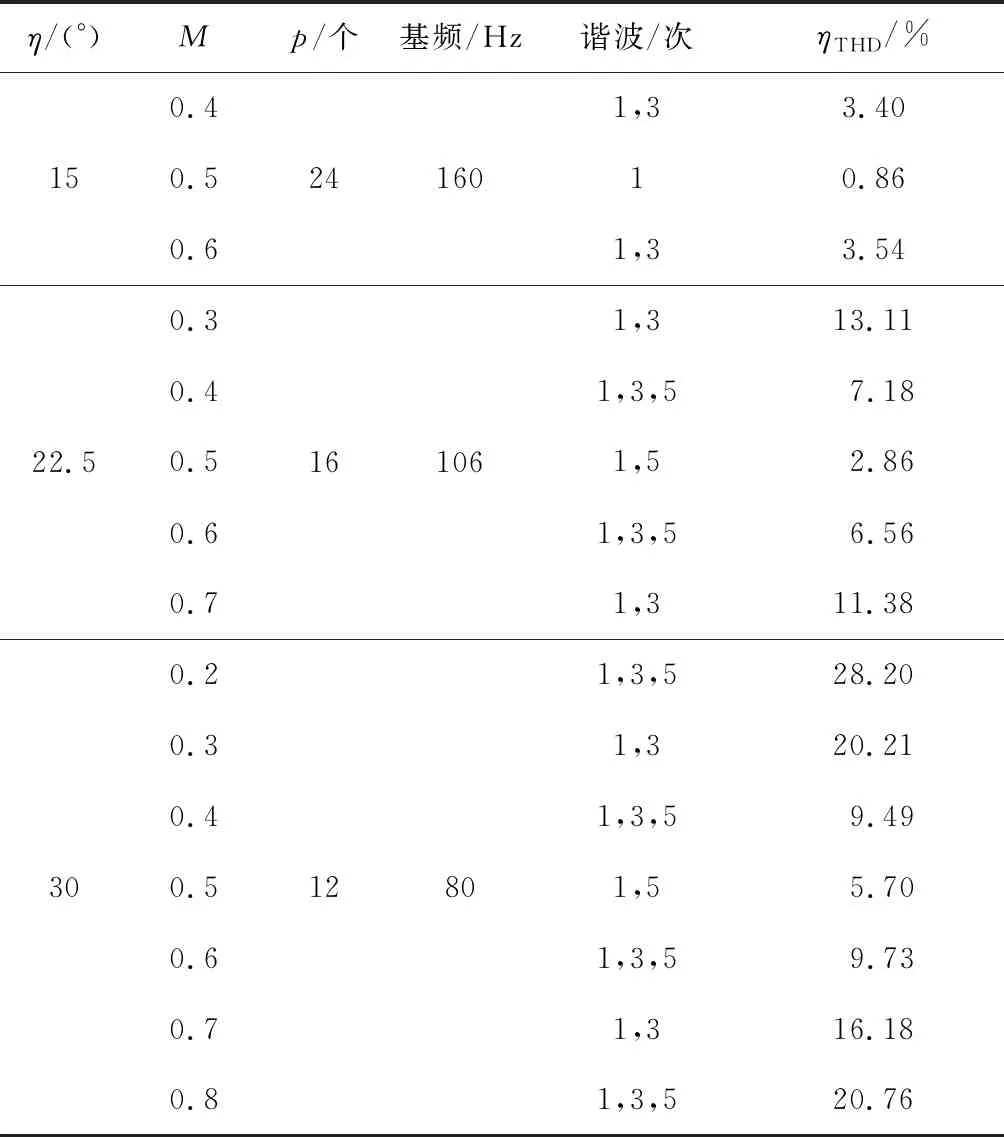
表1 磁辊磁感应强度径向分量有限元计算结果

由表1可知，更改Halbach阵列涡电流分选机磁辊的主磁极角度占比，磁辊外磁感应强度谐波含量因此而改变，主磁极与辅助磁极角度相差越大，谐波畸变率越高，成分越复杂。

3 有限元法模态分析

3.1 模态分析理论

由胡克定律可知，力矢量为

F(t)=-Kx，

(6)

式中：K——刚度矩阵；

x——位移矢量。

由牛顿第二定律

(7)

考虑弹性系统阻尼的二阶微分方程为

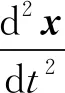
(8)

式中：M——质量矩阵；

C——阻尼矩阵。

无阻尼模态分析中，C为零矩阵，得：

(K-ω2M)x=0，

(9)

系统固有角频率为

|K-ω2M|=0。

(10)

物体的固有频率越低，越容易被外部因素激励[8]，避免磁辊结构共振的基础为磁辊结构的固有频率高于外界激励的频率。为避免磁辊共振，需分别求解非均匀Halbach阵列磁辊周围磁感应强度各次分量的频率，以及磁辊结构产生涡电流电磁力各次波形频率及磁辊结构的固有频率。

3.2 三维模态有限元模型建立与求解

磁辊材料的各项参数如表2所示。磁辊的内部材料、尺寸、结构名称如图6所示。转轴及磁轭、永磁体磁极之间物理参数相近，由于磁辊各部件之间紧密配合，将磁辊磁轭及转轴简化为磁辊转子轴。磁辊有限元模态计算模型剖分如图7所示。

表2 磁辊结构材料参数

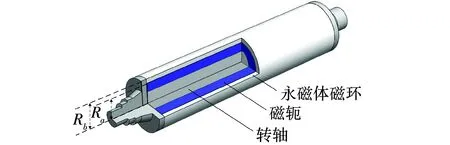
图6 永磁磁辊3/4剖面Fig. 6 Permanent magnetic roller 3/4 section

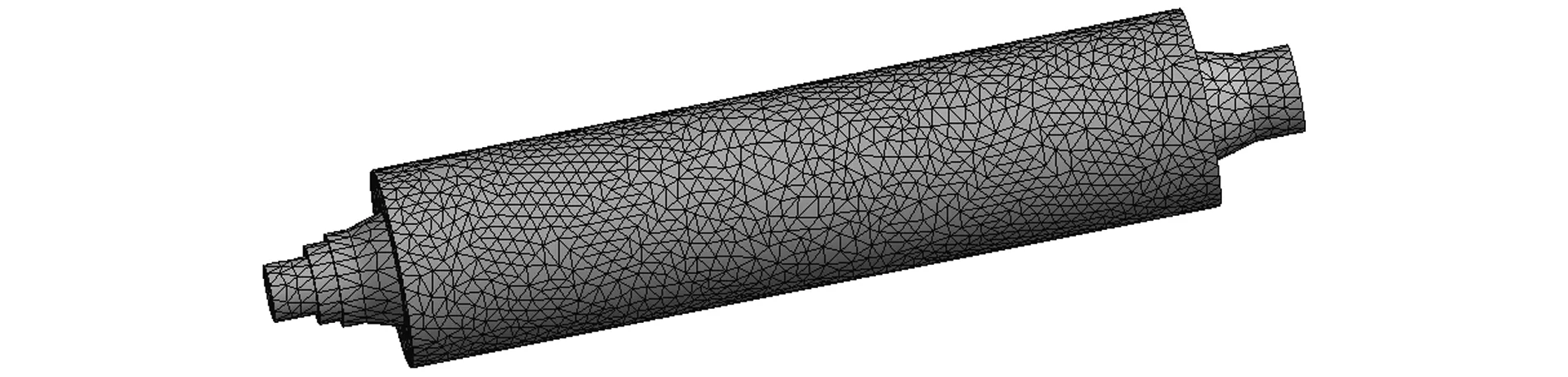
图7 磁辊剖分后模型Fig. 7 Magnetic roller model after mesh operation

由图6与表2可知，采用Solid Works软件绘制磁辊三维模型，基于转子系统有无穷多个自由度且弹性系统质量分布连续假设，采纳ANSYS Workbench软件建立有限元计算模型，涡电流分选机磁辊前6阶固有频率见图8。

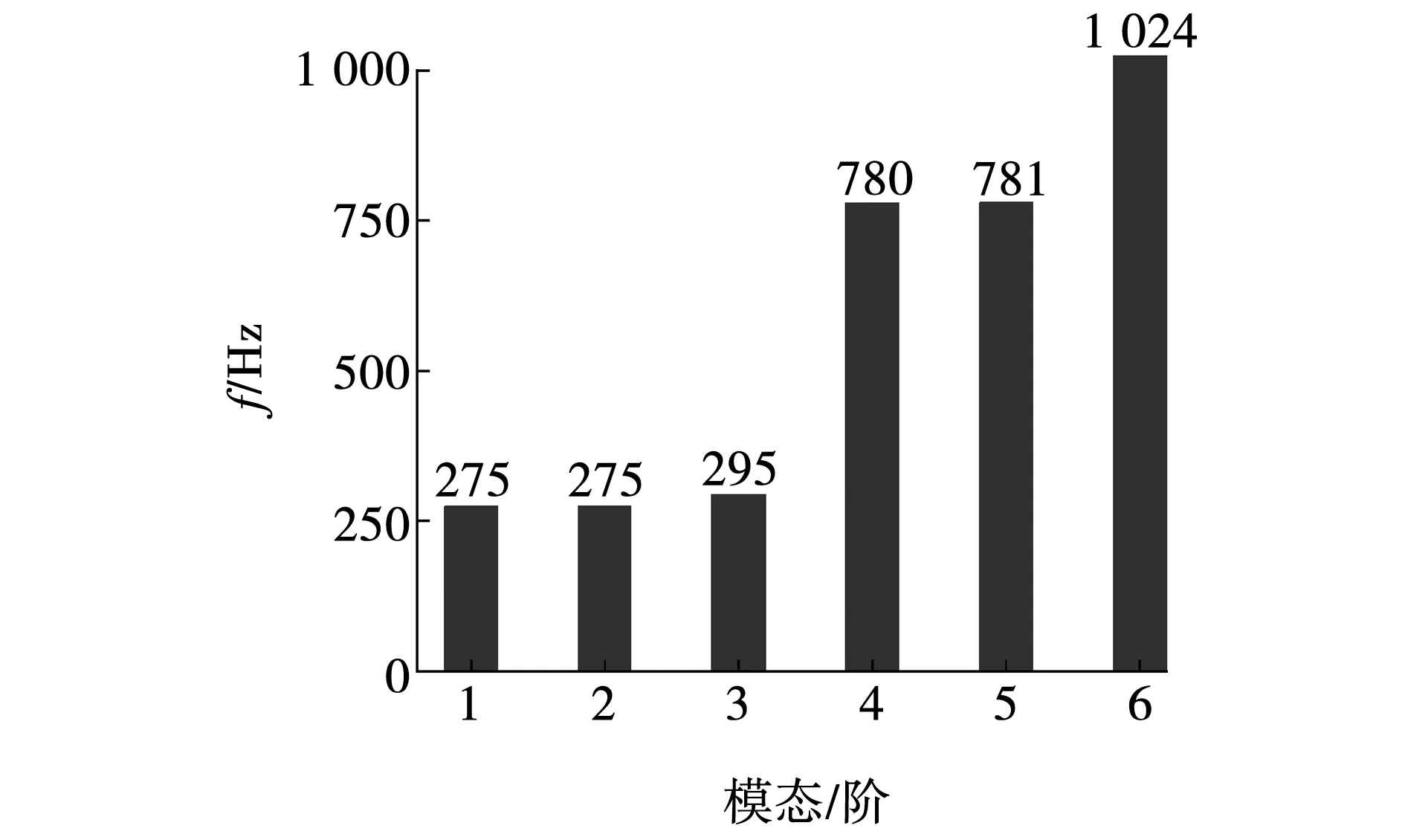
图8 磁辊结构固有频率Fig. 8 Natural frequency of magnetic roller structure

磁辊结构前3阶固有频率十分接近，若涡电流电磁力波径向分量基频高于磁辊结构的1阶固有频率，可能导致磁辊发生共振。前6阶固有频率对应振型如图9所示。以磁辊与有色金属之间的涡流力作为外部激励，1、2、4、5阶振型均为径向弯曲，与磁辊受到外部激励(径向涡电流电磁力波)为同平面；3阶及6阶振动为轴向振动，与磁辊受到涡电流电磁力波不共面，因此，应避免涡电流电磁力波频率高于1、2、4、5阶固有频率。

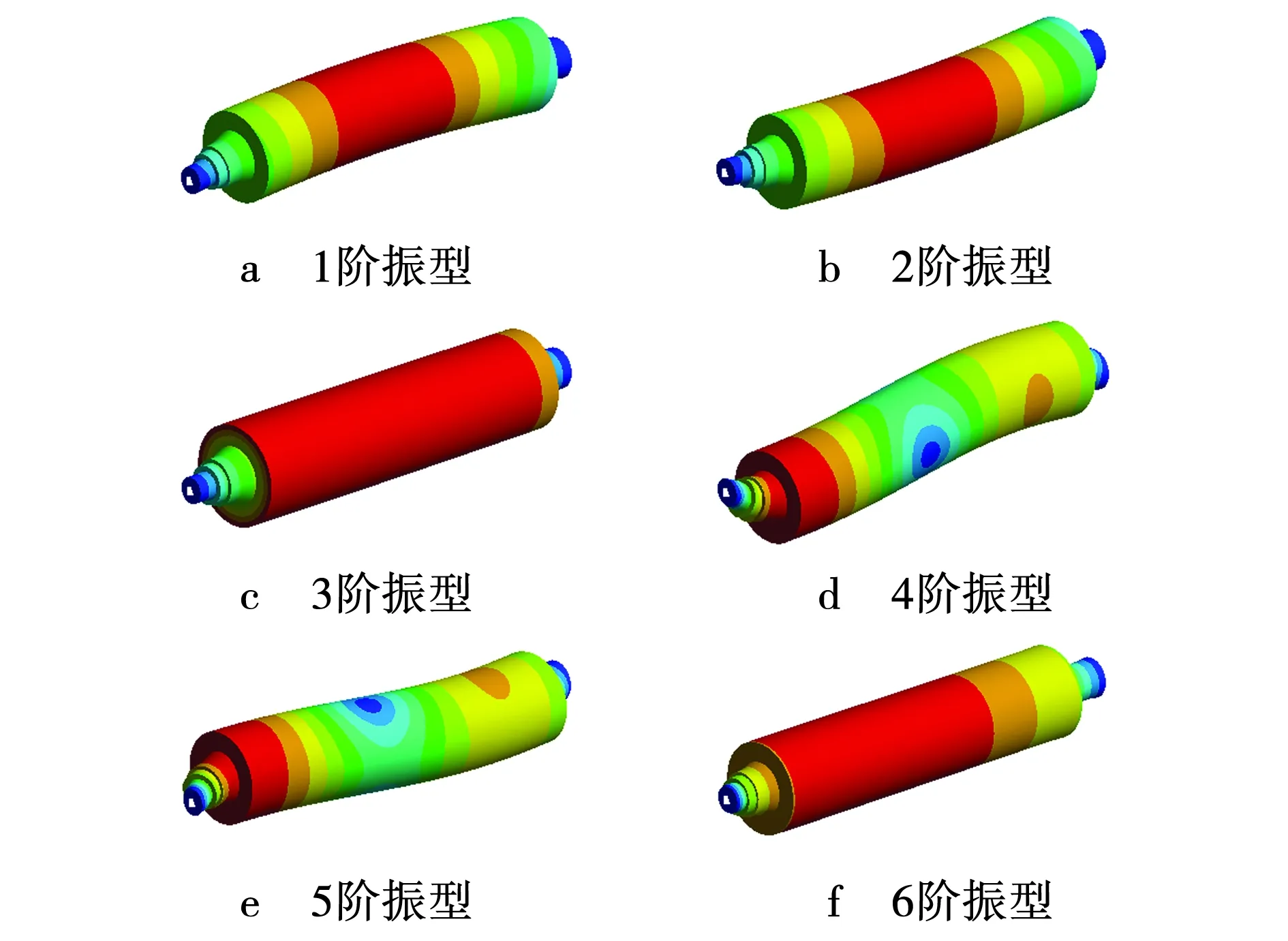
图9 磁辊结构振型Fig. 9 Vibration modality of magnetic roller structure

4 涡电流电磁力波频率

有关涡电流分选机磁感应强度的模拟，Rem在文献[16]中做了十分详尽的研究。结合文献[16]及有限元计算磁感应强度结果，Halbach阵列磁辊的外磁感应强度与传统径向磁化的磁辊外磁感应强度均可以由多个奇数次正弦相量叠加得到，因此，Halbach阵列磁辊产生磁感应强度的径向分量可以表示为

(11)

式中：An——Halbach磁辊外磁感应强度n次波形的幅值；

ωm——磁辊旋转角速度；

k——磁极对数；

n——非负整数，2n+1为磁辊周围磁感应强度谐波阶数[16]。

由于高次谐波幅值过小，仅考虑基波与3次谐波分量，即n=0, 1。

磁感应强度基波为

(12)

阮菊俊[14]推导了涡电流分选机分选有色金属的涡电流电磁力计算方法，涡电流分选机磁辊对矩形有色金属涡电流电磁力为

(13)

式中：γ——有色金属的电导率；

v——传送带传输速度；

Sp——垂直于磁辊磁感应强度径向分量方向的横截面积；

α——分离角度；

δT——有色金属形状参数。

决定涡电流电磁力频率的因素仅为磁辊外磁感应强度径向分量Br及磁辊表面磁感应强度Bm[14]，而Bm与Br同频，设Bm的幅值为Br的u倍，其余与频率无关的系数写为K，则涡电流电磁力波为

(14)

磁辊外磁感应强度径向分量

Br=A1sin[k(α-ωmt)]+A3sin[3k(α-ωmt)]。

(15)

将式(15)代入式(14)，涡电流电磁力波为

2uKA1A3sin[k(α-ωmt)]sin[3k(α-ωmt)]+

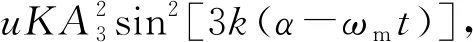
(16)

计算得

uKA1A3[cos[2k(α-ωmt)]-cos[4k(α-ωmt)]]+

(17)

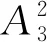
磁感应强度5次谐波最大仅为基波的7%，故可将THD视为3次谐波相对基波大小百分比。

5.1 共振因素分析

涡电流分选机运行时，磁辊结构高速旋转，有色金属受到涡电流电磁力同时反作用于磁辊结构，当其频率高于磁辊固有频率时，磁辊会产生共振[9]。

求解固有频率为共振因素分析的基础，由式(9)及式(10)可知，磁辊结构的固有频率仅与其自身质量、刚度有关，与外部结构无关。由式(13)可知，有色金属的电导率、磁导率、形状等因素仅影响涡电流电磁力的幅值大小，与其频率无关。当涡电流电磁力的垂直分量高于有色金属自身重力时，有色金属被抛出。因此，涡电流电磁力频率高于磁辊固有频率的条件下，混合物料中有色金属的质量增加导致磁辊的振动幅度增大，但仍与涡电流电磁力频率无关。

5.2 共振校验

针对有限元计算求得磁辊结构外磁感应强度频率及对涡电流电磁力波频率的推导与分析结果，定义第i次谐波产生涡电流力与基波幅值比为Ni，文中研究非均匀Halbach阵列磁辊对有色金属的径向涡电流电磁力波频率分析计算结果如表3所示。

由表3可知，随着磁辊的等效磁极角度增加，涡电流电磁力基波频率逐渐降低。Halbach阵列主磁极占比M取0.5时，涡电流电磁力波无谐波。磁极数p为24极时，磁辊产生涡电流电磁力基波频率f1为320 Hz，高于磁辊1阶固有频率275 Hz，易导致磁辊结构共振。

等效磁极数p为12、16极时，磁辊产生涡电流电磁力基波频率f1为160、212 Hz，均低于磁辊各阶固有频率，2次及3次谐波频率均高于磁辊结构1阶固有频率。当M取0.4～0.6时，2次谐波幅值较小，其他比例磁辊产生涡电流电磁力的2次谐波幅值最大值超过基波分量幅值，易导致磁辊结构共振，因此，应避免主磁极占比M超出0.4～0.6范围。

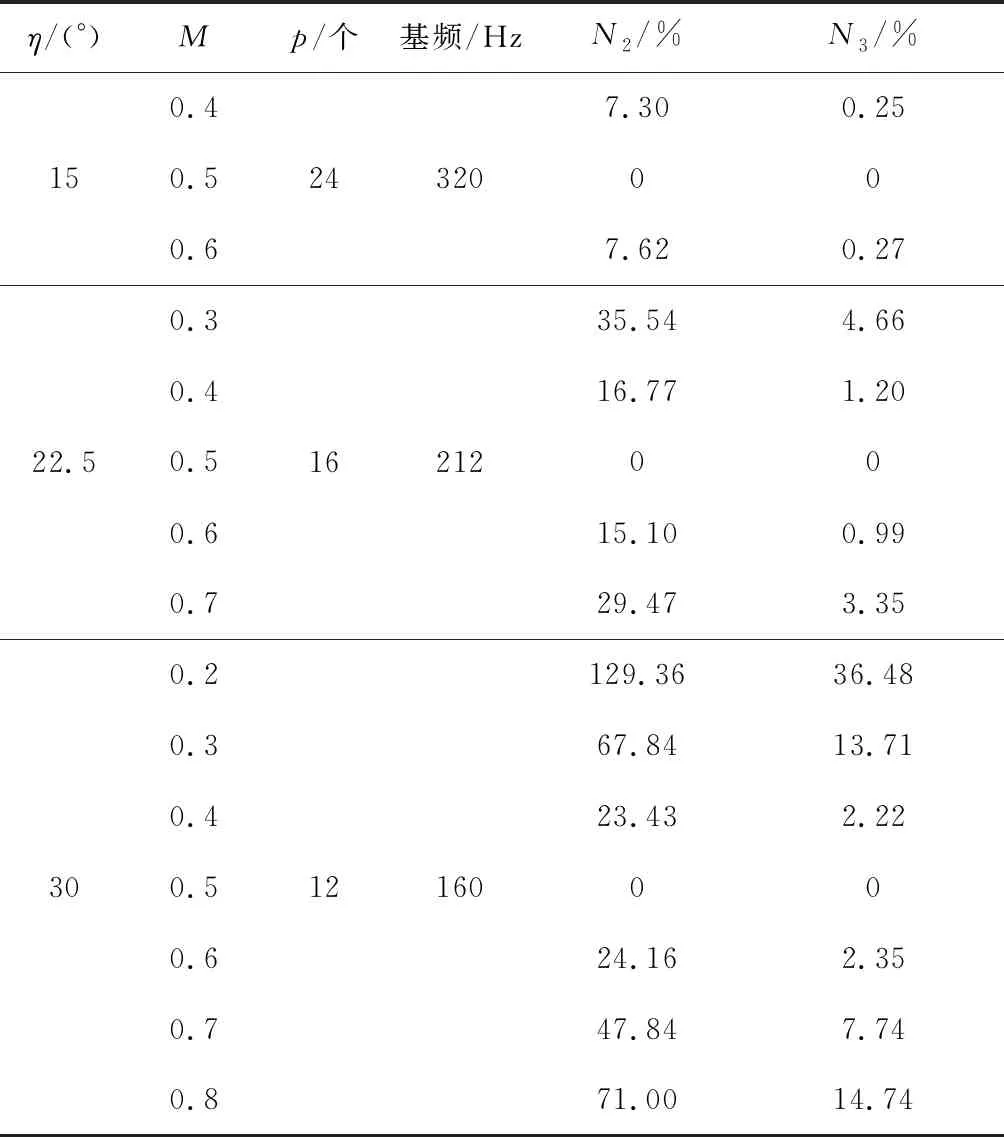
表3 径向涡电流电磁力波计算结果

随着主磁极角度占比M逐渐增大或减小，涡电流电磁力波的2次及3次谐波幅值随之增大。为避免磁辊结构共振，采纳Halbach阵列的有色金属涡电流分选机磁辊设计为非均匀磁极时，主磁极占整个磁极的最佳比例为0.4～0.6，可以有效削弱磁辊结构共振。

6 结 论

为避免涡电流分选机运行过程中磁辊发生共振，磁辊结构的模态分析具有非常重要的意义，文中采用有限元方法得出了磁辊结构的前6阶固有频率，推导并计算了磁辊结构与有色金属之间的径向涡电流电磁力波频率，得出了避免磁辊共振的主磁极角度占等效磁极比例的范围。所得结论可以有效避免涡电流分选机运行过程中，非均匀Halbach阵列磁辊结构产生共振。

(1)研究磁辊结构的前6阶固有频率在275～1 024 Hz之间，且1阶固有频率与2阶固有频率相等，前6阶振型为径向弯曲或轴向振动。

(2)当主磁极与辅助磁极角度相等时，磁辊外磁感应强度径向分量及切向分量谐波含量极少。磁极结构非均匀时，磁辊外磁感应强度径向分量含有3次谐波，主磁极占比M增大或减小时，3次谐波幅值均会增加。

(3)涡电流分选机磁辊与有色金属之间涡电流电磁力波基波频率为磁辊外磁感应强度径向分量基波频率的二倍，且含有偶数次谐波，其谐波幅值变化趋势与磁辊变化趋势保持一致。涡电流分选机磁辊设计为非均匀Halbach阵列时，主磁极占比M为0.4～0.6时，磁辊结构不易发生共振。