基于改进帧间差分的动态目标检测算法

杨庆江， 冯新宇， 李钊枢， 孙向瑞， 林宪峰， 王金旭

(1.黑龙江科技大学 电子与信息工程学院， 哈尔滨 150022； 2.国网黑龙江省电力有限公司黑河供电公司，黑龙江 黑河 164300； 3.黑龙江帕瓦节能环保科技有限公司， 哈尔滨 150001)

0 引 言

随着智能监视系统的飞速发展，视觉处理技术已经日益深入到人们的日常生活。目前，动态目标检测已成为视觉处理的重点研究方向，广泛应用于安防、体育和交通等领域。动态目标检测是指在各种目标运动场景中，通过检测算法选定当前区域的动态目标，利用该目标的坐标、轮廓等信息，分析当前场景中动态目标的相关数据，将检测信息以视觉图像的方式展现。检测的重点在不丢失目标情况下持续对目标进行检测和追踪[1]。在实际的视频监视系统中，需要其能够实时地检测目标，因此，如何提高检测目标的实时性、准确性是学者们一直关注的重点。

在提取运动信息时，常会出现动态目标内部像素点缺失，即“空洞”现象，以及目标边缘断裂等问题，直接影响目标检测的准确性。郭治成等[2]提出了一种基于自适应复杂背景的建模方法，降低了复杂场景下提取前景目标的难度。刘宏飞等[3]利用卡尔曼滤波和匈牙利匹配算法的融合，实现运动目标连续跟踪。都雪静等[4]提出一种结合光流法和背景建模的车道识别算法，对图像进行自适应的ROI分割，有效提高了车道线识别的效果和效率。陈媛等[5]给出一种基于最大模糊熵阈值选取的检测算法，弥补了传统三帧差分法检测运动目标出现内部“空洞”，轮廓不连续等不足，提高了算法的检测性能。温杰[6]利用中值滤波代替高斯滤波，采用Sobel算子实现梯度值的计算，将动态目标的边缘信息近乎完整提取，提高了算法的精确度。综上，对于动态目标检测算法性能的提升，有学者采用传统的光流法、背景差分法、帧间差分法，笔者采用融合Sobel的四帧差分法，同时解决“空洞”和边缘断裂等问题，提高动态目标检测的准确率。

1 动态目标检测算法

1.1 帧间差分算法

传统的目标检测算法常用帧间帧差法作为运动信息提取的算法，其计算和实现流程简单，适应光线变化和动态背景的能力强，但其对动态目标信息的提取有限，无法避免提取过程中出现的“空洞”、轮廓不完整，很难将完整的目标信息提供给后续的图像处理[7]。为避免该情况的发生，同时又保证算法的优点，提出了四帧差分算法提取动态目标。

图像采集设备采集的视频流数据具有连续的特点，若连续的帧数之间，采集图像像素点未有明显变化，说明当前环境内没有运动目标。如果连续的图像像素点有明显的数据变化，则变化像素点即为运动目标，帧间差分法就是应用了上述思想。该算法仅仅使用两帧数据进行帧差，得到差分数据后，从而提取运动目标，二帧差分算法提取运动目标流程见图1。

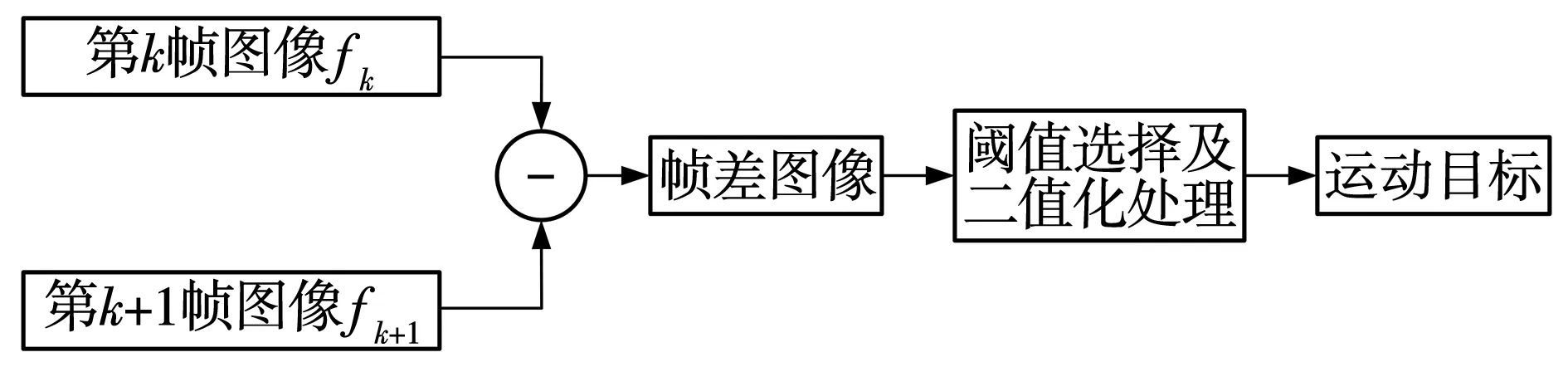
图1 二帧差分算法流程Fig. 1 Inter-frame difference algorithm flow

由图1可见，其流程主要分为帧差和二值提取，二值化需要预先设置二值化所需阈值T，而环境的变换会影响T的取值，文中采用了自适应阈值的二值提取，来适应不同的环境。假设视频图像序列中任意连续的两帧图像，两帧间差分为

Dk(x,y)=|fk(x,y)-fk+1(x,y)|。

(1)

由式(1)中fk(x,y)可知，视频流中相同像素点的部分为静止背景，在差分运算中已经消除，余留像素点即为动态目标部分像素点，即需要提取的像素数据。经式(1)差分图像Dk(x,y)二值化处理，得到差分结果二值图像为

(2)

式中，T——二值化自适应阈值。

在此基础上，通过不断叠加差分运算，检测运动目标，四帧差分运算的流程如图2所示。

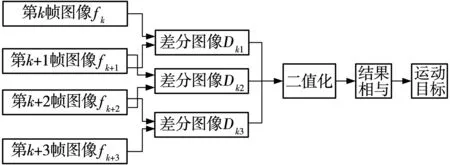
图2 四帧差分流程Fig. 2 Four-frame differential flow

四帧差分算法具有足够多的帧图像数据，避免了差分得到的目标轮廓不完整，其流程在上一算法的基础上加入了多帧二值结果相与的步骤，设fk、fk+1、fk+2、fk+3为视频流中连续四帧图像数据，通过两两差分运算，提取Dk1、Dk2、Dk33组差分图像数据，选定阈值T二值化后，将所有结果与运算，即可获取更为清晰的动态目标轮廓信息。关于四帧差分运算的运算逻辑，如式(3)～(6)所示，Rk1、Rk2、Rk3为二值化处理后的图像数据。

(3)

(4)

(5)

(6)

该方式可以更为完整提取动态目标的轮廓信息，提高目标检测的精度，降低误检率。

1.2 Sobel边缘检测算法

由于传统目标检测算法在提取运动目标时，易出现目标边缘割裂的问题，降低检测精度。引入Sobel边缘检测算法，使目标轮廓信息更为清晰、完整，降低检测运动目标的难度，提升检测的精确度。Sobel、Roberts、Prewitt作为经典边缘检测算子，其中，Roberts算子运算速度非常快，定位精度高，在水平和垂直方向效果好，但是对噪声敏感[8]，抗干扰能力相对较弱，因此，适应能力很低。Prewitt和Sobel算子均是由3×3矩阵卷积，其抗噪声能力和滤波能力较Roberts算子有较大提升，由于Prewitt算子在权值计算时未有差异性，所以相对于Sobel算子，其边缘效果不够准确，且轮廓较大，会影响后续实验效果。Sobel算子具有更高的灵活性，可以区分像素点距离进行不同计算，因此，文中选用Sobel边缘检测算子来提取运动目标轮廓信息，以方便后续处理。

Sobel算子是通过卷积实现，也就是对传输过来的图像像素值进行求梯度运算，其实现原理见图3。

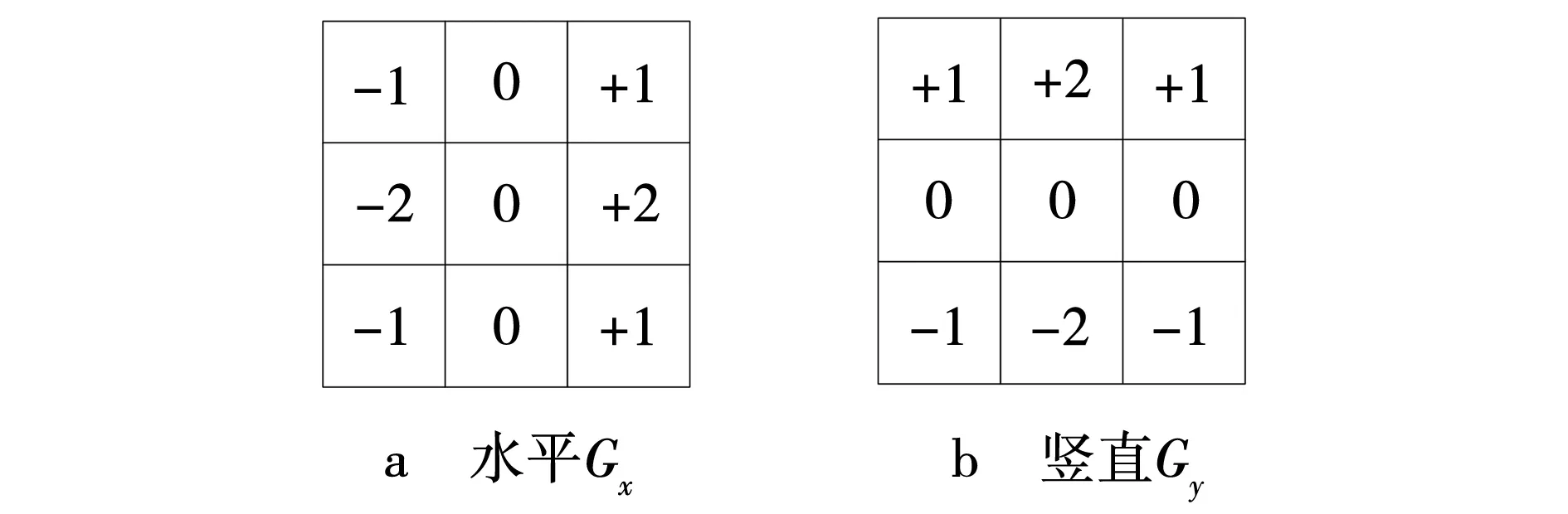
图3 卷积矩阵实现原理Fig. 3 Principle of convolution matrix implementation

由图3可知，该算法需要对图像数据的两个方向进行矩阵卷积，分别为水平Gx和竖直Gy。将两矩阵与图像像素点数据做卷积运算，即可分别得出水平和竖直的图像灰度值。Sobel卷积矩阵为

(7)

(8)

式中，M——图像数据。

将卷积得到水平、竖直方向灰度值通过式(9)计算该点的边缘灰度值为

(9)

为提高算法的运算效率，减轻系统实现难度，可以将GR(x,y)计算公式简化为

GR(x,y)=|Gx|+|Gy|。

(10)

根据室内环境设定好边缘检测阈值后，将设定的阈值与式(10)像素点梯度值GR(x,y)进行对比。若阈值小于该点的值，该像素点为图像的边缘，否则为图像的内部信息或者背景。

1.3 融合Sobel的四帧差分法

文中在四帧差分算法的基础上，通过Sobel边缘检测算子与四帧差分运算相结合的目标检测方式，减少该问题的发生概率，使动态目标轮廓信息更为完整并以此作为后续动态目标提取的准备阶段，提升动态目标检测的精确度。该方法分别对原视频序列中的图像进行四帧差分运算和Sobel边缘检测运算，随后采用形态学滤波等手段处理图像数据检测运动目标，算法流程如图4所示。

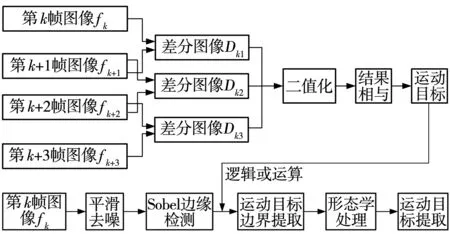
图4 融合Sobel边缘检测的四帧差分法流程Fig. 4 Flow of four-frame difference method

由图4可见，根据1.1节图2四帧差分检测流程，对原来序列的第k帧fk(x,y)、第k+1帧fk+1(x,y)、第k+2帧fk+2(x,y)、第k+3帧fk+3(x,y)进行两两差分运算，分别得到差分图像Dk1、Dk2、Dk3。分别对差分结果Dk1、Dk2、Dk3二值化处理。二值结果相与，获取最终目标二值像素。使用Sobel算子对采集图像的第k帧fk(x,y)进行边缘化处理。二值化图像和边缘图像逻辑或运算提取目标完整轮廓。形态学处理无用像素点，完成动态目标的提取。

2 实验与结果分析

2.1 检测效果

利用Matlab实现对图像序列的处理，实验采用的PC机配置CPU为Intel Core i5-9300h，2.4 GHz，GPU为GTX1660ti，内存为16 G。应用的环境为室内环境，主要采集人的运动数据，由于人正常步行速度约为1.1 m/s，所以检测的目标是在低速环境下，监视视频是由校园监控所提供，选取视频流中连续帧的图像，在Matlab仿真环境中，设置合适的环境阈值T，对算法进行仿真实验，原视频序列连续四帧图像如图5所示，差分结果如图6所示。

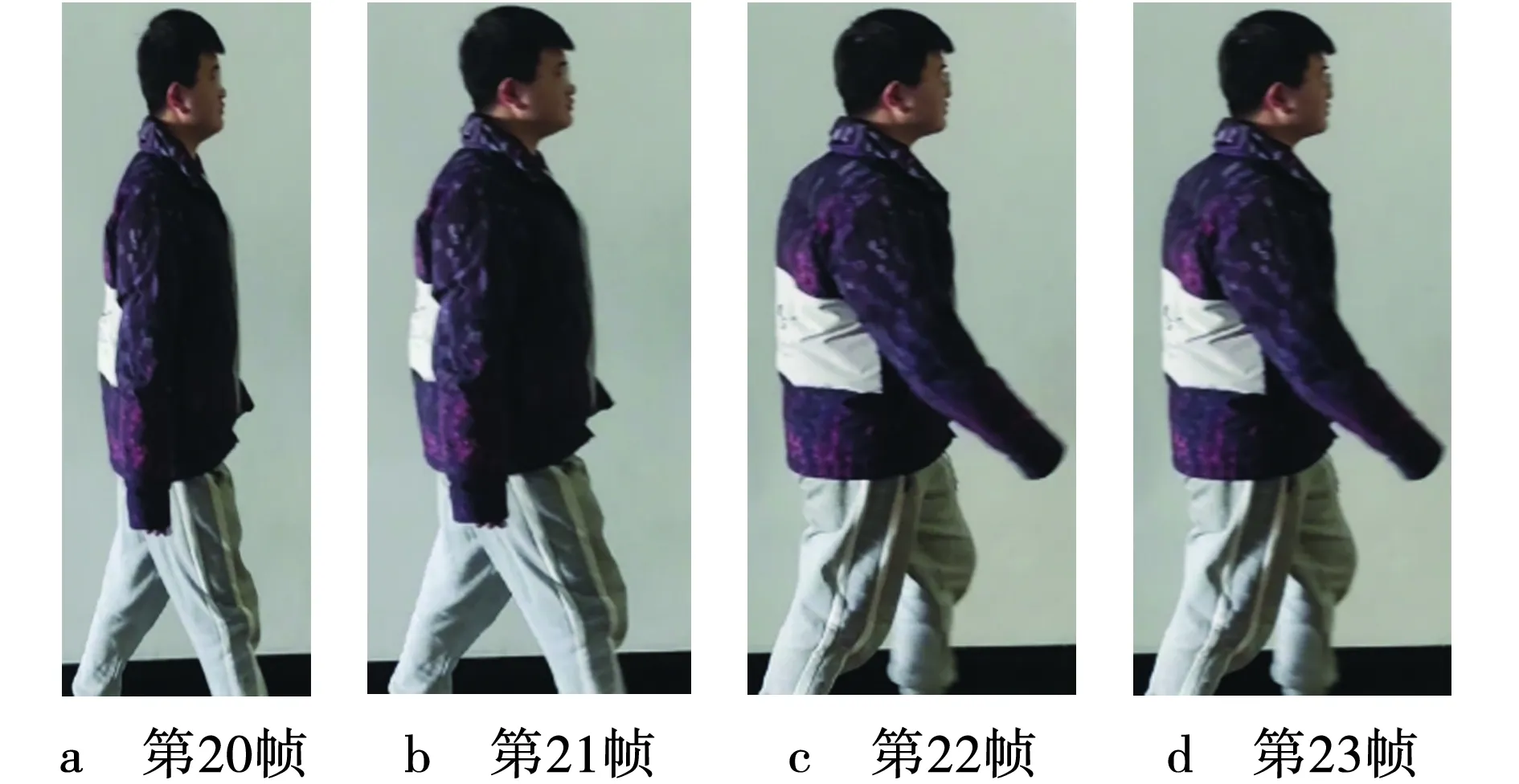
图5 原视频序列Fig. 5 Original video sequence

由图6可见，二帧差分算法提取轮廓信息的完整度约20%，目标轮廓大面积缺失，背部图像信息无法提取。若该方法作为目标检测算法提取动态目标，无法保证检测的精确度，而且算法容易受到目标速度影响，运动速度过快，二帧运动目标不连续，会导致“空洞”。三帧差分算法检测同一运动目标的轮廓信息与二帧差分算法相比，上涨了一倍左右，检测信息完整度达到40%，目标背后轮廓仍有大面积缺失。虽然相较于二帧差分算法已经有了明显的提升，但大面积空洞和不完整的轮廓只能给后续目标的检测增加难度。四帧差分算法轮廓信息达到了65%，目标轮廓更为明显、清晰，有效降低了空洞现象，能够检测到目标近乎完全的轮廓信息，但后背轮廓还是有一定的割裂，继续叠加帧差运算，如表1所示。其中，运算速度为v；误检率为α；轮廓完整信息为β。

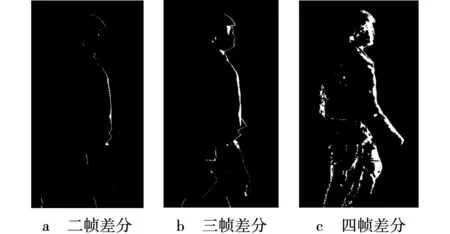
图6 Matlab差分结果Fig. 6 Matlab differential result graph

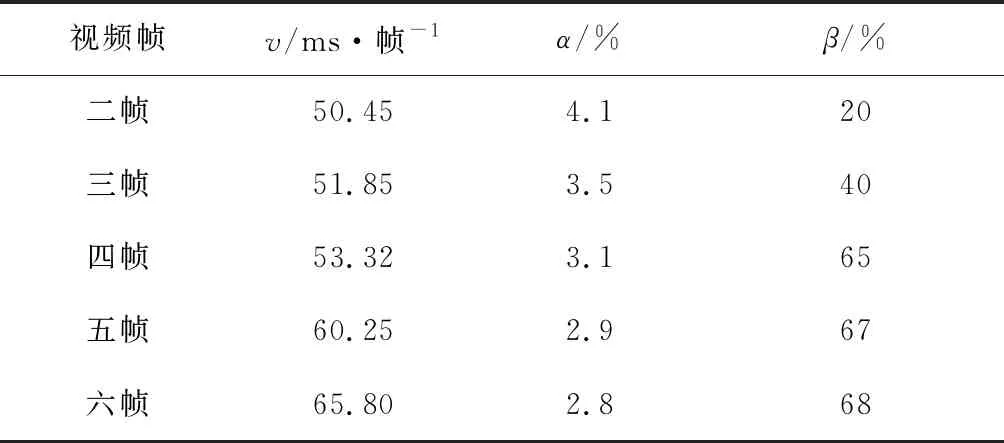
表1 帧间差分法仿真结果对比

由表1可知，在相同室内环境下，二帧到三帧的处理方式提升幅度几乎一倍，三帧到四帧约提升60%；但四帧差分继续向上叠加提升幅度大幅降低，仅为1%左右且运算速度明显减慢，误检率有一定下降，说明算法对无用二值像素点的滤除有一定作用，文中最终选择对四帧差分算法进一步优化。

采用文中提出的融合Sobel边缘检测的四帧差分算法进行仿真实验，Matlab仿真结果如图7所示。图7a为四帧差分检测的结果。四帧差分提取的运动目标存在模糊不完整边缘，会产生“空洞”现象。图7b为Sobel边缘图像。由图7b可以看出，检测边缘信息较为完整，但边缘像素点不连续。图7c为融合了Sobel边缘检测的四帧差分算法。由图7c仿真结果显示，运动目标信息达到了80%以上，“空洞”和边缘不完整问题得到极大的抑制，目标边缘连续完整，继承了两种算法对目标提取的优点，使动态目标像素信息更为完整。

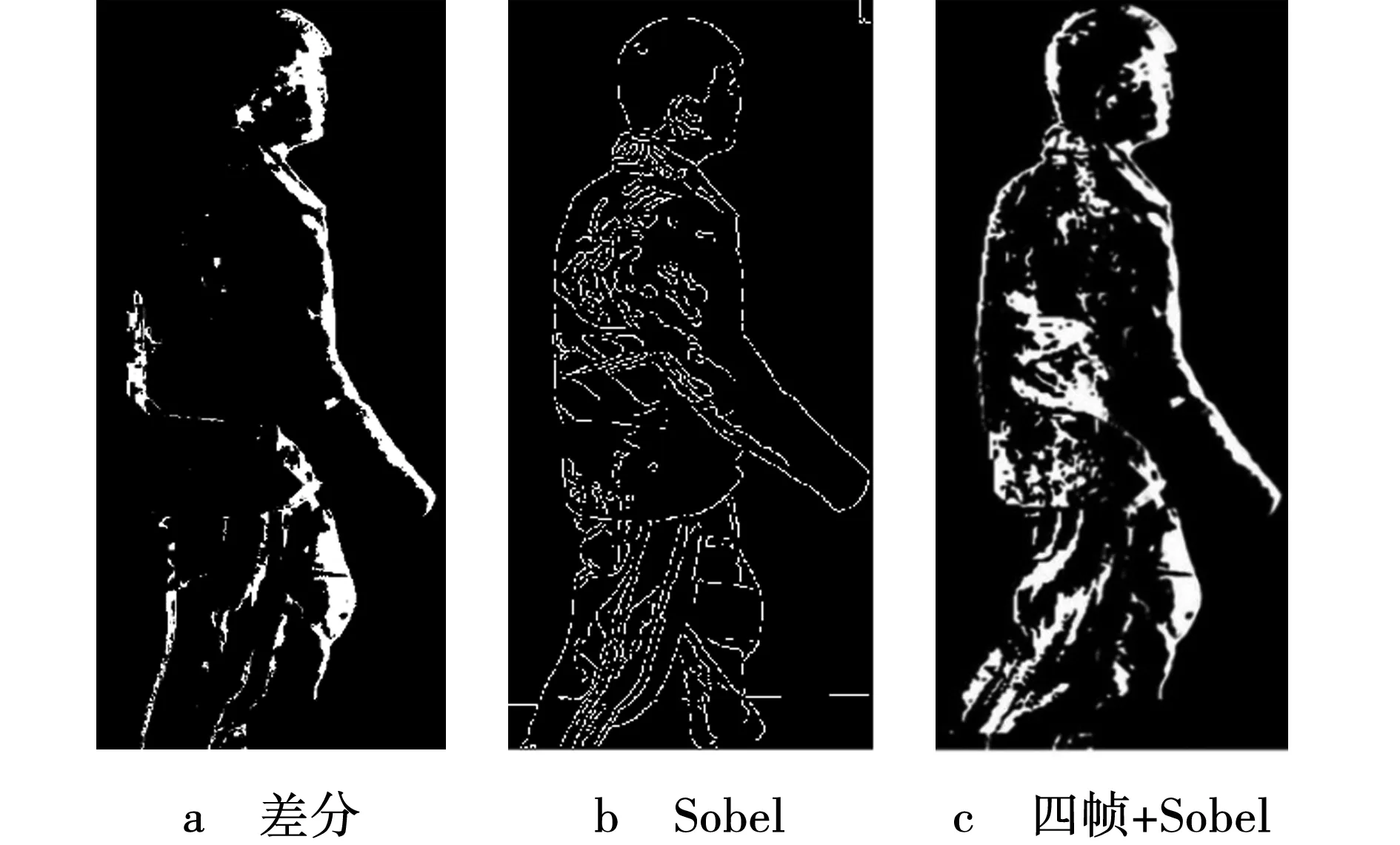
图7 Matlab仿真结果Fig. 7 Matlab simulation results

2.2 检测精度

采用Matlab中的boundingbox函数，使用最小包围框框选上一节算法提取出的运动像素点，实现对运动目标的检测，可以得到在相同环境，相同阈值下运动目标区域，图8a、b为四帧差分检测结果，图8c为融合了Sobel的四帧差分法检测结果。通过仿真对比，采用四帧差分算法的最小包围框对于动态目标的检测存在大量的不准确帧，融合了Sobel的四帧差分算法可以更准确的检测运动目标。

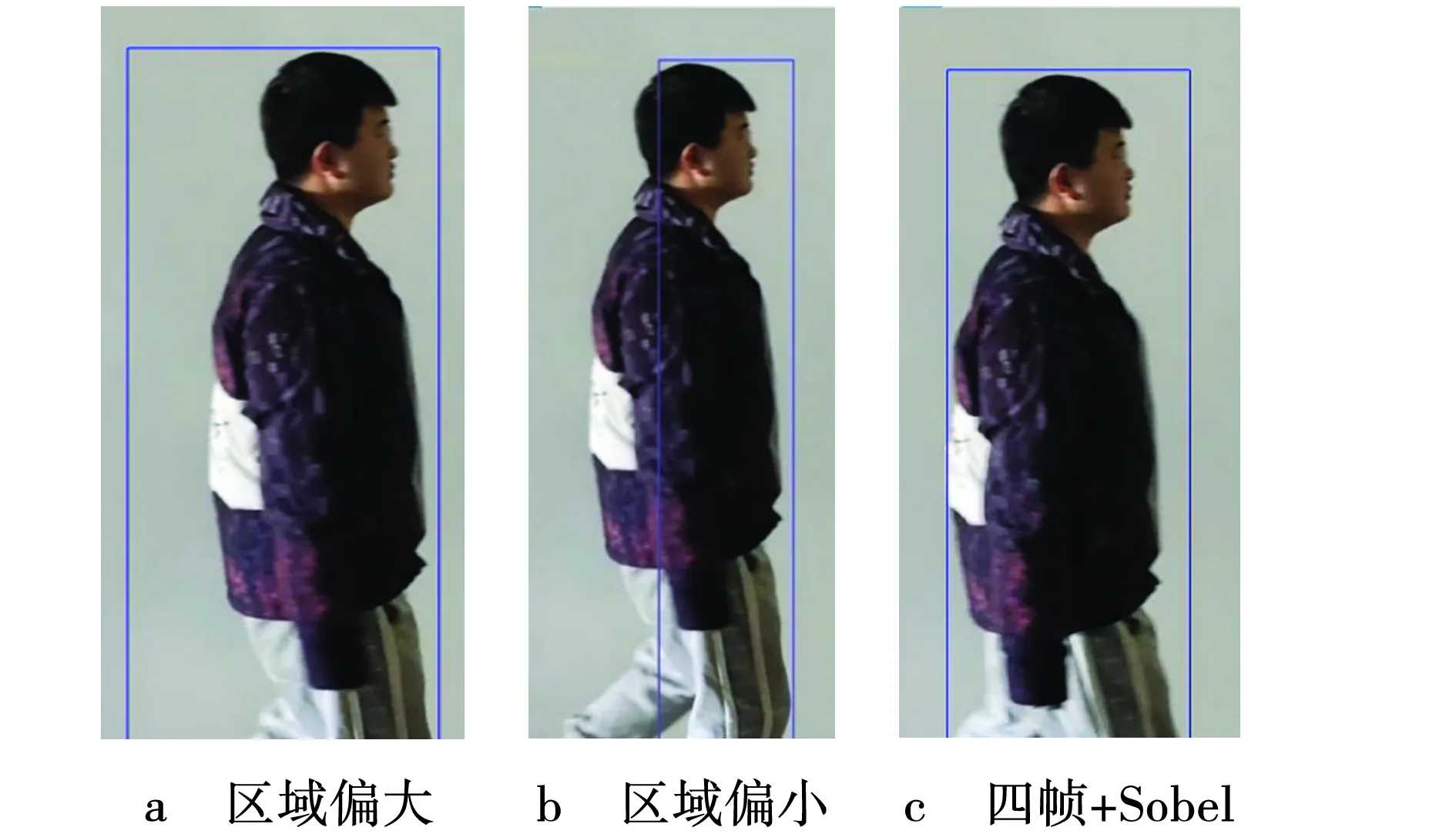
图8 目标检测与检测仿真实验Fig. 8 Target detection and detection and tracking simulation experiment

为了进一步验证改进算法的有效性，从室内监控中获取不同时段的监控录像，在Matlab环境下采用相同的方式实验150次，统计其检测准确率η、误检率ζ，综合指标H见表2。检测准确率η表征正确检测动态目标帧数占总动态目标帧数的比例；误检率ζ表征错误检测动态目标帧数占总检测帧数比例。

表2 算法检测对比

式中：AP——正确检测动态目标的帧数；

BP——检测出非动态目标的帧数；

FN——未检测出动态目标的帧数。

文中引入一个综合指标H来评估检测算法的整体性，如果检测准确率越高和误检率越低，则H值就越大，算法性能越高[9]，H值定义为

由表2衡量标准对比显示，改进算法相对于普通四帧差分更准确，误检率更低，H值提升约18.6%，算法性能更为优秀。

3 结 论

(1)针对二帧差分算法提取动态目标轮廓、边缘信息不完整和“空洞”现象，提出了融合Sobel的四帧差分法，在二帧差分的基础上，叠加帧差运算，采用自适应四帧差分使检测的运动目标信息达到了65%，改善了“空洞”问题。

(2)由于目标轮廓还存在大量边缘不连续，引入Sobel算子增强边缘轮廓，将目标信息完整度提升到80%，综合评估H值提升18.6%，有效提高了动态目标检测的准确性。文中研究内容在监视系统上有一定的应用价值，可向多目标检测继续提升。