基于DDSRF-PLL的并网逆变器复矢量导纳分析

苏勋文， 王浠再， 姜泽浩， 查鹏飞

(黑龙江科技大学 电气与控制工程学院， 哈尔滨 150022)

0 引 言

直驱风机并网主要依靠电力电子变换器，对于并网变换器的稳定性研究尤为必要。在弱交流系统中，风电机组控制器与电网之间易引发次同步振荡，被称为次同步相互作用[1-2]。同时，由于逆变器控制结构是不对称的，所以并网点的电压、电流会出现频率耦合现象，进一步导致系统失稳[3-4]。目前，对并网逆变器研究分析方法主要为阻抗分析法，在dq旋转坐标系下建立并网逆变器的小信号模型，综合考虑控制器的影响，得到并网逆变器的等效阻抗模型，通过广义奈奎斯特判据判断系统稳定性。研究表明，在不同控制策略下，dq坐标系中并网逆变器的小信号阻抗特性不同。锁相环、电流反馈控制和功率反馈控制对逆变器阻抗都存在影响，在弱电网下，锁相环带宽的变化可能导致逆变器系统不稳定[5-6]。

旋转坐标系下的dq阻抗模型建模方法较为简单，但在面对旋转坐标系下控制器不对称引起的频率耦合时，该方法无法体现频率耦合关系[7]。王国宁等[8]在静止坐标系下建立三相并网逆变器的复变量导纳模型，讨论了自导纳和伴随导纳对逆变器稳定性的影响，根据导纳模型可以给出系统的稳定裕度。邹小明等[9]探究了并网逆变器中频率耦合现象的机理，给出了耦合频率下并网逆变器的导纳模型，对导纳可以直接使用奈奎斯特判据判断稳定性，简化了稳定性判定过程。张学广等[10]分析了锁相环、电压环和电流环多重因素对并网变换器导纳模型的影响，研究了频率耦合机理，针对锁相环和电压环的不对称结构，提出了抑制频率耦合的措施。武相强等[11]通过谐波线性化的方法，分析了DDSRF-PLL的频率特性，给出了LCL逆变器的序阻抗模型，在锁相环中加入超前校正环节，提高逆变器的稳定性。

笔者在静止坐标系下建立并网逆变器的复矢量模型，通过仿真验证导纳模型的正确性，探究逆变器中存在的频率耦合现象机理，利用奈奎斯特判据分析在不同电网强度下导纳模型的稳定性。

1 逆变器复矢量建模

1.1 复矢量表示方法

三相正序、负序电压可以转换到两项静止坐标系下，其表达式的区别为β轴分量的正负号不同。在建模过程中，可以将电网视为理想电网，不考虑电网阻抗，则并网点的电压等于电网电压为

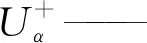
ω0——电压频率;

φ——电压初始相位;

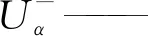
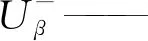
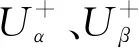
文中所有复矢量形式的变量都以粗体表示，将αβ坐标系中的正、负序电压表示为复矢量形式，代数形式转换指数可形式为

(1)

式中:Uαβ,ω0——αβ坐标下正序电压复矢量；

Uαβ,-ω0——αβ坐标下负序电压复矢量；

ejω0——角速度为ω0的复指数。

由于正、负序电压表达式的差异，两者表达式频率互为相反数，导致其复数表达式互为共轭，如式(1)所示。可以看出，正、负序扰动电压Uαβ,ωp、Uαβ,-ωp差异仅为下角标的负号。据此特点，后文公式中的负序扰动复矢量只需将正序扰动电压的下标角频率增加负号即可。式(1)按照欧拉公式展开，可得对应的复数时域表达式为

1.2 逆变器主电路建模

三相逆变器的主电路结构如图1所示。其中，Udc为直流侧等效电源，Rdc为直流侧等效电阻，Cdc为稳压电容，S1～S6为IGBT开关管，Lf和Rf为滤波电感和寄生电阻，Lg和Rg为电网电感和寄生电阻。

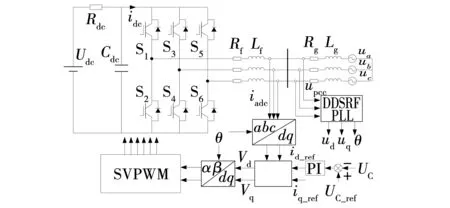
图1 三相并网逆变器系统结构Fig. 1 Structure of grid-tied inverter with feedback control

对逆变器主电路进行小信号建模，可以得到如图2所示的结构，图2中大写字母表示工频稳态分量，小写字母表示扰动分量。如：uα,ωp、uβ,ωp、iα,ωp、iβ,ωp、dα,ωp、dβ,ωp分别表示α、β轴并网点电压、电流和占空比扰动量，Uα,ω0、Uβ,ω0、Iα,ω0、Iβ,ω0、Dα,ω0、Dβ,ω0分别表示α、β轴并网点电压、电流和占空比稳态量，由于直流侧等效为理想直流电源，所以小信号模型中没有直流电源扰动量。

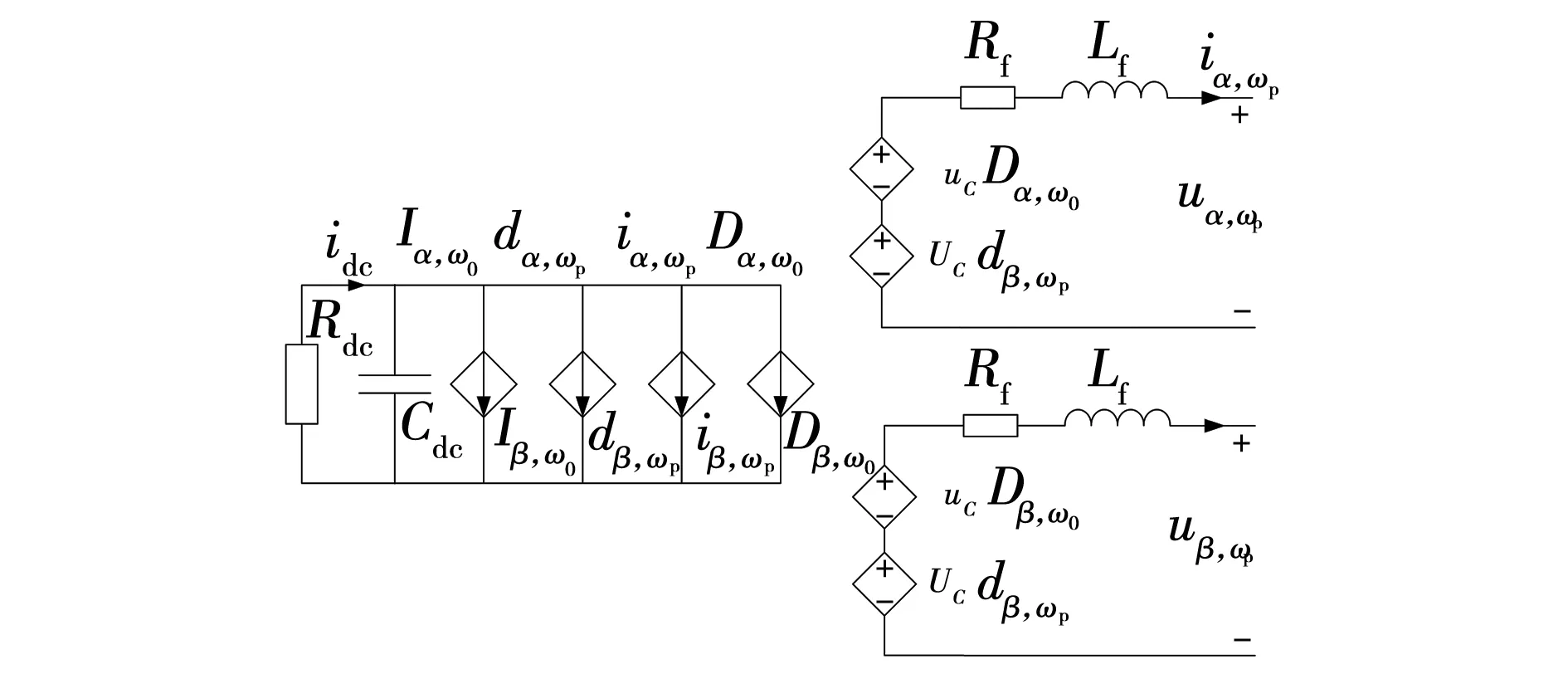
图2 α-β坐标系下逆变器主电路小信号模型Fig. 2 Small-signal circuit model of inverter in α-β frame

根据小信号模型可以建立直流侧和交流侧方程为

Zac(s)iαβ,ωp+uαβ,ωp=UCdαβ,ωp+uCDαβ,ω0，

(2)

Zac(s)=Rg+sLg，

式中:uαβ,ωp——网侧扰动电压复矢量；

iαβ,ωp——网侧扰动电流复矢量；

UC——电容电压稳态量；

uC——电容电压小信号扰动量；

Dαβ,ω0——占空比稳态量复矢量；

Iαβ,ω0——网侧稳态电流复矢量。

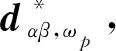
为了简化方程，方便画出控制回路结构图，记

GiuC=Dαβ,ω0UC+Zac(s)Iαβ,ω0，

同时引入控制器输出电压扰动分量和稳态分量为

Vαβ,ωp=UCdαβ,ωp，Vαβ,ω0=UCDαβ,ω0，

此时式(2)可以表示为

1.3 控制回路建模

文中的三相并网逆变器采用双同步解耦锁相环(DDSRF-PLL)跟踪电网相位，通过电压外环和电流内环共同控制逆变器输出，双同步解耦锁相环的结构如图3所示。

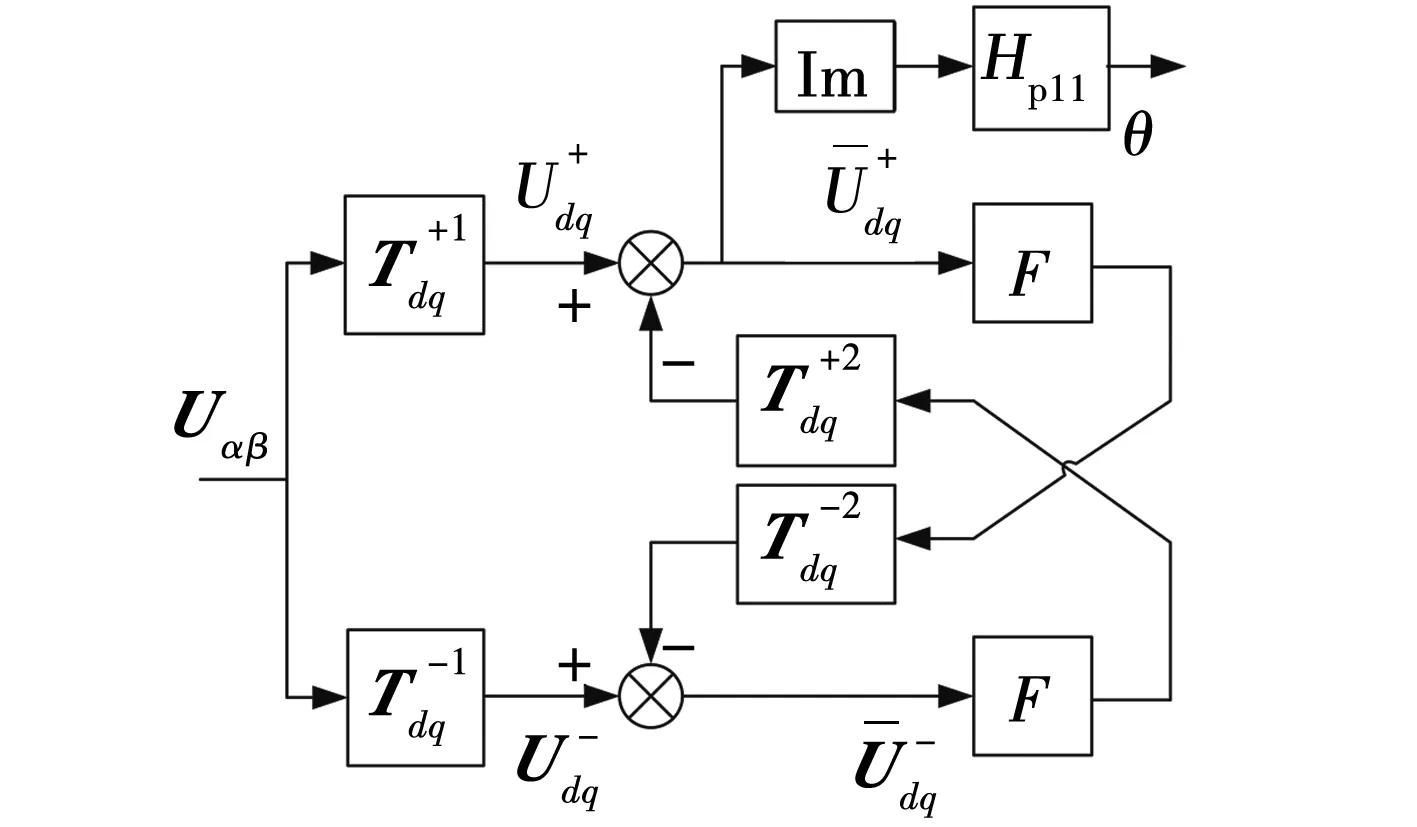
图3 DDSRF-PLL结构Fig. 3 Structure of DDSRF-PLL

由图3可见，Im表示取输入复矢量的虚部，F代表低通滤波环节，Hpll表示锁相环传递函数，其表达式分别为

式中:ωf——滤波器参数；

kpp——锁相环比例系数；

kip——锁相环积分系数。

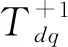
iαβ,ωpe-jω0t=iαβ,ωp-ω0，

根据DDSRF-PLL的结构图，正、负序解耦后的电压表达式为

(3)

(4)

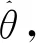
若不考虑PCC点电压dq分量中的稳态值，dq坐标系下的扰动电压量可分为两部分：扰动电压本身和电压稳态分量与相角扰动叠加后形成的扰动量。同理，只要是控制器中进行过派克变换的变量，都会附加一项锁相环干扰分量。SEF-PLL和DDSRF-PLL所产生附加干扰的幅相特性曲线如图4所示。

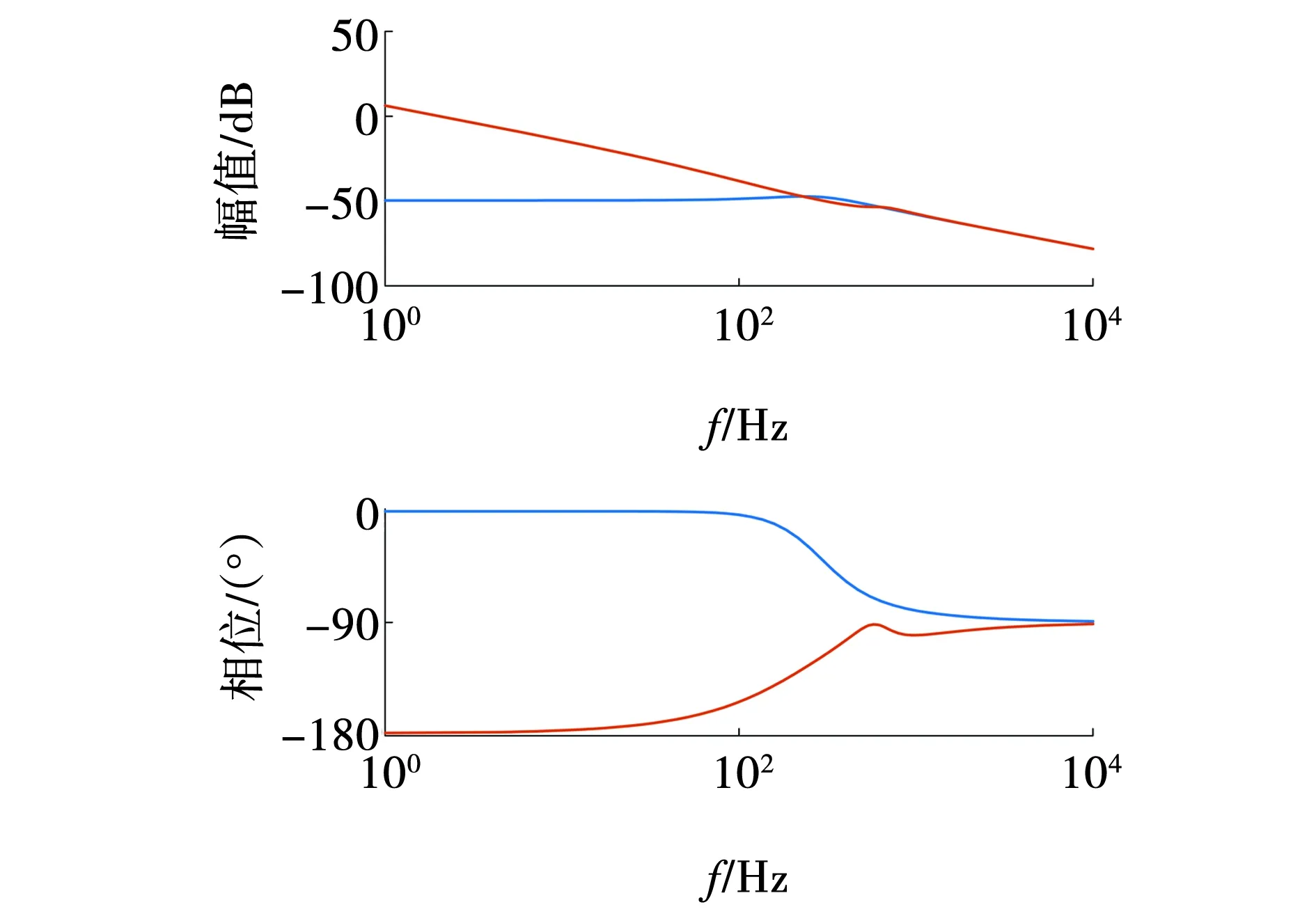
图的伯德图

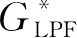
由于复矢量的虚部可以通过共轭作差求得，结合图3中的结构，可列出公式为

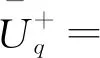
(5)

综合式(4)(5)，可得相角扰动表达式为

(6)

从式(6)可以看出，锁相环的相角扰动包含了扰动电压复矢量的共轭分量，将其转换到静止坐标系中，频率变为2ω0-ωp，此分量也被称作频率耦合分量。并网点电压产生小扰动后，扰动电压经过锁相环会产生频率耦合分量，此耦合电压经过逆变器主电路会进一步产生耦合电流。根据逆变器的控制结构可以画出逆变器控制回路传递函数结构，如图5所示。

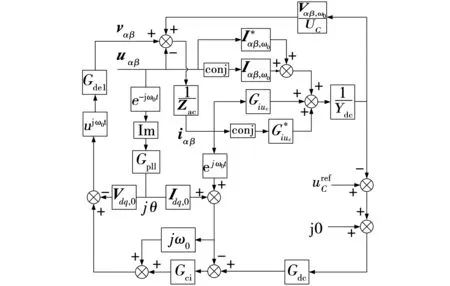
图5 并网逆变器传递函数结构Fig. 5 Block of transfer function on grid-connected converter system

结合主电路和控制回路，可以得到并网点电流与电压的关系式为

G1uαβ,ωp=G2uαβ,2ω0-ωp+G3iαβ,ωp+G4iαβ,2ω0-ωp,

(7)

G4=(Gxi(s-jω0)+Gsub)GiuC，Gaf=Gdel(s)Gpll(s-jω0)，

Gk=(Gci(s-jω0)-jω0Lf)Idq,0+Vdq,0，

GiuC(s-jω0)=Ddq,0UC+Zac(s-jω0)Idq,0，

由于逆变器系统中存在频率为2ω0-ωp的耦合电压，其经过逆变器主电路和控制回路之后，也会产生频率为ωp的耦合电压和电流量，根据文中提到的方法，可以得到与式(7)形式相近的表达式为

G5uαβ,2ω0-ωp=G6uαβ,ωp+G7iαβ,2ω0-ωp+G8iαβ,ωp。

(8)

由于自变量的频率不一样，所以式(7)传递函数中的微分算子s所取频率也会相应变化。

综合式(7)(8)可得：

iαβ,ωp=Y11uαβ,ωp+Y12uαβ,2ω0-ωp，

iαβ,2ω0-ωp=Y21uαβ,ωp+Y22uαβ,2ω0-ωp，

由于经常用到扰动电压、电流的虚部作为控制量，而虚部需由相应共轭量作差求得，相当于正序量和负序量作差，在此过程中，发现正序和负序量之间存在的关系为

(9)

式(9)表明，当求取正序扰动虚部时，将负序量转变为耦合量进行的计算，多出的e2jω0t抵消掉了传递函数中独立的ejω0t，简化了编程计算的难度。

2 导纳模型稳定性分析

2.1 导纳模型频率特性

根据推导出的导纳模型复矢量表达式Y11、Y12、Y21和Y22，绘制出导纳模型的对数幅频特性曲线如图6所示。在图6中使用两种不同颜色分别表示DDSRF-PLL和SEF-PLL的逆变器导纳模型。

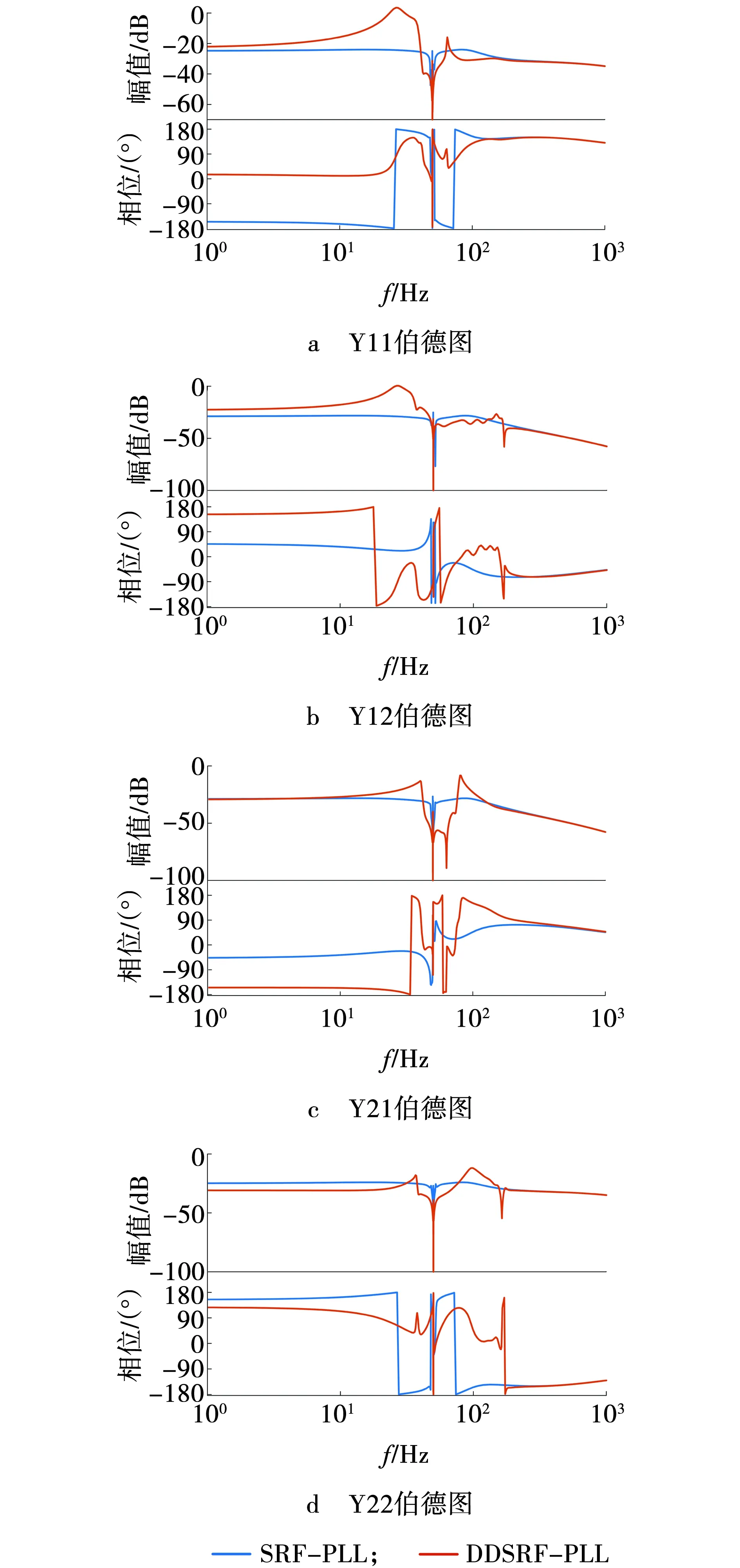
图6 导纳模型伯德图Fig. 6 Bode of admittance model

由图6可知，采用DDSRF-PLL的逆变器在低频段对信号的响应更大，推断逆变器在低频段的频率耦合效应更明显。

2.2 系统稳定性分析

建模过程中，始终将电网看作无穷大理想电网，此时电网内阻为零，因此并网点电压等于电网电压。在进行稳定性分析时，需要考虑逆变器和电网互联系统的稳定性，此时需要考虑电网阻抗，PCC电压不再等于电网电压。将逆变器转化为诺顿等效电路，电网转化为戴维南等效电路，得到如图7所示的电路。

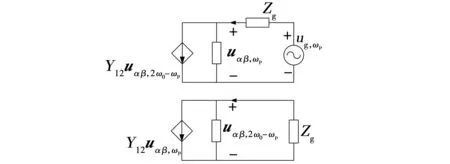
图7 并网逆变器等效电路Fig. 7 Equivalent circuit of three-phase grid-connected inverter

图7中的电网阻抗Zg表达式为

式中:Rg——电网电阻；

Lg——电网电感；

Cg——电网电容。

根据图7并网逆度器等效电路可以求得，电网扰动电压ug,ωp到扰动电流iαβ,ωp的闭环传递函数和并网点电压uαβ,ωp到耦合电流的闭环传递函数。

绘制开环传递函数的奈奎斯特曲线，根据奈奎斯特稳定性判据，即可判定逆变器并网系统的稳定性。开环传递函数为

Gk=ZgYt。

取电网阻抗参数为Lg=7 mH，Rg=0.1 Ω，Cg=8 μF，此时电网短路比为21，画出Gk的Bode图和Nyquist图如图8和9所示。

从图9a可以看出，奈奎斯特曲线包围了(-1，j0)点，图8a中的对数频率特性曲线在32 Hz处穿越-180°线，此时对数幅值大于0，稳定裕度为-1.72 dB，相角裕度为-11.5°，闭环系统不稳定，且在此频率处容易发生振荡。

改变电感值，令Lg=1 mH，其余参数不变，此时短路比为9.2，画出Gk的Bode图和Nyquist图。如图8b、9b所示。从图9b可以看出，奈奎斯特曲线不包围(-1，j0)点，图8b中对数频率特性曲线在32 Hz处穿越-180°线，此时对数幅值小于0，稳定裕度为6.72 dB，相角裕度为20.5°，闭环系统稳定。

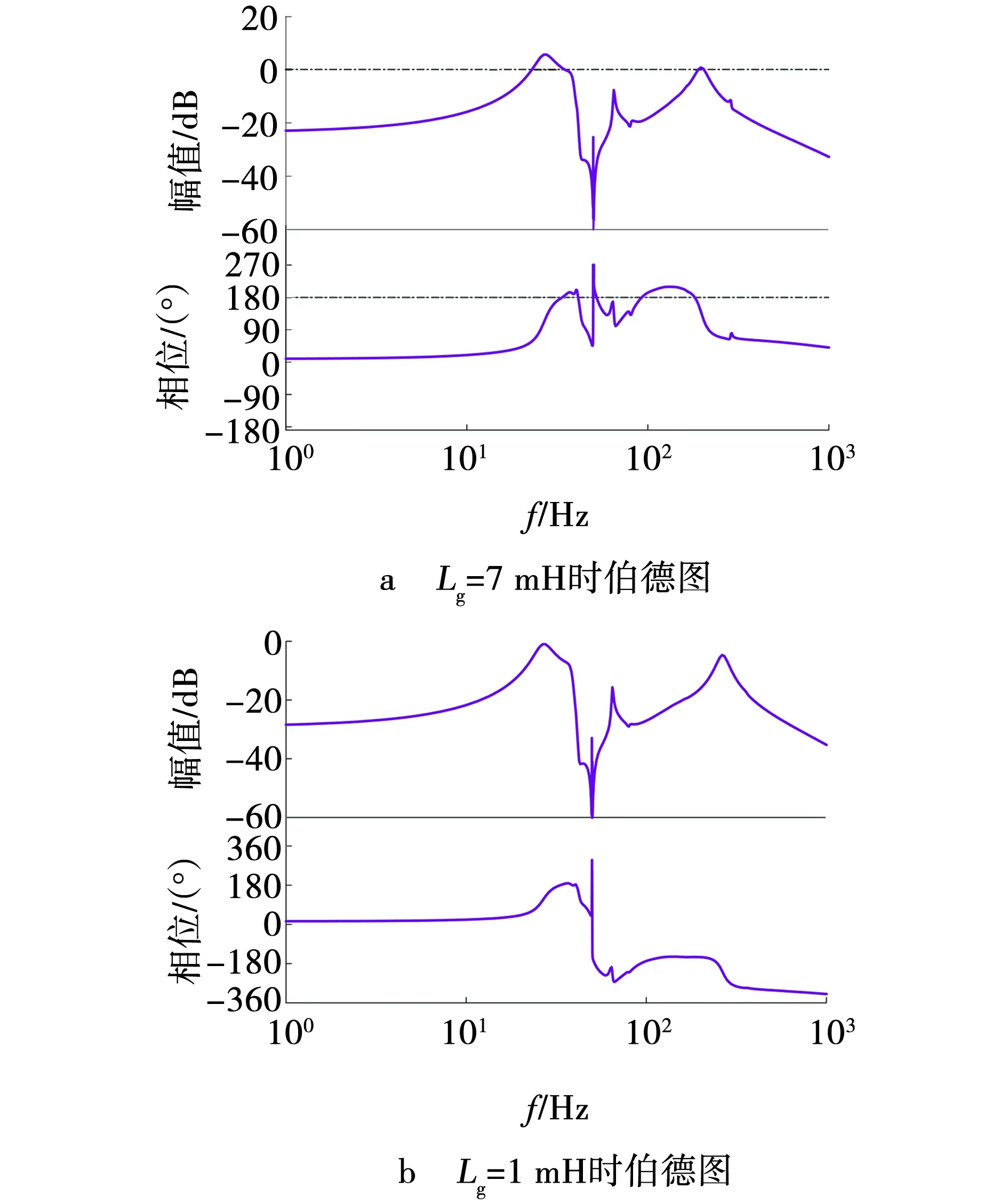
图8 不同Lg值的Gk伯德图Fig. 8 Bode plots of Gk for different Lg

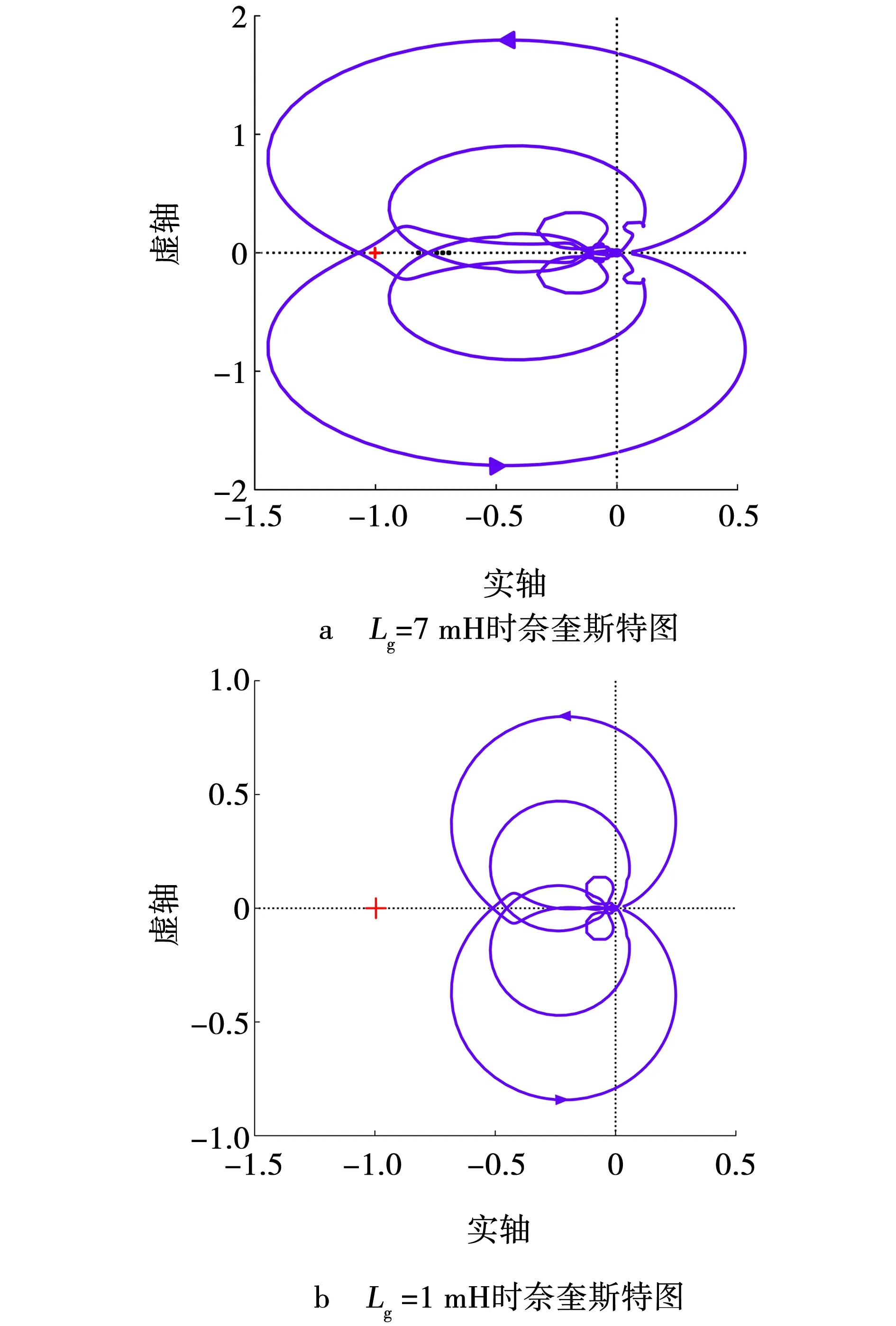
图9 不同Lg值的Gk奈奎斯特图Fig. 9 Nyquist plots of Gk for different Lg

3 仿真验证

3.1 仿真算例及参数

为了验证文中所建立导纳模型的准确性，在仿真软件中搭建了如图10所示的并网逆变器仿真模型，逆变电路采用SVPWM技术，电网电压有效值为110 V，直流电压400 V，d轴参考电流为6 A，q轴参考电流为0，仿真模型其余参数为直流侧电容4 mF、直流侧电阻1 Ω，网侧滤波电感7 mH，锁相环比例系数2.4、积分系数500，电流环比例系数35、积分系数8 000，电压环比例系数0.5、积分系数11。通过改变电网侧电感大小，同时调整控制器参数，使三相电流发生振荡，观察并网电流波形。

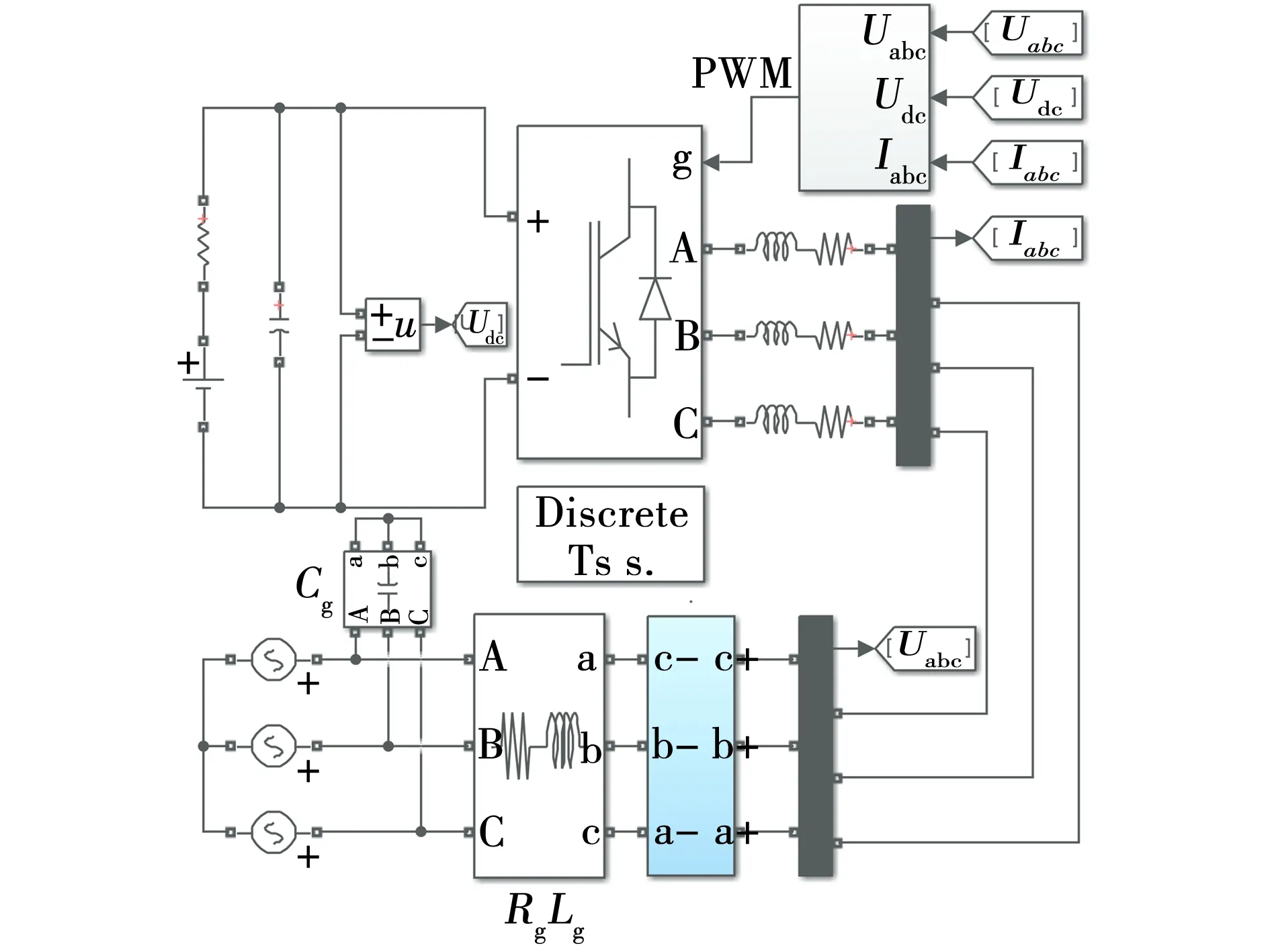
图10 仿真模型Fig. 10 Simulation model

3.2 仿真结果

电网电感Lg=1 mH时，此时短路比为9.2，系统稳定运行，此时，谐波畸变率(THD)为2.97%，符合并网要求。电网条件不变，增大电压环比例系数，电流波形如图11所示。电流中存在着幅值占比η为2%扰动量，对电流整体波形的影响较小。

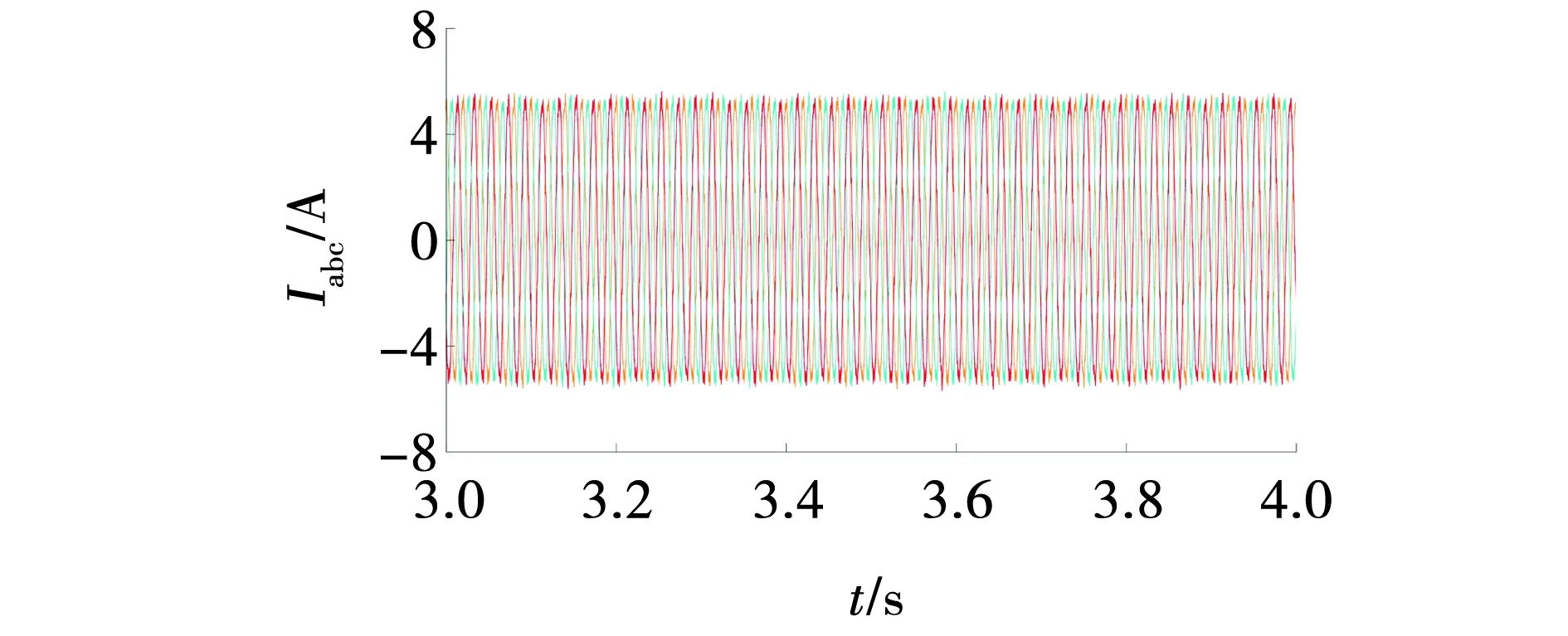
图11 Lg=1 mH时并网电流波形Fig. 11 Grid-connected current for Lg=1 mH

电流的FFT分析，由图12可知，并网点电流中存在着频率约为32 Hz的扰动分量，同时还存在频率约为68 Hz的耦合分量。该仿真结果表明，当并网点存在频率为32 Hz的正序扰动时，会产生频率为68 Hz的耦合分量。

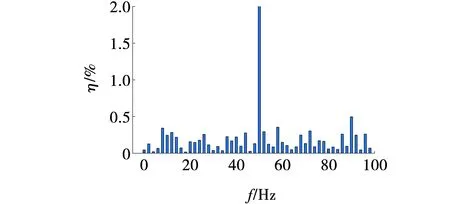
图12 Lg=1 mH时电流FFT分析结果Fig. 12 Results of FFT analysis for Lg=1 mH

在t=5 s时突然改变电网电感，令Lg=7 mH，此时短路比为2.4，电流波形如图13所示。此时三相电流的振荡更加明显。电流的FFT分析结果如图14所示，此时THD为15.82%。

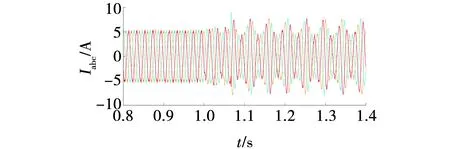
图13 Lg=7 mH时并网电流波形Fig. 13 Grid-connected current for Lg=7 mH

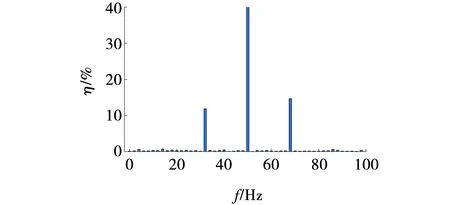
图14 Lg=7 mH电流FFT分析结果Fig. 14 Results of FFT analysis for Lg=7 mH

耦合效应相应增强，32 Hz的电流分量约占基频分量的12%，68 Hz的电流分量约占基频分量的15%，扰动量占比进一步提高，耦合分量稍大于扰动量，并网逆变器稳定性进一步下降。以上仿真结果表明在弱电网条件下，并网逆变器的稳定性更差，容易在32 Hz左右发生振荡甚至失去稳定。

4 结 论

(1)采用复矢量阻抗分析法，建立了DDSRF-PLL的并网逆变器的导纳模型，与SRF-PLL的并网逆变器的导纳模型进行了对比，发现在低频段DDSRF-PLL所产生的干扰幅值更大，且相角相差90°～180°。

(2)根据导纳模型推导出扰动电压到扰动电流的开环传递函数Gk，电网电感由1 mH增大至7 mH时，短路比由9.2升高至为2.4，电网强度变弱，奈奎斯特曲线逐渐包围(-1，j0)点，并网电流出现32 Hz的振荡，系统稳定性开始下降。