基于深度强化学习与流固耦合技术的鱼类自主游动行为模拟

李涛，张春泽*，但云峰，赵旭

(1.重庆交通大学西南水运工程科学研究所，重庆 400010；2.重庆交通大学水利水运工程教育部重点实验室，重庆 400074；3.重庆西科水运工程咨询中心，重庆 400074)

鱼类身体两侧的侧线感受器官对水流的刺激尤为敏感，能帮助鱼确定水流的速度和识别方向，从而使其在复杂的流场环境下完成捕食运动或者以选择更省力的游泳动作[1]。此类自主决策行为对鱼类生存和繁衍有着重要意义，一直是生态学与仿生领域的研究重点。冯亿坤等[2]基于计算流体力学(computational fluid dynamics，CFD)方法建立了鱼类游动流固耦合模型，模拟了机器仿生鱼巡游游动，并系统分析了迅游过程中鱼体的受力和反卡门涡街的变化情况。胡瑞南等[3]基于Fluent的用户定义函数(user-defined function，UDF)动网格技术模拟了不同尾巴摆动模式的机器鱼周身的流场压力及鱼体受力等水动力性能，解释多关节机器鱼的相对优势。Wolfgang等[4]通过求解速度势的Laplace方程和压力的非定常Bernoulli方程，研究了游动的巨型斑马鱼的流场。Ramamurti等[5]采用动态非结构网格技术模拟鱼胸鳍拍打过程，分析鱼周流场和鱼体受力。上述研究为鱼类游动数值模拟实验提供了丰富的数值模拟经验和研究成果，但从研究手段本身来看，只能模拟鱼体的被动运动，无法实现鱼体根据流场与目标对运动行为的主动控制。

为实现对鱼类自主行为决策的模拟，有学者引入人工神经网络的方法对鱼类游泳进行数值研究[6-7]，该方法通过对大量已有游泳样本的学习进化出合理的、稳健的游泳策略，但需要大量的实际观测数据，观测数据的获取需耗费大量人力物力。为此，又有学者尝试采用深度强化学习算法来作为鱼类游动数值模拟的控制器[8-9]，并结合传统数值模拟方法耦合流场，此类方法能自动生成学习所需的经验样本，克服了传统人工神经网络法需要大量实际观测样本的缺陷，并且实践成本低、鲁棒性强，能够实现自优化。

基于此，通过浸没边界格子Boltzmann方法实现鱼体游动流固耦合数值模拟模块，提供训练数据和执行游动指令；基于PyTorch机器学习库，选取DQN(deep Q network)深度强化学习算法实现鱼脑训练学习和决策任务，建立一个智能鱼训练、决策、执行耦合平台，最后通过新建平台，对鱼类典型捕食运动以及卡门游动由易到难的训练与模拟，并分析该平台的可靠性与实用价值。

1 流体、固体控制方程与数值解法

鱼体与流场之间的互馈作用通过浸没边界LB(Lattice Boltzmann)流固耦合方法进行模拟，实时将鱼体状态与流场信息反馈给深度强化学习模块进行训练，根据训练结果作出下一时刻鱼体决策。

1.1 浸没边界LB方法

浸没边界LB方法是一种高性能、高精度的流固耦合模拟方法，该方法属于基于Lagrange观点捕捉运动界面，非常适用于模拟鱼类游动、昆虫振翅、心脏搏动等柔性结构的大变形流固耦合问题，已在许多流固耦合问题上获得了较为成功的应用[10-11]。

在浸没边界-格子Bolzmann法中，流体运动由离散的格子-Bolzmann方程控制，方程右端的力项采用Cheng格式，可表示为

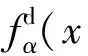
(1)

对于浸没边界，则采用拉格朗日法可表示为

(2)

(3)

式中：Ωf为流体区域；Γb为浸没边界；s为浸没边界的体型长度；x、f、u分别为流体节点的坐标、体积力、速度，是定义在流体区域Ωf上的欧拉变量；X、F、U分别为浸没边界的节点坐标、作用力线密度和速度，是定义在浸没边界Γb上的拉格朗日变量；δ为狄拉克函数，是流固耦合实现的关键函数，它既可以将式(2)中的流体速度u插值得到浸没边界U的速度，也可以将式(3)中浸没边界的作用力F扩散至周围的流体节点得到f。

在浸没边界法里，F的计算精度会影响无滑移边界条件的满足程度，根据文献[10]提出的方法，浸没边界作用力通过一系列迭代修正，来逼近真实值，其计算公式为

(4)

式(4)中：n为迭代步数；Ud(s,t)为浸没边界在流体中的实际速度；Un(s,t)为第n迭代步的临时速度；Fn(s,t)为第n迭代步的力项；Δt为时间步长。

通过式(4)，可以不断计算迭代后的F(s,t)值，然后将最终迭代完毕的F(s,t)值添加到格子Bolzmann方程[式(1)]中。

对于浸没边界法的流固耦合问题，需要考虑浸没边界的平动以及转动，控制方程为

(5)

(6)

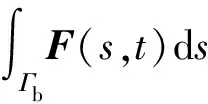
模拟真实鱼类的运动，需要以鱼体运动方程控制鱼体(即浸没边界)，并将波动从笛卡尔坐标系转换到鱼体运动的随体坐标系中。不考虑除尾鳍外其他鱼鳍的直接作用，简化后鯵科类鱼体波曲线可表示为[3]

(7)

(8)

(9)

1.2 深度强化学习算法

深度强化学习算法因其交互学习性、鲁棒性、决策稳健等优点，近年来已广泛应用于电力系统优化[12]、分布式传感网络[13]、智能棋类运动[14]、无人驾驶[15]、各类机器人控制[16]、调度科学[17]等领域，成为通用人工智能(artificial intelligence，AI)的解决方案之一。

其中，强化学习(RL)是一种通过不断与环境互动从而自提升的算法，最终目的是为了找到当前环境下的最优策略。评价强化学习训练效果的客观指标为智能体在与环境互动时获得的奖励多少，主观指标为智能体是否按照预期效果完成给定的任务。如果智能体在训练回合内获得奖励数越多，说明智能体学习到了按照期望设定的行动策略，在此策略下行动的智能体就越有可能完成给定的任务。设状态为sstate，行动为a，在基于策略π选择行动的情况下，行动的概率为π(a|sstate)，最优策略要使得当前行动的价值最大化，有

(10)

式(10)中：π(a|sstate)为状态sstate下的最优策略；Q(a|sstate)为状态sstate下采取动作a的价值；A为所有动作的集合。

传统的Q学习的策略价值通常用Q函数来表示，Q(st,at)的迭代更新过程为

Q(st,at)←Q(st,at)+αlearn[rt+1+

(11)

式(11)中：Q(st,at)为Q函数；rt+1为奖励值；αlearn为学习率；γ为折扣系数。

为了应对传统强化学习算法使用表格储存状态而导致的维数灾问题，学者们将深度学习技术应用到了强化学习中，并使得强化学习的性能取得了突破性进展。深度学习(DL)是一种机器学习模型，能够学习数据的内在规律和表示层次。相对于传统的机器学习方法而言，深度学习可以通过多层神经网络进行多次特征转换，获取数据表示的高维特征。深度强化学习则结合了深度学习的感应技能与强化学习的决策技能，它通过强化学习与环境进行互动，根据环境获得的反馈对深度学习参数进行调整。DQN算法作为深度强化学习算法的一种，具有以下特性：①利用神经网络生成每个动作Q价值；②通过记忆库实现经验回放机制，更加贴近现实中大脑的概念；③用目标网络和估计网络两套神经网络进行训练，并且隔一段时间利用估计网络来更新目标网络的参数，切断了神经网络的实时相关性，并提升了网络性能。

2 建立流体求解器与深度强化学习的耦合平台

2.1 耦合框架

整个耦合框架分为智能鱼大脑、智能鱼肉体和流场生境，具体为:①智能鱼大脑经过学习训练后通过最优决策发出动作信号控制智能鱼肉体；②智能鱼肉体接收动作信号，并在流场生境中采取相应动作；③通过流固耦合模块计算流场、鱼类当前状态等信息后，流场生境传递当前时刻的状态信息和奖励信号给智能鱼大脑作为环境反馈；④重复①～③，整个过程形成闭环控制，图1为耦合系统框架。

图1 耦合系统框架

2.2 耦合流程与伪代码

考虑到科学计算效率问题，用于模拟鱼体运动与周围流场环境的模块代码通过C++语言编写；考虑到代码开发难度，深度强化学习训练与决策模块代码通过Python语言编写。同时，为保证训练与执行过程的智能化与连续性，使智能体能够通过与环境互动，以进行自动“强化”，采用Windows 共享内存技术实现不同语言不同模块的进程通信，耦合系统的伪代码如下。

初始化超参数初始化目标网络参数θ和估计网络的参数θ′1:For episode = 1:Ndo2: C++端初始化流场、鱼体状态信息sstart,Python端初始化系列超参数3: For time = 1:Tdo4:C++端将sstart传递给Python端,然后Python端根据sstart获得一动作a,并把a传递给C++端;5:C++端根据a求解Δt时间步后,记录下当前状态s′、奖励r,并打包发送给Python端;6: Python端将记忆矩阵[s,s′,a,r]存入记忆库、M,并更新:s←s′7: Python端从记忆库取出batch批数量的样本进行训练,根据Ad-am优化算法更新估计网络参数8:Python端每隔Δt′时间步,将估计网络的参数θ拷贝到目标网络θ′11: End for12: Python端将训练后的神经网络和记忆库储存到本地磁盘,方便后期调用13:End for

整个算法的时间复杂度为O(n2)，在可接受的范围内。

3 流固耦合模块验证-小球下沉问题

在所搭建的系统平台中，流固耦合模块是训练场景预设和方案执行的承担者，其数值精度与模拟效果直接影响到深度强化学习过程有效性。为此将采用经典小球入水下沉算例对其进行验证。

相关参数设置参考了文献[11]中的小球下落案例，流场区域为宽2 cm、高8 cm的矩形，离散为201×801的均匀网格。水体的运动黏度为υ=1×10-6m2/s，密度ρ=1 000 kg/m3。重力加速度g=9.80 m/s2。两个半径均为0.1 cm的等大小球同时释放，二者初始时刻位置分别为[0.999 cm，7.2 cm]和[1 cm，6.8 cm]，释放之后小球将因重力作用下沉。小球密度ρs=1 010 kg/m3，均离散为125个拉格朗日点。为确保计算代码不会因小球运动控制方程刚性而失稳，此处使用高阶精度变步长Gear积分方法更新小球运动轨迹。

根据前人实验的结果，静水中两小球下沉会经历一个DKT(drafting，kissing，tumbling)的经典运动学过程。如图2所示，在接触阶段之前，小球维持一定距离运动，这一阶段被称为追逐阶段，持续到约0.8 s；之后两小球开始缓慢靠近并于约1.5 s碰撞在一起，进入接触阶段，之后在碰撞力的作用下，两球缓慢远离中轴线向水槽两侧运动,在2.5 s时，小球进入碰撞翻滚阶段。从图3、图4可以看出，本次模拟的结果与吴家阳等[11]、Feng等[18]的结果基本一致，可以说明数值计算模块的可靠性。

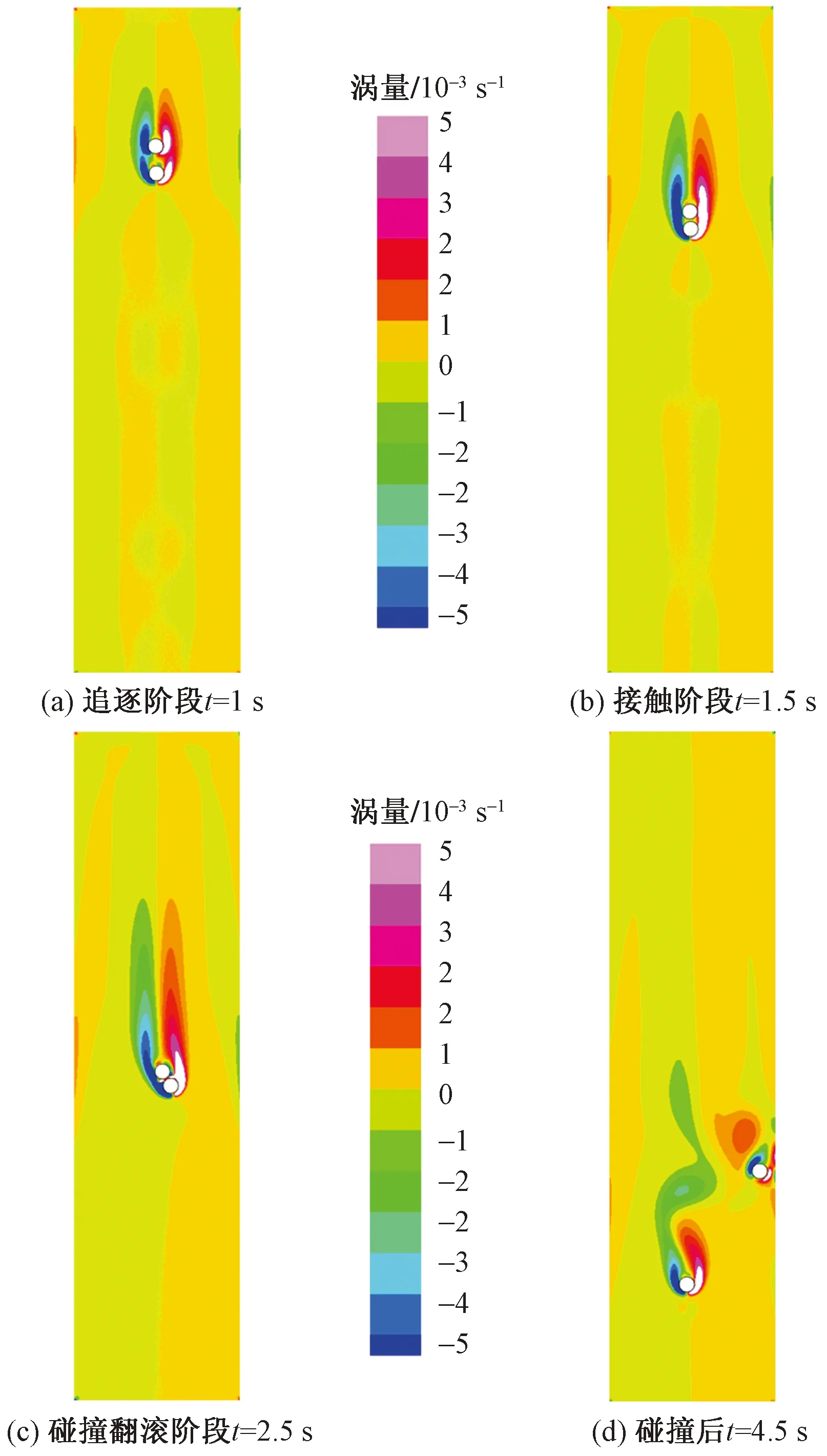
图2 小球DKT典型运动过程

图3 小球横坐标随时间变化

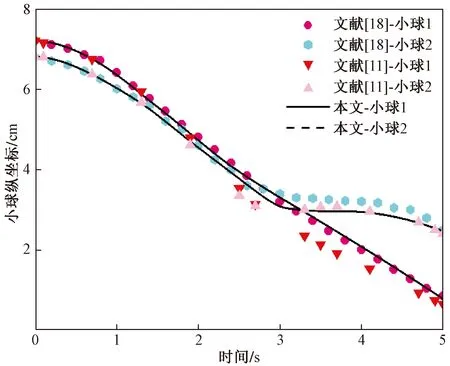
图4 小球纵坐标随时间变化图

4 鱼类典型游泳行为的强化学习实验

针对拟定的运动情境，通过深度强化学习模块和流体求解器模块的不断交互，以提升深度神经网络的性能，观察智慧鱼是否能以预期目标完成游泳任务，并分析所建耦合平台的使用效果。

4.1 实验环境介绍

实验所使用的硬件环境和软件环境如表1所示。

表1 硬件及软件环境配置

在鱼类捕食运动的训练实验中，较小的深度神经网络学习率能够保证训练结果的可靠性，设置学习率αlearn=0.001，时间折扣因子是强化学习的一个超参数，设置得越大，智能体越具有考虑长远未来奖励的能力，设置γ=0.99，Epsilon-Greedy贪婪因子设置为0.1，单批次训练处理样本数Batch size=32。深度神经网络总层数为5层：其中输入层节点数为4；隐藏层共3层，每层节点数128；输出层节点数为3。给神经网络投喂状态矩阵[s1,s2,…,sn]，就可以从输出层得到每个动作的动作价值矩阵[Qa1,Qa2,…,Qan]。强化学习模块的奖励规定如下。

(1)对于捕食游动，若智能体与食物的夹角逐渐减小，说明鱼体行进在正确的轨迹上，则奖励为+1，反之奖励为-1；若智能体能够成功获取食物，则奖励为+20，如果智能体碰到边壁或吃到食物，则回合结束。

(2)对于卡门游动，总的奖励被分解为奖励1和奖励2：对于奖励1，其大小与鱼体游泳所消耗的能量成反比，游泳消耗能量越多，奖励越低，对于奖励2，如果鱼体在一个摆尾周期内前进或者后退了50个格子单位，则说明当前的采取的游泳策略无法在流场中维持稳定的游动，奖励为0，反之奖励为+1。

对于流体求解器模块，为方便展示计算结果，将所有物理单位换算成无量纲格子单位，并以“*”表示实验中的无量纲参数，采用500×200正交笛卡尔网格离散计算域，网格数量共100 000。水体密度ρ*=1，采用NACA0012流线翼型表示鱼体，同时用999个拉格朗日点离散鱼体，考虑鱼体在浮游的时候鱼泡充水，实际密度与水接近，故取密度为1.05。在求解过程中，鱼尾的摆动参数则由鱼体自主决策，鱼类推进参数由使用式(5)、式(6)求得水体对鱼的合力及合力矩。

4.2 捕食游动

在此算例中，鱼体在静水流场中捕食，目的是通过训练让鱼体能够以不同的初始偏角度出发、同时以最优路径(路程最短)吃到食物。

本次训练共设置4种工况，不同工况赋予不同的初始偏角度，分别为-10°、+10°、+20°、+30°，详细的工况设置如表2所示，偏角度的定义是鱼体质心与食物中心的连线和鱼体前进方向的夹角，角度符号的定义如图5所示。

表2 不同工况下的初始偏角度

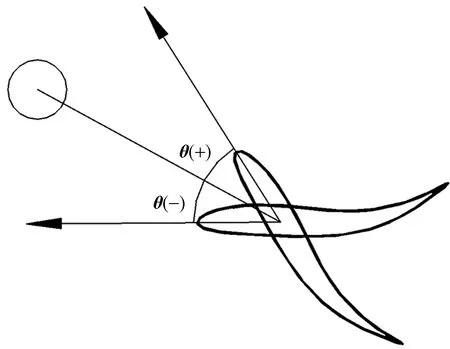
θ(+)为鱼体质心和食物连线的夹角沿顺时针旋转得到当前鱼体前进的方向矢量；θ(-)为鱼体质心和食物连线的夹角沿逆时针旋转θ°得到当前鱼体前进的方向矢量

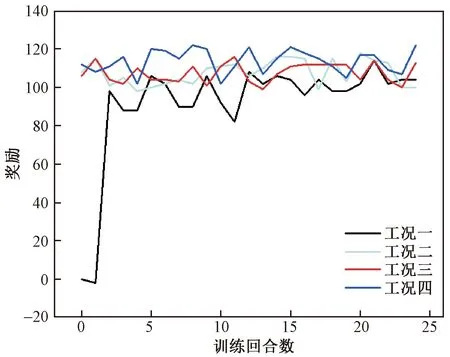
智能体每回合训练获得的奖励如图6所示，值得注意的是，本算例中首先使用-10°的初始偏角进行训练，然后将训练好的鱼给予不同的初始偏角，以验证训练结果的可靠性，所以工况二～工况四的奖励一开始就能达到很高的水平。在工况一的训练条件下(图6)，前两个回合，未学习的鱼体获得奖励极少，而自第二回合后，鱼体获得的奖励产生一个陡增趋势，说明神经网络经过两个回合的自优化已经学习到了一定知识，经过学习鱼体能够在捕食环境中取得较高奖励。可见，合理设置奖励、观测状态以及神经网络权重归一化都有助于加速神经网络的收敛，这也是本算例中鱼体仅用两个回合就优化到良好状态的原因。不同工况下鱼体的代表运动轨迹如图7所示，以鱼头顶点作为监测点，训练之后，相对于食物具有不同初始偏角的鱼体都能够

虚线圆圈为预先设定好的智能体的运动目标终点

虚线圆圈为预先设定好的智能体的运动目标终点

以最优轨迹小幅度迂回到达目标点。在自然界，水生生物、飞行器以及水下航行器等的推进过程中，经常从其尾迹中可以观察到一系列尾涡结构，而它们常常利用这些结构来实现自推进，降低运动过程中的能量损失。鱼体静水捕食时的流场涡量云图如图8所示。

t*为无量纲时间

为了使鱼体尝试更加富有挑战性的捕食任务，令食物在鱼游动的同时改变位置，模拟食物运动时鱼类的捕食情况，但不考虑食物对流场的水动力学影响，除此之外，食物的初始位置以及鱼体初始偏角均与前述静水问题相同。

本例同样使用初始偏角为-10°的工况进行训练，并将训练好的网络施用于不同偏角工况。鱼体训练获得的奖励如图9所示。在工况一下，前两回合，鱼体基本未获得奖励，但第二回合之后，鱼体的奖励有和3.2节相同的趋势，在第8回合后，鱼体获得的奖励的平均水平显著高于前8个回合，说明网络已训练成熟，鱼体能够在食物运动的环境下获得较高的奖励。

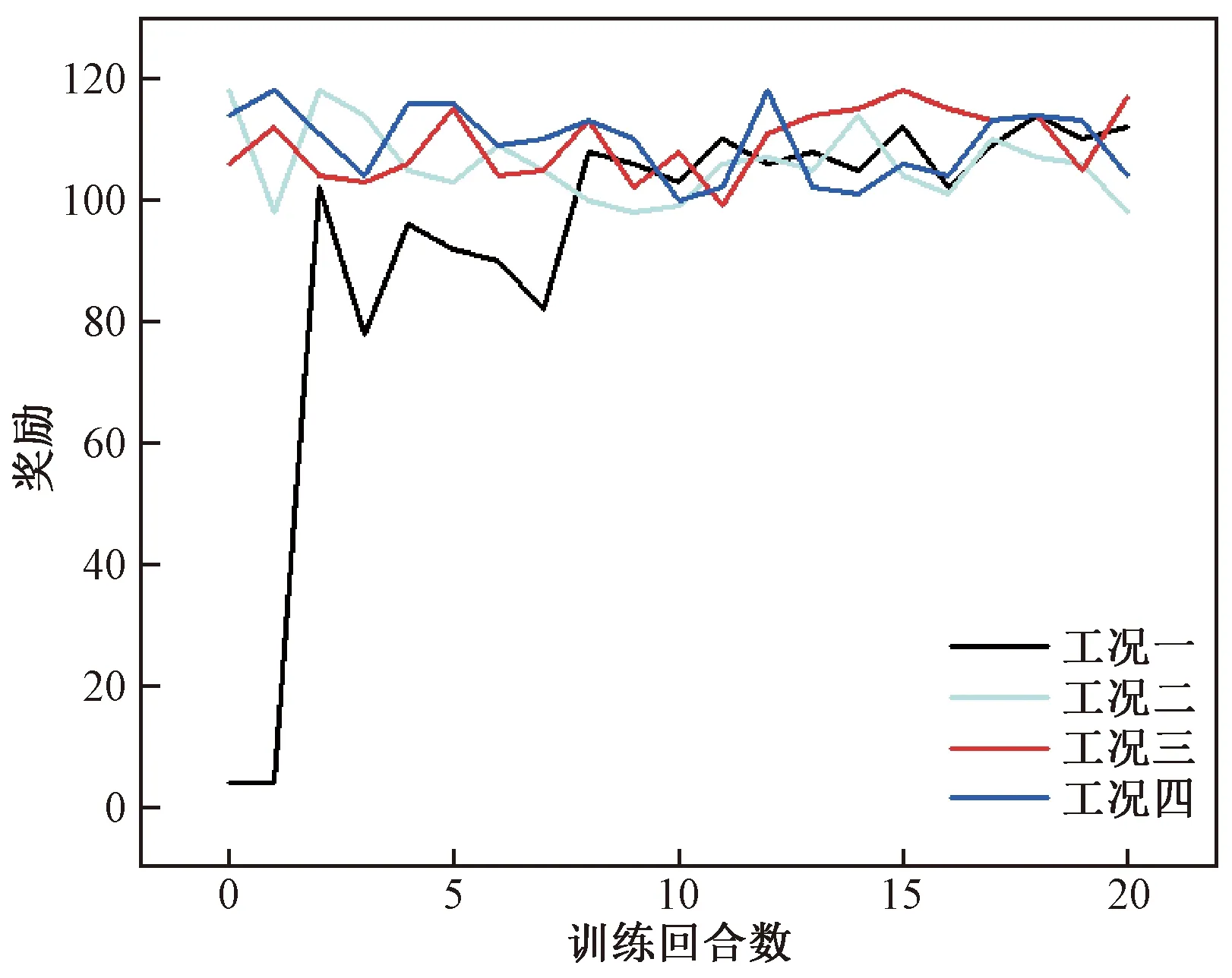
图9 智能体训练每回合获得的奖励数

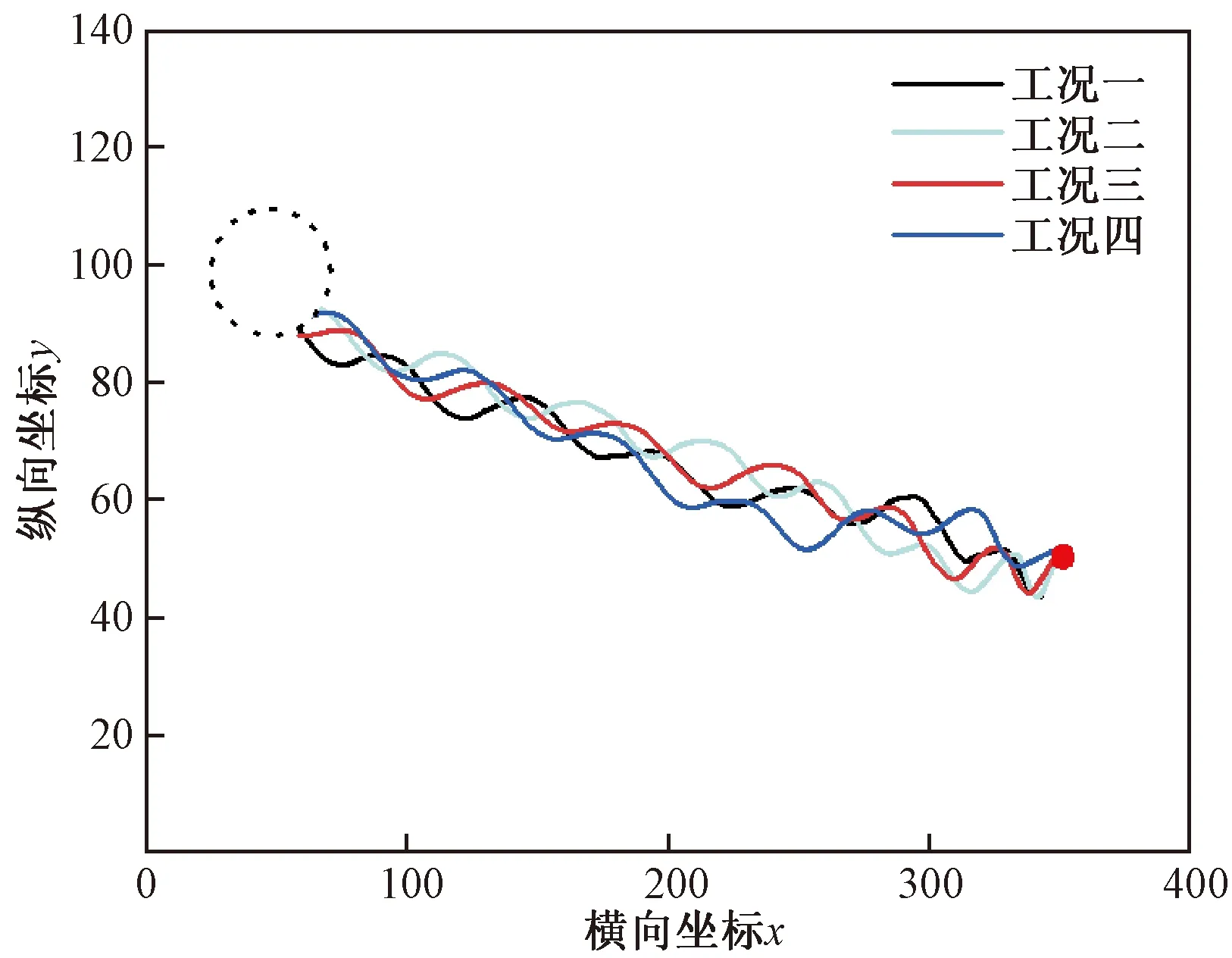
图10绘制了食物运动时、不同初始捕食角度鱼体的运动轨迹。当鱼体发现目标在移动时，会实时对自身与食物相对位置进行判断，及时调整运动状态以至于能够在当前环境中获取最大的奖励，保证自身处于距食物最近的路径上，最后顺利获取食物。

虚线圆圈为预先设定好的智能体的运动目标终点

需要说明的是，所建的深度强化学习模块还相对初级，鱼脑并无对食物运动轨迹预判的能力。此处鱼体能够吃到食物，很大程度上要归因于食物运动速度较鱼体更低。

4.3 卡门游动

已有实验表明，当雷诺数Re在300～150 000时，流体经过静止的障碍物会产生一系列漩涡尾迹，称为卡门涡街[19]。在卡门涡街中，鱼类游泳时会采用一种全新的游泳步态，以同步自身身体的运动与旋涡脱落频率从而达到节省能量的目的，这种独特的运动模式被称为卡门步态，其特点是尾拍频率较低，身体具有较大的侧向位移[20]，研究鱼类的卡门游动可以解释鱼类游泳的节能机制。本算例中，流场特征雷诺数为300，上游为速度入口边界，在距离上游100格子单位处放置一直径为40格子单位的柱子，速度入口无量纲流速U*=0.15，下游为自由出流边界，上下壁面均为无滑移边界，涡街漩涡脱落频率fstreet为0.001。计算目的是通过训练让鱼体找到在非定常漩涡流场中最佳的尾拍频率，从而在涡街中进行更加稳定、节能的游动，对于复杂流场下的游动，需要合理设置奖励函数才能保证训练的合理性与可靠性，智能体才能按照预期目标完成指定的游泳任务。此处奖励函数的设置同时考虑了鱼在流场中游动耗费的能量和鱼在流场中保持的位置。

图11为每回合训练鱼体获得的奖励图，由于流场环境复杂，卡门游泳的鱼体奖励图相对于捕食运动算例并不稳定，奖励在第10回合后出现了较为剧烈的波动，但后半段奖励的平均值仍然要远远高于前5回合的奖励值，说明鱼体通过训练学习到了正确的游泳策略。鱼体一个尾拍周期内的运动的涡量云图(图12)可知，鱼体经过训练后能够以比较稳定的步态在涡街中运动，鱼体尾拍频率约为0.001，与涡街脱落频率一致。

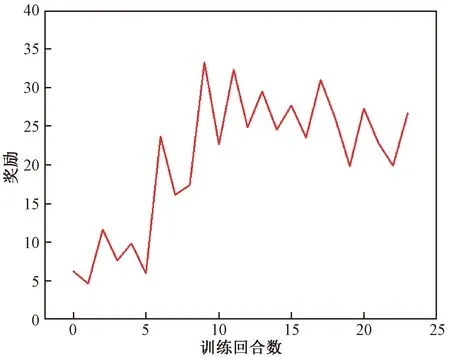
图11 卡门游动算例智能体训练每回合获得的奖励数

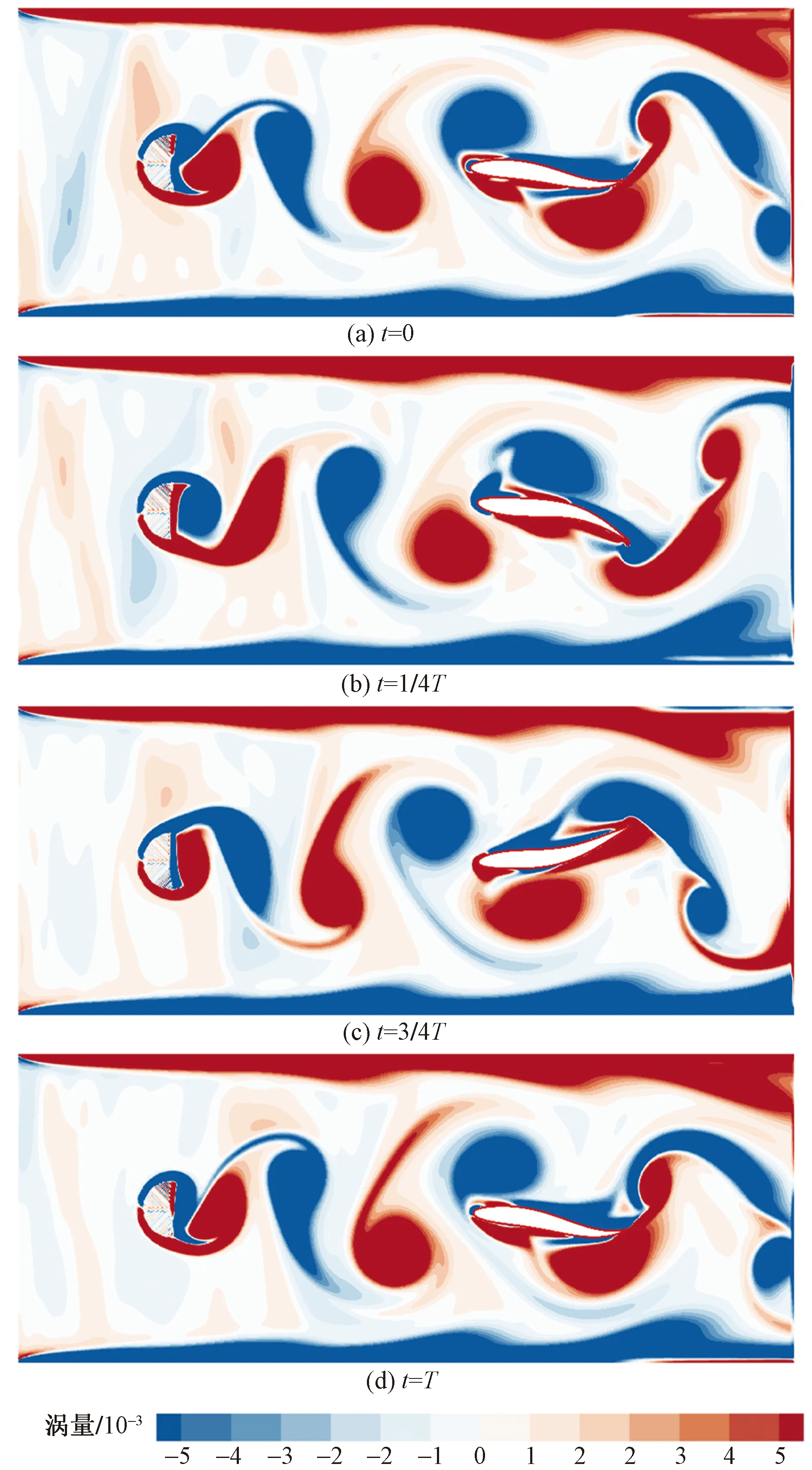
t为鱼体当前的运动时间；T为鱼体的尾拍周期

从鱼体游泳位置的决策上来看，鱼体为了节省游泳能量，会选择在两排涡街的夹缝区域进行游动，从而利用涡街中交替的漩涡获取能量；从鱼体尾拍频率的决策来看，选择与涡街脱落频率一致的尾拍频率能够帮助鱼体交替利用前后漩涡的能量，对漩涡能量的利用率能够达到比较高的水平。

设置与卡门游动同样的流场边界条件，不设置D柱，开展鱼体自由游动研究。此时鱼体趋流运动，通过主动提高摆尾频率和出力来维持在流场中的游泳位置。

图13展示了鱼体卡门游动和自由游动时的鱼体瞬时功和总功。自由来流工况下的鱼瞬时功更大，并且瞬时功峰值间距相对于卡门游动工况下间距更小，说明鱼体在该工况下采用了更高的摆尾频率，来获得更大的出力。在整个游泳过程中，卡门游动工况下鱼体无量纲总出力为55.13，自由来流工况下鱼体无量纲总出力为169.21，是卡门游动工况总出力的306.9%，可见鱼体在采用卡门步态时能大幅减少做功出力。这种节能高效的游动方式可使鱼体能够利用涡街中漩涡的低涡量高流体剪切应力区节省游动能量。

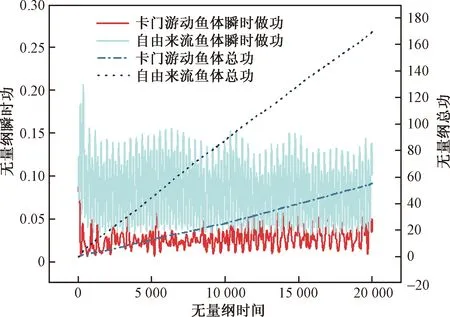
图13 鱼体在不同来流条件下游动的做功

5 结论

建立了一个基于深度强化学习与流固耦合数值模拟的智能鱼训练、决策、执行平台。通过浸没边界格子Boltzmann方法实现鱼体游动模拟，提供训练数据和执行游动指令，通过DQN深度强化学习算法实现鱼脑训练学习和决策任务。利用该平台对鯵科鱼的捕食游动和卡门游动进行模拟，得出如下主要结论。

(1)耦合计算流体力学与计算机人工智能方法研究鱼类行为学问题。所搭建的平台采用C++/Python混合编程，兼具高性能运算效率、易于开发维护的特点，同时采用模块化编写函数，易于后期的更新和功能的完善。

(2)经过大量的训练，实现了智能体的捕食游动以及卡门游动实验。在捕食游动实验中，鱼体能够以不同初始偏角度以最优路径到达食物所在位置，说明强化学习模型收敛性良好；在卡门游动实验中，鱼体的尾拍频率接近涡街脱落频率，并以极其稳定的步态在涡街中运动，从功能关系角度的分析表明鱼体采用此步态更节省能量。

(3)深度强化学习算法可以通过不断与虚拟环境之间互动以进行高效率、自主学习，同时，数值求解器可在短时间内生成大量用于强化学习模块的训练数据，无须再通过实验等方式获取。深度强化学习技术和数值模拟技术相结合，可为水利工程、生态环境工程等领域的数字孪生提供技术支持。