长输管道输油鲁尔泵内部流场特性研究

谯林峰，莫丽，毛良杰，梁玉林

(1.西南石油大学机电工程学院，成都 610500；2.西南石油大学油气藏地质及开发工程国家重点实验室，成都 610500；3.川庆钻探工程有限公司钻采工程技术研究院，德阳 618000)

鲁尔泵是一种带导流器的双吸输油离心泵，其组成的输油机组是“西油东送”中油气集输系统中的关键设备，鲁尔泵的稳定运转直接影响着输油管路的输送效率。但鲁尔泵在特殊工况下运行时，会发生剧烈的湍流流动，影响鲁尔泵的安全可靠使用，故有必要对其开展流场特性研究。

鲁尔泵的内部流动为非定常不可压缩黏性流动，在偏离设计工况时，叶轮、导流器内均会出现剧烈的湍流流动，会对输油机组的水力性能产生重大影响。如今鲁尔泵的理论分析与实验研究存在许多困难，多数研究采用数值模拟方法进行。Shi等[1]运用二维和三维全流道数值模拟的方法对带有导叶的离心泵内由叶轮和导叶相互干涉引起的压力脉动特性进行了研究。Majdi[2]采用三维数值模拟方法对带有蜗壳的离心泵内的非定常流体流动进行了研究，并且详细分析了泵内各处的压力脉动变化机理。Spence等[3]采用不同方法对双吸式离心泵两叶轮叶片交错角的影响进行了研究,发现对双叶轮的叶片进行一定程度交错会明显降低泵内压力脉动。袁寿其等[4]在对低比转速离心泵的改进试验中通过增加泵的流量和比转速可以大幅增加泵的效率。随着计算流体力学(computational fluid dynamics,CFD)软件在中国的普及与数值模拟方法的发展，越来越多研究者将其应用于离心泵流场研究。曹蕾等[5]针对一种多级离心泵的导流器导叶内存在脱流、漩涡的现象，通过几种导叶模型的三维湍流流场进行分析，获得了较优模型。周邵萍等[6]对一种多级离心泵导叶内部流场分析并对水力损失进行评测，并在此基础上提出了优化的导叶设计。江伟等[7]还通过流场分析指出了半高导叶对离心泵压力脉动性能的影响规律，采用半高导叶能有效改善内部流动的稳定性。汪家琼等[8]通过改变多级离心泵的叶轮和导叶的组合方式，进行流场分析，得出多级离心泵水力效率下降主要是由流道内的涡流过大所产生。曹卫东等[9]采用正交试验设计法对两级离心泵径向导叶进行水力优化，得出了对离心泵性能影响最大的参数是导叶喉部面积。张玉良等[10]利用Fluent研究离心泵的叶轮采用不同出口安放角下的性能，论证了采用大出口安放角时泵的水力损失相对较大。

综上所述，目前对离心泵的分析主要集中于多级离心泵的流场分析与结构优化，而鲁尔泵是单级双吸离心泵，带有特殊的导流器，与一般离心泵相比其总体结构更为复杂，其叶轮中高速流体更易使导流器焊缝结构失效，并且关于鲁尔泵的叶轮-导流器动静干涉特征规律及导流器入口叶片结构失效机理尚不清楚。因此，针对上述问题，以ZLM型鲁尔泵为例，采用基于SSTk-ω(k为湍动能，ω为耗散率)湍流模型对鲁尔泵内部非定常流场进行数值分析，在不同流量工况下探讨了鲁尔泵内的压力分布规律和各过流部件的内部流场特性，以期对鲁尔泵的可靠运行及优化提供科学依据。

1 ZLM鲁尔泵计算模型的建立

1.1 流动控制与湍流模型

由于鲁尔泵的内部流动为非定常不可压缩黏性流动，求解雷诺平均的N-S(Navier-Stokes)方程成为解决问题切实可行的手段[11]，雷诺平均控制方程为

(1)

式(1)中：ρ为密度；t为时间；xi为流体流动方向坐标，i=1,2,3；ui为速度分量。

但该方法的缺陷在于:在平均运动中湍流脉动量的影响即雷诺应力是未知的，需要建立湍流模型。选择SSTk-ω湍流模型，该模型能较为准确地模拟离心泵内部流场，并在一定程度上考虑了各项异性效应和湍流旋涡特性。

湍动能k方程为

Gb-ρε-YM+Sk

(2)

式(2)中：xj为流体流动方向坐标，j=1,2,3；μ为动力黏度；k为湍流动能；ε为湍流耗散率；μt为湍流黏度；Gk为由于平均速度梯度产生的湍流动能产生项；Gb为由于浮力产生的湍流动能产生项；YM为可压缩湍流中的波动膨胀对整体耗散率的贡献；σk为k的普朗特数，σk=1.0；Sk为用户自定义源项。

湍能动能扩散率ε方程为[12]

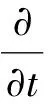
(3)

式(3)中：Sε为用户自定义源项；C1ε、C2ε、C3ε为常数，C1ε=1.44，C2ε=1.92，C3ε=1.3；σε为ε的普朗特数，σε=1.3。

只有认识到著作权为仅赋予著作权人许可或禁止他人以法律规定的方式利用其作品，才是对著作权正确的理解。如何理解《著作权法》第10条要具体规定著作权人的16项具体权利，而不是像物权那样概括规定物权人的权利？这正是一种对著作权人垄断其作品的限制，使其只能限制他人以有限的特定方式利用其作品，而这以外的其他利用行为，如对作品的阅读、背诵，乃是公众的自由，以体现“法无禁止即自由”，保证公众对作品的自由接触权，进而促进作品的流通，最终达到知识产权法促进知识和信息的广泛传播，促进经济的发展和科技、文化进步⑲ 冯晓青著：《知识产权法利益平衡理论》，中国政法大学出版社2006年版，第82页。的最终目的。

1.2 鲁尔泵的扫描建模

分析模型选用ZLM IP 530/06型鲁尔泵(简称鲁尔泵)，图1为鲁尔泵的剖面视图，流体从叶轮的左右两个入口吸入，从导流器出口排出。

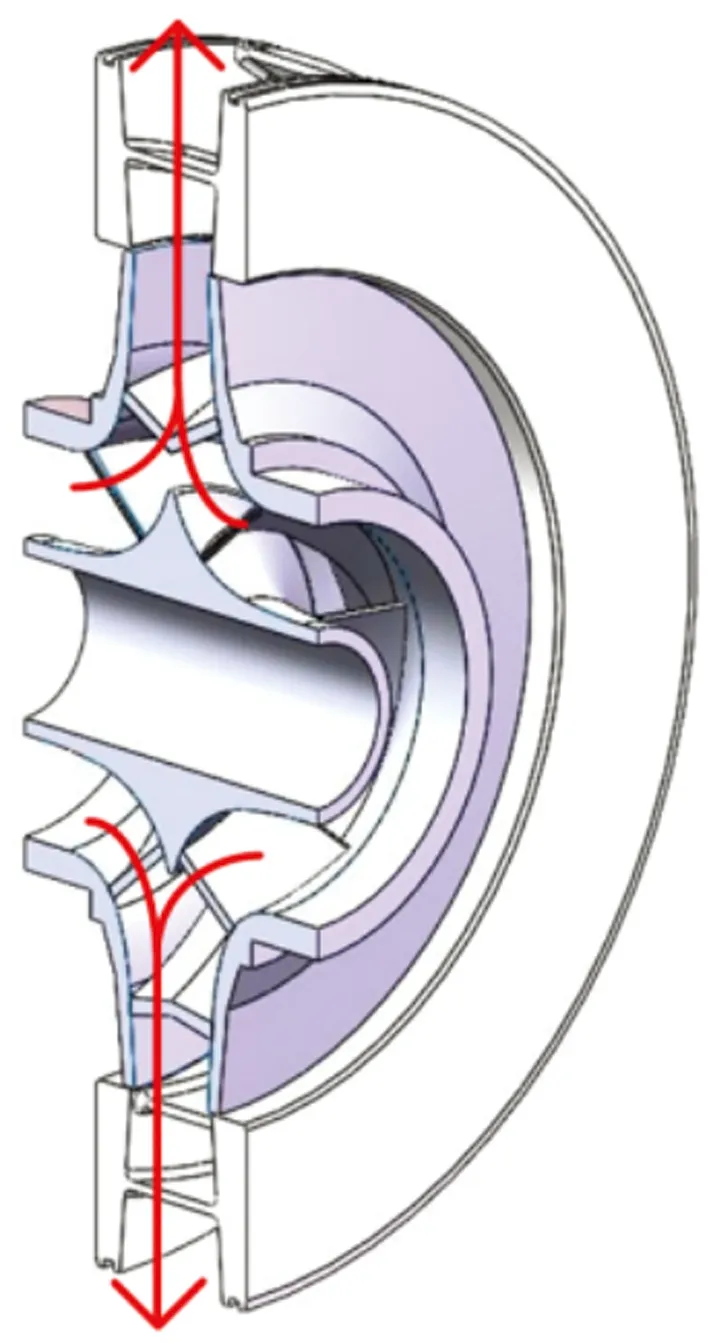
图1 鲁尔泵模型工作原理图

该泵作为“西油东送”工程中站厂内输油主泵，有高扬程的特点。采用高精度三维坐标扫描仪对其进行扫描测绘。根据测绘结果，其主要尺寸参数如表1所示，材料特性如表2所示。为了方便对模型进行更改，采用SolidWorks对ZLM鲁尔泵导流器进行建模，并在Space Claim中利用布尔运算提取其流体域，再导入进ANSYS Fluent中进行数值分析。鲁尔泵三维模型如图2所示，装配模型与流体域模型如图3所示。如图4所示，导流器叶根焊缝发生了失效。

表1 主要设计参数

表2 材料特性

图2 鲁尔泵叶轮与导流器三维模型

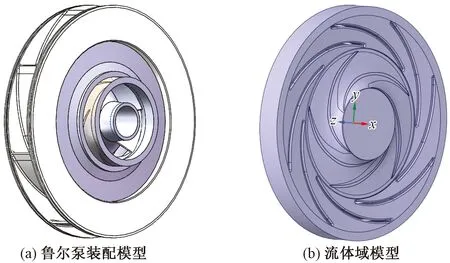
图3 鲁尔泵装配模型与流体域模型

图4 鲁尔泵导流器焊缝失效细节

1.3 流场网格划分

综合考虑ZLM鲁尔泵导流器结构特点以及现场工况，高级尺寸函数选择曲率控制函数(curvature)，其中关联中心(relevance center)设为Fine。

如图5所示，鲁尔泵叶轮部分，最大面尺寸设为10 mm，其他选项保持默认，网格节点数目(nodes)为247 694，网格数目(elements)为1 333 958。网格划分方法选择自动(automatic)。在导流器部分，使用面尺寸控制，网格尺寸设置为0.02，将叶片附近网格精细划分，以提高鲁尔泵流场仿真分析的准确性，为了进行网格质量的监测，其网格正交质量(orthogonal quality)，平均值为0.84，网格质量满足ANSYS Fluent计算要求。网格节点数目为583 093，网格数目为2 962 620。

图5 鲁尔泵网格划分

1.4 流场边界条件设置

根据实际工况与现场调研数据，叶轮设定X轴为旋转中心，转速设定为2 980 r/min，导流器固定在其外侧。叶轮的入口边界设为压力入口，入口压力设为0，叶轮出口与导流器入口设立交界面，导流器出口设定为质量流出口，如图6(a)所示。其余区域设置为壁面。选择液体汽油(gasoil-liquid)作为输送介质，参数保持默认。对于图1所示的模型，采用其中间截面为基准截面用来内流场分析如图6(b)所示。分别设置质量流入口条件不同的5个流量(标准流量1.0Q、0.2Q、0.6Q、1.2Q、1.4Q，Q=2 871 m3/h)进行模拟，用以得出鲁尔泵的水力特性。

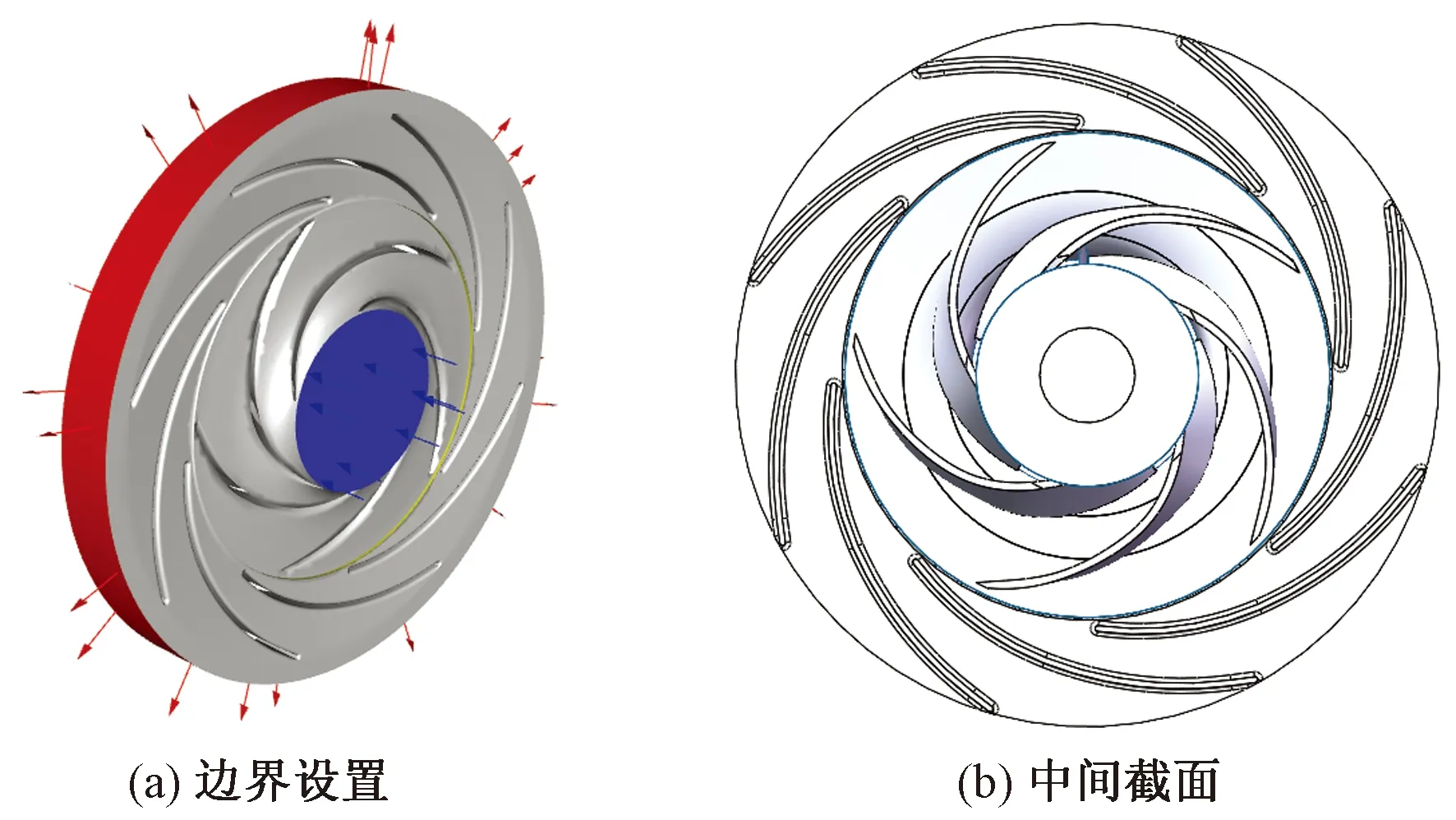
图6 鲁尔泵边界条件设置

1.5 流场求解方法及收敛判据

使用Fluent进行鲁尔泵流场分析时，选择基于压力的求解器，采用伪瞬态模型，在y方向上设置重力加速度值为9.8 m/s2。采用SSTk-ε模型和scalable wall functions壁面函数。选择Coupled方案，梯度为基于最小二乘法的单元，压力二阶，动量二阶迎风，湍动能和湍流耗散率均为二阶迎风。

流场数值计算使用迭代方法求解会产生残差，设置收敛的残差标准10-4，但是为了更加准确判断收敛，运用以下两种方法综合来判断[14]：①监测迭代出的残差值。设置收敛的残差标准为10-4，当迭代出的残差小于这个值时，就可以初步判定计算收敛；②监测导流器出口的总压力。当导流器出口压力恒定不变或是变化量极小时，这时就可以确定计算已经收敛。

2 ZLM鲁尔泵流场特性分析

图7为不同流量下鲁尔泵的静压分布云图，可以看出，同一工况下，在流道入口处静压较小，由于叶轮对流体做功，静压值从从叶轮进口到出口不断上升，在叶轮出口处达到最大值。在同一半径处叶片工作面上，叶片表面静压明显高于其背面静压，并且在叶片出口存在尾迹。随着流量的提升，还可以发现鲁尔泵的静压分布更加均匀，尤其是导流器中的静压值明显下降。

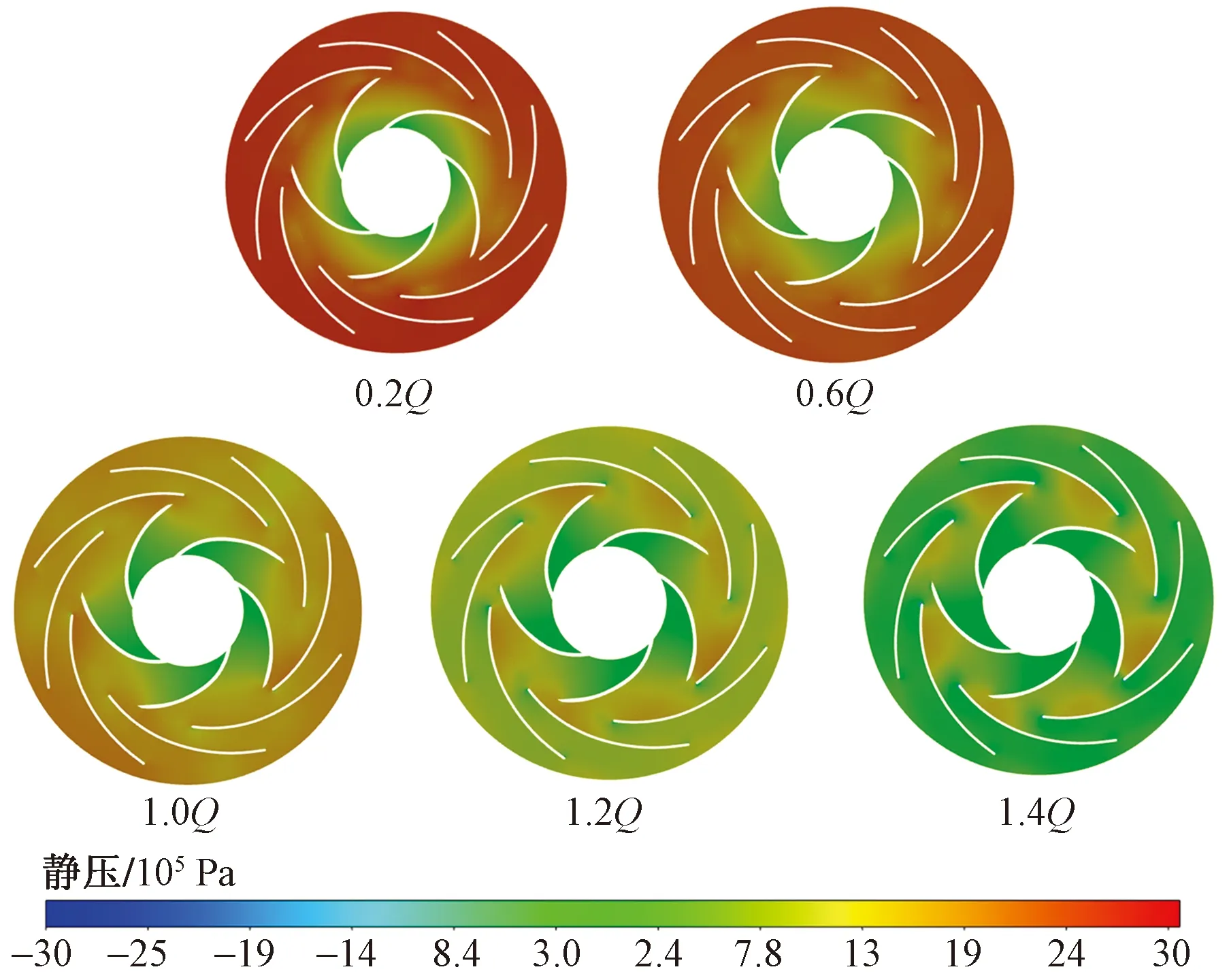
图7 不同工况下鲁尔泵静压分布云图

如图8(1.0Q工况静压分布云图)所示，在导流器叶片根部背面出现了明显的低压区，并且随着流量的提升愈加明显，这种现象是由于高速流体经过导流器叶片时，叶片表面与背面流体分布不均、局部流速过大造成的[15]。而鲁尔泵导流器的叶片与基体采用焊接的方式，这些叶片根部的低压区存在影响此处的焊缝更加容易发生疲劳失效。需要优化导流器的结构设计来减少这一现象的影响来提高鲁尔泵的使用寿命。

图8 1.0Q工况时导流器低压区

图9为鲁尔泵的绝对速度分布云图，可以看出，石油在中间截面的绝对速度分布层次清晰，每个流量点都存在的普遍规律是：在叶轮中，流速随叶片方向逐渐升高，在叶轮出口位置达到最大速度，接着经过导流器的整流作用，速度下降。叶轮中的叶片工作面与背面速度分布大致相同，在导流器当中，同一半径中叶片表面流速明显大于背面流速。

图9 不同工况下鲁尔泵绝对速度分布云图

在小流量工况下(如0.2Q)，叶轮区域绝对流速分布紊乱并且导流器流道中流速分布也较为紊乱，但随着流量提升(1.0Q以上)，可以发现鲁尔泵整体流道流速趋于均匀。

泵叶轮、导流器速度分布总体来说比较均匀，符合离心泵流场的速度分布规律。但在极端工况下(0.2Q)，叶轮出口与导流器入口处速度分布出现较大梯度，会造成较大的水力损失。

从以上的仿真结果(图7～图9)可以发现，导流器叶片根部流场规律使其相比其他地方更易失效，鲁尔泵导流器的焊缝缺陷如图9所示。输送液体经过叶轮的加速，源源不断地快速冲击导流器入口段的叶片，而导流器叶片入口段由于其弧线的结构设计，流体在经过时会被分成两部分，其中叶片背面流速更快，这也导致了局部的低压区域的形成，而鲁尔泵的工作状态会使其内部的流体流速、流量发生一定程度的波动，这些变化让叶片根部处于不断承受交变应力，鲁尔泵导流器的叶片与基体采用焊接的方式，所以这些叶片根部的低压区会加速此处焊缝的疲劳失效。

由于导流器叶片与基体相连接的角焊缝为单侧焊接结构，叶片工作面和背面部分区域有未焊接区域(图10)。所以叶片根部存在一定应力集中，角焊缝内圈一端承受交变的工作应力大，是疲劳裂纹萌生的原因。针对这个问题，可以采用两端面开坡口，叶片两边焊接的方式，且焊角由3 mm增高至4 mm。条件允许的情况下，提高零件的表面质量，特别是在应力集中的叶片根部的表面加工质量，还需要提高焊接质量，尽量减少初始裂纹的产生。通过这些方式可以在不改变导流器结构参数的条件下延长其使用寿命。

图10 叶片未焊接区域

3 ZLM鲁尔泵水力性能分析

图11为鲁尔泵的相对速度分布迹线图，可以看出，鲁尔泵在运行时，叶轮的中间流道处出现了不太规则的流动漩涡。流体进入导流器，经过叶片的整流作用，流体速度迅速下降，导叶截面内在各工况下均出现较大速度梯度，这将增加导流器内的涡流和碰撞损失[16]。不稳定的漩涡是水力效率损失大的原因，这解释了低流量时水力损失较大的现象。

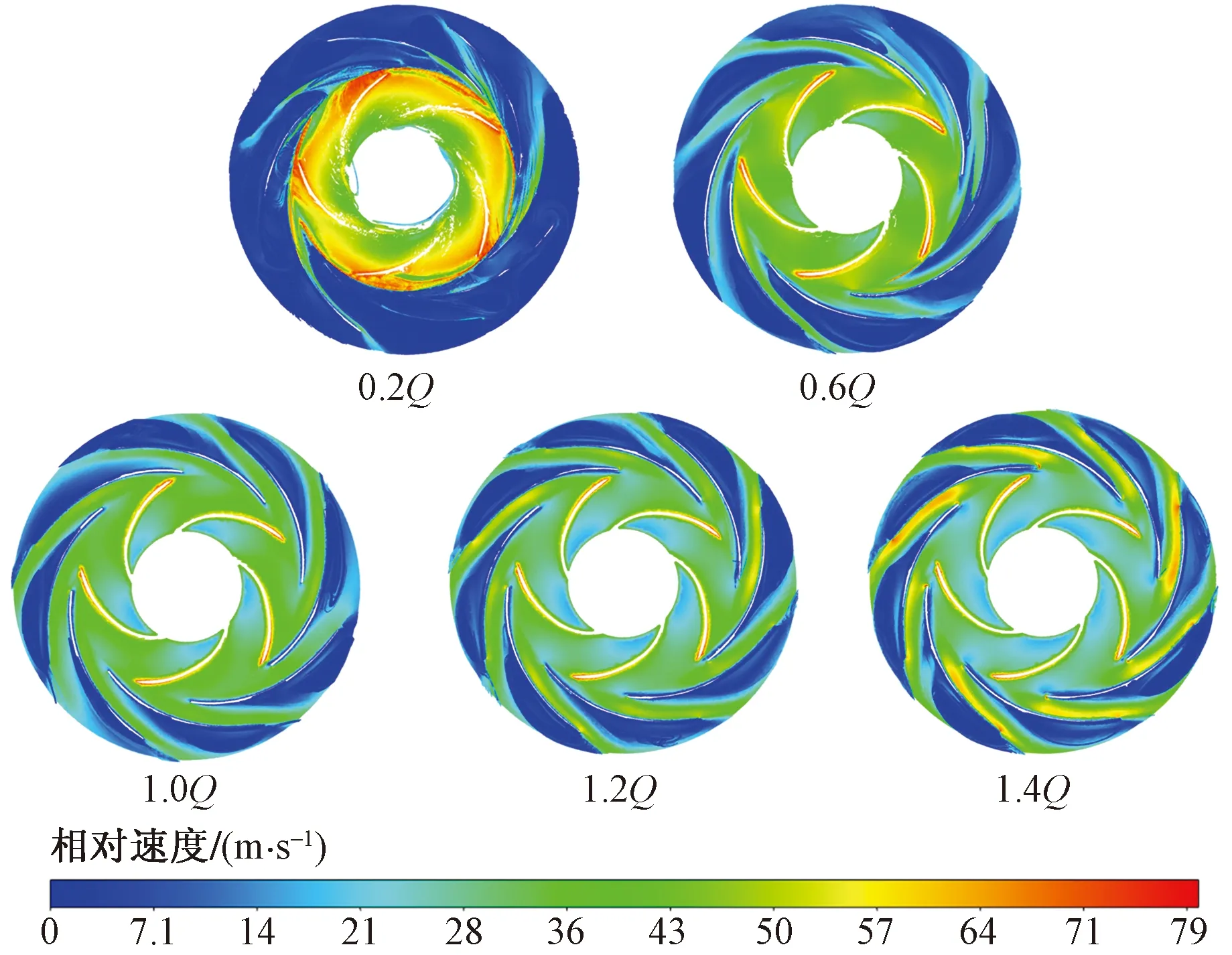
图11 鲁尔泵液相迹线分布图

如图12所示，漩涡的产生在小流量工况中(0.2Q)最为明显，随着提高流量(如1.0Q)，漩涡的区域有所减少，流体相对速度梯度减小，但导流器扩散段内的漩涡区依旧存在。并且流量的增加使得流体速度有一定提高，低流速的区域有一定程度减少。并且因为叶轮和导叶之间存在动静干涉，鲁尔泵在各个工况下运行时，最大速度梯度均在叶轮出口与导叶进口处出现。

图12 鲁尔泵局部迹线图

在极端小流量工况下(如0.2Q)，可以得知其涡流现象非常严重，叶轮出口处速度梯度较大，产生的碰撞损失与水力损失最为严重，在实际使用中，应当避免在较小流量工况下运行。

扬程是指水泵能够扬水的高度。水力效率η指的是水泵的有效功率和轴功率P的比值，高效率的泵做功时所消耗的能源低，水力损失较小，这两个参数是评价泵好坏的关键参数,计算公式分别为

(5)

(6)

式中：P为轴功率；T为扭矩；n为工作转速；Q为流量；H为扬程；η为水力效率。

从表3可以看出，随着流量的增加，鲁尔泵的扬程在不断下降，水力效率先上升后下降，根据大量实验后，得出了鲁尔泵的性能曲线，即Q-H曲线(图13)与Q-η曲线(图14)，该图符合离心泵的一般规律，并且得出在Q=2 871 m3/h是该型号泵的最优工作流量。

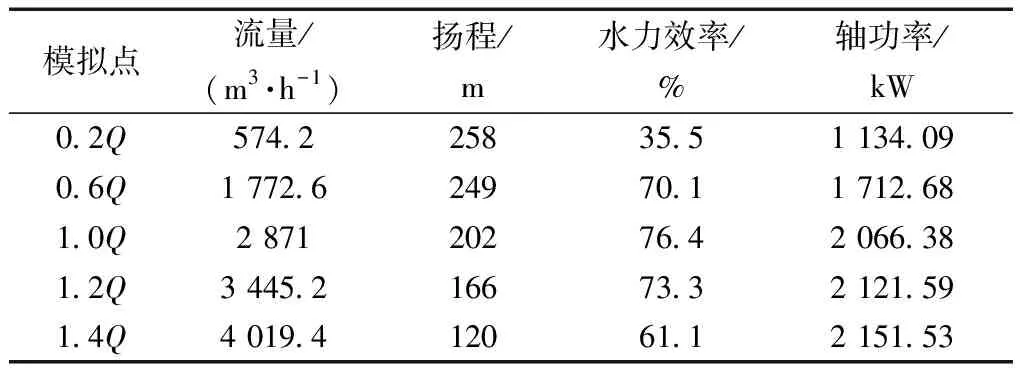
表3 鲁尔泵水力特性模拟结果

图13 鲁尔泵Q-H曲线

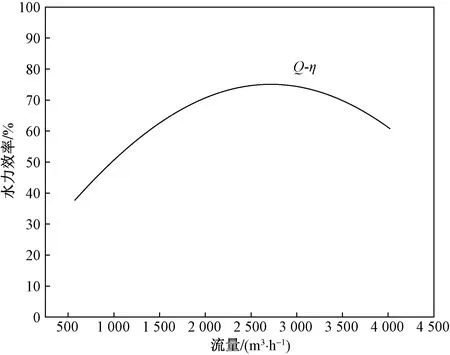
图14 鲁尔泵Q-η曲线

4 结论

(1)鲁尔泵内叶轮静压呈现从中心随叶片方向不断增大的趋势，在叶轮出口达到最大值，而导流器流道静压分布较为均匀，叶片表面静压大于背面静压，并且在叶片根部存在低压区，如果要使流道更加平缓并延长鲁尔泵的使用寿命，叶片建议采用两端面开坡口，两边焊接的方式，焊角由3 mm增高至4 mm，并且尽量提高叶片的表面质量。

(2)鲁尔泵内流体绝对速度从叶轮中心开始，不断提升，在叶轮出口达到最大值，经导流器整流，逐渐趋于均匀。在低流量工况时，叶轮中速度梯度过大，会造成非常大的冲击损失。在实际工作中，应尽量避免在较低工况下运行。

(3)鲁尔泵叶轮内流体的相对速度随着流量的提升，分布趋于均匀，导流器中的不规则漩涡区有所减少，但在超过Q=2 871 m3/h后，导流器中出现了明显的高速低压区，造成了水力损失。在实际工作中，工作流量的设置不应过度偏移标准流量，从而保证产品的寿命与可靠性。