基于Apriori和GP-XGBoost的特高拱坝变形缺失数据填补方法

吴诚姝， 陈 波， 刘庭赫,3

(1.河海大学 水利水电学院， 江苏 南京 210098； 2.河海大学 水文水资源与水利工程科学国家重点实验室， 江苏 南京 210098； 3.中水东北勘测设计研究有限责任公司， 吉林 长春 130021)

1 研究背景

特高拱坝与近坝库岸山体构成一个巨型开放系统，超高的坝高、超大的库容、复杂的地质条件及恶劣的服役环境给工程安全保障带来极大挑战，因而对大坝运行进行实时安全监测与评价尤为重要。随着监测技术水平的日益提高，目前评定大坝运行状态的方法主要是采用埋设原位监测仪器获取能够表征大坝实时运行性态的监测数据，再通过数据处理和分析对大坝的运行状态作出评价。然而，由于监测数据量庞大，且受仪器本身及外界因素影响，监测信息中往往存在数据缺失的现象，会削弱监测数据的有效性，并对后期的数据分析工作带来困难。因此，以合理的方式从海量原始监测数据中集中挖掘潜在有意义的规律和模式，利用大数据技术完成对缺失数据的处理，能够为实际工程提供有价值的决策参考[1-2]。

国内外学者针对缺失数据的填补方法做了相应研究，大致分为插值填补、回归填补、机器学习填补等几个方面。部分学者依据数据集在时间序列上的相关性取得了一些成果，如Song等[3]分别采用插值填补、时间序列统计方法、RNN和LSTM神经网络算法对缺失数据进行了填补，结果表明LSTM神经网络在填补长时间缺失数据方面有较大优势；李正欣等[4]基于多元时间序列变量间的相关性进行了联合数据填补，该方法具有较高的填补精度和抗干扰能力；王一蓉等[5]利用遗传优化算法获取最优的数据参数，如均值、方差等，在此基础上利用马尔科夫链蒙特卡罗法对缺失数据进行填补，有效提高了缺失数据填补的准确度。然而，上述缺失数据的填补方法仅从时间序列角度进行了相关分析，而未结合测点空间位置的邻近特性，尚存在一定缺陷。研究表明，通过空间数据挖掘技术可以寻找数据中隐藏的规律特征，如邱德俊等[6]考虑大坝各测点的空间邻近关系，利用极限学习机拟合了缺失数值；Xu等[7]基于FCM聚类算法提出了实时更新隶属度矩阵的OCS-FCM水质监测缺失数据还原方法，结果表明该方法适用于缺失率大和多属性的数据集；郑霞忠等[8]利用关联规则识别出大坝变形监测数据中的强关联序列并结合DBSCAN聚类算法识别异常点，通过对比强关联序列来甄别由环境突变引起的异常值。有学者将空间数据挖掘技术引入到大坝安全监测领域内，发现了许多能够对工程安全运行决策起关键作用的因素，如利用关联规则研究工程运行影响因子的贡献程度[9-11]，利用聚类算法研究大坝运行的时空特性等[12-14]。

基于上述缺失数据填补的研究现状，传统的依靠人工方法或统计学方法对大坝监测信息预处理在效率和精度方面均难以满足要求，而采用人工智能算法进行缺失数据填补仅考虑时间序列的相关性，在精度上具有一定的局限。据此，本文综合考虑特高拱坝监测信息的时空特性，首先利用Apriori空间关联规则挖掘各测点间的同步性，对测点数据的相关性进行分析，然后根据大坝各测点间监测数据的空间强关联信息，采用优化的XGBoost(extreme gradient boosting)回归模型进行目标测点的缺失测值填补。提出了从时间与空间维度融合关联规则挖掘和人工智能算法方面研究监测信息缺失的处理方法，有效提高了监测数据的可靠性和完整性，以期为特高拱坝服役性态分析做好基础性工作。

2 基于关联分析的监测信息空间挖掘

2.1 关联规则定义

假设存在数据集D={t1,t2,…,tk,…,tn}，tk={i1,i2,…,im,…,ip}，tk(k=1,2,…,n)称为事务，im(m=1,2,…,p)称为项。设I={i1,i2,…,im}为D中全体项组成的集合，则I的任何子集称为D中的项集。若X、Y为D中的两个项集，且X∩Y=Ø，蕴涵式X⟹Y成为关联规则，X、Y分别称为X⟹Y的前项和后项[15]。关联规则常用的基本概念如表1所示。

表1 关联规则中常见的基本概念

2.2 Apriori算法原理

Apriori 算法是使用频繁项集的先验知识从而生成关联规则的经典算法，该算法采用自底向上的遍历思想，主要使用逐层搜索的迭代方法挖掘大数据中潜在的事物联系，以确保关联规则的准确性[16]。为提高算法效率，Apriori算法利用了一个重要性质，即频繁项集的任一子集均为频繁项集。利用该性质可有效缩小频繁项集的搜索空间[17]。

该算法建立关联规则主要包含两个步骤，一是通过迭代搜索事务集D中全部的频繁项集，非频繁项集在迭代过程中被剪枝剔除，直至不能搜索到任何频繁k项集为止；二是比较频繁项集间的最小置信度以建立强关联规则。该算法的主要流程如图1所示。

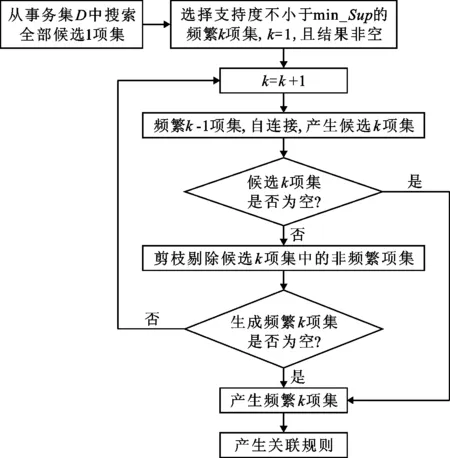
图1 基于Apriori算法的关联挖掘流程图

2.3 基于Apriori算法的大坝监测信息空间关联挖掘

为了评定大坝各测点监测信息的相关性，采用Apriori算法开展多测点空间关联挖掘，其流程如图2所示。

结合图2将大坝监测信息空间关联挖掘的主要步骤介绍如下：

(1)设定前、后项。关联挖掘的对象主要是空间上位于不同位置的两个测点，同一时间截面内两个测点具有不同的监测效应量，因此将两个测点的监测效应量分别作为前项和后项，前项X表征某测点在t时刻的监测效应量信息，后项Y表征另一个测点在t时刻的监测效应量信息。

(2)划分数据属性。由于大坝监测数据是连续的测值，难以反映定性的信息，因此在关联分析前，需要根据测值的特征将其归属于不同的属性区间，这里结合监测数据的相似性特征，以测值的大小和增量作为衡量测值相似性的指标，按照测值的大小和增量划分属性区间如下：

假设大坝监测数据存在T个时间截面的测值，将测值特征数据集记为DT，按照等距分箱的思想，结合特征数据集中的最大值DT max和最小值DT min将数据集DT等距分为3个属性区间，即：

d=(DT max-DT min)/3

(1)

(2)

由此生成测值特征的属性区间包括[a1,a2)、[a2,a3)、[a3,a4]。

(3)设定阈值。为了评定测点间的整体关联性，在支持度的基础上提出测点同步支持度的概念，定义如下：

假设存在测点δ1,δ2,…,δn，共T个时间截面的监测数据，经步骤(2)转换某一时间截面t的项集集合记为xi(i=1, 2,…,n)，则n个测点的同步支持度为：

(3)

通过同步支持度可以定量评定不同测点之间时空数据的相似性，在关联挖掘时需要设定最小同步支持度和最小置信度作为强关联测点的筛选条件。

(4)挖掘强关联测点。最后当测点间满足设定的同步支持度和置信度阈值时，输出强关联测点；否则认为测点关联性较弱，予以删除。

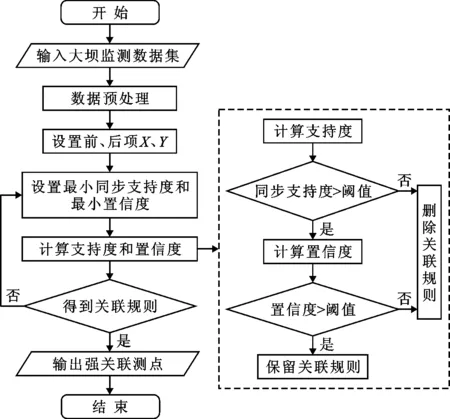
图2 大坝监测信息空间关联挖掘流程图

3 基于GP-XGBoost的监测信息空缺填补

3.1 基于关联测点的测值残缺填补

如图3所示，假设某混凝土拱坝上存在测点①、②、③，测点②存在残缺信息，经关联分析后建立了测点①→②，测点③→②的强关联规则，即考虑采用测点①、③对测点②的空缺数据进行填补，将测点②的监测序列表示为测点①和测点③的函数如下：

δ2=g(δ1)+g(δ3)+ε0

(4)

式中：g为测点①和测点③关于测点②的效应量函数；ε0为用测点①和测点③拟合测点②的残差。

传统的基于空间近邻的数据缺失填补方法仅考虑了测点的空间位置，未从测值本身特征去分析各测点间的相关性，且从空间位置上来看，缺失测值的目标测点附近布置了多个测点，很难评定选用哪些测点填补数据最为合适[18]。为解决这个问题，本文首先对目标测点的邻近测点监测效应量进行关联分析，然后按照与目标测点的同步支持度进行排序，最后优先选取关联度高的测点对目标测点进行填补。为了进一步提高填补精度，采用贝叶斯优化的XGBoost模型对缺失值进行填补。

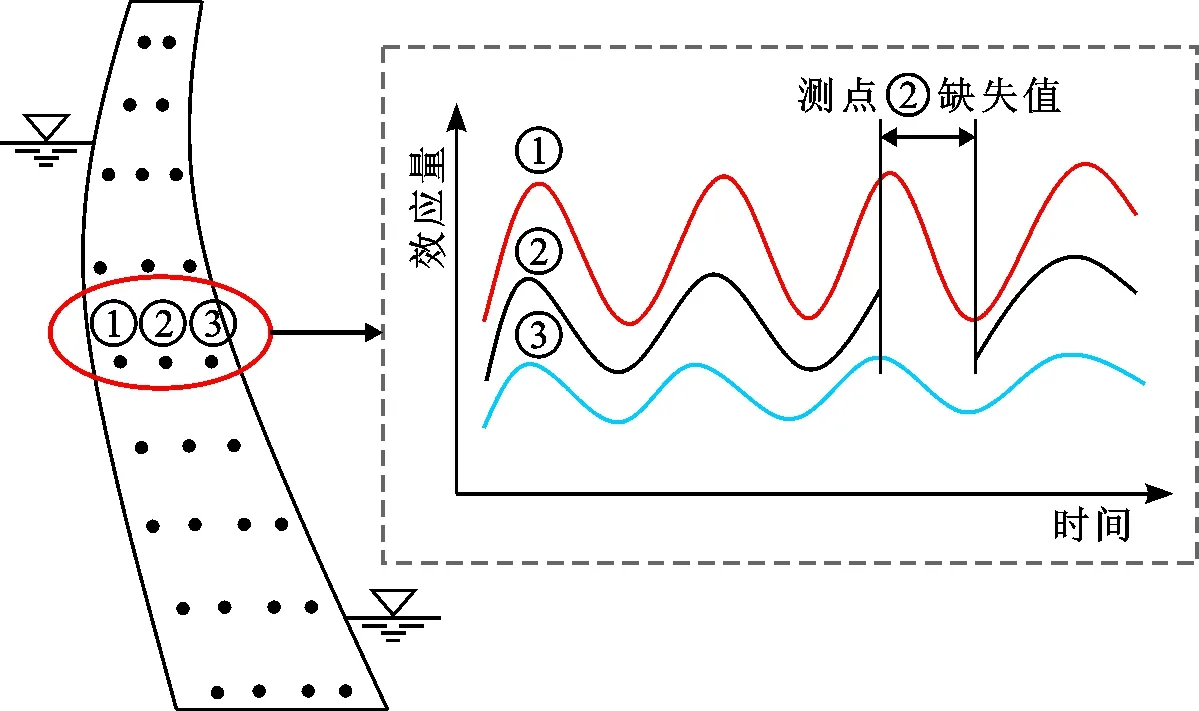
图3 基于关联测点的测值残缺填补方法示意图

3.2 GP-XGBoost算法原理

XGBoost算法是由传统梯度提升树算法(gradient boosting decision tree，GBDT)发展而来，相比于GBDT算法，XGBoost算法对损失函数加以改进，支持并行计算，大幅提高了算法效率[19-20]。

本文主要利用XGBoost算法高效、精准的回归预测能力结合强关联测点的已知信息对目标测点的未知信息进行填补。XGBoost算法的核心思想是多个基础模型的线性组合[21]，对于一棵含t个基础模型的集成树来说，可表示为：

(5)

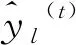
构建目标函数如下：

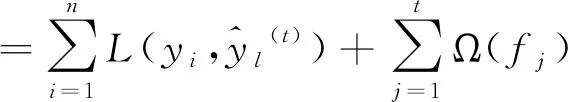
(6)

其中，Ω(fj)为正则项，可表示为：

(7)

式中：γ和λ为正则化系数；T为叶子节点的个数；ω为叶子节点的权重。

对函数式(6)中损失函数L作二阶泰勒展开：

f(x+Δx)≈f(x)+f(x)′Δx+f(x)″Δx2

(8)

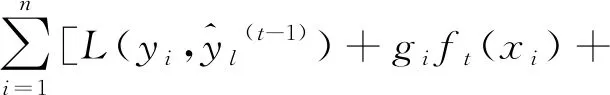
(9)

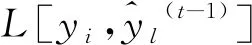
gi和hi可以表示为：

(10)

通过迭代找到使目标函数最大化降低的ft，即完成模型的训练过程。

为了进一步提高XGBoost模型的精度，本文结合基于高斯过程(Gaussian Process, GP)的贝叶斯优化算法优化XGBoost模型的重要参数，以确定最佳的回归模型。贝叶斯优化框架是一个迭代的过程，主要通过采集函数选择下一个最佳评估点xt并计算目标函数值yt，更新历史观测集和概率代理模型，以此不断循环得到最优解[22-23]。贝叶斯优化框架最核心的两部分是概率代理模型和采集函数，概率代理模型用于代理目标函数，其中迭代速度快、扩展性高的高斯过程应用较为广泛，考虑到大坝监测数据集庞大，以高斯过程作为优化内核可以明显提高效率[24]；采集函数由后验概率分布决定，作用是选择下一个潜力最高的评估数据。以下详细介绍概率代理模型(高斯过程)和采集函数具体内容：

(1)高斯过程。在以高斯过程作为内核进行参数优化时，认为目标函数f(x)满足GP过程，构成如下：

f(x)～GP(E(f(x)),k(x,x′))

(11)

式中：E(x)为期望，通常取值为0；k(x,x′)为x的协方差。

假设一个满足均值为0的先验分布p(f|X,θ)：

p(f|X,θ)=N(0,∑)

(12)

式中：X为训练集{x1,x2,…,xt}；f为目标函数值集合{f(x1),f(x2),…,f(xt)}； ∑为k(x,x′)构成的协方差矩阵(∑i,j=k(xi,xj))；θ为超参数。

考虑存在满足相同高斯分布的观测噪声ε，得到似然分布：

p(ε)=N(0,σ2)

(13)

P(y|f)=N(f,σ2I)

(14)

式中：y为观测值集合{y1,y2,…,yt}。

进一步地，结合公式(12)和(14)，可以得到边际似然分布：

=N(0,∑+σ2I)

(15)

根据高斯过程，存在如下联合分布：

(16)

K*T={k(x1,X*),k(x2,X*),…,k(xt,X*)}

(17)

K**=k(X*,X*)

(18)

式中：f*为函数预测值；X*为输入值。

根据公式(16)，得到预测分布如下 ：

p(f*|X,y,X*)=N(, Cov(f*))

(19)

=K*T[∑+σ2I]-1y

(20)

Cov(f*)=K**-K*T[∑+σ2I]-1K*

(21)

式中： 为预测均值； Cov(f*)为预测协方差。

(2)采集函数。采集函数作为评估潜力参数的重要依据，通常优化目标便是在全集参数A中寻找f(x)达到极值时的X集合，其表达式如下：

x*=arg maxx∈Af(x)

(22)

为了对贝叶斯参数优化过程中的模型精度进行定量评价，本文以K-折交叉验证产生的均方误差MSE作为训练过程中模型精度的评价指标。

假设通过关联分析得到目标测点δn+1的n个强关联测点δ1,δ2,…,δn，将n个强关联测点的测值作为输入，目标测点δn+1的测值作为输出，则建立的GP-XGBoost算法的训练优化过程如图4所示。

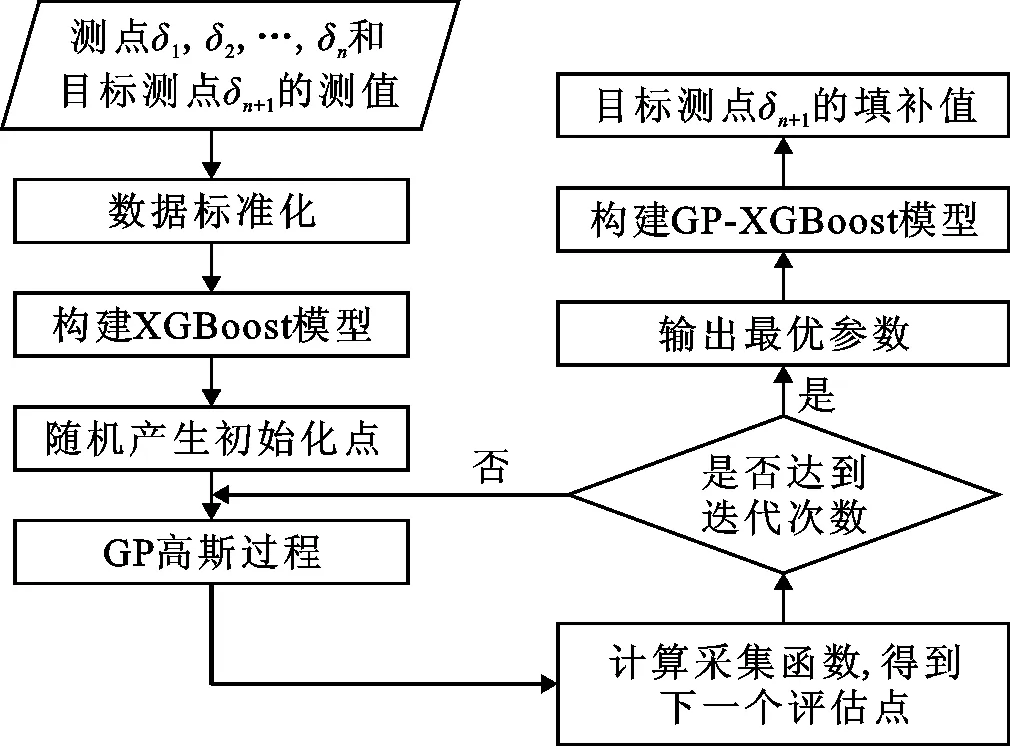
图4 GP-XGBoost算法的训练优化流程图

4 工程实例

锦屏一级水电站特高拱坝地处深山峡谷河段，坝基高程为1 580.00 m，最大坝高为305.00 m，正常蓄水位为1 880.00 m，属于大(1)型工程。该工程目前处于稳定运行阶段，为了监测坝体变形，分别在5#、9#、11#、13#、16#和19#坝段不同高程布置垂线测点，如图5所示，收集了该特高拱坝近5年的水平径向位移监测数据进行研究。

4.1 测点变形序列关联分析

基于Apriori算法进行测点序列的关联分析时，首先从空间位置上选取与目标测点位置相邻的多个测点，即以目标测点为中心，关联分析窗口取目标测点相邻的8个测点(图6)，分别计算与中心目标测点的关联程度。首先将变形数据从定量测值转换为定性属性，考虑用变形测值大小和增量衡量测点变形序列的关联程度，按照测值大小划分为A、B、C 3个属性区间，分别表示变形较大、变形一般和变形较小；又按照增量情况划分为a、b、c 3个属性区间，分别表示变形相对上一时刻增大、不变和减小，在此基础上展开关联挖掘工作。

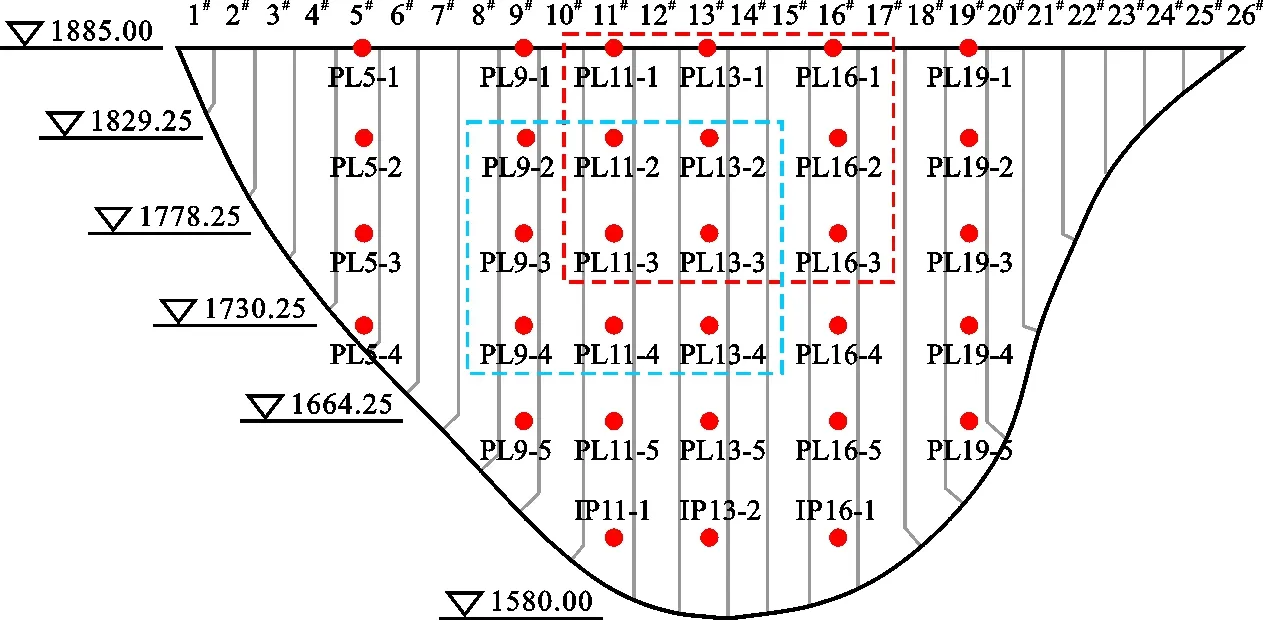
图6 关联分析测点选取窗口示意图(高程单位：m)

以PL11-3测点作为目标测点，选取2016年1月至2021年3月共1 791组水平径向位移监测数据，分别与其空间相邻测点PL9-2、PL9-3、PL9- 4、PL11-2、PL11-4、PL13-2、PL13-3、PL13- 4进行关联分析，计算结果如表2、图7所示。结果表明，当设置最小同步支持度为85%时，与PL11-3测点强关联测点为PL11-2、PL9-3、PL13-3和PL11-4；当设置最小同步支持度为90%时，强关联测点为PL11-4。

为了进一步验证强关联测点的可信度，计算最小同步支持度为85%时的置信度，设置最小置信度为80%，表3为PL11-3测点与强关联测点置信度计算表。由表3可见，PL11-4和PL13-3测点满足置信度要求，PL11-2和PL9-3测点在属性集Ba区间与目标测点PL11-3的关联规则略小于最小置信度，但考虑到这两个测点出现在Ba属性集所占的比例较低，因此保留这两个强关联测点，用于填补目标测点PL11-3的残缺数据。

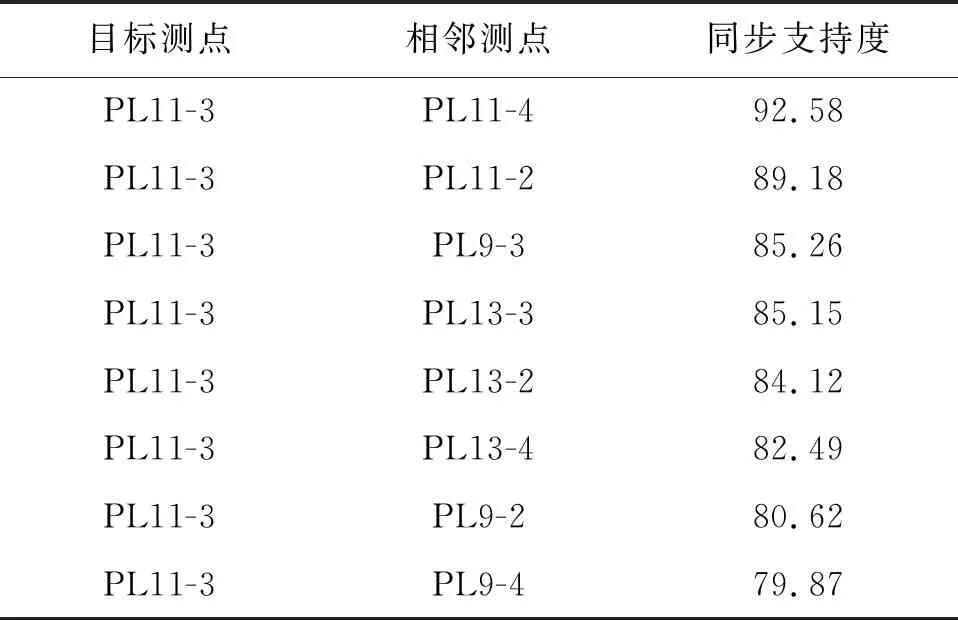
表2 各测点关联同步支持度计算表 %

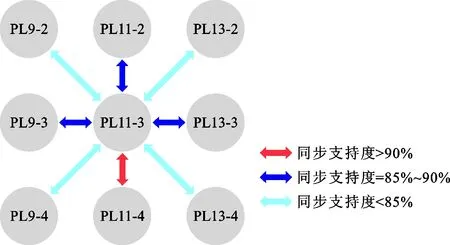
图7 基于Apriori算法的关联挖掘结果示意图

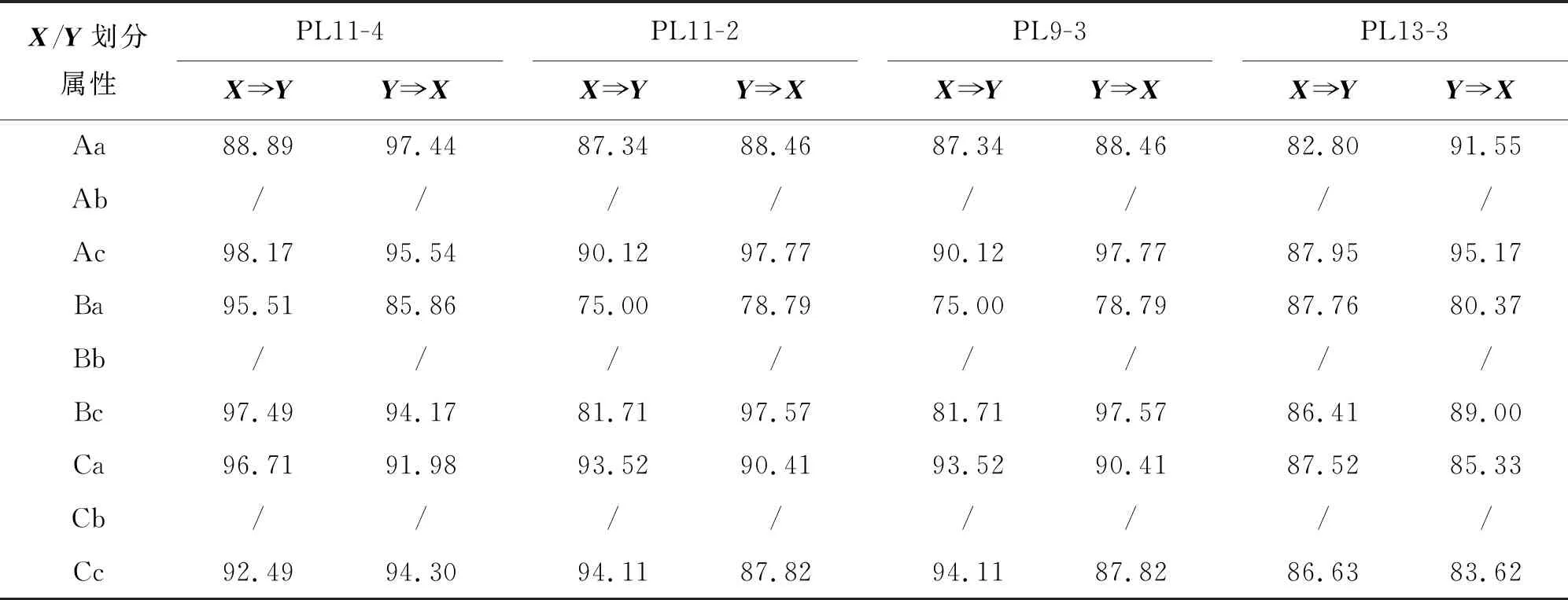
表3 PL11-3测点与强关联测点置信度计算表 %

4.2 GP-XGBoost模型对缺失值的填补结果

目标测点PL11-3存在部分连续的残缺信息，为了验证本文提出数据填补方法的有效性，首先假定该测点在2020年12月20日测点数据丢失，测值为42.540，其他关联测点数据集较完整。基于上述关联分析的结果，按照与目标测点PL11-3关联度从高到低的顺序，依次选取不同数量的测点变形序列作为XGBoost模型的输入样本，输出为目标测点PL11-3除缺失数据以外的完整数据，建立XGBoost模型进行训练，再采用训练好的模型对PL11-3测点缺失数据进行填补。

XGBoost模型基于python平台进行构建，主要参数max_depth(基模型包含最大深度)和n_estimators(基模型数量)对XGBoost模型的回归精度起着关键作用，故采用贝叶斯优化，迭代100次，图8(a)、8(b)分别为贝叶斯优化和随机搜索过程中均方误差MSE的变化曲线。由图8可见，贝叶斯优化每次迭代过程的MSE均较小，具有主动寻优的能力，而随机搜索由于参数的随机组合会出现局部MSE较大的情况。贝叶斯优化在迭代23次后MSE达到最小，为7.64×10-6mm2，而随机搜索在迭代68次后MSE才达到最小，为2.60×10-5mm2。因此，贝叶斯优化采用贝叶斯优化参数能够高效寻优，具有良好的表现。

基于4.1节关联分析的结果，按照与目标测点PL11-3关联程度由高到低的顺序选取不同的学习样本对其缺失值进行填补，XGBoost参数由贝叶斯优化，结果如表4所示。

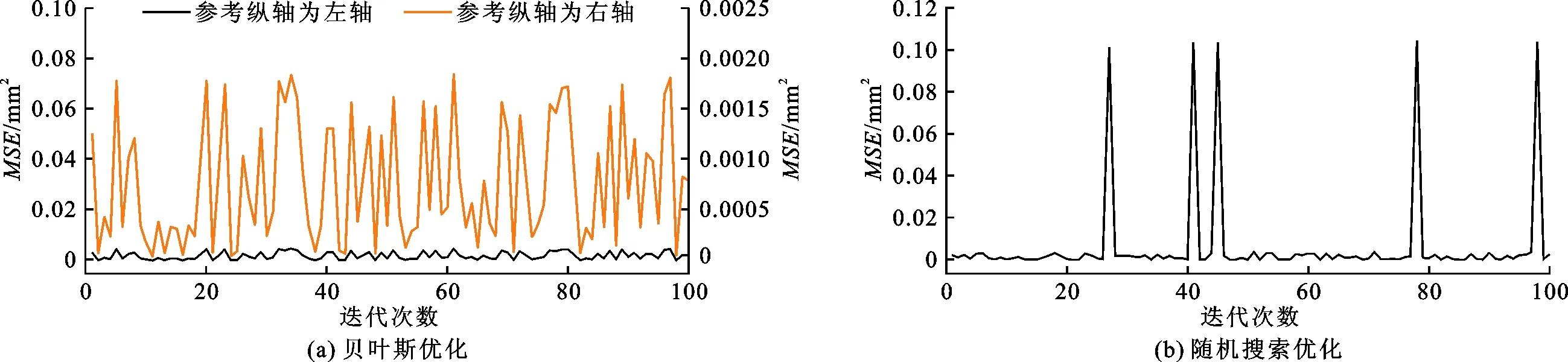
图8 贝叶斯优化和随机搜索过程中MSE的变化曲线

表4 不同学习样本对目标测点PL11-3缺失数据的填补结果

由表4可见，当采用强关联测点PL11-2、PL11-4作为学习样本时，填补值与缺失值(42.540)最为接近，即精度最高。除此以外，采用其他的强关联测点作为填补测点时，也能够取得较好的填补结果，如{PL11-2、PL11-4、PL9-3}、{PL11-2、PL11-4、PL9-3、PL13-3}等。值得注意的是，当学习样本中出现邻近的非关联测点时，会导致模型精度产生不同程度的降低，影响填补值的精度，如当学习样本为与目标测点关联程度最低的PL9-2和PL9-4测点时，模型的估计值为42.820，是估计偏差最大的情况。因此在采用空间邻近关系填补缺失测值之前进行关联挖掘是很有必要的。

表5给出了不同方法对测点PL11-3的数据缺失填补结果比较，可见本文采用的贝叶斯优化XGBoost算法的填补精度要优于传统的插值方法。

表5 采用不同方法对目标测点PL11-3数据缺失的填补结果比较 mm

大坝监测数据中的粗差被剔除后，会出现多个单点空缺，另外，由于监测仪器损坏或环境等因素影响，监测数据中也会存在连续的残缺信息，因此采用本文提出的方法，利用强关联测点PL11-2、PL11-4对目标测点PL11-3存在的多段连续空缺测值进行填补，结果见表6。

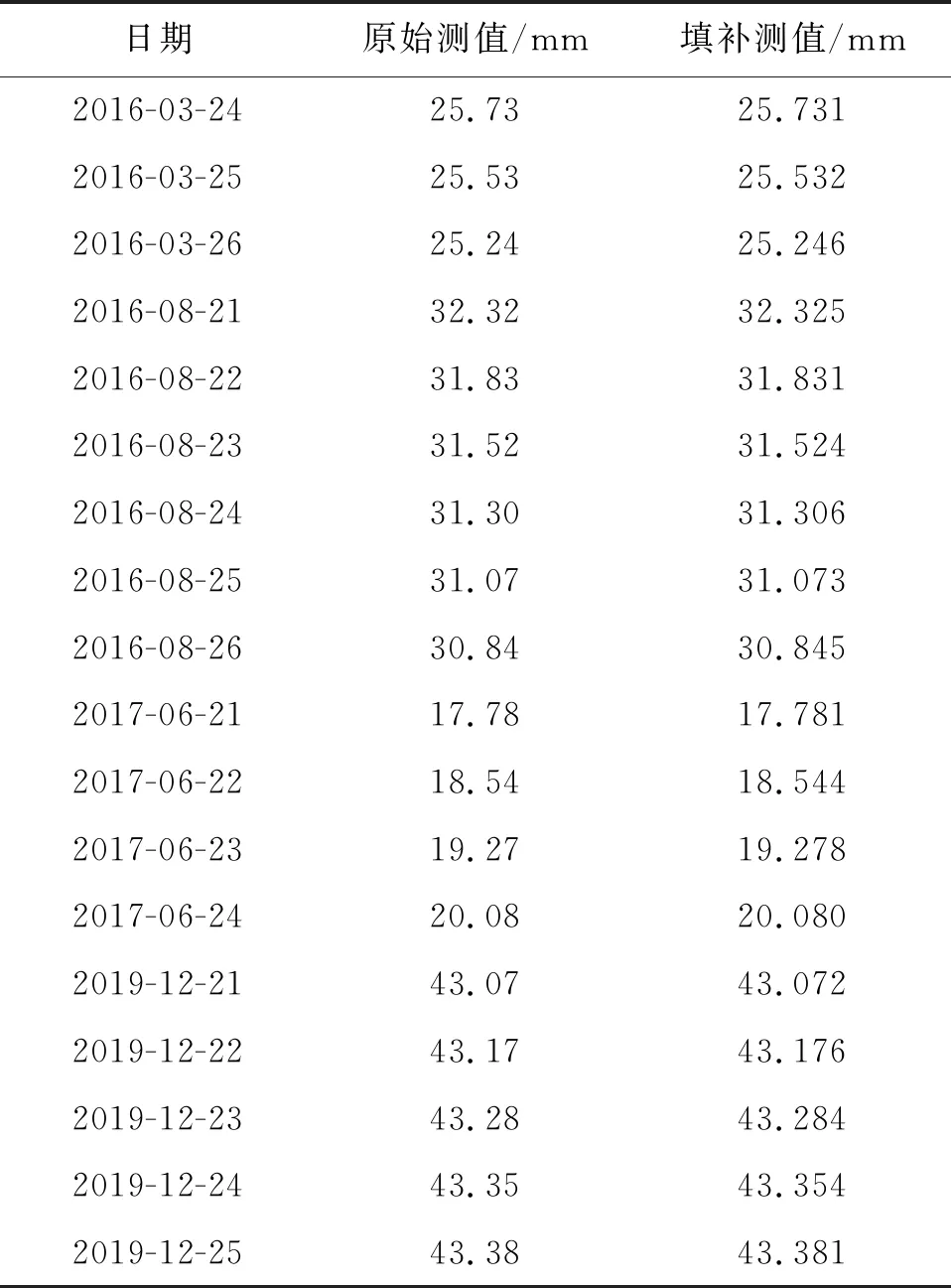
表6 基于GP-XGBoost的测点PL11-3多测值填补结果

5 结 论

针对传统缺失测值填补效率与精度的不足，借助关联挖掘规则，构建了目标测点空间分布的强关联信息，以此为基础利用优化的回归模型进行数据拟合，实现了从时空角度结合关联规则挖掘、机器学习等技术手段对特高拱坝长期变形缺失数据的高效精准填补，为大坝安全监控信息的挖掘、建模及评价工作提供了可靠基础，主要成果如下：

(1)考虑各测点间的空间邻近关系，引进空间关联规则，基于Apriori算法挖掘了目标测点的邻近测点监测效应量在空间维度上的关联性，按照与目标测点的同步支持度排序结果，优选出与目标测点关联度高的测点，获取了测值填补的强关联信息。

(2)结合基于高斯过程的贝叶斯优化算法优化XGBoost模型的重要参数，确定了最佳的回归模型。根据强关联测点的已知信息，利用XGBoost算法高效、精准的回归预测能力对目标测点中的残缺测值进行填补，高精度还原了变形监测数据中的缺失信息，保障了监测信息的完整性与准确性，为后续的分析工作提拱了高质量的数据基础。

(3)以锦屏一级水电站特高拱坝PL11-3测点为例，可得采用强关联测点作为学习样本时，填补值与缺失值最为接近，当学习样本中出现邻近的非关联测点时，会导致模型精度产生不同程度的降低，进而验证了采用空间关联挖掘填补缺失测值的必要性。