基于误差权重的站点降水订正预报方法研究
庄晓宵
修水县气象局, 江西 九江 332400
0 引 言
近年来,因温室效应日益加剧,导致全球气候发生巨大变化。极端灾害性天气频发,对社会发展和人民生活造成严重影响。以位于江西省西北部、修河上游的修水县为例,2017年6月底至8月中旬,出现了三次全区大暴雨天气过程,引发严重洪涝灾害,直接经济损失达11.3亿元。降水精细化预报的迫切需求,与当前基层台站业务能力产生巨大矛盾。然而,因初始条件、地形及物理参数化等因素影响,数值模式不可避免地会产生预报误差。修水县地处幕阜山脉与九岭山脉之间(图1),地形条件复杂,不同区域间海拔高度差可达1—1.5 km,进一步加大了降水精细化预报的难度。当前,基层台站已能调用全球多家数值模式数据,如何快速地进行模式性能分析及海量数据处理,并进一步作出适当的预报订正,是当前基层台站亟待解决的问题。

图1 修水县行政区域(黑色实线)及海拔高度(填色,单位:m;红色三角为修水国家基本气象站,深蓝色实线为修河部分流域)
长期以来,不同学者针对降水订正预报开展了大量研究工作。张蓓等(2019)使用线性回归方法对CMIP5模式进行订正,发现能较好地再现我国降水气候分布特征。池艳珍等(2020)使用线性回归方法对福建前汛期降水预测进行订正,明显提高了BCC_CSM 1.1m模式的预测能力。庄晓宵(2017)基于误差统计量分析、经验正交函数(EOF)分解和功率谱分析等方法对江西北部地区汛期ECMWF模式24 h降水量预报进行误差分析,发现对特征站点设置一定的误差阈值能有效提高模式的预报准确率。以上传统的降水订正预报往往只关注单一数值模式,或仅使用统计学方法对模式历史误差作简单的定性分析,存在一定局限性。
随着信息技术水平不断提高,基于多模式的集成预报研究得到迅速发展(智协飞和赵忱,2020)。代刊等(2016)对多模式暴雨预报检验的研究表明,经最优百分位法订正后,风险评分略优于预报员。吴启树等(2017)、危国飞等(2020)均基于最优风险评分法对多模式进行订正,改进了模式的风险评分。王德立等(2020)使用概率匹配法对台风个例多模式预报进行订正,改善了小雨和特大暴雨的预报能力。智协飞和吕游(2019)利用频率匹配法对多模式降水预报进行客观订正,有效减小了预报误差。基于预报误差的统计学模型,多模式集成预报能有效提高气象要素的预报准确度(智协飞和赵忱,2020)。在多模式集成预报中引入使用滑动训练期的算法,将大幅缩减对历史数据的依赖(包慧濛和李威,2018),同时数据训练期的选取将对计算效率和预报准确率产生较大影响(郝翠等,2019)。若训练期过短或过长,将不利于消除模式的随机误差或系统误差(何珊珊等,2021)。智协飞等(2013)对固定训练期与滑动训练期降水订正效果进行对比,发现滑动训练期可有效提高多数预报时效的降水风险评分。
然而,以上研究基本只关注降水量,未对降水量级进行深入分析,且多为单一的大尺度数值模式之间集成,对于中尺度数值模式的应用较少,而中尺度模式具有较高的分辨率和较完善的物理过程,能改进大尺度模式对局地要素的描述,被广泛应用于极端降水事件研究中(魏培培等,2019)。此外,在订正方案的选取上,以数值模式平均绝对误差为权重的降水订正预报仍为研究空白。为进一步加强基层台站降水订正预报能力,文中以数值模式降水量级预报误差分析为基础,对包含中尺度模式的多种数值模式进行智能筛选,并引入滑动训练期,根据算法生成模式动态权重,最终在订正预报集合中进行概率优选,探索一种适用于基层台站的多模式集成的降水订正预报方法。
1 数据与方法
1.1 数 据
研究使用的实况数据为2018—2020年逐日08—08时(剔除降雪日,共1 076 d)修水国家基本气象站(站号57598)降水实况产品,并处理为对应降水量级。模式数据使用对应日期的欧洲中期天气预报中心预报系统EC(ECWMF,简称“欧洲模式”,分辨率0.125°×0.125°)、美国国家环境预报中心预报系统NC(NCEP,简称“美国模式”,分辨率0.5°×0.5°)、日本气象厅预报系统JP(JMA,简称“日本模式”,分辨率0.5°×0.5°)、中国气象局全球同化预报系统CG(CMA-GFS,简称“全球模式”,分辨率0.25°×0.25°)、中国气象局上海数值预报模式系统CS(CMA-SH9,简称“华东模式”,分辨率0.1°×0.1°)等5种模式降水预报产品。各模式起报时间均为20 h,预报时效为24 h(实际为36 h,下同)及48 h(实际为60 h,下同)。模式降水量使用双线性插值方法投影到站点,并处理为对应降水量级。
1.2 方 法
1.2.1 误差分析
降水量级预报误差E(Error)为降水量级预报量级F(Forecast)与降水量级实况值O(Observation)之间的差值,即
En=Fn-On
(1)
其中,n=1,2,...,N,表示第n次预报,N表示预报样本总量。若En>0,记为正误差;若En<0,则记为负误差。
预报准确率FA(Forecast Accuracy),即预报值与实况值相等的概率。当F=O,即En=0时,记为一次预报准确事件。
平均绝对误差MAE(Mean Absolute Error),表示预报与实况的平均偏离程度,其计算式为

(2)
均方根误差RMSE(Root Mean Squared Error),表示预报误差的离散程度,其计算式为

(3)
1.2.2 检验方法
根据中国气象局《中短期天气预报质量检验办法(试行)》,降水预报使用晴雨准确率(PC)、风险评分(TS)、空报率(FAR)及漏报率(PO)进行检验,其计算式分别为

(4)
ΔPC=PC-PC′
(5)
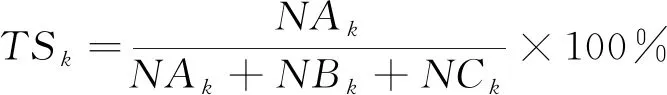
(6)
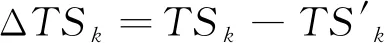
(7)

(8)

(9)
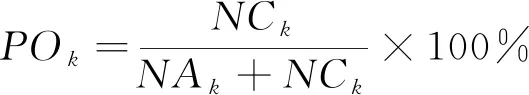
(10)
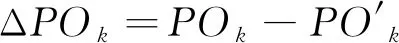
(11)
其中,MA为有降水时预报正确次数;MB表示有降水时空报次数;MC表示有降水时漏报次数;MD表示无降水时预报正确次数;NA表示预报正确次数;NB表示空报次数;NC表示漏报次数;ΔPC、ΔTS、ΔFAR、ΔPO为订正预报相对各模式的晴雨准确率差异值、风险评分差异值、空报率差异值、漏报率差异值,其中风险评分差异值也称为技巧评分。k表示降水量级,文中选取量级为小雨、中雨、大雨、暴雨及以上,分别以1、2、3、12表示。
1.2.3 订正方案
文中使用基于平均绝对误差权重的多模式集成降水订正预报方案。方案中计算了所有初始模式组合顺序(共10种)内待定最优订正预报值,消除了初始模式组合顺序对最终订正预报值可能造成的影响。图2给出了降水订正预报流程。
训练期(p)表示自当前订正预报时刻前移的窗口期,以日数为单位。各入选模式权重(Wi)的计算式为
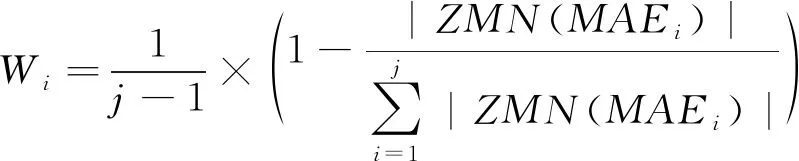
(12)
其中,i=1,2,...,j,表示第i个入选模式;j为入选模式总量;ZMN表示对数据作标准化处理。特殊情况下,若所有入选模式平均绝对误差均为0,则各入选模式权重相同。由此可得订正预报方程:

(13)
其中,Fr表示待定订正预报值,文中其遵循有利于更大量级降水规则向上取整。

图2 降水订正预报流程
2 误差分析
分析2018—2020年模式逐日24 h降水量级预报误差(简称“误差”,下同)(图3左)。各模式正负误差交替出现,无明显规律,且正负误差均值均约为1个量级,表明各模式正负误差均以1个量级为主。模式24 h正误差总体不超过2个量级,其中欧洲模式、美国模式、华东模式最大为4个量级,日本模式最大仅为2个量级;模式24 h负误差总体仍不超过2个量级,其中除华东模式最大为4个量级外,其余模式最大均为3个量级。模式24 h预报准确率范围为59.57%—69.7%,其中较大的为日本模式、华东模式;平均绝对误差范围为0.346—0.478,其中较小的为日本模式、华东模式;均方根误差范围为0.661—0.827,其中较小的为日本模式、欧洲模式。除日本模式外,各模式误差均以正误差为主,美国模式正负误差概率差值为最大,日本模式为最小。分析误差30 d滑动平均值可知,欧洲模式、美国模式、全球模式误差无明显季节变化,四季均易出现正误差,且夏季最为明显;日本模式夏季易出现正误差,其余季节易出现负误差;华东模式冬季易出现负误差,其余季节易出现正误差。由此可见,各模式夏季24 h预报均易出现正误差,可能是由于夏季对流性降水增多,各模式相应增大了预报频次所造成。
分析2018—2020年模式逐日48 h误差(图3右)。各模式正负误差仍交替出现,无明显规律,且正负误差均值均约为1个量级,表明各模式正负误差仍均以1个量级为主。模式48 h正误差总体仍不超过2个量级,其中欧洲模式、美国模式、华东模式最大仍为4个量级,其余模式最大均为3个量级;模式48 h负误差总体仍不超过2个量级,其中华东模式最大为4个量级,美国模式最大仅为2个量级,其余模式最大均为3个量级。模式48 h预报准确率范围为54.93%—66.17%,其中较大的为日本模式、华东模式;平均绝对误差范围为0.420—0.532,其中较小的为华东模式、日本模式;均方根误差范围为0.758—0.868,其中较小的为欧洲模式、日本模式。各模式误差均以正误差为主,美国模式正负误差概率差值仍为最大,日本模式仍为最小。从误差30 d滑动平均可知,欧洲模式、美国模式、全球模式误差无明显季节变化,四季仍均易出现正误差,且夏季最为明显;日本模式春、夏季易出现正误差,其余季节易出现负误差;华东模式冬季易出现负误差,其余季节易出现正误差。由此可见,各模式夏季48 h预报仍均易出现正误差,原因分析与24 h相同。
对比模式24 h及48 h误差可知,各模式24 h预报准确率高于48 h,24 h平均绝对误差及均方根误差均小于48 h,即各模式24 h误差小于48 h;各模式48 h正误差概率相比24 h均有所增大,欧洲模式、华东模式48 h负误差概率相比24 h有所增大,其余模式均有所减小;无论24 h或48 h,华东模式、日本模式误差均较小。
3 检验分析
3.1 晴雨准确率
分析2018—2020年晴雨准确率(图4a、4b)发现,模式24 h晴雨准确率为75.00%—81.97%,其中日本模式、华东模式较高;模式48 h晴雨准确率范围为71.38%—80.48%,其中华东模式、日本模式较高;模式24 h晴雨准确率均高于48 h。相比48h晴雨准确率,24h晴雨准确率提高最大的为全球模式,最小的为华东模式。24 h和48 h晴雨准确率平均最大的为华东模式,最小的为全球模式。

图3 2018—2020年各模式逐日24 h(左)、48 h(右)降水量级预报误差(柱形为误差,虚线为误差均值,黑色实线为误差30 d滑动平均)
3.2 分级检验
对2018—2020年各模式24 h预报进行分级检验,得到各降水量级风险评分、空报率及漏报率(图4c、4e、4g、4i)。各模式风险评分总体随降水量级增大而降低,小雨—大雨风险评分大致相当,暴雨及以上降水风险评分则有较大差异,其中华东模式、欧洲模式、美国模式风险评分较高,其余模式风险评分较低,特别是全球模式风险评分为0。各模式空报率总体随降水量级增大而增大,其中小雨空报率较小,中雨—大雨大致相当,暴雨及以上降水有所增大,特别是全球模式空报率为100%;日本模式空报率随降水量级先增后迅速降低为0,表明其对24 h暴雨及以上降水可能具有一定的预报指示意义。各模式漏报率总体随量级增大而增大,其中全球模式随量级增大最快,暴雨及以上降水漏报率为100%。进一步对比可知,总体上华东模式、欧洲模式、美国模式24 h预报各量级降水风险评分较高。欧洲模式、美国模式暴雨及以上降水风险评分较高,可能得益于空报率和漏报率均较低。华东模式暴雨及以上降水风险评分为最高,除上述原因外,可能还因对暴雨及以上量级降水预报优势明显(王晓峰等,2017),特别是对于对流性暴雨具备较高参考价值(苏翔等,2022)。
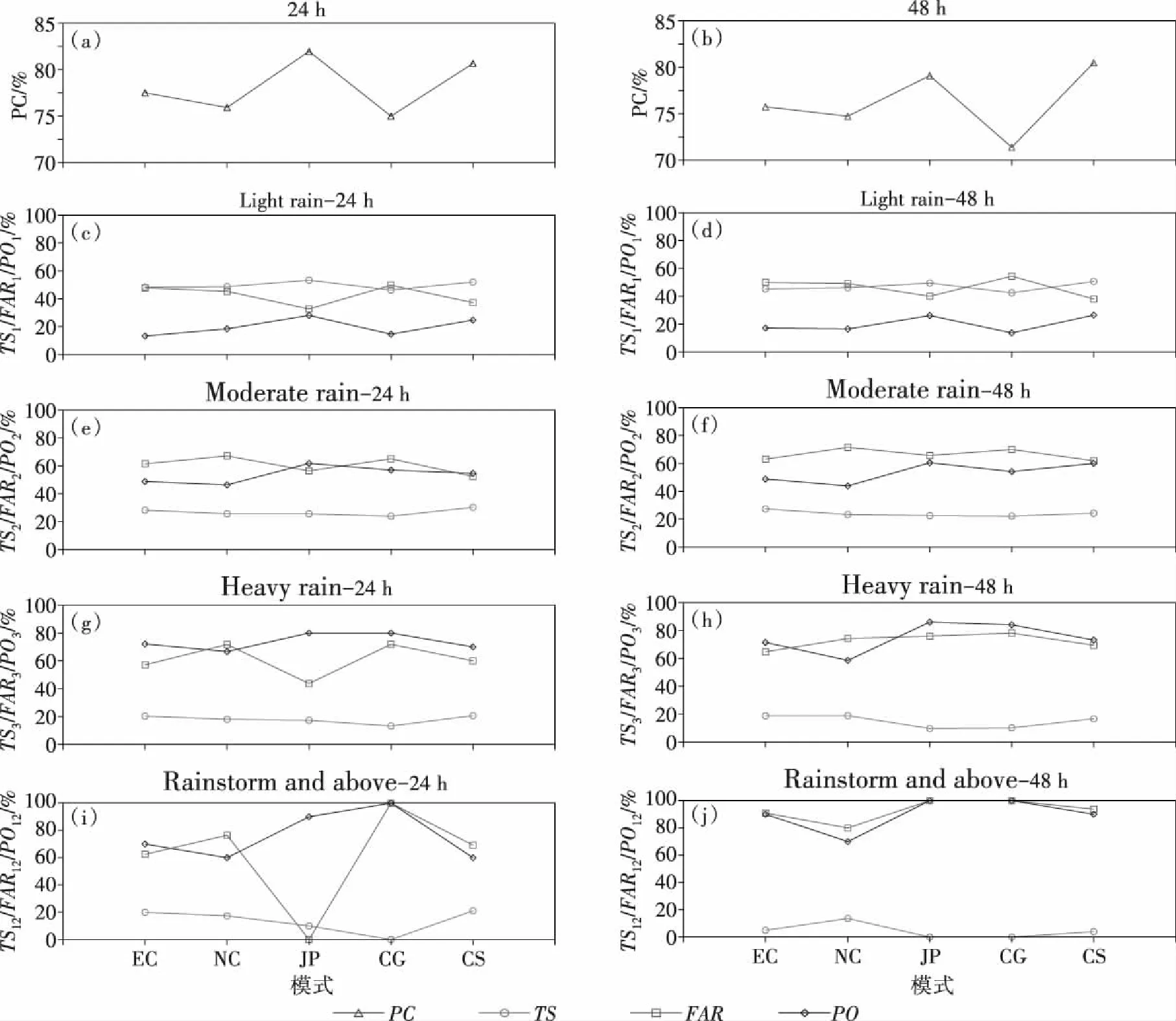
图4 2018—2020年各模式24 h(左)、48 h(右)晴雨准确率(PC)(a、b)以及各量级降水的风险评分(TS)、空报率(FAR)及漏报率(PO)(c—j)
对2018—2020年各模式48 h预报进行分级检验,得到各降水量级风险评分、空报率及漏报率(图4d、4f、4h、4j)。各模式风险评分总体随量级增大而降低,小雨—中雨风险评分大致相当,大雨、暴雨及以上降水风险评分则有较大差异,其中美国模式暴雨及以上降水风险评分较高,其余模式风险评分较低,特别是日本模式、全球模式风险评分为0。各模式空报率总体随量级增大而增大,其中小雨空报率较小,中雨—大雨大致相当,暴雨及以上降水有较大增长,特别是日本模式、全球模式空报率为100%。各模式漏报率总体随量级增大而增大,其中日本模式、全球模式暴雨及以上降水漏报率为100%。进一步对比分析可知,美国模式、欧洲模式、华东模式48 h预报各量级降水风险评分较高,其中美国模式暴雨及以上降水风险评分为最高,可能得益于其空报率及漏报率为各模式最低。
对比24 h及48 h预报分级检验结果可知,总体上各模式24 h和48 h小雨预报风险评分较高,中雨均易空报,大雨均易漏报,暴雨及以上降水均易空报和漏报;总体上各模式24 h预报各量级风险评分高于48 h预报,24 h预报空报率及漏报率低于48 h预报,即总体上各模式24 h预报评分优于48 h预报。
4 订正预报
4.1 设置训练期
根据训练期设置原则,初步设置训练期为1—30 d,计算2018—2020年逐日24 h及48 h降水订正过程中不同训练期内各模式平均权重(图5)。分析可知,24 h降水订正过程中各模式权重分布特征总体与48 h相似,即当训练期较小时,华东模式权重最大,全球模式及日本模式权重相当且较大,欧洲模式及美国模式权重相当且最小;当训练期逐渐增大时,欧洲模式及美国模式权重亦缓慢增大至趋于平缓,全球模式权重则迅速减小,华东模式及日本模式各有增减,但始终均维持较大权重。当训练期增大至约15 d时,各模式权重开始趋于平稳。基于以上分析,为在订正方案中凸显不同模式间权重差异,将训练期修正为1—15 d。

图5 2018—2020年24 h(a)及48 h(b)降水订正过程中不同训练期内各模式平均权重
4.2 订正预报评估检验
基于订正方案,计算2018—2020年逐日24 h及48 h订正预报RF(Revised Forecast)。为验证各季节订正预报效果,使用误差分析及检验方法对整体及分季节订正预报分别进行评估检验。
4.2.1 误差分析
计算24 h、48 h订正预报整体及分季节预报准确率(图6a、6b)、平均绝对误差(图6c、6d)、均方根误差(图6e、6f),并与各模式对比。
对于整体而言,24 h订正预报准确率高于多数模式,24 h平均绝对误差及均方根误差(简称“误差指标”,下同)小于多数模式;48 h订正预报准确率高于多数模式,48 h订正预报误差指标小于所有模式。对比可知,48 h订正预报效果优于24 h。对于各季节而言,冬季24 h订正预报准确率仅高于少数模式,但误差指标小于多数模式;春夏季24 h订正预报准确率高于多数模式,误差指标小于多数模式;秋季24 h订正预报准确率高于所有模式,误差指标小于所有模式;夏季48 h订正预报准确率高于多数模式,平均绝对误差小于多数模式,均方根误差小于所有模式,其余季节48 h订正预报准确率均高于所有模式,误差指标均小于所有模式。
综合以上分析,相对多数模式,无论整体或季节,总体上24 h及48 h订正预报均提高了预报准确率,并减小了误差。可能因订正过程主要参考了总体权重较大的华东模式、日本模式、欧洲模式,而此三种模式无论整体或分季节误差(图略)均较小,多模式集成后能有效减小一部分误差。此外,48 h订正预报效果优于24 h,春秋季24 h、48 h订正预报效果优于冬夏季。
4.2.2 分级检验
图7给出了2018—2020年24 h、48 h订正预报对比各模式晴雨准确率、技巧评分、空报率、漏报率等的差异值。分析可知,24 h及48 h晴雨准确率均高于多数模式。24 h小雨风险评分高于所有模式,空报率、漏报率均低于多数模式;24 h中雨风险评分高于多数模式,空报率低于多数模式,漏报率低于少数模式;24 h大雨风险评分高于多数模式,空报率低于多数模式,漏报率低于少数模式;24 h暴雨及以上降水风险评分高于少数模式,空报率及漏报率均低于少数模式。48 h小雨风险评分高于所有模式,空报率、漏报率均低于多数模式;48 h中雨风险评分高于所有模式,空报率低于所有模式,漏报率低于多数模式;48 h大雨风险评分高于少数模式,空报率低于多数模式,漏报率低于少数模式;48 h暴雨及以上降水风险评分高于多数模式,空报率低于多数模式,漏报率低于少数模式。

表1 2018—2020年24 h、48 h降水订正预报的各模式分季节晴雨准确率(单位:%)
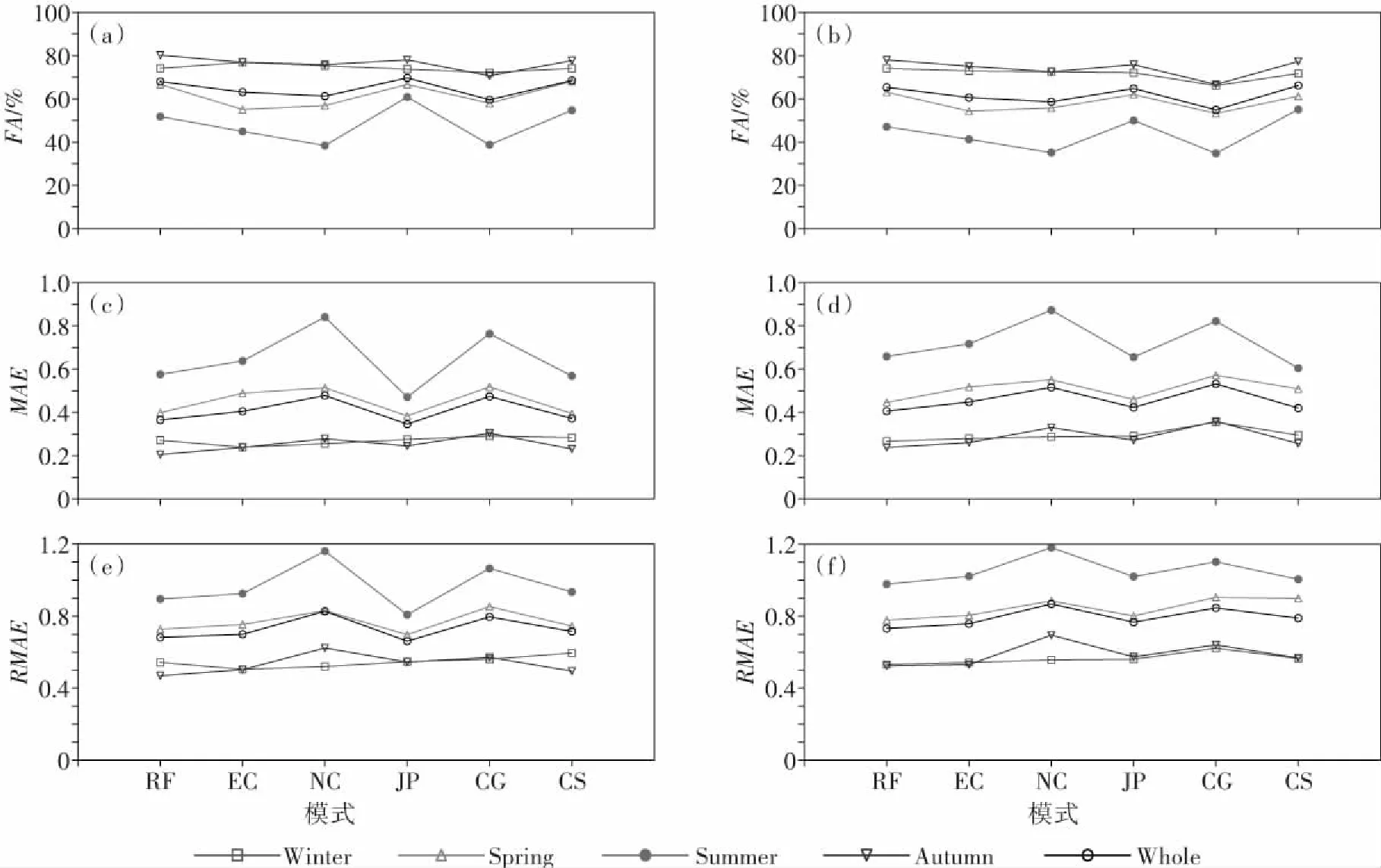
图6 2018—2020年24 h(左)、48 h(右)降水订正预报的各模式整体及分季节预报准确率(a、b)、平均绝对误差(c、d)和均方根误差(e、f)
表1给出了2018—2020年24 h、48 h订正预报对比各模式分季节晴雨准确率。对比可知,24 h与48 h订正效果大体相当;总体上秋季订正效果最优,其次为春夏季,冬季订正效果最差。计算24 h、48 h订正预报各量级降水分季节风险评分、空报率、漏报率并对比各模式,得到订正效果的分布图(图8)。分析可知,除冬季24 h外,各季节24 h、48 h主要提升了小雨—中雨的预报性能,特别是相对所有或多数模式,提高了小雨的风险评分,并降低了小雨—中雨的空报率;对于大雨、暴雨及以上降水改进有限,但仍然提高了夏季48 h暴雨及以上降水的风险评分,并降低了空报率。此外,各季节48 h订正预报效果总体优于24 h;春秋季24 h、48 h订正预报效果总体优于夏冬季。
综合以上分析,相对多数模式,无论整体或分季节,订正预报总体上改进了晴雨准确率,提升了小雨—中雨的预报性能,并提高了夏季48 h暴雨及以上降水的风险评分,同时降低了其空报率。可能的原因如下:1)订正过程主要参考了总体权重较大的华东模式、日本模式、欧洲模式,保证了订正后晴雨准确率总体维持在较大范围;2)订正方程(13)限制了订正预报将以当前最大模式预报值为上限,当预报值较小的模式进入订正流程后,订正预报值将进一步减小,增加了较小量级降水预报准确的可能性;3)由风险评分计算方法(6)知,增加预报准确次数、减小空报或漏报次数均可能提高风险评分。夏季出现暴雨及以上降水次数为全年最多,各模式相应地会增加其预报的次数,当进入订正流程的只有一种模式预报暴雨及以上降水时,订正后预报值将可能减小,能在一定程度上减小暴雨及以上降水空报的次数,进而提高其风险评分。
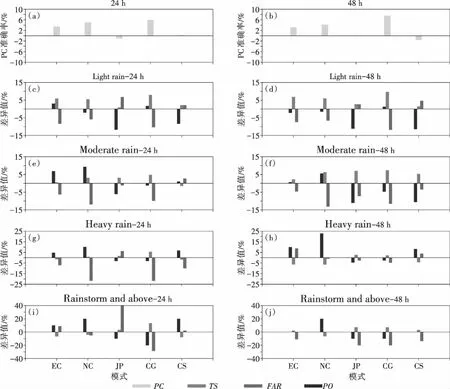
图7 2018—2020年24 h(左)、48 h(右)降水订正预报的各模式晴雨准确率(PC)(a、b)以及技巧评分(TS)、空报率(FAR)、漏报率(PO)的差异值(c—j)
5 结论与讨论
文中对2018—2020年逐日ECWMF、NCEP、JMA、CMA-GFS、CMA-SH9等5种模式24 h和48 h降水预报进行了误差分析及检验,并使用基于平均绝对误差权重的多模式集成订正方案对降水预报作出订正,且对订正结果进行了整体及分季节评估检验,得到如下结论:
1) 总体上各模式24 h、48 h降水量级预报误差均以一个量级的正误差为主,且24 h预报误差小于48 h。华东模式、日本模式24 h、48 h预报误差均较小;总体上各模式24 h预报评分优于48 h;华东模式、日本模式24 h和48 h晴雨准确率均较高;华东模式、欧洲模式、美国模式24 h、48 h预报各量级风险评分均较高;日本模式对24 h暴雨及以上降水可能具有一定的预报指示意义;各模式24 h、48 h风险评分随量级增大而降低,空报率、漏报率随量级增大而增大;各模式24 h、48 h小雨预报性能较优,中雨均易空报,大雨均易漏报,暴雨及以上降水均易空报与漏报。
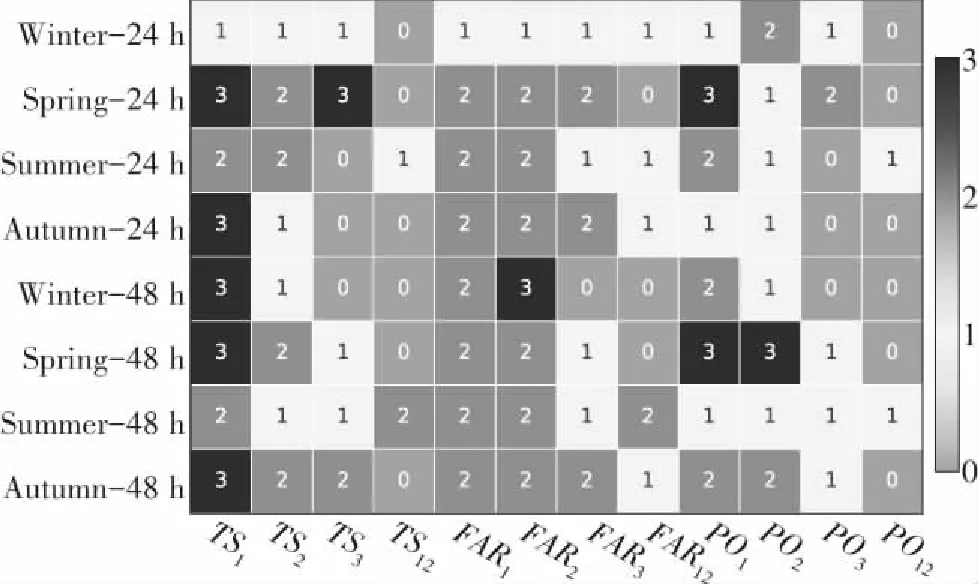
图8 2018—2020年24 h、48 h分季节降水订正预报效果分布(0—3分别表示无改进、较少数有改进、较多数有改进及性能最优)
2) 多数模式经订正后24 h、48 h降水预报性能总体上均有所提升,即提高了预报准确率,减小了预报误差,改进了晴雨准确率,提升了小雨—中雨的预报性能,提高了夏季48 h暴雨及以上降水的风险评分,并降低了其空报率。
3) 48 h降水订正预报效果总体优于24 h,春季及秋季降水订正预报效果总体优于夏季及冬季。
本研究探索了一种站点降水订正方法,但受篇幅所限,未对更多的站点及更长时段进行验证,存在一定的局限性。今后将不断完善订正预报方案,并逐步应用到更多站点,更好地为基层气象台站订正预报提供帮助。

