双超卫星平台柔性线缆构型设计与仿真

李峥，赵艳彬，姚闯，徐毅，谢进进，唐忠兴

双超卫星平台柔性线缆构型设计与仿真

李峥，赵艳彬，姚闯，徐毅，谢进进，唐忠兴

（上海卫星工程研究所，上海 201109）

研究舱间线缆动力学模型及其扰动传递特性，是深入考察连接线缆刚柔耦合效应影响的重要依据。以绝对节点坐标方法（ANCF）三维缩减曲梁单元模型为背景，考虑线缆的大变形特性，构造新的大变形线缆单元弹性力模型。在此基础上，用数值方法对典型约束工况下线缆单元弹性力模型进行计算和分析，获得位移-扰动力线性关系下的两舱振幅范围。此外，结合有限元方法，获得了舱间线缆不同布线构型的等效结构刚度矩阵模型。结果表明：布线过程中合理排列不同材料性能线缆，可有效降低耦合效应的影响，为后续舱间线缆布线规划提供了理论依据。

柔性线缆；大变形；双超卫星平台；动力学建模；仿真分析

0　引言

随着执行高分辨率对地观测、深空探测等任务有效载荷精密程度的提高，对卫星平台提出了超高指向精度、超高稳定度的技术要求［1-2］。对此，上海卫星工程研究所设计了无刚性连接结构的超精超稳双超卫星平台，用于实现载荷模块和卫星平台的动静隔离、主从协同控制［3］。理想双超卫星其载荷模块和服务模块之间完全没有物理连接，但实际中载荷模块与服务模块之间的能量与信息传递需要柔性线缆连接实现，导致了微振动干扰通过连接线缆向载荷舱的传播。因此准确分析舱间线缆在工作状态下的动力学行为，降低线缆耦合效应对双超卫星平台性能的影响有重要的工程意义。

PEDREIRO等［4］首先将非接触平台的连接线缆和非接触式作动器反电动势作为两舱耦合源，通过实验的方法分析了耦合效应对载荷模块的性能影响。刘磊等［5］和ZHOU等［6］基于拉格朗日法建立柔性线缆连接的非接触平台刚柔耦合动力学模型，通过仿真研究柔性线缆对非接触平台隔振性能和指向性能的影响，结果表明载荷模块与服务模块之间存在柔性线缆耦合时，其低频段隔振性能较完全非接触情况下降90%以下，这说明柔性线缆对双超卫星平台的低频段隔振性能造成了较大的影响。LIU等［7］针对非接触式作动器反电动势等耦合特性提出了一种基于模型预测控制的两舱避碰控制策略。WU等［8-9］基于弹性细杆的力学模型，建立了柔性线缆的多自由度非线性力学模型，研究了磁悬浮隔振系统柔性线缆的传递特性。YANG等［10］基于此项研究提出了基于该模型的扰动前馈补偿控制策略。LIAO等［11-12］为避免非接触界面耦合效应的影响，提出了一种基于无线构型的事件触发姿态跟踪控制策略。此外，ARDELEAN等［13］通过实验方法对电缆的精密结构动力学建模方法进行了研究。以上研究都是基于柔性线缆耦合效应分析非接触平台的性能变化现象，没有针对舱间线缆动力学特性提出具体的优化策略。

为降低柔性线缆耦合现象对双超卫星平台隔振性能以及指向性能的影响，本文针对线缆的柔性和大变形特性［14-15］，基于绝对节点坐标方法（Absolute Nodal Coordinate Formulation，ANCF）单元力学模型［16］，建立柔性线缆的多自由度非线性动力学模型，并提出柔性线缆扰动力的线性假设。基于此假设，通过有限元仿真的方法研究线性运动范围内不同布线方式对载荷模块的性能影响，得到最优线缆布线构型，为降低耦合效应影响提出布线方案。

1　ANCF线缆单元变形描述

现有研究成果显示，线缆剪切和扭转效应对两舱平台的影响较小［17-18］，本章在仅考虑线缆的拉伸和弯曲变形前提下，采用ANCF三维缩减曲梁单元对初始构型为半圆形的线缆进行研究，如图1所示，分别在有无重力作用下研究线缆两端对载荷平台产生的约束反力和反力矩。

图1　线缆初始构型

基于Euler-Bernoulli梁假设的ANCF缩减三维曲梁单元如图2所示。该梁单元初始长度为l，具有2个节点，每个节点有6个绝对坐标，从而有如下12个绝对节点坐标组成的列向量：

由Euler-Bernoulli梁假设可知，梁单元变形过程中截面形状保持不变，并且其法线方向与中线方向一致。因此，初始构型中梁单元上任一点的位置矢量可表示为

考虑舱间连接线缆大应变的运动特性，研究过程中需要考虑线缆单元的拉伸变形与弯曲变形的耦合效应、应变-位移与应力-应变的双重耦合非线性关系。因此采用Green-Lagrange应变对线缆单元变形进行描述。

根据Green-Lagrange应变张量的定义，在点的Green-Lagrange应变张量可表示为

2　单根线缆约束力（矩）求解

在得到梁单元上任一点的应变张量后，通过对该单元初始构形的体积分，单元应变能可表示为

单元的弹性力可通过应变能对广义坐标求一次偏导数得

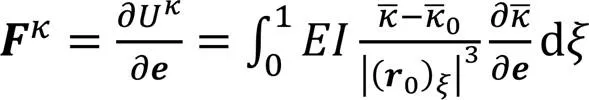
基于以上模型，采用Newton-Raphson迭代进行准静态求解其最终状态时对平台的约束反力（矩）。约束反力和力矩随平台端矩的变化规律如图3所示。

图3　约束反力和力矩随平台端矩的变化规律

仿真结果表明：对于初始构型为半圆形的线缆，当两舱平台的振动幅值较小时（线缆跨度的10%），线缆对两舱平台的约束反力及反力矩均与平台的位移近似成正比。

考虑实际情况［19-20］，双超卫星平台振动量级在此范围内，因此后续仿真工作中可以假设线缆对平台的约束反力（矩）与平台的位移成正比。

3　柔性线缆布线构型仿真分析

基于以下线性假设：当两舱平台的振幅在一定范围时（线缆跨度的10%），线缆对两舱平台的约束反力（矩）均近似为平台位移的线性函数。舱间线缆扰动力（矩）可表示为双超卫星平台两舱位移的线性函数，求得线缆的等效结构刚度矩阵即可建立柔性线缆的等效动力学模型。

采用有限元方法仿真求解舱间线缆的结构刚度矩阵，研究线性运动范围内不同布线方式线缆对载荷模块性能的影响。先仿真得到单根线缆的固有模态，再具体分析多线缆布线构型方案。有限元仿真得到线性运动范围内的结构柔度矩阵，通过求逆变换得到结构刚度矩阵。线缆基本仿真参数见表1。

表1　线缆基本仿真参数

3.1　单根线缆模态

仿真得到2种线缆前8阶固有频率见表2，前4阶固有振型如图4所示，线缆布线模型如图5所示。

表2　单根线缆固有频率仿真结果

图4　线缆前4阶模态振型图

图5　线缆布线模型示意图

3.2　多线缆布线构型仿真分析

为了比较4种不同的布线方式对载荷模块的影响程度，在线缆端部的6个自由度上施加位移激励，通过线缆末端的响应，分析不同布线方式的耦合特性。线缆的等效动力学模型可以表示为

在线缆首端6个自由度施加正弦位移激励：

端部施加位移激励时线缆末端的扰动力（矩）响应曲线如图6所示。

图6　线缆末端扰动力（矩）响应曲线

布线方法1～方法3均使线缆扰动力（矩）产生不同程度的减小，其中方法1相较于方法4，平移自由度端部扰动力降低25.1%，转动自由度端部扰动力矩降低67.0%；且方法1和方法2在激励幅值增加的情况下产生的末端力矩响应性能更优秀。因此方法1对降低线缆耦合效应影响的效果最优。

4　结束语

1）基于ANCF缩减曲梁单元提出了适用于大变形线缆单元弹性力模型的构造方法，建立线缆单元弹性力模型并求得数值解，提出线缆对非接触平台约束反力的线性假设。

2）在线性假设运动基础上，利用有限元仿真得到线缆不同布线方式的等效动力学模型，通过线缆末端扰动力（矩）响应研究不同布线方法对双超卫星平台性能影响，从而提出了多线缆的最佳布线构型。

3）本文的研究着重考虑了线性假设内的线缆约束反力（矩）规律，若要进一步深入研究柔性线缆对两舱性能影响，还需要针对不同初始构型、不同振动幅值的工作状态以及复杂工况下扰动的定量表述方式进行更为充分的研究。在此基础上开展的线缆动力学建模、定量分析将会成为后续工作的主要内容。

［1］ 吴季，孙丽琳，尤亮，等.2016—2030年中国空间科学发展规划建议［J］.中国科学院院刊，2015，30（6）：707-720.

［2］ PEDREIRO N. Next generation space telescope pointing stability［C］// AIAA Guidance， Navigation， and Control Conference and Exhibit. Denver， CO：American Institute of Aeronautics and Astronautics， 2000： 4543.

［3］ 张伟，赵艳彬，廖鹤，等.动静隔离、主从协同控制双超卫星平台设计［J］.上海航天，2014，31（5）：7-11，30.

［4］ PEDREIRO N， GONZALES M， FOSTER B， et al. Agile disturbance free payload［C］// AIAA Guidance， Navigation， and Control Conference and Exhibit. San Francisco， California：American Institute of Aeronautics and Astronautics， 2005： 5876.

［5］ 庞岩，李静，刘磊.柔性线缆连接的分离式卫星动力学建模［J］.宇航学报，2017，38（1）：1-9.

［6］ ZHOU J， WANG Z， LI W， et al. Modeling and pointing performance analysis of disturbance-free-payload system with flexible umbilical connection［J］. IEEE Access， 2019， 7： 109585-109596.

［7］ YANG H， LIU L， YUN H， et al. Modeling and collision avoidance control for the disturbance-free payload spacecraft［J］. Acta Astronautica， 2019， 164： 415-424.

［8］ WU Q， LIU B， CUI N， et al. Dynamic analysis of umbilical cables for maglev vibration isolation systems［J］. AIAA Journal， 2019， 57（4）： 1752-1762.

［9］ 武倩倩.六自由度磁悬浮隔振系统及其力学特性研究［D］.哈尔滨：哈尔滨工业大学，2016.

［10］ YANG H， LIU L， LIU Y， et al. Modeling and micro-vibration control of flexible cable for disturbance-free payload spacecraft［J］. Microgravity Science and Technology， 2021， 33（4）： 1-16.

［11］ LIAO H， XU Y， ZHU Z， et al. A new design of drag-free and attitude control based on non-contact satellite［J］. ISA Transactions， 2019， 88： 62-72.

［12］ QI J， LIAO H， XU Y， et al. Event-triggered attitude-tracking control for a cableless non-contact close-proximity formation satellite［J］. Aerospace， 2022， 9（3）： 138.

［13］ ARDELEAN E V， BABUŠKA V， GOODDING J C， et al. Cable effects study： tangents， rabbit holes， dead ends， and valuable results［J］. Journal of Spacecraft and Rockets， 2015， 52（2）： 569-583.

［14］ 游斌弟，郑天骄，陈军，等.含空间约束航天器线缆力学建模方法［J］.振动与冲击，2015，34（16）：8-13.

［15］ 游斌弟，郑天骄，陈军，等.拖拽下大变形柔性线缆力学特性分析与测试［J］.机械工程学报，2015，51（23）：36-45.

［16］ 於祖庆，兰朋，李昆昆，等.基于分段连续ANCF缆索单元的输电线缆动力学建模与仿真［J］.机械工程学报，2018，54（19）：70-77.

［17］ DEWELL L， PEDREIRO N， BLAUROCK C， et al. Precision telescope pointing and spacecraft vibration isolation for the terrestrial planet finder coronagraph［C］// UV/Optical/IR Space Telescopes： Innovative Technologies and Concepts Ⅱ. International Society for Optics and Photonics， 2005： 589902.

［18］ REGEHR M. Analysis of a near-free-floating vibration isolation platform［R］. Interplanetary Network Progress Report， 2015： 42-200.

［19］ 杨鸿杰，刘磊，李新国.超静空间科学卫星分离式主动隔振技术［J］.中国空间科学技术，2021，41（4）：102-110.

［20］ KONG Y， HUANG H. Performance enhancement of disturbance-free payload with a novel design of architecture and control［J］. Acta Astronautica， 2019， 159： 238-249.

Configuration Design and Simulation of Flexible Cables for Dual-super Satellite Platform

LIZheng， ZHAOYanbin， YAOChuang， XUYi， XIEJinjin， TANGZhongxing

（Shanghai Institute of Satellite Engineering， Shanghai 201109， China）

The dynamics model and disturbance transfer characteristics of cabin cables are always an important basis for the research on the rigid-flexible coupling effect of the connecting cables. In view of this， a new elastic force model for large deformation cable elements is built based on the three-dimensional （3D） reduced curved beam element model of absolute nodal coordinate formulation （ANCF）. Then， the elastic force model under typical constraint conditions is calculated and analyzed numerically， and an amplitude range under the linear relationship of the displacement and the disturbance force is obtained. Furthermore， the equivalent structural stiffness matrix of different arrangements of cables is obtained with the finite element method. The results show that the effect of coupling induction can be reduced effectively by the reasonably arrangement of different cables. The conclusions are of important engineering significance for the mechanics modeling of flexible cables and the routing processes.

flexible cable； large deformation； dual-super satellite platform； dynamics modeling； simulation analysis

2022‑01‑27；

2022‑08‑01

上海市“科技创新行动计划”启明星项目（21QA1408500）；国家自然科学基金（41971412，42171341，12172168）

李峥（1998—），男，硕士研究生，主要研究方向为动力学与控制。

赵艳彬（1975—），男，博士，研究员，主要研究方向为飞行器总体设计、动力学与控制等。

V 412.4

A

10.19328/j.cnki.2096⁃8655.2022.04.017