一类半线性退化Schrödinger方程解的存在性
冉 玲,陈尚杰,李 麟
(重庆工商大学 数学与统计学院,重庆 400067)
1 关于半线性退化Schrödinger方程的介绍和主要结论
本文主要研究如下半线性退化Schrödinger方程
(1)
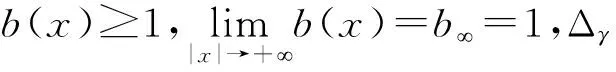
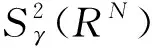
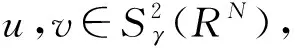
其中∇γ=(γ1∂x1u,…,γN∂xNu)。
退化算子Δγ中的函数γj:RN→R是连续的,是RNΠ上不等于零的C1函数,其中:
而且,函数γj满足如下条件[1]:
1)存在一个扩张{δt}t>0的半群使得δt:RN→R,δt(x1,…,xN)=(tε1x1,…,tεNxN),其中1=ε1≤ε2≤…≤εN,使函数γj关于δt是εj-1阶齐次的,即:
γj(δt(x))=tεj-1γj(x),∀x∈RN,∀t>0,j=1,…,N,
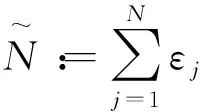
2)γ1=1,γj(x)=γj(x1,x2,…,xj-1),j=2,…,N;
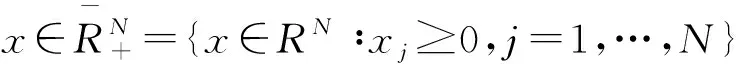
4)等式γj(x)=γj(x*)(j=1,…,N)对任意x∈RN成立,这里x*=(|x1|,|x2|,…,|xN|);
5)等式γj(x+z)=γj(x)(j=1,…,N)对任意x∈RN和z∈ZN成立。
退化算子Δγ包含了如下的Grušin型算子:
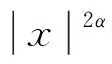
其中(x,y)表示RN1×RN2中的点。GRUIN[2]研究了α是整数的情况,Franchi和Lanconelli[3-4]研究了α不是整数的情况。Δγ算子还包含如下强退化算子:
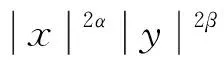
其中α,β是非负常数,Anh[5]研究了这个算子Pα,β。在文献[1]中有关于Δγ算子的更多信息介绍。
目前,Anh和My[6],Luyen等[7]及Chen等[8]在RN的有界域Ω中研究了半线性退化Schrödinger方程解的存在性及多解的存在性问题,在有界区域中对于方程所对应的能量泛函所在的空间嵌入到Lq(Ω)中的紧性是很容易得到的,但是本研究的方程是在RN上进行的,加大了研究的难度。在RN上的带Δγ算子的半线性椭圆型偏微分方程解的存在性的研究结果还相当稀少,仅Luyen和Tri[9]运用对称山路定理得到了如下的带Δγ算子的半线性椭圆型偏微分方程
(2)
无穷多解的存在性,其函数空间是:
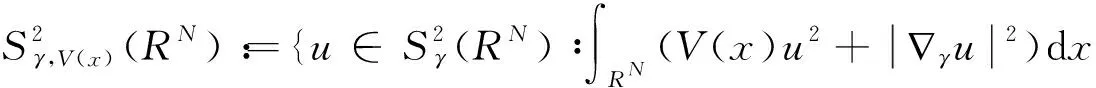
其中位势函数V(x)满足:对任何实数C>0集合{x∈RN∶V(x) 本文考察带有常数位势函数的带Δγ算子的椭圆型偏微分方程(1)解的存在性,结果如下: 1)b∈L∞(RN)且b(x)≥1,∀x∈RN; 则方程(1)至少有一个非平凡解。 为了完成定理的证明,需要如下的临界点定理[10]: 定理2(山路定理)假设H是Banach空间,J∈C1(H,R)满足J(0)=0,存在正常数α和ρ使得 1)当‖u‖H=ρ时,J(u)≥α; 2)存在v∈H使得‖v‖H>ρ且J(v)<0; 如果J满足(PS)c条件,则c是J的临界值,这里 首先考虑极限情形,即方程(1)中的b(x)=b∞=1时非平凡解的存在性,也就是考虑方程 (3) (4) (5) (6) 证明取{un}⊂B是Sp+1的极小化序列,即当n→∞时有|un|p+1=1,‖un‖2→Sp+1。根据文献[10]中的引理2.1得 其中B(y,1)表示以y为圆心1为半径的球。由此可知存在序列{yn}⊂RN使得 (7) 令vn(x)=un(x+zn),通过平移不变性得 |vn|p+1=1,‖vn‖2→Sp+1, (8) (9) 根据文献[11]的Brézis-Lieb引理:如果hj∈Lq(RN),q∈(1,∞)是有界的并且几乎处处在RN中有hj(x)→h(x),则 (10) 从而易得 (11) 由Sobolev不等式和(11)式可得 函数t在(-ε,ε)上是可导的,其导函数如下: 由上可得 (12) 即 (13) (14) (15) 1)当‖u‖=ρ时,Jb(u)≥α; 证明根据Jb(u)的定义显然有Jb(0)=0。 1) 从(6)式可得 因此,存在实数M>0,当t>M时,有v=te0满足‖v‖>ρ以及Jb(v)<0。 引理4 假设函数b(x)满足定理1中条件1),2)成立,则泛函Jb(u)满足(PS)cb条件,这里 Jb(un)→cb,J′b(un)→0。 (16) 显然当n充分大时, (17) (18) 根据(18)式以及(un-u1,u1)=o(1),显然 =Jb(un-u1)+Jb(u1)+o(1)。 结合(16)式以及(17)式,推出 Jb(un-u1)≤cb+o(1)。 (19) 通过相似的方法,有 因为〈J′b(u1),u1〉=0并且当n→∞时,〈J′b(un),un〉=0,可得存在β≥0满足 (20) 由定理1中条件2可推出对任何ε>0,当n,R充分大时有 从而由(20)式可知 (21) 结论与前面c∞>cb矛盾。因此β=0,则‖un-u1‖2=0,泛函Jb(u)满足(PS)cb条件。 本文主要对带有Δγ算子的Schrödinger方程进行了研究,利用山路定理以及变分法找到带有Δγ算子的Schrödinger方程非平凡解的存在性,所研究的方程中b(x)是渐进常数的,如果将b(x)换成渐进线性的,是否同样可以得到带有Δγ算子的Schrödinger方程非平凡解的存在性呢?这将是未来研究工作之一。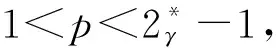
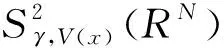
2 变分结构和定理证明
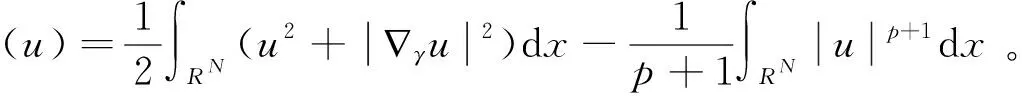
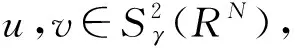
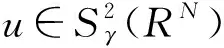
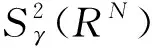
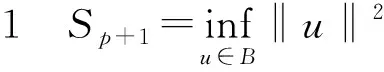
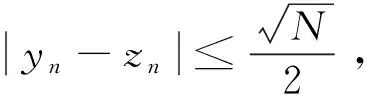
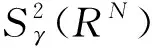
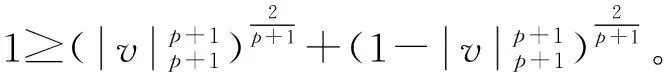
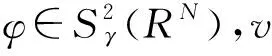
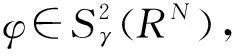
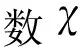
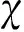
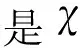
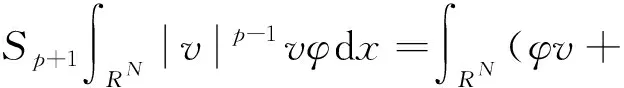
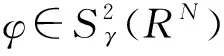
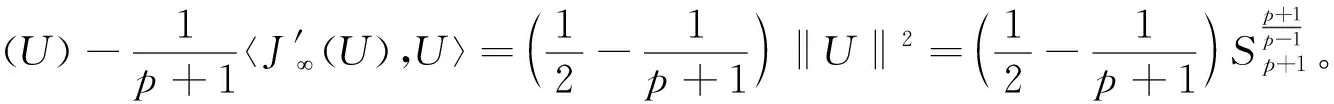
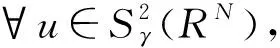
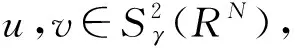
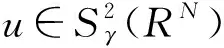
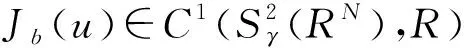
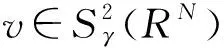
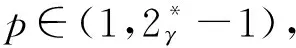
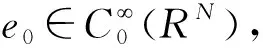
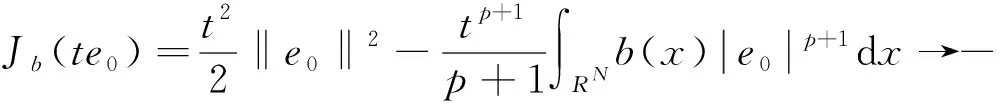
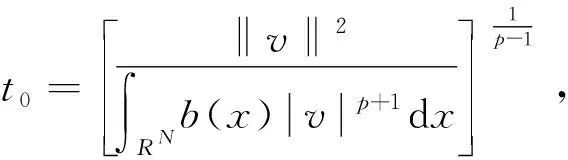
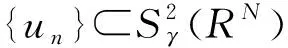
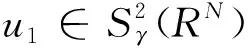
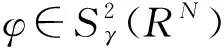
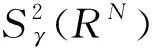
3 结 语

