价格机制与空间失衡:空间经济学的发展、应用与挑战*
莫家伟,范剑勇
一、引言
经济的空间分布不平衡是当今世界经济的显著特征之一(Krugman,1991;陆铭等,2011)。在中国,这种空间不平衡显得尤为明显。2021年,北上广深四个城市以0.6%的土地,聚集了全国5.9%的人口,产出了全国12.4%的国内生产总值①土地指行政区划面积,人口指常住人口,国内生产总值系当年名义价格。数据来源是国家统计局和CEIC数据库。。对于中国这样的领土广阔、人口基数庞大的国家,应该追求怎样的空间经济分布,从而在“双循环”新发展格局下更好地实现国民福利最大化?回答这一基本问题往往涉及空间经济学的空间均衡理论。
空间均衡(Spatial Equilibrium)在本文系指居民和企业不存在空间上的迁移动机,即居民在不同地方的效用相等以及企业在不同地方的利润相等。相对应地,空间失衡(Spatial Disequilibrium)系指部分或所有居民和企业存在迁移动机,即不同地方的人口和企业数量不存在稳定状态,个别区域可能形成空间“黑洞”情况。需要说明的是,空间均衡不等于人口的平衡分布,也不与空间集聚对立。空间均衡的核心是人口空间分布的稳定性。
本文尝试回答的问题是,理论上在什么条件下存在空间均衡?如果现实不满足空间均衡存在的条件,那么会产生两个难题。第一,研究者无法分析和判断城市人口变动的方向,更遑论分析最优城市人口规模和空间经济分布。第二,价格机制在空间维度失灵。土地价格,尤其是房价,是空间上阻碍人口和企业进入的核心市场力量(以下称为市场离散力或离心力)①相对应地,市场集聚力是空间上吸引人口和企业进入的市场力量。空间集聚力或离散力包括市场力量和政府政策提供的力量。。假如不存在空间均衡,则不存在均衡的城市人口,那么房价也将始终处于非稳定状态,并由此可能产生经济和金融风险。
Starret(1978)较早提出了关于价格机制的“空间不可能定理”,证明在空间同质、完全竞争和交通成本不为零的条件下,不存在一组市场价格使得劳动者和企业的迁移动机为零②空间同质系指居民和企业对不同地方的偏好无差异,这里可以理解为不同地方的自然和人文社会环境等均一致。。Proost&Thisse(2019)进一步指出,“空间不可能定理”的根源在于价格系统无法同时完成两个任务:在支撑区域间的商品和要素贸易的同时阻止居民和企业迁移。近半个世纪以来,空间均衡理论的发展主要引入空间异质性或(和)不完全竞争,以应对空间不可能定理的理论挑战。同时,为了对现实空间数据提供更好的解释力,空间均衡理论引入复杂交通网络和异质性企业和消费者。
然而,本文通过回顾空间经济理论的最新发展指出,不管是引入空间异质性的经典空间均衡模型,抑或是引入垄断竞争的新经济地理模型,还是同时引入两者的量化空间均衡模型,都无法保证价格机制能够同时实现市场和空间的双重均衡。本文进一步以量化区域模型为例,通过比较完全竞争和垄断竞争下模型均衡解的存在性和唯一性的参数条件,发现两种的参数条件恰好相反。由于垄断竞争假设比完全竞争假设多一层以本地市场效应为核心的市场集聚力,其参数条件要求增强空间离散力,导致参数条件与完全竞争假设相反。本文指出,实现市场和空间的双重均衡的条件总体要求市场的多种集聚力和离散力保持相对平衡,即市场集聚力既不能过大,也不能过小,否则不存在空间均衡。这是本文与Proost&Thisse(2019)和刘修岩等(2021)的综述在侧重点上的核心区别。
基于对空间经济理论发展的讨论,本文认为,在空间失衡的情况下,引入政府空间政策调整空间集聚力或离散力是对市场价格机制的必要补充,是维持空间集聚力与离散力相对平衡的重要方式,可以更好地实现空间均衡和经济稳定。本文关于政府空间政策的论述是初步探讨,作抛砖引玉之用,希望能引起研究者对西方经济理论的空间适用性的更多思考,特别是对于中国这样的大国,可能需要适用于基本国情的理论分析。
本文的结构安排如下:第二节围绕空间不可能定理的条件对空间均衡理论的最新发展和潜在挑战进行回顾与分析;第三节以量化区域模型为例,比较不同市场结构假设下模型解的存在性和唯一性的参数条件的区别;最后一节是总结。
二、空间经济理论的发展与应用
理论上是否存在经济活动的最优空间分布?对于中国这样的大国经济,未来空间管理的方向是什么?这一节将围绕这些问题,对空间经济理论的发展、应用和面临的挑战进行梳理。我们根据空间质性和市场竞争结构两个维度,将空间经济理论划分为四个类别(见表1)。空间质性包括空间同质性和空间异质性,前者假设消费者和生产者对不同空间位置的偏好无差异,后者假设空间存在异质性,可能影响消费者的效用或(和)生产者的生产技术。市场竞争结构包括完全竞争和不完全竞争,前者假设消费者和生产者都是价格的接受者,后者假设厂商存在一定程度的市场垄断力量。我们首先对四类代表性理论分别进行梳理,然后回顾空间经济理论的应用。

表1 空间经济理论的类型
(一)空间不可能定理
现有的空间经济学相关教材较少将“空间不可能定理”放在核心的位置。本文认为,空间不可能定理是空间经济学的基准性理论,是后续空间经济理论发展和拓展绕不开的问题和面临挑战的根本来源。
什么是空间不可能定理?其核心回答的问题是,完全竞争下的一般均衡模型是否能解释商品在空间上的分配。一部分著名学者如帕累托(Pareto)、瓦尔拉斯(Walras)和希克斯(Hicks)等认为答案是肯定的,只要把商品的地址看作是商品的一个特征,对商品进行适当的分类和排序,就可以把空间问题转化为一般的商品问题(Arrow&Debreu,1954)。另一部分学者如卡尔多(Kaldor,1935)和伊萨德(Isard,1949)等则认为答案是否定的,问题并没有那么简单,特别是需要考虑资本和劳动力的迁移动机和空间均衡。他们指出,核心问题是存在正的交通成本(Fujita,2010)。随着时间的推移,研究者们逐渐意识到空间分配问题不存在完全竞争下的一般均衡。
为什么交通成本的存在会导致空间分配不存在竞争均衡?Starret(1978)通过计算劳动者和企业的迁移动机,证明当空间是同质且存在正的交通成本时,劳动者和企业加总的净迁移动机永远为正,且该动机大小不可忽略,与加总的交通成本成正比,即交通成本越大,双方越有动机迁移到消费需求地或者企业工作地。原因在于,跨区域贸易的发生代表对方愿意支付包含交通成本的商品或者服务。既然对方的支付意愿足够高,那么企业就有动机迁移到商品购买方的所在地,将节省的交通成本转化为利润,同时劳动者也有动机迁移到企业所在地节省通勤成本。①这里假设企业和个人可以自由选择区位,不存在迁移成本。因此,不存在一套商品价格和工资机制,既能支撑跨区域贸易,又使得劳动者和企业稳定在某种空间分配中。需要注意的是,这里假设大家都是价格的接受者,迁移不会影响价格系统。
基于Starret(1978)的讨论,空间不可能定理可以概括为,当消费者偏好和企业生产技术均与所在区位(location)无关(即空间同质),且区位间的商品交易存在正的交通成本时,不存在涉及跨区位商品交易的竞争均衡(competitive equilibrium)。
Proost&Thisse(2019)通过反证法对空间不可能定理给出更简单的证明。首先,根据福利经济学第一定理,如果存在竞争性均衡,那么均衡肯定是帕累托最优。因此,在给定的最优市场价格下,经济体的总生产成本加上总交通成本一定是最小的,即有以下等式的成立:

其中,n是商品种类,qi是第i个商品的最优产量。生产第i个产品的边际成本(Cqi)加上其边际交通成本(Tqi)之和一定等于零。注意这里都是最优价格下的均衡产量。我们知道交通的边际成本永远大于零,即Tqi>0。因此,必然有Cqi<0。但是竞争均衡中的厂商利润最大化不可能存在边际成本为负的情况。反过来,如果边际生产成本为非负,必然要求交通的边际成本为零,那就只可能存在自给自足的情况,所有经济活动在空间上无限分割,没有跨区位贸易。显然,这在现实中是不可能的,由此得证不存在竞争均衡。
空间不可能定理指出,关于企业和劳动力的空间分配问题不能在竞争性一般均衡的框架下分析相关的效率和福利问题。由此带来的问题是,我们难以定义什么是空间最优∕最有效率的分配。要同时实现市场和空间的双重均衡,我们必须引入一个或多个核心假设:
(a)空间异质性
(b)不完全竞争
(c)外部性
在空间上引入(a)条件,假设空间异质性的代表性理论是国际贸易领域的李嘉图比较优势理论和H-O理论,以及城市经济学领域经典的Rosen-Roback模型。不同地区假设生产率或者要素禀赋存在差异,因而存在最优的生产分配使得总消费最大。这类模型的问题是,我们外生地引入空间异质性,无法知道为什么不同地方会存在生产率或者禀赋差异,也无法知道为什么某些地方成为了空间的经济中心。此外,国际贸易理论基本不讨论人的跨国迁移的问题。
引入(b)条件,假设不完全竞争的代表性理论是克鲁格曼的新经济地理模型,即“中心—外围”模型。这类模型在假设地区同质的同时引入垄断竞争和规模报酬递增,能够解释在交通成本足够小但不为零的情况下,企业和工人为了节省交通成本和获取规模报酬递增收益而集聚到某个地区形成中心。该模型将经济地理带入了一般均衡分析框架,但无法判断哪个地区会成为中心,需要结合现实的初始条件差异进行判断。最后,对于(c)条件,假设的外部性,可以理解为(a)条件下的某种空间异质性或者内嵌于(b)条件下的某种空间集聚力。
(二)空间异质、完全竞争下的经典空间均衡模型
在国际贸易领域,李嘉图模型假设不同国家生产不同产品的生产率存在差异,证明每个国家出口自己具有比较优势的产品和进口缺乏比较优势的产品能够实现社会福利最大化。H-O模型假设不同国家的资本和劳动力禀赋结构存在差异,指出各个国家将出口使用自己相对密集禀赋的产品,进口使用相对稀缺禀赋的产品。这两个经典空间模型不涉及空间均衡问题,因为假设资本和劳动力都不存在跨国流动。当考虑资本跨国流动时,例如FDI和OFDI,则需要加入资本在空间上实现利润均等的条件实现资本的空间均衡。
在城市经济学领域,通常假设不同城市的便利环境(amenity)存在差异。便利环境含义很广泛,包括自然气候条件、社会人文环境和公共服务设施等。假设资本和劳动力可以自由进入和退出城市分别实现利润和效用最大化。资本和劳动力实现空间均衡的条件分别是资本利润的空间均等化和劳动力效用的空间均等化(Roback,1982)。由此得到均衡的要素价格是城市便利环境的函数。
劳动力的空间均衡条件一般可以表示为:
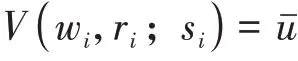
其中,V是间接效用函数,wi,ri和si分别是城市i的工资、土地租金和城市便利环境,uˉ是各个城市均等的效用水平。当劳动者在城市i的效用高于uˉ时,其他劳动者会进入该城市,提高土地价格或降低工资水平,从而降低该城市效用水平;当低于uˉ时,该劳动者会离开该城市选择其他城市,土地价格下降或工资上升,从而提高该城市效用水平。最终的均衡状态是选择任意城市的效用均一致。假如使用Cobb-Douglas效用函数,一般我们会得到:名义工资-租金+舒适环境=外部效用(范剑勇等,2015)。劳动力的空间均衡的本质是劳动力在各个区位的真实工资达到一致,从而使得劳动力没有迁移动机。
资本(或企业)的空间均衡条件一般表示为:

其中,C是单位产品的生产成本,wi,ri和si分别是城市i的工资、土地租金和城市便利环境,pˉ是完全竞争下均等的产品价格水平,与城市i无关。这里假设生产函数是规模报酬不变。当单位成本高于价格时,企业选择退出该城市,工资下降或者租金下降,从而单位成本下降;当单位成本低于价格时,更多企业选择进入该城市,工资上升或租金上升,从而单位成本上升。企业的空间均衡的本质是企业在各个区位的经济利润达到一致,从而使得企业没有迁移动机。
结合劳动力和资本的空间均衡条件,可以求出均衡状态下的工资和租金,同时分析城市便利环境的变化如何影响均衡工资和租金。
空间异质性除了城市的便利环境,城市的土地或房屋供给情况也存在差异。土地供给限制既包括自然地理状况,也包含政府的城市规划和土地利用限制等。Glaeser et al.(2006)构建包含房屋供给弹性的劳动力空间均衡模型,分析房屋供给弹性的异质性如何影响生产率冲击对城市扩张的作用。
上述包含空间异质性的空间均衡分析框架并没有直接讨论交通运输成本对商品和劳动力市场的影响。我们可以将该城市内部的平均交通通达度理解为城市的一种便利条件(si),从而分析城市交通对均衡工资和租金的影响,例如Harari(2020)将城市形状理解为市内平均交通通达度的程度,作为城市的一种便利条件。然而这种方法不能准确地刻画复杂交通网络对于不同目的地运输成本的影响和交通网络的一般均衡效应。
此外,上述分析框架仍未解决“空间不可能定理”指出的“一石不能打二鸟”的问题。上述框架中的要素价格完全由空间迁移动机,即(si)决定,而非由各个区位的要素市场的供需决定。因此,该框架无法保证要素市场出清下的要素价格等于空间均衡下的要素价格。
(三)空间同质、不完全竞争下的新经济地理模型
在空间同质的情况下解释市场自发形成空间的经济中心的机制是有困难的。Krugman(1991)通过放松完全竞争市场的假设,引入垄断竞争,一定程度上避免“空间不可能定理”的双重均衡挑战,并揭示了制造业自发集聚到某个地区的机制。具体而言,Krugman(1991)引入了产品多样性偏好和垄断竞争假设。产品多样性偏好最早可追溯至Armington(1969)关于同类产品差异化的一般理论。垄断竞争的分析框架最早由Chamberlin(1933)等建立,Dixit&Stiglitz(1977)通过结合产品多样性偏好进一步拓展垄断竞争模型。垄断竞争假设在分析上的精妙之处在于,两个地区的产品种类或者厂商数目之比等于两个地区的劳动力规模之比。当一个地区劳动力规模增大,其能享受到的产品种类将增加,从而提高该地区的效用水平并反过来吸引更多的人口,形成一种正向的反馈机制。
以Krugman(1991)为代表的新经济地理模型的贡献在于,即使在空间同质的前提下,其仍能解释什么情况下市场会自发形成制造业中心,什么情况下制造业会分散在不同地方。当工业品消费份额比较小的时候,或者规模经济比较弱且交通成本比较高的时候,制造业会分散分布,因为集聚收益并不大。当工业品消费份额比较大,或者规模经济较强且交通成本较小时,制造业会集中在其中某个地区。
不完全竞争下的空间均衡的核心取舍是,一方面集聚本身创造需求,集聚可以获得规模报酬递增和更高的收益,这是主要的市场集聚力;另一方面,集聚本身加剧市场竞争,特别是对固定需求的农民的竞争或者对稀缺土地区位的竞争,这是主要的市场离散力。
从新经济地理框架开始,空间模型可以证明均衡的存在性和唯一性,但具体的求解主要依赖于计算机运算的数值解。同时,在进行比较静态分析时也往往通过设定具体的参数值求得数值解,从而分析稳态的变化。
然而,新经济地理模型并没有完全解决“空间不可能定理”提出的双重均衡问题。Krugman(1991)的分析思路是先通过市场出清条件得出均衡的要素价格,再讨论该要素价格是否能够实现劳动力的空间均衡,即不同地区的真实工资是否一致①由于该理论框架下企业利润始终为零,因而不存在企业迁移的动机。。劳动力空间均衡的存在性取决于几个核心参数的大小,包括交通成本、同类产品的需求替代弹性和不同行业的消费份额等。一方面,当交通成本足够小时,市场集聚力大于离散力,劳动力将全部集中在某一个或几个位置,而其他位置的劳动力为零。然而,这种情况并不属于本文引言部分定义的空间均衡,也不符合现实观察到的情况,属于一种“黑洞情况”,是一种边角解。另一方面,当交通成本足够大时,市场集聚力小于离散力,劳动力将平均分布在各个位置。虽然这种情况符合劳动力的空间均衡定义,但其无法解释现实中各个位置人口的差异。因此,在空间同质假设下,新经济地理模型虽然能解释集聚的发生,但无法兼顾劳动力的空间均衡和模型的现实解释力。
(四)空间异质、不完全竞争下的量化空间模型
量化空间均衡模型的核心是在同时假设空间异质性和不完全竞争的基础上,进一步引入企业和消费者的异质性,以及空间真实交通网络。其诞生也是更好地适应日益增加的微观经济数据,特别是关于企业和居民的微观调查数据。
在空间模型中引入企业异质性的代表性文献是新新贸易理论。Melitz(2003)和Eaton & Kortum(2002)均假设企业生产率服从某种概率分布,如帕累托和极值分布。引入企业生产率异质性可以讨论要素在不同生产率的企业之间的分配问题,以及分析贸易自由化对企业进入退出的影响(Melitz,2003)。当给定一个具体的概率分布如极值分布,可以进一步建立结构性模型,使用观测的数据估算模型的核心参数,从而基于估计的模型进行反事实分析和福利分析(Eaton&Kortum,2002)。新新贸易理论的研究尺度是国家,因此较少涉及劳动力和资本的跨空间流动的讨论。
如果将新新贸易理论的研究尺度从国家改为城市间或城市内部的区位(location),再加上劳动力或者资本的空间均衡条件,则可以分别演化为量化空间模型中的区域(regional)模型和城市(urban)模型。Redding& Rossi-Hansberg(2017)对量化空间模型的类型、特征和要素进行了非常详细的综述。与新新贸易理论不同的是,量化空间模型还引入了消费者(居民)的异质性,假设消费者对居住或工作在不同地方的偏好服从极值分布。
需要指出的是,另一支使用量化空间模型的文献并没有假设企业生产率或者消费者偏好服从极值分布,而是假设企业采购或者消费者效用函数包含嵌套(nested)的不变替代弹性函数(CES)。例如,Halpern et al.(2015)的企业生产函数中的中间投入品假设是国内和国外产品的CES加总。有意思的是,我们可以从数学上证明这两种不同的假设是互通的,极值分布可以推导出CES函数(具体见Anderson et al.,1992;Mo,2022b)。
量化空间模型与新经济地理模型的核心区别有三点。第一,引入了土地价格作为市场离散力。由于工业用地和商住用地的供给是相对固定的,当人口和企业增加时会推高土地价格,形成重要的反向作用力。第二,引入劳动者的空间均衡,即均衡条件下满足各个区位的期望效用均等化。其隐含的假设是允许每个区位有外生的差异,例如区位的生产率差异和生活便利环境差异。第三,在理论模型中引入现实的复杂交通网络。这个是量化空间模型能够较精确地刻画现实空间数据的核心条件,同时保持模型的可求解性和可处理性(tractability)。
针对“空间不可能定理”的挑战,量化空间模型通过同时假设空间异质和不完全竞争,能够在给定参数条件下实现空间均衡和市场出清的双重均衡,但也意味着其同时面临经典空间均衡模型和新经济地理模型所面临的挑战。一方面,量化空间模型无法解释为什么某些区位的基本面(fundamentals)更优;另一方面,模型均衡解的存在性取决于核心参数的取值范围。当市场集聚力大于离散力时,模型可能不存在(唯一)均衡,退化为非空间均衡的边角解(Allen&Arkolakis,2014)。本文第三节将以量化区域模型为例,详细分析核心参数条件与空间失衡的关系。
(五)空间均衡模型的应用
在经典空间均衡模型的应用方面,范剑勇等(2015)和陆铭等(2015)基于中国特色的土地制度建立适用于中国的劳动力空间均衡模型。他们的基本框架借鉴空间异质下的经典空间均衡模型,引入城市间差异化的土地供应。范剑勇等(2015)发现,高昂房价没有阻止流动人口进入大城市,是因为流动人口主要居住在城中村和厂商集体宿舍等非商住用地的住房。陆铭等(2015)发现,土地指标过多地倾向于中西部,导致东部地区工资和房价过快上涨。范剑勇和莫家伟(2014)利用资本的空间均衡条件,分析地方债务如何通过压低工业用地价格和增加基建投资双渠道吸引资本投资。Mo(2018)使用类似的资本空间均衡条件,分析中国特色的土地制度和土地融资与经济增长的关系。Zhang et al.(2017)基于经典空间均衡模型,构建中国地方政府干预土地供应市场的指标,实证分析地方政府土地市场行为对城市发展的影响。段巍等(2020)基于拓展的Rosen-Roback经典空间均衡模型,量化评估了中国城镇居民在2000至2017年的福利变动并分析其影响因素。赵方和袁超文(2017)在Diamond(2016)关于移民选址的空间均衡模型基础上引入中国的户籍和土地供给等制度性因素,比较分析户籍和流动人口的高、低学历人群的迁移动机差异。
量化区域模型的代表性应用是估算交通基础设施和其他影响迁移成本的政策对整体福利的影响。由于交通网络对各个区域既有直接影响,也有间接影响,一般线性回归无法估计出一般均衡下的福利总效应。量化区域模型能把交通网络的直接和间接影响囊括在内。Donaldson&Hornbeck(2016)建立区域间的量化一般均衡模型,构建县的市场通达性指标(market access),发现美国在1870至1890年间的铁路网扩张显著提高了县的市场通达度并提高了农业土地价值。进一步的反事实分析指出,如果去掉美国的铁路网,土地总值会下降60%,人口规模和消费者总福利也会大幅度下降。Allen & Arkolakis(2019)针对交通网络建立了更为精确的区域一般均衡模型分析交通基础设施投资的福利效应。他们发现美国的高速公路网显著提高了整体的福利水平,同时也发现了各个地区的异质性福利效应,其中大都市区和重要的贸易节点受益最大。关于中国的应用,Tombe&Zhu(2019)构建包含中国户籍迁移成本的量化区域模型,发现贸易和迁移成本的下降能够解释中国在2000—2005年间总体劳动生产率提升的36%,其中国内的贸易和迁移成本下降的影响大于国际贸易的成本下降。值得一提的是,他们的模型将国际和国内商品贸易以及国内劳动力流动同时考虑在内,集合了Eaton & Kortum(2002),Krugman(1991)和Ahlfeldt et al.(2015)等模型的核心要素。赵扶扬和陈斌开(2021)在上述量化区域模型基础上引入中国的土地和财政制度性因素,对中国土地的区域间配置进行量化分析和评估,发现现实中的土地配置较好地平衡了“效率”与“公平”,在实现GDP提升的同时缩小区域间人均收入差距。
量化城市模型的代表性应用是估计城市内部的集聚效应。在实证上估算城市的集聚效应的最大挑战在于无法区分不同区位本身固有特征和其集聚效应。在理论上的挑战是,一般的城市模型假设单中心或者对称模型,无法体现不同区位固有的差异。Ahlfeldt et al.(2015)在居民通勤选址偏好中引入随机冲击,借鉴Eaton&Kortum(2002)的极值分布,建立了量化城市均衡模型,推导出市内通勤的引力方程。作者利用柏林墙建立和推倒的自然实验,结构化地估计生产地和居住地的外部性参数,发现集聚效应能够解释很大一部分城市结构的变化,证明了城市经济密度(density)的重要性。Heblich et al.(2020)构建类似的量化城市模型,分析伦敦在1801—1921年间的蒸汽铁路网对城市发展的影响。反事实分析发现,假如去掉当时的整个铁路网,大伦敦地区的人口和土地价值会下降20%或更多,同时往伦敦城通勤的人口会从37万下降到6万。关于中国城市的应用,Mo(2022a)建立适合中国土地利用制度的量化城市模型,分析城市内部交通设施如何影响城市居民的分布。基于厦门的集美、杏林大桥和翔安隧道的修建事件,Mo(2022a)发现两座新大桥使得市中心人口更分散,而翔安隧道的通车却使得市中心人口更集中。进一步分析发现,基建对人口分布的异质性效果的原因在于,基建周围的公共设施分布和企业生产率分布存在显著差异。翔安隧道连接的外围区域缺乏较好的公共服务设施,如优质中小学,故居民不愿意迁移隧道连接的外围区域。
总体而言,空间均衡模型在中国的应用偏重于分析具有中国特色的空间管理政策对经济发展和社会福利的影响,隐含的前提假设是现实满足空间均衡和市场出清双重均衡存在的条件。
三、空间经济理论的挑战:以量化区域模型为例
空间经济理论在应用中面临的核心挑战是,现实中我们难以观测或推断空间上的市场集聚力与市场离散力的相对大小。当空间上的市场集聚力显著大于市场离散力时,人口的空间分布会趋向于失衡状态,个别区域可能形成“黑洞”情况,即理论上的边角解。虽然在理论上可以依据模型设定和参数大小判断是否有空间均衡,但是在应用空间经济模型的时候,我们往往假设现实数据是理论上的某个均衡状态,然后根据数据反估模型参数。这在逻辑上可能存在问题,因为现实数据可能处于某种失衡过程中,由此反估的参数即使符合理论要求的存在空间均衡的参数条件,也无法证明现实数据是反映空间均衡状态。
为什么我们难以判断空间上的市场集聚力与市场离散力的相对大小?不同的理论假设下空间均衡的存在性和唯一性所要求的参数条件可能差异非常大,而现实中我们难以知道哪种理论假设符合真实情况,因此估计出来的参数无法帮助我们判断空间均衡的存在性。
为了更好地说明不同理论假设下空间均衡的存在性和唯一性的参数条件的差异,我们以量化区域模型为例,比较两种理论假设下的参数条件。一种是假设完全竞争市场,每个城市只有一个代表性厂商,价格等于当地边际成本。另一种是假设垄断竞争市场,每个城市有多个厂商,价格包含成本加成,不同企业的产品属于不同样式(variety)。我们会证明,两种不同假设下,空间均衡的存在性和唯一性所要求的参数条件恰好相反。
(一)完全竞争下的量化区域模型
我们首先分析完全竞争市场下的模型结构。假设城市内部各个厂商的技术相同,产品样式相同,厂商生产率由所在城市的平均生产率决定,商品价格等于生产的边际成本。
(1)消费品的城市间网络效应
消费者在城市i的效用函数由以下几个部分构成:
i.城市i的宜居度Bi。宜居度在数据上可观测的主要包括城市的公共服务如优质学校和医院的数量,以及城市的气候(温度、湿度、降水)和空气污染(PM2.5)。
ii.消费篮子Xi。假设每个城市生产的产品有差异,消费篮子包括所有城市的最终产品,通过CES函数加总。由于运输成本的存在,城市i与各个城市之间的交通距离会影响消费篮子的各个产品的选择比例。可以证明,交通通达性越好的城市,平均物价水平越低,消费者效用越高。
iii.住房面积hi。基于常规假设,工资越高且房价越低时,住房面积越大,效用越高。
因此,消费者在城市i的效用函数为:

消费篮子Xi是各地最终产品的CES加总:
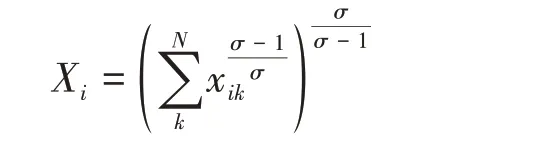
其中,N是城市数量,k是第k个城市,xik是i城市消费者对k城市产品的消费量,0<α<1是消费占收入的比例,σ>1是消费品的替代弹性。预算约束是pkxik+rihi=zi,其中τik>=1是从城市k到城市i的运输成本,假设为冰山成本;pk是城市k的产品的FOB价格;zi是居民收入。
根据效用最大化可以求得,消费者在城市i的间接效用为:
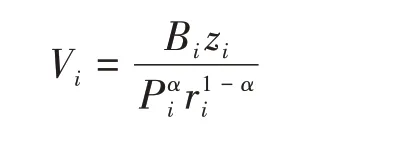
其中,Pi是消费品物价指数,等于各个城市加上运输价格后的最终品价格的CES加总,即:

城市i的物价指数反应了城市的交通通达性。当连接城市i的交通设施降低运输成本时,该城市的物价水平将下降,从而提高了迁移到该城市的效用。
(2)企业的定价决策
我们假设每个城市有一个代表性企业,按照边际成本定价。企业在城市i的生产函数由以下两个部分构成:
i.城市i的生产率Ai。生产率在数据上可用全要素生产率(TFP)作为衡量,也可使用微观企业的平均劳动生产率。
ii.劳动力投入数量Li。
假设企业在城市i的生产函数是简单的线性形式:
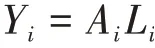
基于完全竞争市场的假设,企业的经济利润为零,由此得城市i的产品价格为:
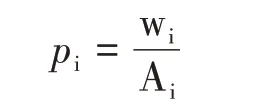
其中,wi是名义工资,城市的工资越低,生产率越高,则该城市的产品越有竞争力。
(3)均衡房价
假设城市i的土地供给Hi为外生给定。根据房屋总需求面积等于总供给,可以求得城市i的均衡房价为:
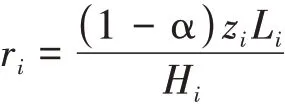
为了简化模型的讨论,这里假设住房收入全部返还给当地居民,即有ziLi=wiLi+riHi,从而得到个人收入与工资之间的关系为zi=
(4)城市间贸易份额
根据消费篮子的CES函数的优化条件并结合企业定价公式,可得城市i的消费者购买城市k的产品的份额为:
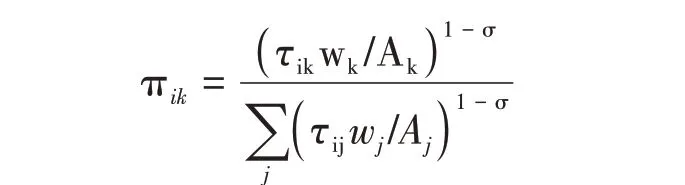
当k城市的工资越低、生产率越高,且离i城市的距离越近时,城市i从城市k购买的份额将越大。基于贸易份额表达式,价格指数可以简化为:

(5)空间均衡
假设劳动力在不同城市间自由流动,空间均衡条件是每个城市的效用达到一致。结合均衡房价、收入和企业定价条件,即有:
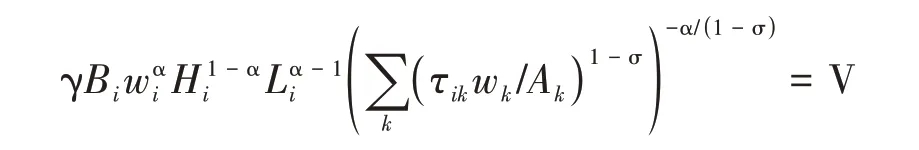
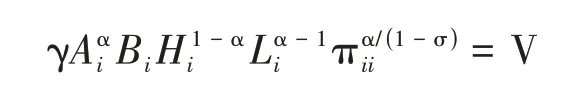
(6)市场出清
商品市场出清要求所有城市的消费者购买城市i的产品的总支出等于城市i的企业的总收入:
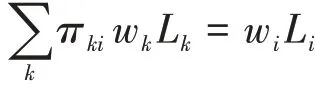
最后,劳动力市场出清为:

(7)空间均衡的存在性和唯一性条件
将贸易份额、空间均衡条件代入商品市场出清条件,整理得:


根据交通成本的对称性τki=τik,综合上述两式可以得到:

其中Ф是一个调整的常数。由此得到关于工资和人口的一一对应关系。将其代入上述价格指数公式,替代人口变量,得到关于工资的特征函数(eigenfunction)如下:
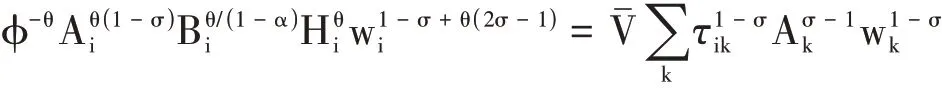
根据Allen & Arkolakis(2014),当等式两边的工资变量对应的指数参数(即1-σ+θ(2σ-1)和1-σ)的比值符合特定区间,即时,化简得1∕σ>1-α,该特征函数存在唯一的解。Allen et al.(2020)系统地考察了一系列量化空间模型的解的存在性和唯一性条件,发现模型解的唯一性的核心是需求和供给弹性。Redding&Rossi-Hansberg(2017)也给出了类似模型的解的唯一性条件。
该唯一性条件的经济含义是,在完全竞争市场下,市场集聚力主要来自于消费者对不同地区产品的偏好多样性,σ越小,代表多样性偏好越强,由此形成的消费网络的集聚力越强。另一方面,市场的离散力来自于房价,当房子占消费比例越大,即1-α越大时,离散力越大。完全竞争市场由于缺乏本地市场的规模效应,因此源自多样性偏好的集聚力必须足够大于离散力才存在空间唯一均衡解。
(二)垄断竞争下的量化区域模型
垄断竞争假设与完全竞争假设的核心区别包括两部分。第一,每个城市不是一个代表性企业,而是有Mi个企业,企业数量是内生的,每个企业代表一个样式。假设消费者先选择每个城市最优的产品消费组合,然后再选择所有城市的总消费组合。第二,企业生产函数引入固定成本,在自由进入退出条件下,固定成本等于垄断利润。
我们将消费篮子Xi拓展为嵌套的CES加总函数:

其中,N是城市数量,k是第k个城市,j是城市k的企业j的产品,Mk是城市k的产品种类数量(或企业数量),xikj是i城市消费者购买k城市的j产品的数量。σ>1是不同种类消费品的替代弹性。预算约束是。其他符号与完全竞争模型一致。
消费品物价指数Pi拓展为:

假设城市i的企业j的生产函数为:
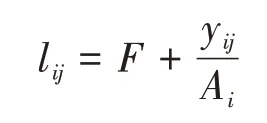
其中,lij是劳动投入,F是固定成本,假设所有城市所有企业都一样,yij是产量,Ai是生产率,假设企业的生产率等于所在城市的平均生产率水平。
值得一提的是,我们也可以假设城市内部的企业生产率服从某个包含城市特定生产率参数的极值分布,然后消费者从每个城市选择价格最低的那个企业。我们可以证明这种设定与本模型的设定本质是一致的(Anderson et al.,1992;Mo,2022b)。
根据利润最大化条件可以得到企业的定价决策:

同一个城市的所有企业价格相同,即边际成本乘以固定的成本加成。结合零利润条件,得到企业产量为yij=AiF(σ-1),劳动投入为lij=σF。城市i的企业(产品种类)数量为:

从企业数量可以看出,一个城市人口规模越大,能享受的产品种类越多,综合物价越低。消费品物价指数可以化简为:

垄断竞争模型与完全竞争模型的核心差别是,此处价格指数包含了各个城市的人口规模作为权重,由此产生本地市场的规模效应。消费者在选择城市消费比例的时候将更倾向于选择大城市的产品。
最后,贸易份额表达式为:

其他关于房价均衡、空间均衡、商品市场和劳动力市场出清等条件均与完全竞争模型一致。空间均衡条件整理为:

将拓展的贸易份额、空间均衡条件代入商品市场出清条件,整理得:


根据交通成本的对称性τki=τik,综合上述两式可以得到:

其中Ф是一个调整的常数。由此得到关于工资和人口的关系,将其代入整理好的上述价格指数公式,得到关于工资的特征函数(eigenfunction):

我们还可以整理为关于城市人口的特征函数:
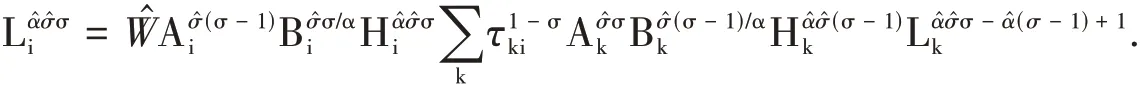
根据Allen & Arkolakis(2014),当时,简化得1∕σ≤1-α时,该特征函数存在唯一的解。
(三)两种市场假设下空间均衡参数条件的比较
比较完全竞争和垄断竞争下的模型解的唯一性条件,不难发现,两者对核心参数的取值要求恰好相反。完全竞争市场下,解的存在性和唯一性条件是1∕σ>1-α,而垄断竞争市场下的条件是1∕σ≤1-α。
上述两种市场假设中,共同包含的市场集聚力是来自不同城市的产品多样性偏好带来的消费网络的集聚力,由城市间的交通成本矩阵驱动,当σ越小(即1∕σ越大),这种集聚力越强;共同包含的市场离散力是来自房价的阻碍力,当房屋消费占总消费比例越大,即1-α越大时,离散力越大。
然而,垄断竞争的设定比完全竞争设定包含多一层市场集聚力,即本地人口越多,内生的企业数量越多,从而降低价格指数和提高消费者效用,进一步吸引更多的人口流入。由于多了这一层市场集聚力,为了保持总体集聚力与离散力的相对平衡,需要提高房价的离散力(1-α)以实现空间平衡,所以参数上要求1-α≥1∕σ。对应地,由于完全竞争下缺少这一层集聚力,要维持总体集聚力与离散力的相对平衡,反而需要降低房价的离散力,故参数上要求1-α<1∕σ。
总结起来,量化空间模型的均衡解的存在性和唯一性取决于多种市场集聚力和离散力的相对平衡。不同的市场竞争假设本身会产生不同的空间集聚力,对应的空间均衡存在性和唯一性参数条件也截然不同。因此,在现实应用中,我们面临的问题是不知道现实更符合哪种市场竞争假设,由现实数据估计得到的参数(例如σ和α)也无法知道适用于何种模型。
空间经济理论面临的挑战从本质上仍然是“不可能定理”揭示的价格机制的“一石不能打二鸟”的问题。仅依靠市场机制,我们可能难以保证市场的各种集聚力和离散力的相对平衡。当这两种对立的力量失去平衡,生产要素的空间分布将趋向于两种极端。当市场集聚力大于离散力,人口和企业的流动将趋向于集中在单一位置,形成空间上的极端不平等和城市的极端拥堵。另一方面,当市场集聚力小于离散力,人口和企业的流动将趋向于极端分散和自给自足,经济将失去规模效应和集聚收益。
根据第七次全国人口普查,我国的人口空间分布呈现出进一步集聚的趋势,近十年人口向东南沿海省市和区域内中心城市进一步集聚。假如市场集聚力持续大于市场离散力,导致人口空间分布的持续不稳定,那么政府可以采取增强非中心城市的人口吸引力、提高非中心城市的教育、医疗资源以及匹配当地经济禀赋的招商引资等措施维持两种力量的相对平衡。值得一提的是,中共中央办公厅、国务院办公厅印发的《关于推进以县城为重要载体的城镇化建设的意见》涉及人口的空间分布,是重要的政府空间政策管理。本文认为,在空间失衡状况下,政府可以通过实施多种类型的空间政策,适当增强离散力或者增强集聚力以维持两种空间力量的相对平衡,从而更好地实现劳动力和企业的空间均衡,维持经济稳定发展,提升整体社会福利。
四、小结
本文针对市场价格机制提出了一个基本的问题:价格机制是否能够同时实现供需平衡和空间均衡?不同于市场供需平衡,空间均衡是一个相对较少被关注的均衡概念。其定义是居民或企业在不同地方的效用或利润相等,不存在迁移的动机。空间均衡的存在性是分析人口的最优空间分布的重要前提。假如价格机制无法实现劳动力的空间均衡,经济体陷入空间失衡情况,那么城市人口规模将始终处于非稳定状态,这会给城市房价埋下不稳定的种子,并有可能引发经济和金融风险。
为了回答这个问题,本文从最基本的“空间不可能定理”出发,指出在完美情况下(空间同质和完全竞争),交通成本的存在将使得价格机制无法实现空间均衡。其根本原因在于,价格系统在支撑区域间的商品和要素贸易时所传递的信号,恰好会提供劳动力和企业进行空间迁移的动机。围绕“空间不可能定理”相关假设条件,本文将空间均衡理论的发展归纳为三个方向:引入空间异质性的经典空间均衡模型、引入垄断竞争的新经济地理模型,以及同时引入空间异质性和垄断竞争的量化空间模型。本文指出,这三类模型均无法保证价格机制能够实现空间均衡。
本文进一步以量化区域模型为例,指出空间均衡的核心条件是需要多种市场集聚力和离散力维持相对平衡。当市场集聚力显著大于离散力时,经济体有可能陷入空间失衡状况,形成空间“黑洞”情况。政府在这个情况下,可以通过实施适当的空间政策调整集聚力和离散力,以维持空间层面的经济稳定。
总结起来,单靠市场价格机制或者政府政策都无法保证实现市场和空间的双重均衡。只有根据具体国情,恰当地结合市场机制和政府的空间政策,才能更好地实现空间均衡,并在此基础上寻找最优的经济空间分布,以实现社会福利最大化。

