高覆盖摄像机辅助的室内可见光定位算法

贾松霖，刘俊伟，胡吴瑕，金 玲

(1.航天东方红卫星有限公司，北京 100094； 2.北京邮电大学 a.世纪学院; b.信息与通信工程学院,北京 100086)

0 引 言

可见光定位(Visible Light Position，VLP)技术因低成本和高精度的特点而受到越来越多的关注[1]。许多VLP算法已经被提出，包括近邻法[2]、指纹法[3]、三边定位法[4-5]和图像传感器法[6]。在这些算法中，近邻法是最简单的，但其对发光二极管(Light Emitting Diode, LED)的密度要求高，因此定位精度较低；指纹法可实现较高的定位精度，但需要较高的成本建立数据库；相比之下，基于接收信号强度(Received Signal Strength，RSS)的三边定位法和图像传感器法因其高精度和低成本的特点成为两种最有潜力的定位算法[7]。

然而，基于RSS的三边定位法和图像传感器法也存在着各自的挑战。一方面，基于RSS的三边定位法难以实现高的覆盖范围。在实际应用中，光电二极管(Photo Diode，PD)的方向是随机且未知的，这限制了RSS法的覆盖范围及应用。另一方面，透视n点(Perspective-n-Point，PnP)算法是一种典型的图像传感器算法，其成本低且不限制摄像机方向，然而，PnP法至少需要4个LED才能获得确定的位置。在文献[7]中，作者提出了一种增强型摄像机辅助的接收信号强度比(Enhanced Camera Assisted Received Signal Strength Ratio，eCA-RSSR)算法来解决RSS和PnP法的问题。但eCA-RSSR算法的定位精度会随着LED间距的减小而下降。因此，需要提出一种在图像噪声下能够实现高精度和高覆盖的定位算法。

本文提出了一种新颖的非线性摄像机辅助的接收信号强度(Non-linear Camera Assisted-Received Signal Strength，nCA-RSS)算法，该算法在图像噪声下可以实现高覆盖和高精度定位。

1 系统模型

本文所提定位系统如图1所示。VLP系统中有4个坐标系，分别是三维(3-Dimensional，3D)世界坐标系(World Coordinate System，WCS)Ow-xwywzw、3D摄像机坐标系(Camera Coordinate System，CCS)Oc-xcyczc、图像平面上的二维(2-Dimensional，2D)图像坐标系(Image Coordinate System，ICS)Oi-xiyi和图像平面上的2D像素坐标系(Pixel Coordinate System，PCS)Op-upvp。在PCS、ICS和CCS中，坐标轴up、xi和xc相互平行，类似地,vp、yi和yc也相互平行。Op位于图像平面的左上角，Oi位于图像平面的中心，称为主点，其像素坐标为(u0,v0)T。Oc为摄像机的光学中心，Oi位于光轴上。由于焦距f是Oc和Oi之间的距离，因此在CCS中图像平面z的坐标为zc=f。此外，第i个LED、第i个LED在图像平面上的投影和Oc在同一条直线上。

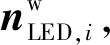
假设LED遵循朗伯辐射模式。由于视距链路是光信道的主要组成部分，因此为了简化，本文只考虑该链路[1]。第i个LED与PD之间的信道直流增益可表示为

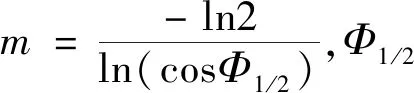
图1 VLP定位系统Figure 1 Visible light positioning system

式中：n为聚光器的折射率；Ψc为PD的视场角(Field of View，FoV)。令Pt为每个LED的发射光功率，则从第i个LED接收到的光功率Pr,i可表示为

式中：Hi为不同LED到接收端的信道系数。

将式(1)代入式(3),Pr,i可改写为

PD接收到的光功率Pr,i可通过电流Ir,i=Pr,iRp来测得，Rp为光/电转换效率。

典型的VLC系统噪声包括散粒噪声和热噪声，可以被建模为加性高斯白噪声(Additive White Gaussian Noise，AWGN)。因此，信噪比(Signal-to-Noise Ratio，SNR)为

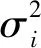
2 nCA-RSS算法

在本节中，提出了一个两步算法—nCA-RSS算法。在第1步中，基于单视图几何理论，入射角可以通过摄像机捕获的视觉信息来估计；在第2步中，基于莱文贝格—马夸特(Levenberg-Marquardt，LM)算法，接收器位置可以通过PD收到的RSS来获得。

2.1 入射角估计

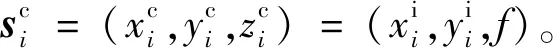
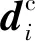
式中，oc=(0c,0c,0c)为摄像机坐标的原点。因此，第i个LED对应估计的入射角ψi,est为

2.2 位置估计

第i个LED对应辐照角的余弦为

将式(9)代入式(4)可得：

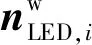
并更新为

WhileK=3 do

fori=1→Kdo

根据式(8)和(9)计算出ψi,est和cos(φi)；

在未知的rw下更新Pr,i；

end for

end while.

2.3 nCA-RSS算法的实现

在发射端，3个LED提供照明和位置信息。为了避免LED之间的干扰，VLP系统可以利用时分复用技术来识别每个LED的信号功率。每个发射器由一个封装单元、一个编码器、一个调制器和一个LED组成。封装单元用于创建数据帧，其中包含帧首定界符和发射器的身份信息。然后，为了避免闪烁问题，可以采用曼彻斯特编码将‘0’转换为‘01’，‘1’转换为‘10’。最后，数据帧通过开关键控(On-Off Keying，OOK)进行调制。经过调制后，发射器的身份信息可以通过LED进行广播。

在接收端，可以使用带有前置PD和前置互补金属氧化物半导体摄像机的设备，例如智能手机和平板电脑。一方面，通过摄像机标定可以得到内参矩阵和畸变参数，从而建立PCS和CCS之间的关系。然后，通过设置适当的曝光来捕获发射器。一旦获得图像，就可以利用图像处理来获得LED投影的像素坐标。经过解调和解码后，利用包同步在接收到的比特流中检测同步码。通过这种方式可以获得LED的身份信息。一旦确定了LED的像素坐标和身份信息，就可以计算出可见光的入射角。另一方面，PD包含一个可变增益的跨阻放大器，在每个时隙能够接收到每个LED的信息，并将入射光子转换为电子/电流。然后，将示波器连接到PD来提取RSS。同时，利用模/数转换器对模拟信号进行采样来获得离散比特。经过解调、解码和包同步后，即可确定LED的身份信息。这样，经过3个时隙就可以得到3个LED的RSS和身份信息。最后基于入射角和RSS，利用LM算法来获得接收器的位置。

3 仿真结果与分析

在本节中，将使用PnP、RSS和eCA-RSSR算法作为比较方案，其中PnP法只利用了视觉信息，RSS法只利用了信号强度信息，eCA-RSSR算法使用了视觉和信号强度信息。为了在同一场景中比较本文所提算法和比较方案，仿真中考虑了典型的4个LED布局。

系统参数如表1所示。为了在接收端获得LED的世界坐标，本文假设可见光信号经过OOK调制。所有统计结果都经过了1 000次独立运行。对于每次仿真运行，从接收器可以检测到足够LED进行定位的区域中随机选择测试位置。为了减少由信道噪声引起的误差，接收光功率使用1 000次测量的平均值。针孔摄像机已校准完毕。图像噪声被建模为高斯白噪声，期望为0，标准差为2.5个像素。由于图像噪声会影响图像平面上LED投影的像素坐标，因此LED投影的像素坐标是通过处理相同位置的10张图像来获得的。

表1 系统参数Table 1 System parameters

我们比较了nCA-RSS、eCA-RSSR、PnP和RSS算法的精度和覆盖范围。定位误差(Positioning Error，PE)用于评估定位算法的精度，定义如下

式中：Neffective为接收器可以检测到足够LED进行定位的位置数量；Ntotal为测试位置的总数。

表2所示为nCA-RSS、eCA-RSSR、PnP和RSS算法进行3D定位所需的LED数量。此外，nCA-RSS、eCA-RSSR和PnP算法都可不受接收器方向的影响来进行定位。然而，RSS法在没有额外传感器的帮助时需要固定接收器方向，通常RSS法要求PD垂直向上朝向天花板。图2评估了nCA-RSS、eCA-RSSR、PnP和RSS算法的3D CR性能，图中FoVΨc从0变化到80 °。样本沿房间的长宽高选择定位点，彼此相距10 cm。为了确保可靠的OOK传输，SNR值不应小于13.6 dB[5]。如图2所示，与eCA-RSSR算法相同，nCA-RSS算法对所有Ψc都实现了最高的CR。具体来讲，Ψc从20到80 °，nCA-RSS算法的CR都能够超过80%，比PnP和RSS算法分别高5%和50%左右。同时，Ψc从5到20 °，nCA-RSS算法的CR从0迅速增加到80%。相比之下，对于Ψc≤10 °的情况，PnP和RSS算法几乎是无法定位的。

表2 定位方案所需的LED数量Table 2 The number of LEDs needed for different positioning schemes

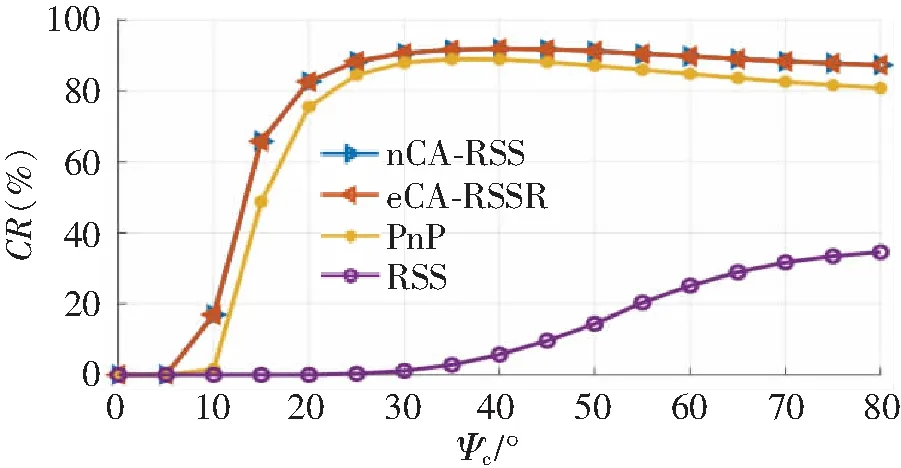
图2 nCA-RSS、eCA-RSSR、PnP和RSS算法的3D CR性能Figure 2 3D CR performances of nCA-RSS, eCA-RSSR, PnP and RSS algorithms

图3所示为接收器方向对nCA-RSS、eCA-RSSR、PnP和RSS算法3D定位精度的影响。假设接收器有一个预设的倾角θ和一个随机的角度扰动δ。在比较方案中，RSS法的高精度定位依赖于接收器方向的准确估计，这在实际应用中具有一定的挑战性。因此，RSS 法考虑了两种情况：理想情况下RSS法可以获得准确的接收器倾角θ±δ，而非理想情况下无法测量δ。相比之下，nCA-RSS、eCA-RSSR 和PnP算法不受接收器方向的限制，因此不分情况考虑。仿真中θ是可以变的，而δ服从[0,5]的均匀分布。精度性能由PE的累积分布函数(Cumulative Distribution Function，CDF)表示。如图所示，nCA-RSS算法可以达到4种算法中的最佳性能。具体来讲，nCA-RSS算法对于80%以上的样本可以实现2.5 cm的定位精度，比PnP、eCA-RSSR和RSS算法低1.0、2.5和6.5 cm。此外，理想情况下的RSS法可以获得比nCA-RSS算法略低的PE。这是因为,理想情况下的RSS算法利用了理想的方向估计，这在实际应用中是不可行的。

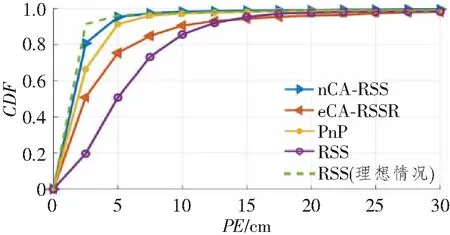
图3 接收器方向对nCA-RSS、eCA-RSSR、PnP和RSS算法的3D定位精度的影响Figure 3 Influences of different directions of receivers on the 3D positioning accuracy of nCA-RSS、eCA-RSSR、PnP and RSS algorithms

图4所示为沿x、y和z轴下接收器方向对nCA-RSS、eCA-RSSR、PnP和RSS 算法的3D定位精度的影响。如图所示，沿x、y、和z轴nCA-RSS算法和理想情况下的RSS算法实现了4种算法中的最佳性能。然而，即使利用陀螺仪去估计接收器方向也有偏差，理想情况下的RSS算法在实际应用中可能过于理想化。相比之下，本文所提nCA-RSS算法能够在没有完美方向估计的假设下实现最佳性能。

图4 沿x、y、和z轴接收器方向对nCA-RSS、eCA-RSSR、PnP和RSS 算法的3D定位精度的影响Figure 4 Influences of different directions of receivers along x, y and z on the 3D positioning accuracy of nCA-RSS、eCA-RSSR、PnP and RSS algorithms

图5所示为nCA-RSS、eCA-RSSR和PnP算法在图像噪声影响下的平均PE，其中图像噪声被建模为期望为0且标准差为0～5个像素的高斯白噪声。由图可知，本文所提nCA-RSS算法对图像噪声不敏感。nCA-RSS算法的平均PE为2.5 cm，是3种算法中最低的。此外，随着图像噪声的增加，nCA-RSS算法的平均PE保持不变。相比之下，eCA-RSSR算法的平均PE从4.0增大到6.5 cm。PnP法的平均PE从0增大到10.5 cm。这是因为,在入射角估计完成后，nCA-RSS算法仅利用信号强度信息去定位。相比之下，eCA-RSSR和PnP算法更依赖于视觉信息，因此对图像噪声更敏感。

图5 nCA-RSS、eCA-RSSR和PnP算法在图像噪声影响下的平均PEFigure 5 Average PE of nCA-RSS,eCA-RSSR and PnP algorithms under the influence of image noise

图6所示为PD和摄像机之间的距离dpc对nCA-RSS算法 3D定位精度的影响。如图所示，给定dpc=0、1、3、6和10 cm，nCA-RSS算法可达到约15 cm的80%精度，并且PE随着dpc的增加而增加。当dpc= 1 cm时，定位精度与dpc=0 cm时相同，因此dpc的影响几乎可以忽略不计。这里，dpc=0 cm意味着PD和摄像机的位置重叠，这在实际中是不可能的。值得注意的是，dpc=1 cm是智能手机上的典型配置(例如苹果iPhone XS中dpc<1 cm)。因此，所提出的 nCA-RSS 算法特别适用于尺寸相对较小的设备。

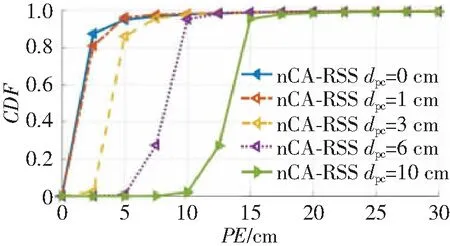
图6 PD和摄像机之间的距离对nCA-RSS算法3D定位精度的影响Figure 6 Influence of the distance between PD and camera on the positioning accuracy of nCA-RSS algorithm

4 结束语

本文提出了一种名为nCA-RSS算法的新型室内定位算法，其同时利用了可见光的视觉和强度信息。与传统的RSS算法相比，nCA-RSS算法可以消除接收器方向的限制，实现更高的覆盖性能。与传统的PnP算法相比，nCA-RSS算法可以使用更少的LED实现更高的精度。与 eCA-RSSR算法相比，nCA-RSS算法可以获得更准确的带有图像噪声的位置估计。仿真结果表明，无论接收器方向如何，nCA-RSS算法对于80%以上的样本可以实现约2.5 cm的定位精度。因此，nCA-RSS算法是一种很有前景的室内VLP方法，可以实现高精度、高覆盖和广泛的应用。