质子交换膜燃料电池氢循环喷射器的组分输运与相变研究＊

孙文慧，梁丽华

(山东建筑大学信息与电气工程学院，山东 济南 250101)

0 引言

汽车的普及和发展一直伴随着石油消费危机和空气污染危机。质子交换膜燃料电池以氢为燃料，具有零污染物排放、启动速度快、工作温度低、结构紧凑等特点，是替代内燃机(ICE)最有前景的技术[1]。

喷射器因结构简单、无运动部件、无寄生功率等特点正逐渐取代传统的机械泵，回收利用未消耗的氢气和水蒸气，提高PEMFC 系统的性能，成为近年来的研究热点[2]。PEMFC 阳极侧氢罐中释放的氢气作为高压一次流，进入喷射器，引射循环回路中未消耗的氢气和未排尽的水蒸气；流体在喷射器中混合，作为燃料输送到电堆。喷射器需充分回收未消耗的氢，及时排出产生的液体水。

迄今为止，对PEMFC系统阳极氢气再循环喷射器的研究数量有限，主要集中在利用CFD 方法进行机理研究和优化。Feiqiang Li.[3]等考虑吸入流体中水蒸气质量分数，设计了一种具有汇聚喷嘴和圆柱形混合管的喷射器，在PEMFC 系统内达到预期的摩尔再循环比。文献[4]基于剪切应力等输运模型，建立了喷射器二维轴对称模型，结果表明，二次流湿度和混合室直径对氢气再循环率有显著影响。由上述文章可知，喷射器阳极氢气再循环中，二次流湿度在20%～100%左右，且由多种气体组成，必然会对喷射器性能产生影响。

不同工况下复杂的内部流动结构对喷射器性能有很大的影响，成为近十年来喷射器研究的主要课题。Croquer[5]基于热力学双方程湍流模型，观察激波列沿线的高压和低压区域。文献[6]显示在冲击波和边界层处出现了最大流速约1.8 马赫，伴随着清晰的、明显的压力变化。同时，喷射器内复杂的超声速流体动力学、压力变化、高湍流等使得蒸汽凝结和相变的现象受到越来越多的重视[7]。Wang等[8,9]采用湿蒸汽模型研究了过热蒸汽液位对喷射器内冷凝液滴半径、液滴数量、液分数和引射性能的影响，完成了喷射器的结构设计。

多篇文章针对一次流和二次流均为水蒸气的工况，对喷射器内的凝结和相变进行了研究[7-9]。然而，在PEMFC 系统中，喷射器的一次流是氢气，而二次流是氢气和水蒸气的混合物。喷射器内工作流体的变化会引起气体粘度、密度等热机械参数的变化，这些变化对冷凝现象有重要影响。此外，之前文献研究的喷射器内冷凝过程几乎发生在制冷和MED-TVC 系统中，二次流和出口流体相互独立。相反，在PEMFC系统中，二次流和出口流体的参数是强耦合的。

本研究的主要贡献在于：建立了一种组分输运-相变模型，并将其应用于PEMFC 系统中阳极再循环喷射器的流动动力学特性分析和操作性能评价。

1 喷射器模型

用于PEMFC 系统阳极再循环的喷射器由五部分组成，如图1 所示：喷嘴、吸入室、混合室、等面积段和扩散段。一次流氢气在收敛喷嘴内扩大速度，降低压力。由于压差，吸入室内超音速氢气损失部分动能，由二次流入口吸入未消耗的氢气和水蒸汽。两种流体在混合室中混合，进行复杂的能量交换，在等面积段和扩散段发生剪切混合，具有一定湿度和压力(背压)的混合流体在出口处被送到燃料电池电堆。

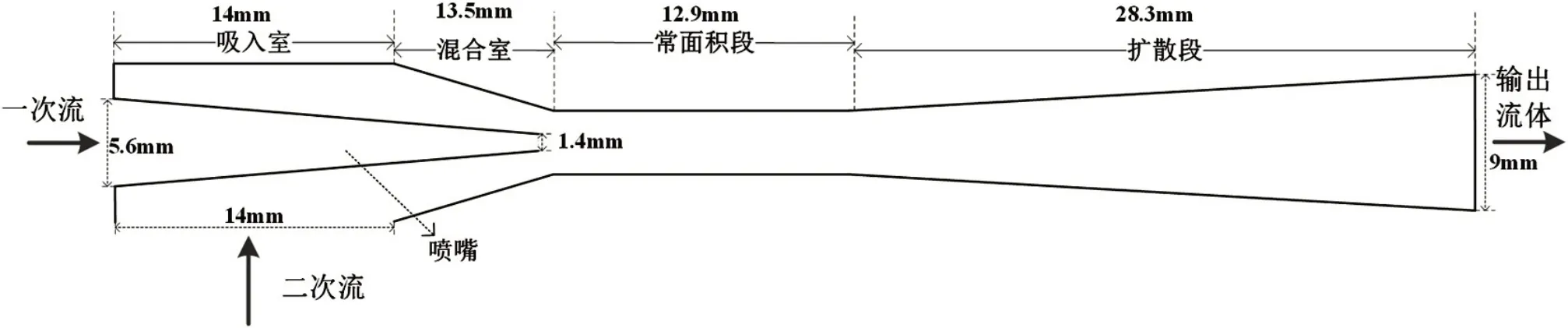
图1 PEMFC系统阳极再循环喷射器结构图

为了研究喷射器内流体动力学特性，本文提出组分输运-相变模型，控制方程由质量、动量和能量守恒方程来描述。为了模拟多相流体动力学，可以采用Mixture模型求解混合相的动量、连续性和能量。由此得到各相体积分数、各组分质量分数和相对速度的代数表示。

⑴在混合物模型中，连续性方程，即二维轴对称结构的质量守恒方程，由式⑴得到：

其中，ρm为混合物的密度，∇为标量的梯度或矢量的梯度(二阶张量)为混合物的平均质量流量。

考虑组分输运，利用对流扩散质量守恒方程式⑵预测各组分的局部质量分数：

其中，ρ是混合物密度，mj是第j个组分质量分数是第j个组分由于浓度和温度梯度的扩散通量，Rj是化学反应生成速率，Sj是用户定义的反应生成速率。

对于第k相，求解对流扩散方程(3)来预测各组分的局部质量分数。

其中，αk为第k相的体积分数，mjk为第k相中第j组分的质量分数为第k相的质量流量，mki→pj为第k相到第p相中第i组分和第j组分之间的质量传输。

将各相的动量方程求和，得到动量守恒方程，由公式⑷给出：

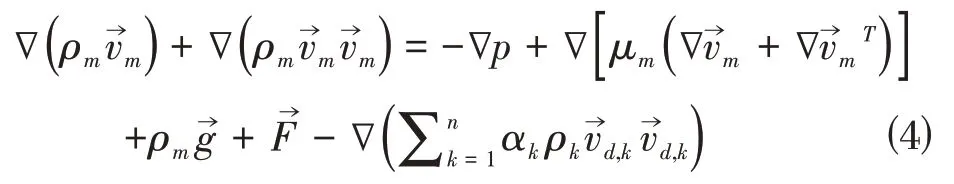
其中，n为相的个数，μm为混合物粘度为外部体积力为重力体积力。

能量守恒方程定义为式⑸：

2 计算流程

2.1 边界条件

根据电堆输出功率和运行状态调整喷射器的工作参数。本研究根据中国弗尔赛能源公司设计的RDZ04 系列PEMFC 的实际运行工况进行参数的设置，电堆输出功率为40kW～70kW，喷射器运行参数如表1所示。

表1 PEMFC系统内喷射器运行工况

2.2 数值计算过程

利用CFD 预处理软件GAMBIT GUI 将喷射器的几何形状划分为若干规则区域，生成网格。基本物理模型、湍流模型、多相流模型、部件输运模型和求解器均使用流行的商用CFD 软件包Fluent 18.0 实现。采用Besagni 讨论的与实验数据吻合较好的RNG k-ω模型，考虑湍流旋涡的低雷诺数流动的黏度。

考虑液体流动连续性的特点，多相模型采用欧拉-欧拉模型求解混合相的动量、连续性和能量方程、二次相的体积分数方程以及相对速度的代数表示。组分输运模型选择混合物物料，考虑各组分的质量分数，确定混合物的密度、比热、导热系数和粘度等物理性质。

3 实验结果

图2 为基于组分输运-相变模型和干蒸汽模型预测的喷射器内部压力分布图。一次流体在喷嘴入口压力约为6.99 bar，随着喷嘴的收敛，压力减小；在喷嘴出口，压力达到最小值，远低于二次流进口的1.65 bar，且压力出现不规则变化。混合室下游的压力逐渐增大，在喷射器出口处压力在2bar 左右，满足电堆的需求。干气模型计算的压力分布变化大于组分输运-相变模型，且波峰波谷值的出现将对较早。由此表明凝结现象产生的液滴促进了气液两相的换热，减缓和推迟了压力振荡，减小压力波动时的误差。

图2 基于组分输运-相变模型和干蒸汽模型的喷射器内流体压力云图

图3 为基于组分输运-相变模型和干蒸汽模型计算的喷射器内部速度分布图。喷射器内速度分布变化方向与压力分布变化方向几乎相反，这是由于压力势能与动能相互转换所致。两种模型的激波形态相似，但局部速度存在一定差异。对于第一峰值，相变模型的马赫数在2.00 左右，而干蒸汽模型马赫数为1.98；第一谷值相变模型马赫数约为1.60，干蒸汽模型马赫数约为1.49；两模型在等面积段和扩散段的最大马赫数差约为1.71；这意味着低估了膨胀程度可能会导致基于干蒸汽假设的引射比被低估。

图3 基于组分输运-相变模型和干蒸汽模型的喷射器内流体速度云图

图4(a)和图4(b)显示了不同湿度和压力下引射比波动情况。在一定条件下，由组分输运-相变模型计算的引射比比由干蒸汽模型计算的值高13.2%，误差低约5.6%。这表明，组分输运-相变模型可以更准确的预测不同状态方程和流体性质(密度、比热、粘度等)，比干蒸汽模型更适合分析喷射器内部流动结构和性能。

图4

4 结论

喷射器对于PEMFC 系统来说是至关重要的，它可以将未消耗的氢气再循环。本文针对喷射器二次流含有多种气体且内部流体结构复杂，建立了组分输运-相变模型，并利用流行的商业CFD 软件包Fluent进行仿真。通过与干蒸汽模型对比发现，考虑相变和组分输运后，考虑与凝结相关的热传质，压力分布最大差异约14.3%，等面积段和扩散段马赫数最大差约1.71，引射比更高。因此可以得出结论，在预测PEMFC系统喷射器的流动特性和引射性能时，必须重视组分输运、冷凝和相变现象。