不同本构模型对近接施工力学响应的影响研究
马玉岩,闫飞跃,程丽娟
(1.中国电建集团成都勘测设计研究院有限公司,四川 成都 611130;2.西南交通大学,四川 成都 610031)
0 前 言
岩土体的本构模型反映了岩土体的力学特性,包括应力、应变、强度和时间4者之间的关系。岩土体的本构模型总体可划分为弹性模型、弹塑性模型、黏-弹塑性模型以及损伤模型等几个大类。目前,已经有许多种描述岩土体力学特性的本构关系,其中工程中应用比较广泛的土体模型有:Mohr—Coulomb模型、Cysoil模型、K-G弹性模型、E-B模型、邓肯E-ν模型等弹性模型和弹塑性模型[1~4]。
近接施工在城市地铁修建中是不可避免,数值模拟是解决工程问题重要手段之一,合理地选择岩土体的本构模型是获得合理数值分析成果的前提。国内外学者依托工程实践,对本构模型在基坑工程数值模拟的影响以及基坑工程近接既有建(构)筑物的施工开展了大量的研究。秦会来等(2012)[5]对比分析修正剑桥模型和Mohr-Coulomb模型的基坑开挖二维数值模拟结果,认为Mohr-Coulomb模型不能反映加卸载模量差异和土体压硬性,故不适用于基坑开挖引起的变形模拟;蒋进等(2020)[6]对比分析修正剑桥模型、Mohr-Coulomb模型与Drucker-Prager模型的基坑开挖三维数值模拟结果,发现Mohr-Coulomb模型与Drucker-Prager模型的基坑侧壁地表边缘在开挖后出现隆起变形;马琳(2018)[7]以昆明某基坑工程近接地铁1号线施工为背景,研究了基坑开挖对车站及基坑本身的变形影响;杨俭(2018)[8]以珠海某邻近车站结构的深基坑工程为依托,研究了基坑工程施工对邻近车站结构及其周围土体的影响规律。但是在本构模型对深基坑工程近接既有地铁车站结构施工方面的力学响应影响方面研究很少。
本文以成都地区的一紧邻地铁车站的大型基坑工程为例,利用FLAC3D开展近接施工力学响应的研究,通过岩土体变形、地铁结构变形及受力特征的对比分析,研究不同本构模型的异同和适用性,为类似近接工程提供参考。
1 工程概况
成都市锦城广场站是成都轨道交通18、16、29号线三线换乘站,三站两两相交,呈三角形布置。18号线为南北走向,锦城广场站为地下四层岛式车站,场坪标高491.5m,底板埋深32.4~34.2m,外包总长为367.458m,标准段宽21.7m。16号线位于18号线东侧,为西南—东北走向,16号线锦城广场站为地下三层岛式车站,场坪标高491.5m,底板埋深24.3~24.5m,总长为306m,标准段宽20.7m,基坑支护采用直径1.2m,间距1.8m的排桩结构,插入中等风化泥岩内4m。29号线位于18号线东侧、16号线北侧,为西北—东南走向,站台层位于地下五层,底板埋深约41m。三条地铁线车站围成的三角形区域为地铁换乘大厅,底板埋深约为24~24.5m。锦城广场站及地铁大厅均采用框架结构体系,其中18号线主体结构(含与16号线、29号线换乘节点)已施工完成,本项目为实施紧邻18号线主体结构的三角换乘区及16号线。
本项目的平面与剖面位置关系分布如图1~2所示。
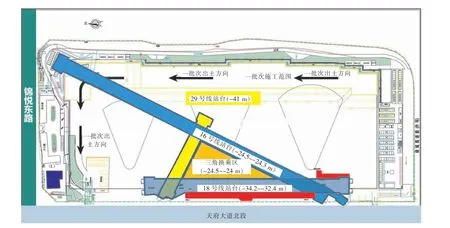
图1 项目平面示意

图2 项目剖面示意
2 本构模型介绍
2.1 Mohr-Coulomb模型
Mohr-Coulomb模型是工程中运用最广泛的一种本构模型,对于剪切破坏包络线上的应力点服从非关联流动法则,而拉伸破坏为关联流动法则,模型破坏包络线包含剪切屈服函数及拉伸屈服函数,模型破坏准则见图3。
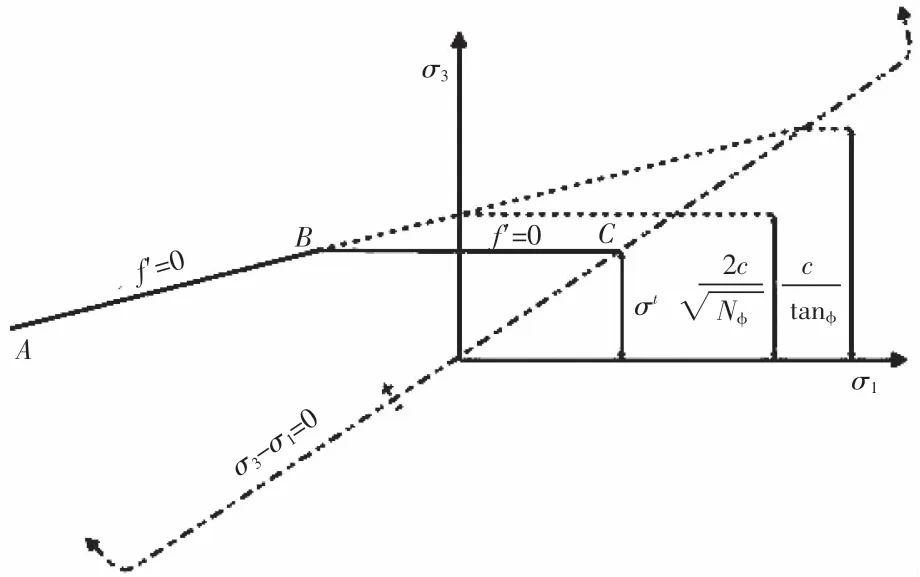
图3 摩尔库伦破坏准则
对于剪切破坏准则fs=0,通过A点到B点的直线方程见式(1):

对于拉伸破坏准ft=0,通过B点到C点的直线方程见式(2):

式中:Φ为摩擦角,c为黏结力,σt为拉伸强度,NΦ=
材料的拉伸强度不能超过fs=0与σ1=σ3相交点的σ3值。

2.2 Cysoil模型
岩土体的塑性变形在微观上表现为颗粒重分布及颗粒破裂。针对土的力学行为,双屈服面模型考虑了剪切和体积硬化/软化,此模型最大的特点是可以通过自定义硬化/软化曲线,通过在平均应力轴上戴“帽盖”的方法来移动封闭屈服面来考虑主应力增加引起的塑性变形。在双屈服面模型中,在应力空间中这个“帽盖”的形状为平面,其法向为平均应力主轴方向。但是通过单轴压缩试验已经证实,这个“帽盖”的形状对侧压力系数的影响很大。Cysoil模型修正了双屈服面模型,将“帽盖”的形状改进为椭圆。模型服从体积准则和流动准则:
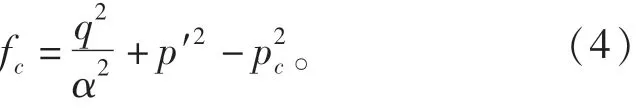
式中:p′为平均有效应力,pc为帽子压力,α为无量纲常数,用于定义椭圆帽子屈服面。其p′与体积应变e关系曲线如图4所示。图4中Ke为弹性模量;H为硬化模量;R=Ke/H为常数。

图4 等向压缩试验p′与e关系曲线
3 计算模型与参数
3.1 计算模型
开挖三角换乘区及新建16号线近接既有18号线的三维计算模型如图5所示,模型边界范围取3~5倍基坑开挖深度,影响深度取开挖深度的2~4倍,计算模型侧向加水平约束,底部加固定约束,顶面为自由面。模型中岩土体、三角换乘区、地铁车站及附属结构为三维实体单元,围护桩和抗拔桩采用桩结构单元,预应力锚索采用锚索单元。其中结构单元采用弹性模型,而对岩土体分别采用Mohr-Coulomb理想弹塑性模型和Cysoil模型进行研究。

图5 三维计算模型
3.2 计算参数
工程场地从上到下分布的地层依次是:①杂填土;②黏土;③粉土;④卵石土;⑤中风化泥岩。各地层Mohr-Coulomb模型的物理力学参数依据勘察报告中给出的地层物理力学参数建议值选取如表1,通过数值、室内三轴试验及现场压剪试验确定Cysoil模型的物理力学参数如表2所示,结构的物理力学参数按规范取值。

表1 Mohr-Coulomb模型材料参数

表2 Cysoil模型材料参数
4 近接施工力学响应影响分析
4.1 对岩土体及结构变形特征的影响分析
4.1.1 开挖至地下两层底板标高
对既有车站结构两侧的土体同步进行分层开挖,Mohr-Coulomb模型(以下简称M-C模型)与Cysoil模型(以下简称C-Y模型)下开挖完成后的竖向位移和水平位移云图如图6~7所示。
由图6竖向位移云图可以看出,基坑的开挖引起了既有车站结构两侧和底部土体不同程度的卸荷回弹,由于东侧基坑的开挖面积较大,使得东侧基坑的回弹大于西侧基坑;在西侧基坑地表变形方面,M-C模型为隆起,C-Y模型为沉降,且M-C模型的影响范围较C-Y模型大。由图7水平位移云图可以看出,西侧基坑侧壁变形方面,C-Y模型的水平位移比M-C模型大。

图6 开挖至地下两层底板标高竖向位移云图
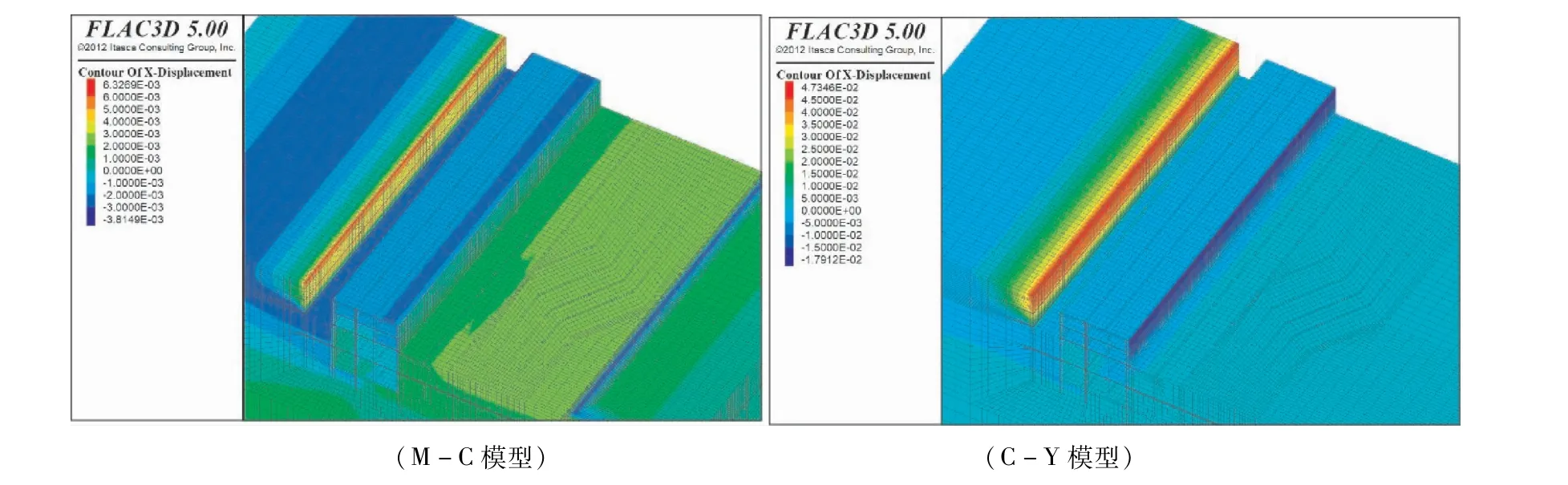
图7 开挖至地下两层底板标高水平位移云图
4.1 .2 施工逆筑部分底板和上部结构
施工完逆筑部分底板和上部结构模型的竖向位移和水平位移云图,如图8所示,由竖向位移可以看出,被开挖的部分,坑底出现了卸荷回弹,导致逆筑的结构和既有车站结构出现了向上的位移,随着与开挖土体距离的增大,既有车站结构底部岩土体的回弹逐渐减小,既有车站结构的变形也在逐渐减小,之后上部结构的施作对基坑底部土体进行了再压缩,M-C模型与C-Y模型下基坑底部土体再压缩的变形规律及带来的结构变形规律相似。

图8 施工逆筑部分底板和上部结构竖向位移云图
4.2 对既有车站结构的变形影响分析
为了能更直观地研究M-C模型与C-Y模型下近接施工对既有车站结构的变形影响规律,对计算结果进行了整理,研究了既有车站结构竖向(Z方向)的变形规律,位置如图9所示。由于有的施工步相比前一施工步的计算结果变化不大,折线图仅对比了变化大的四个关键施工步:step1为开挖至地下三层底板标高;step2为施工完新建16号线结构、逆筑部分顶板和桩柱;step3为开挖完预留的8m宽土体;step4为施工完逆筑部分的底板和上部结构。
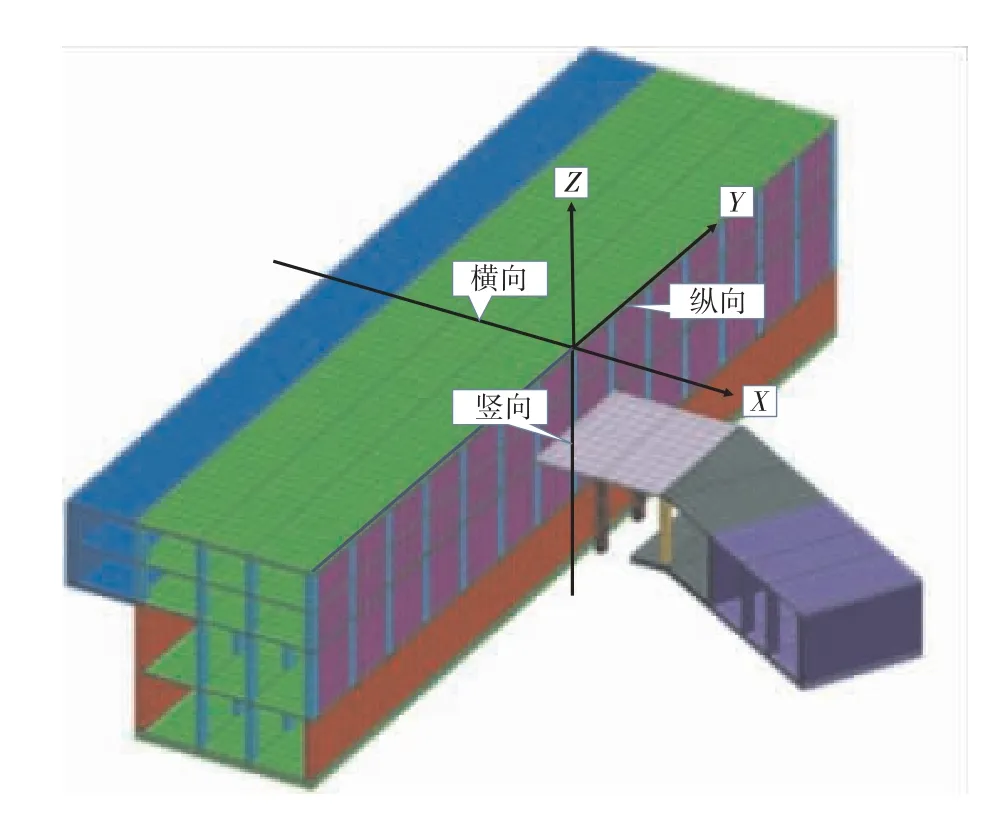
图9 变形研究位置示意
不同本构关系模型下既有车站结构沿Z轴规律如图10所示,M-C模型下施工完step1后,既有车站结构东侧墙柱的水平位移表现为下小上大,地下四层底板(Z=86.4m)位置的水平位移接近于零,地下三层中板(Z=95.36m)位置的水平位移为-0.1mm,地下二层中板(Z=105.01m)位置的水平位移为-0.3mm,地下一层中板(Z=110.56m)位置的水平位移为-0.2mm,地下一层顶板(Z=115.86m)位置的水平位移为-0.25mm。施工完step2后,既有车站结构的水平变形变化不大。施工完step3后,地下四层底板(Z=86.4m)位置的水平位移变化不大;地下三层中板(Z=95.36m)位置的水平位移为-0.5mm,这是因为地下四层底板受到开挖土体卸荷回弹和地下三层中板水平支撑的影响,所以该层侧壁出现了先向左变形至-0.6mm,又向右变形;地下二层中板(Z=105.01m)位置的水平位移为0.2mm,这是因为地下二层中板从原来受到东西侧土体侧压力的平衡状态变为东侧土体开挖后由逆筑板提供水平支撑的状态;地下一层中板(Z=110.56m)位置的水平位移变化不大;地下一层顶板(Z=115.86m)位置的水平位移变化不大。施工完step4后,既有车站结构的水平变形变化不大。C-Y模型和M-C模型的既有车站结构沿Z轴变形规律相同,只是在数值上有所差异,且差别不大。
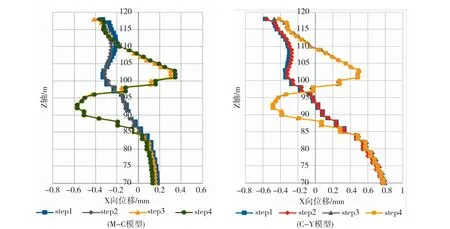
图10 既有车站结构沿Z轴横向变形规律
4.3 对既有车站结构的应力影响分析
4.3.1 开挖至地下三层底板标高
基坑开挖至地下三层底板标高,并预留了8m宽的土体在既有车站结构的东侧。开挖完成后MC模型与C-Y模型下的最大主应力值的最大正值分别为1.33MPa、1.49MPa,最小主应力值的最大负值分别为5.29MPa、6.23MPa,其中最大主应力为拉力,出现在梁板和柱的连接处,最小主应力为压力,从地下一层顶板到地下四层底板,结构板受到的压应力逐渐增大,M-C模型与C-Y模型下的压应力水平相当。
4.3.2 施工逆筑底板和上部结构
逆筑底板和上部结构施工完成后,M-C模型与C-Y模型下的最大主应力值的最大正值分别为1.29MPa和1.50MPa,M-C模型与C-Y模型下的最小主应力值的最大负值分别为-5.35MPa、-6.35MPa,由于施作结构的自重作用对结构模型受力影响不大。
5 结 论
(1)与Mohr-Coulomb模型相比,Cysoil模型所需的计算参数比较复杂,需要通过数值分析及现场试验才能比较准确地确定相关参数。
(2)当选用Mohr-Coulomb模型时,由于该模型卸荷回弹时回弹模量和加载时的弹性模量相同,导致不真实的回弹变形,数值计算结果误差较大。特别是进行基坑计算时回弹变形较大,采用Mohr-Coulomb模型基坑底部隆起很大,造成基坑周边地表出现隆起,计算结果失真;而Cysoil模型可以有效解决基坑周边地表的异常隆起现象,相对更加真实 地反映基坑开挖导致的地层变形规律。
(3)通过Mohr-Coulomb模型和Cysoil模型在近接施工中对既有车站结构的变形及受力特征影响规律的研究,可以看出两种模型下既有结构力学响应规律相同,只是在数值上有所差异,且差别不大,在具体工程设计中,若仅分析近接施工对既有构筑物的影响,仍可采用M-C模型。

