张力腿平台涡激运动模型试验与数值分析
呼文佳,王世圣,赵晶瑞
(中海油研究总院有限责任公司,北京 100028)
张力腿平台在位期间,不可避免要承受海流载荷作用。流通过平台立柱后将发生不连续的旋涡脱落,当旋涡的脱落频率接近平台的自振频率时,会发生共振现象,诱发平台产生较大动力响应,对平台结构,尤其是张力腿和立管造成严重的疲劳损伤。浮体的涡激运动与张力腿和立管涡激振动互相影响,平台的动力响应是两者的叠加。针对涡激运动的研究方法主要有数值模拟和模型试验。数值模拟基于黏性流体力学理论,采用数值计算的方法计算浮式平台的涡激运动响应[1],Chen和Chen[2]、 GU等[3]和LIU等[4]采用数值模拟方法研究深吃水半潜式平台的涡激运动响应,确定了锁频条件。赵伟文和万德成[5]采用自主开发计算流体动力学(CFD)求解器模拟了深吃水对柱式半潜平台涡激运动响应,模拟结果表明,在折合速度5~9时发生共振,出现锁频现象。胡晓峰等[6]采用改进的延迟分离涡方法(IDDES)数值模拟深吃水半潜平台的涡激运动,研究深吃水半潜平台在0°、22.5°和45°流向角下的纵向、横向和艏摇运动响应,以及吃水和立柱倒角对半潜平台涡激运动的影响。计算结果表明横向运动出现频率锁定现象,但不同流向角下的锁定区域不同。田辰玲等[7]采用分离涡模拟方法,研究了均匀流作用下三立柱轻型半潜式生产平台涡激运动响应,研究表明折合速度在7~10之间出现锁频现象,180°流向角时响应幅值最大。数值模拟方法参数调整方便、成本低,是模型试验重要的补充手段。目前国内外开展的水池模型试验基本为拖曳水池模型试验。Maximiano等[8]采用拖曳水池试验,研究了半潜船的涡激运动,发现添加合理水平的线性阻尼可以显著降低涡激振动响应(VIM)幅值。田辰玲等[9]、Tian等[10]和李磊等[11]采用拖曳水池试验的方法开展了张力腿平台涡激运动响应研究,获得了张力腿平台在均匀流作用下涡激运动响应规律。该试验模型不包括系泊和立管系统,仅利用垂向轴承系统模拟载荷或采用截断系泊的方式计算系泊运动响应。
拖曳水池模型试验采用等效横向系泊和施加垂直压载的模拟方式,可以模拟平台的吃水和系统刚度。将该方法运用到张力腿平台涡激运动水池试验中,可以得到浮体涡激运动响应,但不能获得张力腿、立管自身的涡激振动响应。因此,关于全水深下缩尺模拟研究尚未见于国内外文献。全水深系泊张力腿平台试验模型包括浮体、张力腿和立管模型,三者构成一个完整的模型试验系统。在试验中可以通过测量测点的位移、加速度分析张力腿和立管的涡激振动响应,并结合平台浮体涡激运动测量数据分析浮体与系泊系统间的相互影响。
以传统式张力腿平台为研究对象,开展了均匀流、剖面流作用下全水深系泊张力腿平台的涡激运动数值模拟与模型试验,通过模型试验结果与数值模拟结果对比、分析,发现了在均匀流、剖面流作用下的平台涡激运动,以及张力腿和立管涡激振动响应规律。研究所获得结论对于张力腿平台工程设计有一定指导意义。
1 试验模型与数值模拟模型
1.1 全水深系泊试验模型
张力腿平台全水深系泊水池试验模型采用的缩尺比为1∶61,模型包括:张力腿平台主体、8根张力腿、4根TTR立管。模型试验水池的有效工作尺寸为456 m×5 m×12 m(长×宽×高)。1∶61缩尺比可以满足相似要求和试验场地的水深要求,能够准确模拟张力腿平台在位工况下的吃水条件,进行全水深模拟。张力腿平台主尺度参数与模型参数如表1所示。张力腿平台系统水池试验装置示意、试验布置与坐标系和试验装置如图1~3所示。
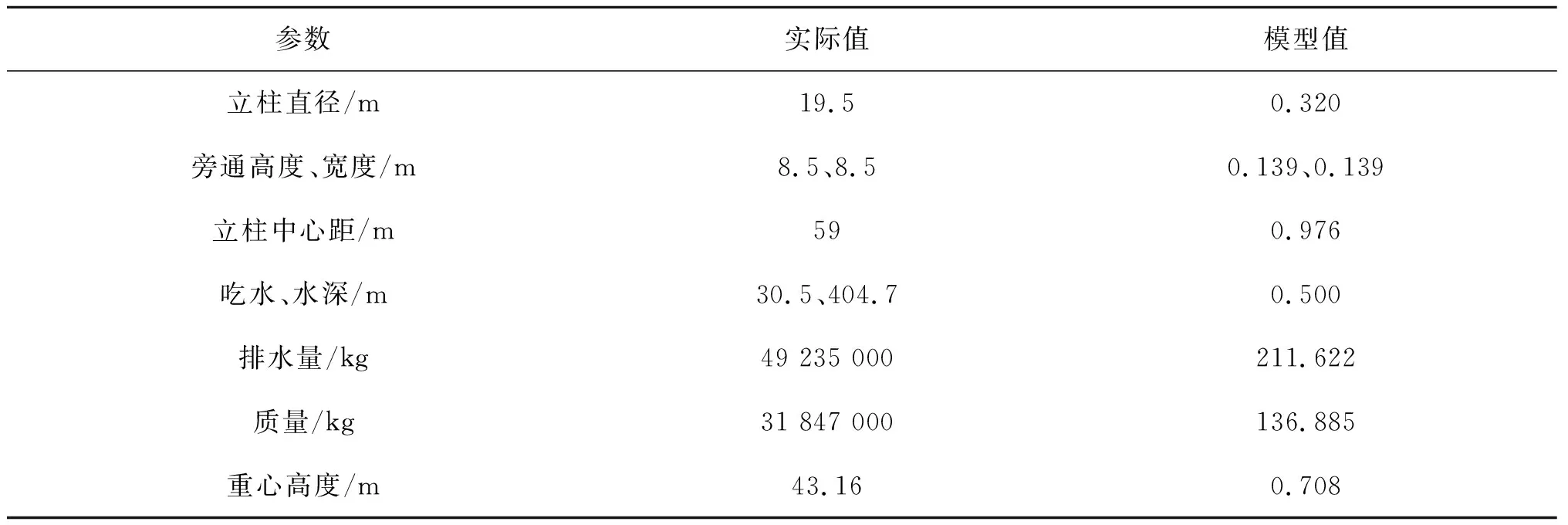
表1 TLP主尺度参数Tab. 1 TLP main scale parameters

图1 全水深系泊试验示意Fig. 1 Full water depth mooring test diagram

图2 试验布置与坐标系Fig. 2 Test layout and coordinate system

图3 张力腿平台涡激运动试验装置Fig. 3 Test device for tension leg platform vortex-induced motion
1.2 数值模拟模型
数值模拟采用涡激振动精细虚拟试验系统 viv-FOAM-SJTU,该系统以计算流体力学理论为基础,采用分离涡模拟方法处理高雷诺数下三维流动分离,结合物体六自由度运动理论和动网格技术求解平台涡激运动。在结构场计算部分,将管柱视为欧拉—伯努利梁模型进行处理,通过求解结构控制方程获取各结构节点的振动位移。基于CFD数值模拟所建立的数值模型与模型试验比例为1∶1,参考模型试验时试验水池的条件,建立一个尺寸为8 m×5 m×8 m(长×宽×高)的长方体计算域,或称为数值水池。数值水池深度6.63 m,其中数值水池的宽和水深与试验条件一致。
在进行数值模拟时首先对所用的网格和时间步长进行收敛性分析。收敛性分析及精度验证模拟采用三种不同数量的网格(155万、377万、587万)及三种不同的时间步长(T/100、T/200、T/300)。收敛性分析及精度验证结果如表2、3所示。

表2 网格收敛性分析结果Tab. 2 Grid convergence analysis results

表3 时间步长收敛性分析结果Tab. 3 Convergence analysis results of time step
最后通过比较分析并综合所有因素选取了377万网格、T/200时间步长进行模拟,模拟计算精度满足要求。
1.3 试验与模拟工况
模型试验综合考虑水槽造流对流速精度控制的能力,折合速度Ur范围选取为4~12,取值间隔为1.5,流速覆盖目标海域一年一遇(表面流速1.5 m/s)、十年一遇(表面流速1.7 m/s)、百年一遇海况(表面流速2.3 m/s)。
2 均匀流、剖面流作用下涡激运动响应
采用数值模拟与水池模型试验结合的方法研究了在不同来流方向、折合速度的流作用下张力腿平台涡激运动响应特性。模型试验中选取来流方向为0°、22.5°、45°,折合速度Ur=4.5~11.5。
课堂教学中教师可以利用平台针对某个知识点或者一节课的所有知识点,做一次课堂检测,由于平台可以同步看到学生的答题情况,汇总统计答题的结果,这样教师就能够根据随堂练习的反馈结果及时把握学生的掌握情况,及时对学生进行分层式的个性化指导,也便于后面教学内容的调整。
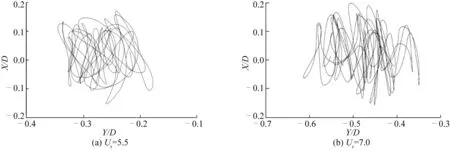
图4给出在0°来流角均匀流作用下平台横向运动标称响应幅值及横向运动最大响应幅值随折合速度的变化曲线。响应幅值曲线从Ur=4时开始统计绘制,数值存在一个不断增大的过程,在Ur=7时张力腿平台进入锁定区,最大响应幅值达到最大值0.32D。当Ur>8.5时张力腿平台脱离锁定区,响应幅值开始逐渐减小。张力腿平台涡激运动响应随折合速度变化而变化,在折合速度5.5 图4 0°来流均匀流作用下横向运动标称响应幅值和最大响应幅值变化曲线Fig. 4 Nominal response amplitude and maximum response amplitude of lateral motion at different reduced velocities under the action of uniform flow of 0° incoming flow 涡激运动与普通的机械共振所不同的是,共振不只是在一个很窄的频带内发生,锁定效应扩大了产生共振的折合速度范围,锁定现象可在相当一部分折合速度范围内持续,导致长时间持续的运动。这也是涡激运动对平台结构、立管和系泊系统安全性都会产生重要影响的原因。 根据数值模拟和模型试验结果,对不同折合速度、不同来流角度下张力腿平台的横荡、纵荡响应进行比较,张力腿平台处于三种来流角时,均在Ur=7时达到该来流角下的横荡响应最大值,说明平台不论位于何种来流角度下,均在该来流速度下发生剧烈的涡激运动,之后随着来流速度的上升,响应幅值开始下降,平台的横荡运动逐渐平缓,涡激运动响应规律表现一致。对不同来流角进行分析,来流角度对横荡响应的影响很大,当来流角为0°时横荡涡激运动响应最大,最大响应幅值为0.32D;当22.5°来流角时横荡涡激运动响应最大幅值为0.27D;当来流角为45°时平台横荡涡激运动响应最小,最大响应幅值为0.19D。 剖面流为垂向流速分布不同的流。剖面流是依靠设计的一套可局部增大流速的涡激运动试验装置来实现,如图5、6所示。流速增大装置通过支撑装置固定在水池边壁上,来流在过渡区和加速区产生加速,经由张力腿平台所在稳定区位置时,来流速度可提升20%以上。 图5 流速增大装置Fig. 5 Flow increasing device 图6 流速装置效果Fig. 6 Effect of flow increasing device 在45°来流角剖面流作用下平台横向运动最大响应幅值及流速装置位于纵深不同位置时的横荡最大响应幅值与均匀流工况的对比曲线,如图7、8所示。由图8可知,流速装置置于水下50 cm处时,平台发生了更为剧烈的横荡响应和艏摇响应;当流速装置置于水池表面时,因水池造流的模式和流速装置的影响,流场表面产生了一定的波浪,对横荡和艏摇响应产生了影响,因此位移响应呈现了不同的趋势。 图7 剖面流作用下横向运动最大响应幅值Fig. 7 Maximum response amplitude of lateral motion under the action of profile flow 图8 剖面流影响下横荡最大响应幅值对比Fig. 8 Comparison of the maximum response amplitude of sway under the influence of profile flow 根据图7的数值模拟和模型试验结果表明,在45°来流角剖面流作用下张力腿平台涡激运动响应随折合速度变化而变化,在折合速度5.5 图9 45°来流角均匀流不同折合速度下平台在XY平面内的运动轨迹Fig. 9 The trajectory of the platform in the XY plane under different reduced velocities of the 45°incoming angle uniform flow 图10 45°来流角剖面流不同折合速度下平台在XY平面内的运动轨迹Fig. 10 The trajectory of the platform in the XY plane under different reduced velocities of the 45°incoming angle profile flow 根据图9,45°来流角均匀流作用下,由于平台自身结构呈对称形式,此时横流向响应远大于顺流向响应,因此平台轨迹呈现对称结构“8”字形,平台运动轨迹的丰满和扁平由顺流响应和横流响应的大小决定,当能量峰值集中时,平台的运动轨迹显得更为规律,大量“8”字形在一个轨迹上运动。 根据图10,45°来流角剖面流作用下在折合速度5.5 全水深系泊TLP涡激运动数值模拟与模型试验研究考虑了浮体涡激运动与张力腿和立管的涡激振动的相互影响。在来流作用下浮体的涡激运动与张力腿和立管涡激振动的耦合作用使得张力腿和立管呈现复杂的非线性振动特性。在0°来流角度,均匀流作用下1号张力腿和1号立管所受拉力变化如图11所示。 图11 0°来流角均匀流下1号#张力腿、1号立管拉力时历响应曲线Fig. 11 No. 1 tension leg and No. 1 riser tension time history response curve under the action of uniform flow of 0° incoming flow 由图11可知,随着流的经过,平台在流的作用下偏移到一个新平衡位置,由于张力腿和立管提供拖曳力的作用,平台在流向平衡位置处做往复运动。张力腿、立管所受拉力幅值随折合速度变化曲线如图12所示,张力腿拉力幅值变化与艏摇的对比关系如图13所示。 图12 张力腿、立管所受拉力幅值变化曲线Fig. 12 Tension leg and riser′s tension amplitude change curve 图13 张力腿拉力与艏摇对比Fig. 13 Comparison of tension leg tension and yaw 由图12可知,在顺流向拖曳力作用下,平台发生大幅度纵向位移,系统整体极大程度偏离初始位置,导致张力腿、立管拉力数值随折合速度增大,对比图4(b),张力腿、立管拉力并没有在横向涡激运动幅值最大值附近出现最大拉力。图13所示,艏摇运动与张力腿拉力变化存在相同的趋势,艏摇运动与系泊系统的关系极为紧密。在中低折合速度条件下,平台横荡运动的变化规律与张力腿拉力的变化一致,均随水流速度的增加而增加,且张力腿、立管拉力并没有在锁定区间即Ur=7附近出现极值,反而随着流速的增加而不断增大,由此可见锁定现象的出现主要源于横流向的升力作用,并非由张力腿、立管提供的拉力导致的,但系泊系统所提供的回复力能有效地控制涡激运动幅值。 当流流经张力腿和立管时会在管柱的两侧产生交替的泄涡,导致管柱受到横流向和顺流向的脉动流体力。研究主要关注了横流向的涡激振动和模态。在均匀流作用下,来流角和折合速度对张力腿、立管振动模态有明显的影响。图14为折合速度 7.0,不同流向角均匀流作用下 4号张力腿振动模态,图15为折合速度8.5,不同流向角均匀流作用下 4号张力腿振动模态。 图14 折合速度 7.0,不同流向角均匀流作用下 4号张力腿振动模态Fig. 14 Vibration mode of No. 4 tension leg under the action of uniform flow with different flow direction angles at a reduced velocity of 7.0 图15 折合速度 8.5,不同流向角均匀流作用下 4号张力腿振动模态Fig. 15 Vibration mode of No. 4 tension leg under the action of uniform flow with different flow direction angles at a reduced velocity of 8.5 根据图14、15所示,当外界来流速度为Ur=7.0时,4号张力腿在所有来流角度下涡激振动的响应包络图均为半个上下对称的正弦波,与张力腿的第一阶模态相类似。这说明位于此种流速下,张力腿的第一阶模态主导涡激振动响应。当外界来流速度为Ur=8.5时,4号张力腿位于0°来流条件下,仍呈现一阶模态;在22.5°和45°来流条件下,涡激振动响应状态的包络图表现为由半个正弦波逐渐向一个完整的上下对称正弦波过渡的状态,向第二阶模态靠拢,此时第二阶模态主导涡激振动响应。 张力腿的响应在不同来流角度下导致差异的原因是水流经由张力腿平台模型上游立柱和张力腿后,发生了旋涡脱落等复杂的流场现象。不同的来流角时,水流经由上游立柱、张力腿后,脱落的旋涡直接影响到位于其正后方的下游结构,来流角不同,产生遮蔽效应有差别,流速变化幅度不同,因此下游张力腿出现一阶、二阶模态交替主导的状态。另外,张力腿涡激振动响应模态数除了与水流速度相关,还与顶部预张力相关。0°来流角度张力腿平台主体发生的横荡运动响应幅值大于22.5°和45°来流角工况,因此TLP主体与张力腿间的耦合作用更加强烈,0°来流情况下张力腿顶部预张力总是大于其他两种工况。因此,随着顶部预张力的增大,张力腿结构振幅变小,模态相应降低,因此0°来流角下Ur=7.0、8.5时,张力腿始终处于一阶模态主导状态。 根据水池试验结果,通过对比张力腿在均匀流和剖面流作用下的位移模态响应,发现张力腿受剖面流影响较小,仅在剖面流装置对应的垂向位置出现了位移的小幅度上升和模态的微弱变化。 1) 张力腿平台在均匀流、剖面流作用下涡激运动都表现为浮体位于水平面内的幅值较大的往复运动,横荡运动在折合速度5.5 2) 张力腿平台在流的作用下发生偏移,其涡激运动是在平衡位置上的往复运动。在中低折合速度条件下,张力腿、立管拉力没有在锁定区间即Ur=7附近出现极值,而是均随流速增加而增加,系泊系统能够提供更大的回复力,有效地控制涡激运动幅值。 3) 均匀流作用下,来流角和流速对张力腿或立管涡激振动模态影响显著,由于遮蔽效应的差别,以及流速引起顶张力不同,而呈现一阶、二阶模态交替主导的状态。剖面流与均匀流造相比,水面制造剖面流时产生一定波浪,对涡激运动起到了减小作用。剖面流对张力腿、立管振动特性的影响主要表现在位移的小幅度上升和模态的微弱变化。





3 立管、张力腿响应特性





4 结 语

