纵向风和阻塞比对隧道双火源温度分布的影响*

马 鲜，万华仙,2，张玉春

(1.西南交通大学 地球科学与环境工程学院，四川 成都 611756；2.中国科学技术大学 火灾科学国家重点实验室，安徽 合肥 230026)

0 引言

随着世界公路隧道数量快速增长，隧道内发生火灾的频率也在逐渐增加。由于隧道呈狭长形受限空间，受通风条件限制，火灾产生的高温有毒烟气在隧道内聚集，易造成人员伤亡和隧道损毁[1-2]。当隧道发生火灾时，一方面，隧道内自然通风和机械通风形成的纵向风流会影响火羽流行为；另一方面，火灾易造成车辆堵塞，车辆自身作为障碍物会阻碍空气流入，形成风阻，影响火行为并对人员疏散逃生造成影响[3]。因此，开展城市公路隧道纵向通风和障碍物共同影响下的烟气行为研究具有重要意义。

温度是隧道火灾研究重要参数之一，隧道顶棚下方气体温度研究结果可为火灾自动报警系统、灭火系统等设计提供参考。以往隧道火灾研究主要集中在单个火源燃烧情况下，研究火源功率、隧道纵向风速以及障碍物等对隧道顶棚温度的影响。其中，Kurioka等[4]研究隧道纵向风速对近火源温度场的影响，并建立隧道顶棚下方烟气最高温度的经验模型；胡隆华等[5]开展全尺寸隧道火灾实验，验证Kurioka模型准确性；赵望达等[6]开展数值模拟研究发现，Kurioka模型在无风或风速很小时其预测结果误差较大。对于单火有障碍物的场景，Kayili[7]研究阻塞比和通风对隧道火灾的影响，发现阻塞比增大会导致火灾热释放速率增大，而通风速度增加会降低隧道内温度；Tang等[8]研究障碍物与火源相邻情况下顶棚最高温度，发现随着障碍物到火源距离的增加，顶棚温度呈现先增加后减小的规律；Meng等[9]数值模拟研究发现，随着阻塞比和通风速度的增加，单火羽流倾斜角度从火源下游倾斜向火源上游倾斜转变。

上文研究均基于隧道内单火源燃烧场景。但在实际隧道火灾中，往往由于车辆碰撞引起火灾。比如，2014年山西岩后隧道火灾[10]，2辆卡车相撞导致火灾，蔓延到另外33辆汽车，事故造成40死12伤。可以看出，重大隧道火灾事故往往伴随着多个阻塞车辆同时燃烧。因此，亟需开展纵向通风和障碍物影响下隧道内多火源燃烧的烟气运动行为研究。在已有研究中，Zhang等[11]研究双火源在不同纵向风速、火源功率和间距下顶棚最高温度，发现火源间距和风速越大，对顶棚下方温度影响越小；刘琼和郑烽[12]研究隧道内双火源燃烧临界风速，发现相同火源功率下，临界风速随火源间距增加而减小。但是，关于隧道多火源研究中均没有考虑阻塞比这一重要影响因素。目前尚缺乏阻塞比对隧道内多火羽流行为影响研究。

因此，本文运用FDS(Fire Dynamics Simulator)数值模拟方法开展纵向通风速度和阻塞比对隧道内双火羽流温度分布的影响研究，并建立考虑阻塞比的隧道内双火羽流在顶棚下方最高烟气温度预测模型。研究结果可为隧道火灾防治提供基础数据和理论参考。

1 模型设置

1.1 模型介绍

本文主要采用FDS6.7.0版本进行建模，其包括直接数值模拟(DNS)和大涡模拟(LES)2种类型[13]。由于LES在处理浮力和湍流相互作用时的优势较为显著，因此在火灾场景模拟计算中应用更为广泛[14]。FDS模拟数据通过与实验数据对比，验证了其用于模拟隧道火羽流温度的可行性[15-16]。

考虑到实际城市公路隧道高宽比，本文模型隧道长120 m，宽10 m，高6 m，如图1所示。2个相同火源(长4 m，宽2 m，高1.5 m)放置于隧道纵向中心线上用于模拟2辆小型车燃烧，上游火源中心距离隧道左侧出口60 m，上、下游火源相邻边距离为3 m。每个火源的火源功率增长曲线设置为t2曲线，达到稳定燃烧的火源功率固定为5 MW。模拟火源的燃料设置为丙烷(C3H8)，燃烧参数为FDS默认值。模拟阻塞车辆障碍物长度为4 m，宽度为8 m，5个障碍物高度分别为1.125，2.25，3.375，4.5，5.625 m。阻塞比通常定义为障碍物横截面面积与隧道横截面面积之比[8]，即5个阻塞比(φ)分别为15%，30%，45%，60%，75%。如图1(b)所示，障碍物与上游火源相邻边距离为5 m。隧道右侧出口为自然通风，左侧出口设置纵向通风，共设置6个通风速度(v)，分别为0，1.2，2.4，3.6，4.8，6 m/s。本文共设置30个模拟工况，隧道壁面材料设置为混凝土，其密度为2 200 kg/m3，导热系数为1.2 W/(m·K)，比热容为0.88 kJ/(kg·K)，环境温度设置为20 ℃。

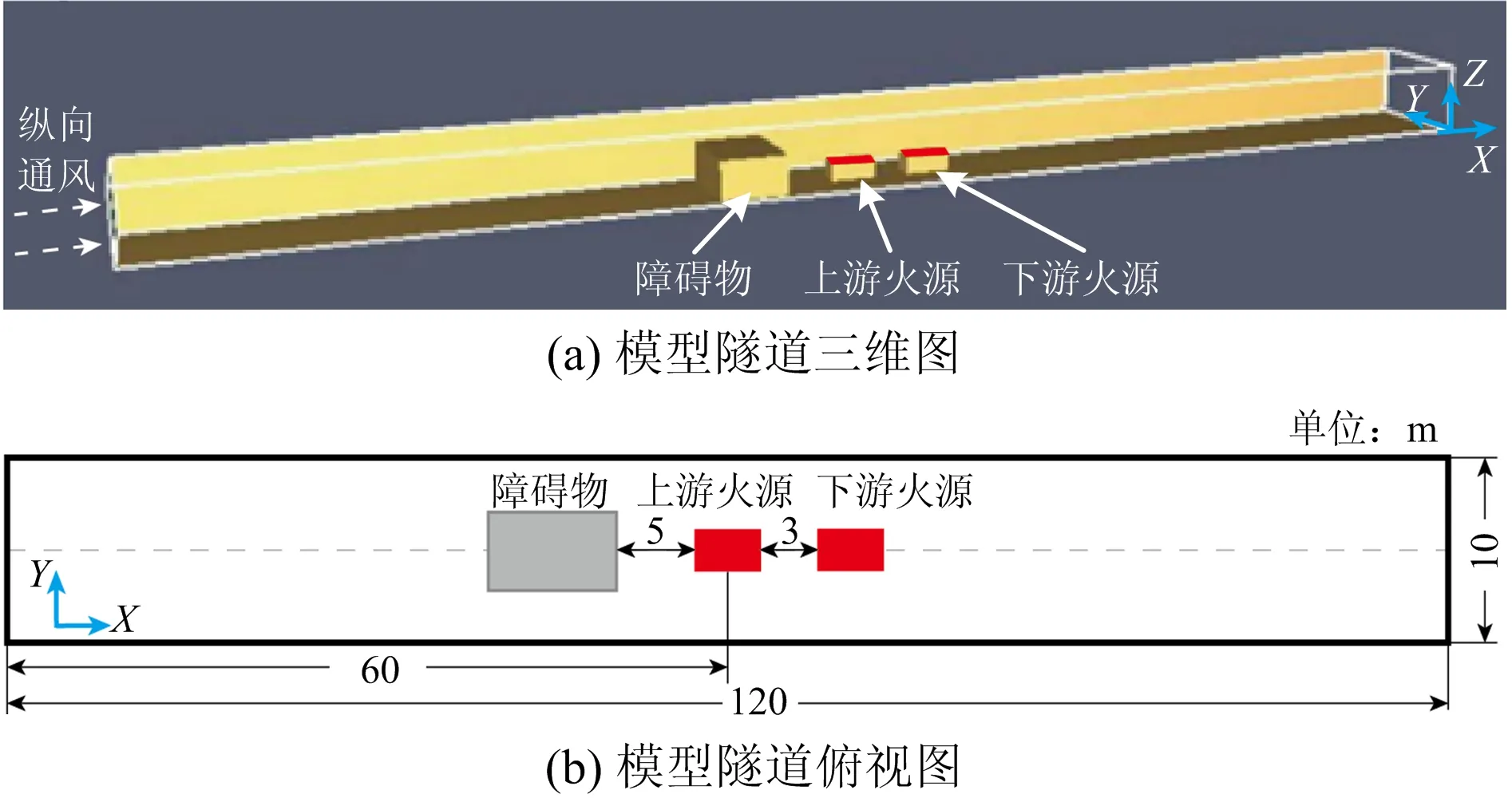
图1 阻塞场景下隧道内双火源模型示意Fig.1 Schematic diagram of double fire sources in tunnel model under blockage scene

模拟过程中，在隧道纵向中心截面Y=5.0 m、横向水平截面Z=2.0 m和Z=5.75 m分别设置温度、速度和一氧化碳(CO)体积分数切片。模拟时长设定为80 s，模拟结果表明20 s之后火源功率达到设定值，因此下文时长参数取值为60～80 s平均值。

1.2 网格选取

FDS模拟中，网格大小是影响模拟结果准确性的重要因素。FDS手册[14]中推荐了1种网格划分方法，其计算如式(1)所示：

(1)

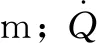
对于火源功率为5 MW的火灾，根据式(1)计算的网格尺寸在0.11～0.5 m。由此选取5种不同的网格尺寸0.1，0.125，0.167，0.25，0.5 m进行比较。图2所示为典型工况在不同网格尺寸下火源下游4 m的竖向温度分布。

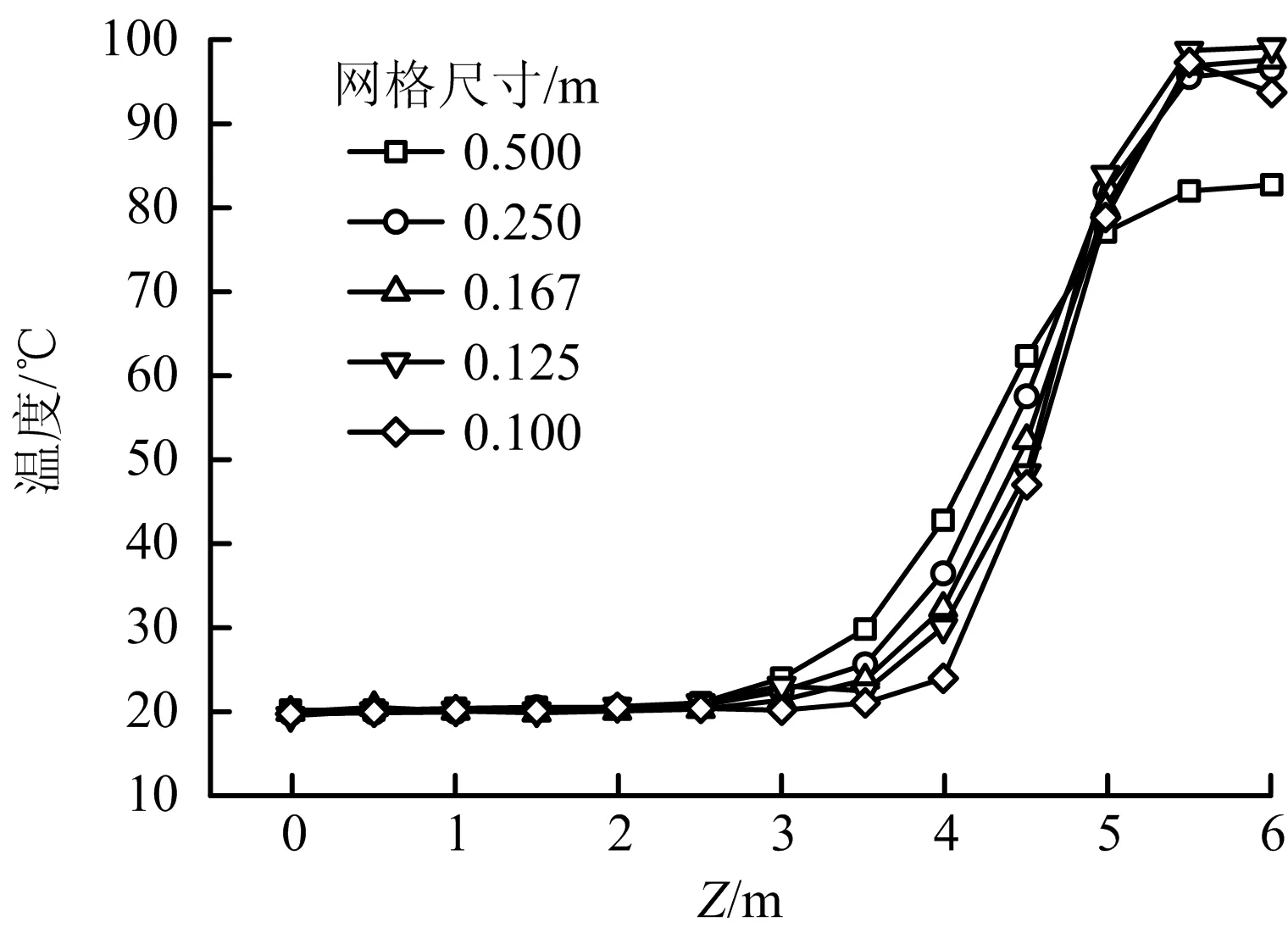
图2 不同网格尺寸下火源下游4 m处的竖向温度分布Fig.2 Vertical temperature distribution at 4 m downstream of fire source under different grid sizes

由图2可以看出，随着网格尺寸的减小，温度分布曲线趋于一致，从模拟顶棚烟气温度准确性角度看，除0.5 m网格以外，其他4种网格模拟的竖向温度值在近顶棚区域内(Z=5～6 m)相近，这意味着当网格尺寸小于0.25 m时，更小的网格尺寸只会导致更多的计算时间，而计算精度不再显著提高。因此，为保证计算精度，缩短模拟计算时间，选取网格尺寸为0.25 m。考虑到火源附近流场复杂，对该区域网格进行加密。因此在模拟中，火源近区(X=42～74 m，Y=0～10 m，Z=0～6 m)的网格尺寸确定为0.125 m×0.125 m×0.125 m(长×宽×高)，两侧火源远区的网格尺寸确定为0.25 m×0.25 m×0.25 m(长×宽×高)。

2 结果与讨论

2.1 阻塞比对纵向温度分布的影响

图3所示为通风速度v=0 m/s时不同阻塞比下，纵向中心截面在火源近区X=42～74 m的温度分布。可以看出，v=0 m/s时，双火源火焰轮廓类似，近似于对称燃烧，且不同阻塞比(φ)下均发生了明显的烟气逆流。当φ=15%，45%时，阻塞比影响较小，上、下游烟气层厚度相当；当φ=75%时，由于障碍物高度较大，阻碍烟气向上游蔓延，更多烟气流向火源下游，导致下游烟气层厚度增加。

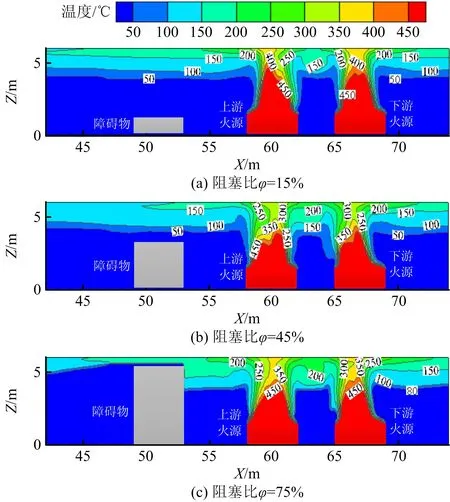
图3 v=0 m/s时不同阻塞比下纵向中心截面温度分布Fig.3 Temperature distribution of longitudinal center section under different blockage ratios at v=0 m/s

图4所示为通风速度v=0 m/s时顶棚下方0.25 m处纵向中心线上温度分布。可以看出，由于双火源的存在，出现了2个基本相同的峰值温度，且阻塞比对峰值温度影响较小；上游火源温度衰减速率大于下游火源，这可能是由于通风的冷却作用导致的；无风条件下的温度变化规律是双火源特有的，顶棚下方火源之间的区域羽流流动方向相反且竞争卷吸空气，导致该区域内温度较高，这与无风时隧道内单火源燃烧存在障碍物时只产生1个温度峰值，且在火源两侧温度逐渐下降的规律不同。

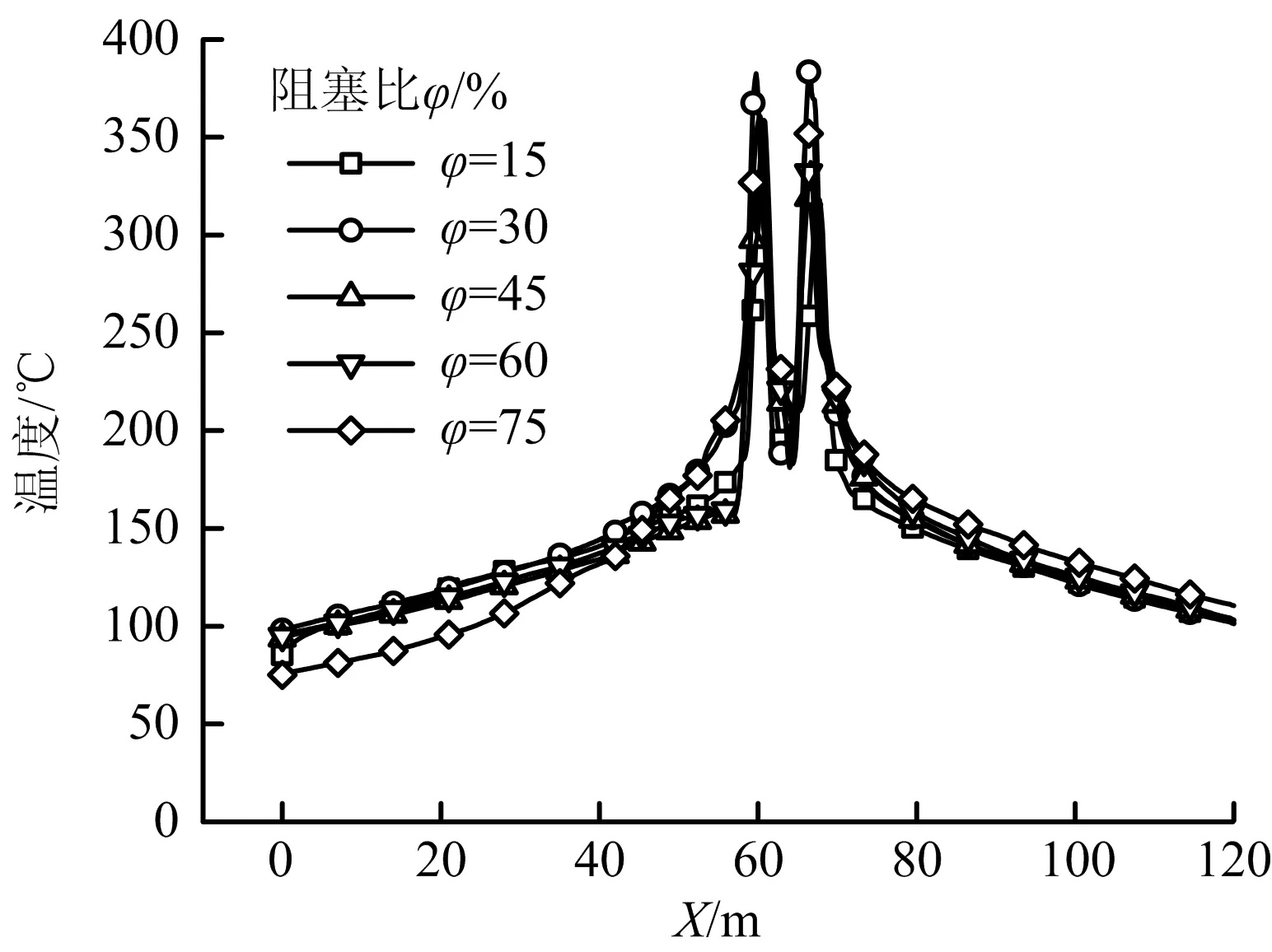
图4 v=0 m/s时不同阻塞比下顶棚下方0.25 m处纵向中心线温度分布Fig.4 Temperature distribution of longitudinal centerline at 0.25 m below ceiling under different blockage ratios at v=0 m/s

如图5所示为通风速度v=3.6 m/s时不同阻塞比下纵向中心截面温度分布。可以看出，在较大风速较小阻塞比(φ=15%)下双火焰均明显向下游倾斜，没有烟气逆流。这是由于较小阻塞比条件下，较大纵向通风对火源燃烧起主要作用。随着阻塞比增大，如图5(b)～图5(c)，障碍物对双火羽流形态影响较大，此时下游火源继续向下游倾斜，而上游火源转变为向上游的障碍物倾斜。这是由于上游火源对下游火源的遮挡作用，障碍物对下游火源影响相对较小，当风流越过障碍物表面，在障碍物与上游火源之间形成附壁效应，导致上游火羽流向障碍物方向倾斜，且风速越大，附壁效应越明显。

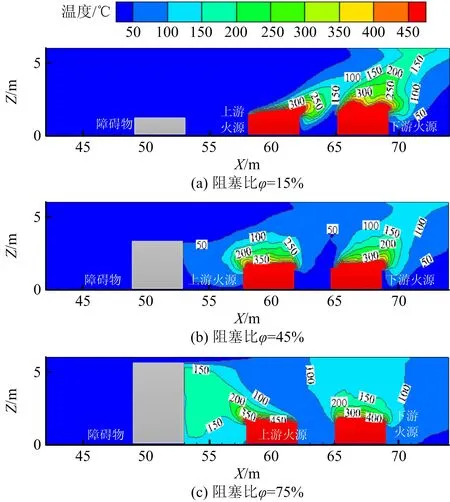
图5 v=3.6 m/s时不同阻塞比下纵向中心截面温度分布Fig.5 Temperature distribution of longitudinal center section under different blockage ratios at v=3.6 m/s

如图6所示为通风速度v=3.6 m/s时顶棚下方0.25 m处纵向中心线温度分布。可以看出，该风速下纵向温度只有1个峰值，出现在下游火源的下游，且相比于v=0 m/s时，温度峰值大幅度降低。此外，随着阻塞比从15%增大到75%，峰值温度呈现下降趋势，这是因为随着阻塞比增大附壁效应增强，导致上游火源更多向障碍物倾斜，更少热量流向下游，顶棚峰值温度降低。

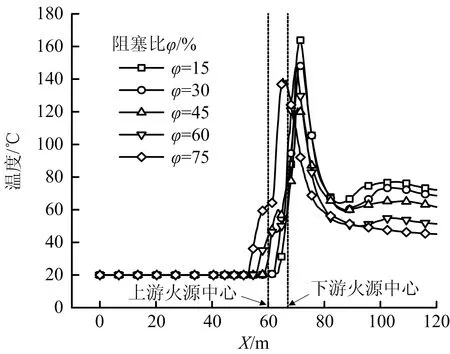
图6 v=3.6 m/s时不同阻塞下顶棚下方0.25 m处纵向中心线温度分布Fig.6 Temperature distribution of longitudinal centerline at 0.25 m below ceiling under different blockage ratios at v=3.6 m/s

2.2 纵向通风风速对纵向温度分布的影响

如图7所示为阻塞比φ=15%时不同风速下纵向中心截面温度分布。由图7可以看出，在小阻塞比条件下，通风对双火羽流行为起主导作用；在较小风速(v=1.2 m/s)时，烟气出现明显的逆流现象，随着风速增加(v=3.6，6.0 m/s)，上下游火源均向下游明显倾斜，没有发生烟气逆流，且上游火源倾斜角度远大于下游火源。

图7 φ=15%时不同风速下纵向中心截面温度分布Fig.7 Temperature distribution of longitudinal center section under different wind velocities at φ=15%

如图8所示为阻塞比φ=15%时顶棚下方0.25 m处纵向中心线温度分布。由图8可以看出，当v≤1.2 m/s，出现2个明显的温度峰值，且火源之间区域顶棚温度较高。当v≥2.4 m/s，只出现1个温度峰值，随着风速的增加，温度峰值逐渐减小，且出现的温度峰值位置逐渐向下游倾斜。

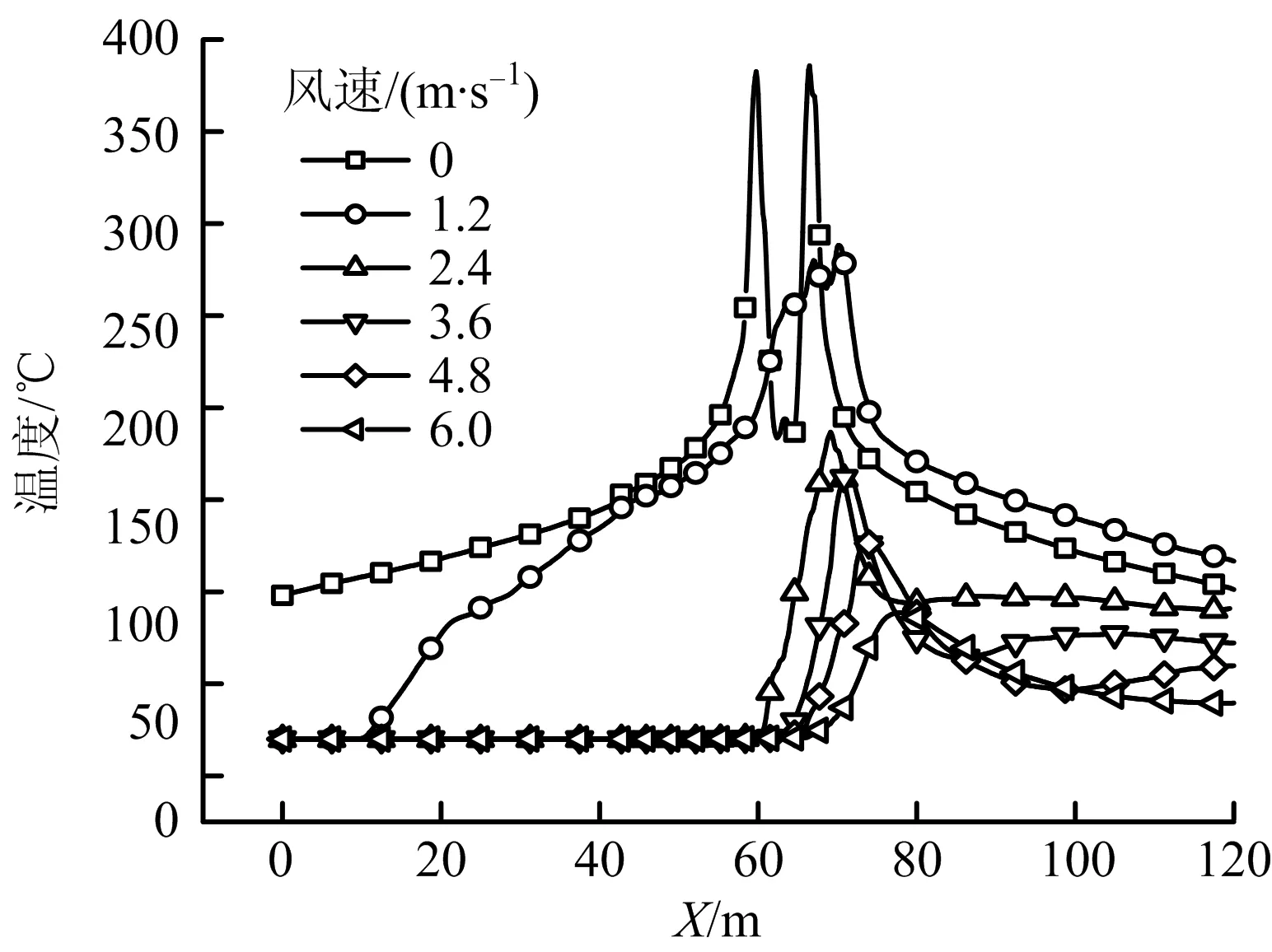
图8 φ=15%时不同风速下顶棚下方0.25 m处纵向中心线温度分布Fig.8 Temperature distribution of longitudinal centerline at 0.25 m below ceiling under different wind velocities at φ=15%

如图9所示为阻塞比φ=60%时不同风速下纵向中心截面温度分布。由图9可以看出，随着风速v增大，烟气逆流现象不再明显，当v≥3.6 m/s，障碍物与上游火源之间出现明显附壁效应，且附壁效应随风速增大越明显。结合图3，图5，图7和图9可以发现，双火羽流的倾斜规律存在与单火源类似的结论，即增加通风速度会降低隧道内温度[7]，且随着阻塞比和通风速度的增加，火羽流倾斜角度从向火源下游倾斜转变为向火源上游倾斜[9]。但不同于单火源的是，双火源条件下，下游火源倾斜方向受阻塞比和通风的影响较小。

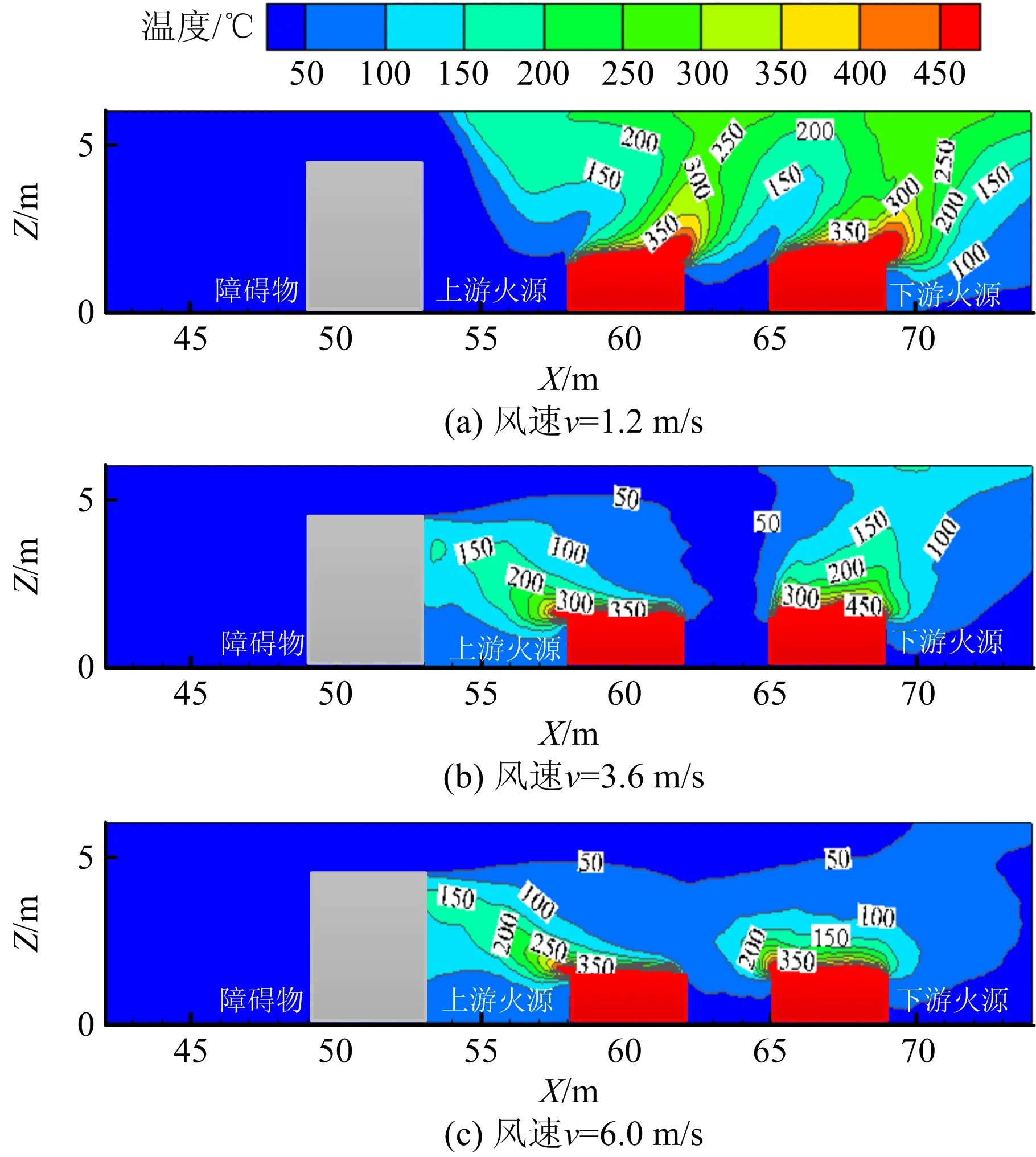
图9 φ=60%时不同风速下纵向中心截面温度分布Fig.9 Temperature distribution of longitudinal center section under different wind velocities at φ=60%

如图10所示为阻塞比φ=60%时顶棚下方0.25 m处的顶棚纵向中心线温度分布。由图10可以看出，与小阻塞比类似，小风速时出现了2个明显温度峰值，随着风速增加，温度峰值变为1个。

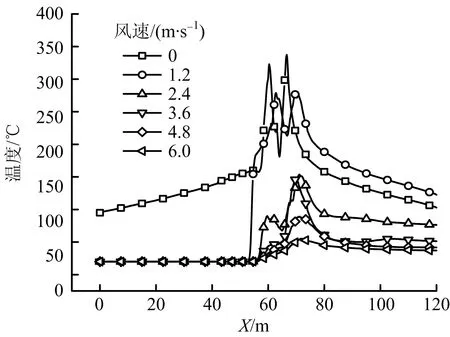
图10 φ=60%时不同风速下顶棚下方0.25 m处纵向温度分布Fig.10 Temperature distribution of longitudinal centerline at 0.25 m below ceiling under different wind velocitie at φ=60%

2.3 顶棚下方最高气体温度分析及建模

图11所示为顶棚下方最高气体温度(Tmax)随纵向风速(v)和阻塞比(φ)的变化。由图11可以看出，随着风速增大，Tmax逐渐减小，且在v≤1.2 m/s时，Tmax均在250 ℃以上，而当v≥2.4 m/s后，Tmax明显减小，均在200 ℃以下。这是因为在风速较大时，会在障碍物后方形成低压区，从而吸引火羽流倾向于障碍物后方，从而导致Tmax迅速降低。此外，同一风速不同阻塞比下的Tmax差异较小，最大差值在50 ℃以内，说明阻塞比对最高温度的影响相对较小。

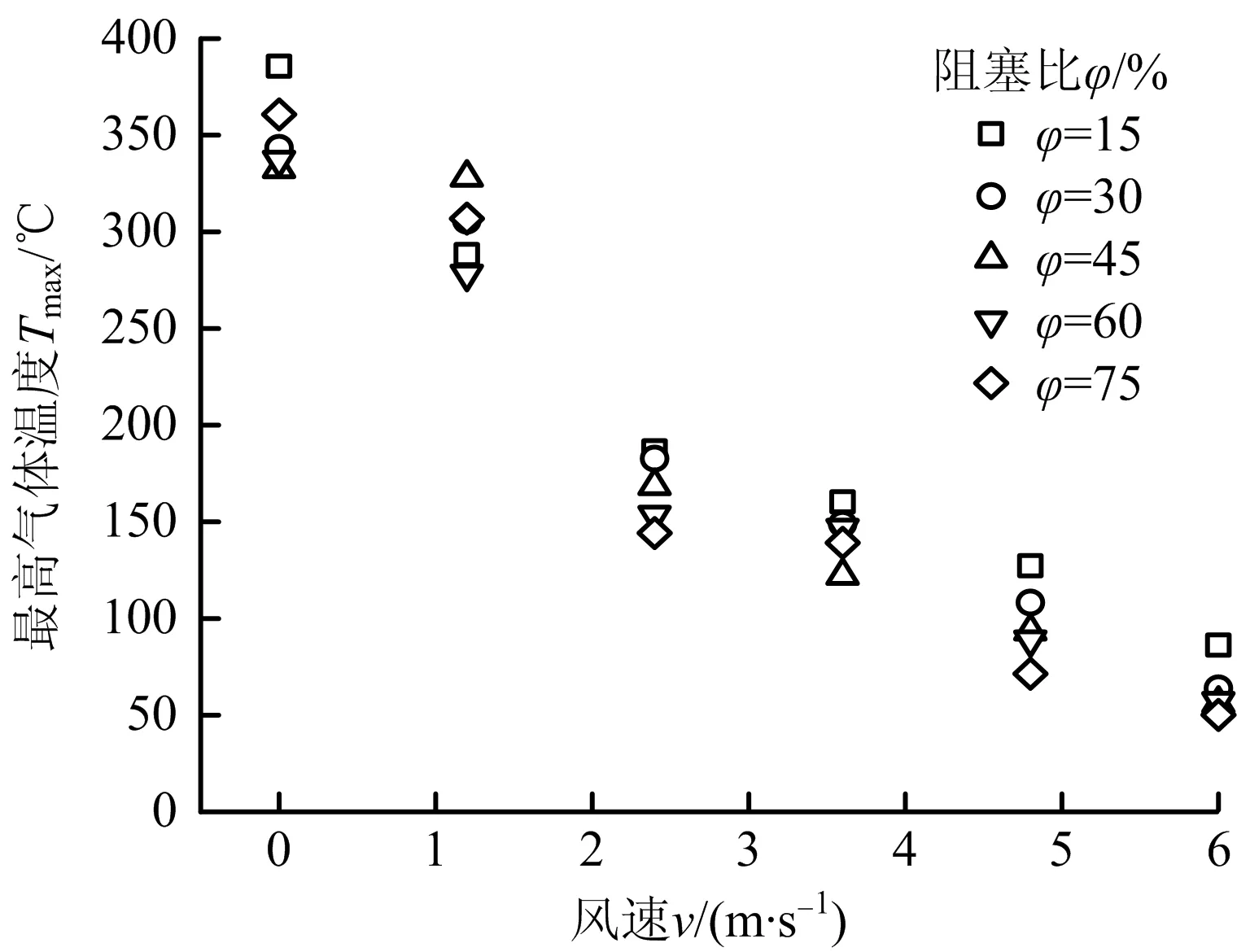
图11 不同工况下顶棚最高温度Fig.11 Maximum ceiling temperature under different conditions

在目前已有研究中，Kurioka等[4]在5个不同尺寸的模型隧道中开展了一系列单火源燃烧实验，得到无障碍物时隧道顶棚下方无量纲最高温升与无量纲火源功率和弗劳德数的经验关系，如式(2)所示：

(2)

需要说明的是Kurioka模型[4]中未考虑阻塞比对最高温升的影响。隧道内存在障碍物时，控制体如图12所示，基于流体力学理论，当空气流体以一定水平纵向通风速度v流经障碍物截面，会在越过障碍物之后速度增大到v′的流体。

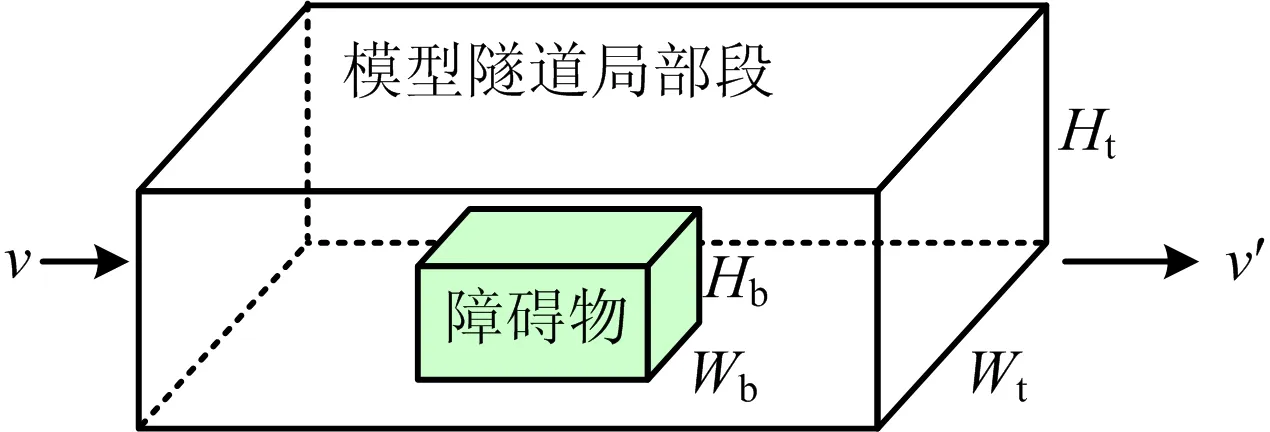
图12 控制体中通风风流越过障碍物前后速度变化示意Fig.12 Schematic diagram of control volume of velocity change before and after the ventilated airflow passes over the obstacle

根据流体质量守恒定律，越过障碍物前后流体的质量流率不变，见式(3)所示：

v·Wt·Ht=v′(Wt·Ht-Wb·Hb)

(3)

式中：Wt和Ht分别为模拟隧道的宽和高，m；Wb和Hb分别为障碍物的宽和高，m。

根据障碍物定义，见式(4)所示：

φ=WbHb/(WtHt)

(4)

由式(3)～(4)得出式(5)：

v′=v/(1-φ)

(5)

借鉴Kurioka模型[4]，将式(2)中的v用式(5)中的v′替换，得到利用阻塞比修正后的弗劳德数如式(6)所示：

Fr′=v′2/(gHd)

(6)

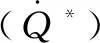
(7)

图13 无量纲最高温升预测模型Fig.13 Prediction model of normalized maximum temperature rise

3 结论

1)相同阻塞比小风速时，顶棚下方0.25 m处纵向出现2个峰值温度，随着风速增大，烟气逆流消失，顶棚最高温度不断降低，温度峰值逐渐变为1个。

2)相同风速下，随着阻塞比增大，下游火源始终向下游倾斜，而上游火源逐渐由向下游倾斜转变为向上游倾斜。

3)基于流体力学理论，引入阻塞比修正无障碍物时弗劳德数Fr数，进而建立适用于隧道内有障碍物情况下的双火羽流顶棚最高温升分段预测模型，模型可为隧道内堵塞条件下顶棚温度预测提供数据支撑和参考依据。