热流涨落稳态涨落定理的检验
毕铭阳,赵 鸿
(厦门大学 物理科学与技术学院,福建 厦门 361000)
1 研究背景
涨落定理的提出是热力学统计物理的重要进展之一.近三十年来,涨落定理受到了人们极大的重视,对涨落定理的检验自然也是人们十分关心的问题.其Evans-Searles涨落定理[1]和Gallavotti-Cohen涨落定理[2]所预言的稳态涨落关系[3]对实际应用具有重要意义,且可以描述流的涨落特性[4].而数值模拟计算非平衡稳态一维晶格模型系统热流比直接计算熵等物理量要简单得多,也更加直观.经过多年的研究,对一维晶格模型的热传导行为已经非常清楚.按照其定性性质,可以把一维晶格模型分为三类,第一类以Fermi-Pasta-Ulam-Tsingou(FPUT)模型为代表,这里实际选取的是FPUT-β晶格模型,该晶格之间的相互作用势函数是非线性的,这类模型虽然是混沌系统,但是其热传导规律不满足傅里叶热传导定律,热传导系数随系统尺寸增加而发散[5].第二类以Ф4晶格模型为代表,同样是混沌运动的系统,但是其热传导规律符合傅里叶热传导定律,也就是具有正常的热传导行为.第三类是简谐振子链模型,它代表完全可积的系统,不具有混沌运动,热传导规律也不满足傅里叶热传导定律.本文将对这三类系统的热流涨落进行研究,通过大规模数值计算详细检验它们是否满足涨落定理.
在热流涨落检验稳态涨落定理方面,Lepri等首先在1997年采用全局平均热流来表示熵产生,给出了一个使用一维FPUT-β模型的验证结果[8].两年之后,Sano则使用了一维晶格ding-dong模型并采取了同样的全局平均热流到熵产生的转化关系进行了验证[9].这两个工作的结果显示热流的涨落符合稳态涨落定理的预言.1999年,Lepri和Rondoni通过研究周期性Ehrenfest风树模型这个非混沌但是较为复杂的模型的弛豫过程的动量流来验证稳态涨落定理,发现即使是非混沌的模型也依然可以符合稳态涨落定理的预言[10].2000年,Searles和Evans将涨落定理应用到非平衡态动力学系综,验证了暂态涨落定理在所有平均时间下都可以得到满足,而稳态涨落定理只有在长时间的平均下才能得到满足的结论[11].2005年Evans、Searles和Rondoni的工作表明对于一类处于平衡态或近平衡态的多粒子系统,在平衡态和近平衡态的情况下,相空间收缩率不满足稳态涨落定理,其误差会随着系统远离平衡态而减小,恰当定义的耗散函数则在平衡态和非平衡态都可以满足稳态涨落定理[12].Dolowschiak和Kovacs在2005年的工作表明Nosé-Hoover热源下的洛伦兹气体的相空间收缩率在近平衡违背稳态涨落定理,而熵增率则在近平衡和远平衡都满足稳态涨落定理[13].Coretti和Rondoni在2020年的工作显示,暂态和稳态涨落关系都可以在不反转磁场的情况下从均匀稳定的磁场中推出[14],随后在2021年的工作中通过数值模拟在非零磁场中的真实液态氯化钠模型验证了暂态涨落关系[15],2021年Li,He通过路径积分法和大偏差定理推导了广义涨落定理和长时间极限下的环境熵产生涨落定理,对于FPUT-β模型[16]和Ф4模型[17]的研究发现主泛函在有限平均时间窗口下满足稳态涨落定理,而总熵产生在有限平均时间窗口下不符合,环境熵产生随平均时间窗口的增大逐渐符合稳态涨落定理.另外还有一些直接的实验验证工作,如在2004年Ciliberto等人研究两个对转圆盘之间旋转产生的冯卡门涡流和风洞射流的动量输运验证了稳态涨落定理[18],2005年Shang等人通过激光多普勒测速法测量柱状容器中的湍流性质的瑞利贝纳德对流验证了稳态涨落定理[19]以及2018年Hoang等人通过光镊高精度测量空气中光学失重的纳米微球的瞬时位置和速度验证了包括微分涨落定理,广义Jarzynski等式等不同涨落定理的工作等[20].
然而这些研究还没有明确回答什么样的系统其流涨落满足稳态涨落定理,特别是对于上述三类系统,稳态涨落定理是否都能满足,以及在什么条件下满足,以及稳态涨落定理应用到这些系统时有什么不同表现等.本文将遵循Lepri等提出的方案,通过细致的数值模拟回答这些问题.具体来说,假设流经一维晶格第i个格点粒子的热流为ji(t),以t时刻流经N个粒子的平均热流,
(1)
为研究对象,考察给定长度为t的时间窗口内热流的时间平均值Jt,
(2)
的涨落性质,数值检验稳态涨落定理[8]
(3)
是否被满足,以及对模型、系统尺寸、温差、观测时间窗口等的依赖关系.上式中,z=Jt/J∞为相对热流,J∞为稳态热流,Pt(z)为在平均时间窗口为t的情况下,相对热流为z的概率.
为了便于与理论预言的直观比较,我们将(3)式右边的稳态热流、温差项和平均观测时间除到左边,并定义
(4)
这样,涨落关系的检验就表现为检验F(z)和z的斜率是否为1且满足线性关系.
2 模型介绍
考虑一个有N+2L个粒子的一维晶格模型系统,其中,位于中间的N个粒子是我们的主要研究对象,而在这N个粒子的两侧每侧各有L个粒子扮演热源的角色.我们用xi来表示第i个粒子远离平衡位置的位移,并且在固定边界条件x1=xN+2L=0下进行研究.系统的哈密顿函数可以写成
(5)

作用于第i个粒子上的力由(6)式计算.
fi=-(V'+U').
(6)
系统的运动方程为
(7)
(8)

(9)
其中,为了得到非平衡稳态热流我们在左右两侧的热源施加不同的温度TL和TR(TL>TR),这里采用的是朗之万热源,γ为热摩擦系数(本文固定γ=1),ηL,R是均值为0的高斯白噪声项,满足<ηL,R(t)ηL,R(t')>=2γL,RTL,Rδ(t-t').
Lepri等人[8]在1998年的文章中采用了如下的热流定义:
(10)
其中ji表示流经第i个粒子的热流,a为晶格常数,本文中固定为a=1.本文的数值验证采用这个定义,不过我们也计算了其他定义下的情况,发现定性而言结论没有差别.
3 数值结果
我们首先给出涨落关系随着平均时间增加的检验结果.图1给出系统尺寸分别取为N=32和N= 512,平均时间t=2,5,10,30,50,100下的下F(z)和z的依赖关系. 热源温度TL=0.55,TR=0.45.


图1 观测时间窗口对稳态涨落定理的影响.(a)、(b)为FPUT-β模型, (c)、(d)为简谐振子链模型, (e)、(f)为Φ4模型.从上到下时间窗口依次增加,虚线代表稳态涨落定理预言的理论值.
图1的结果表明,无论是N=32还是N=512的情况下,三类模型在t较小的情况下,结果偏离涨落定理的预言,而随着平均时间t的增大,结果逐渐靠近涨落定理的预言.这与涨落定理所要求的t趋于无穷时成立相一致.因此,在Lepri等所定义的流涨落下,稳态涨落定理对于三类模型都成立.
比较N=32和N=512的结果可以发现,在相同的时间测量窗口下,系统尺寸越大与涨落定理的预言偏离越大.在尺寸较大的情况下,Φ4模型收敛最快,其次是FPUT-β模型,简谐振子链模型收敛最慢,在t=100的时间窗口下图中F(z)的斜率与理论预言的斜率尚有接近1倍的差距.进一步的计算表明t>500后结果收敛于理论值.为了展示尺寸依赖性,我们以FPUT-β模型为例分别计算了t=2和t=50情况下涨落关系随系统尺寸的变化,如图2所示.可见与涨落定理的理论预测值的偏离随着尺寸的增加而增加.

图2 系统尺寸对稳态涨落定理的影响(FPUT-β模型).从下到上N依次增大,虚线代表稳态涨落定理预言的理论值.




图3 有限时间窗口下涨落关系随系统尺寸存在标度率.(a)、(b)为FPUT-β模型, (c)、(d)为简谐振子链模型, (e)、(f)为Φ4模型的结果.

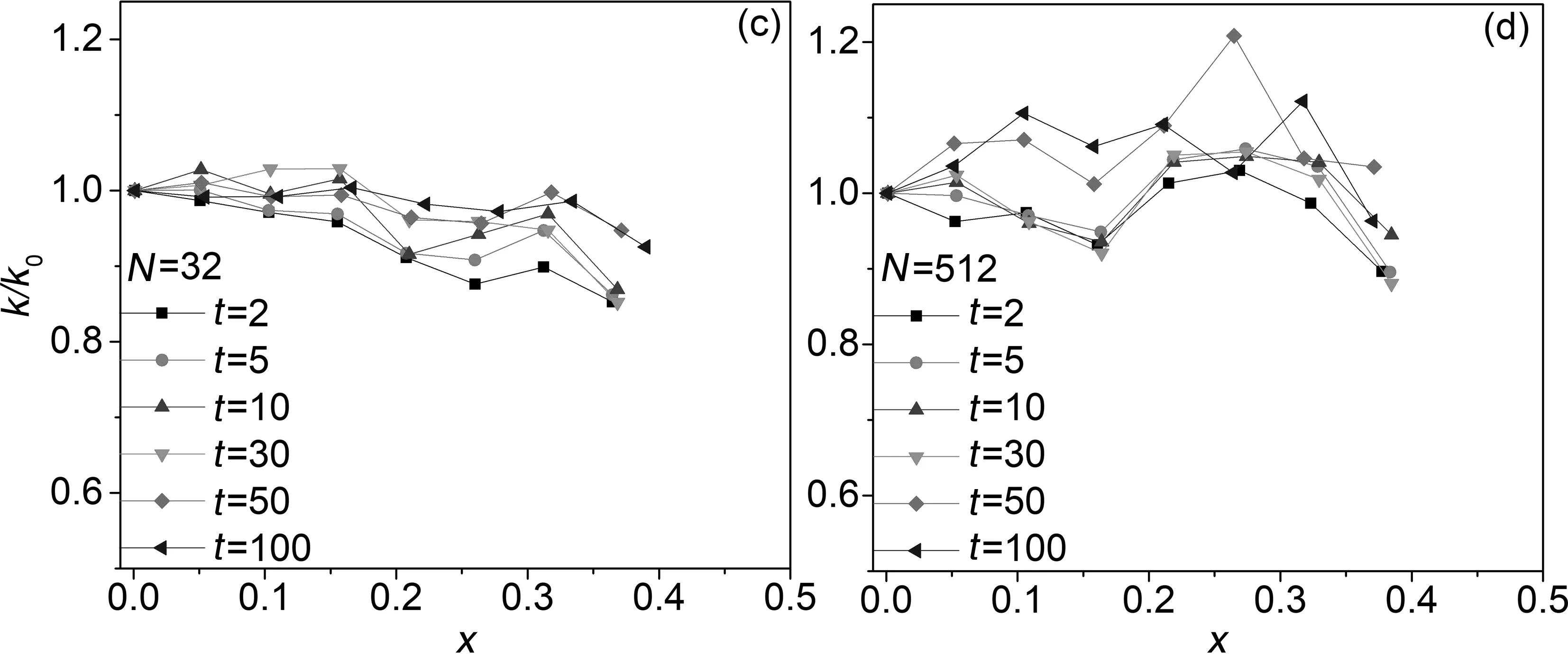
图4 涨落关系与线性的偏离.(a)、(b)给出t=2和t=50情况下非线性效应随N的变化,(c)、(d)给出N=32和N=512情况下非线性效应随t的变化.
最后我们探究了热源温差对涨落关系的影响.图5中,我们给出了FPUT-β模型在系统尺寸N=32,平均时间窗口t=2和t=50的情况下保持热源平均温度为T=0.5不变,改变热源温差△T=0.05,0.1,0.2,0.3,0.4的结果.可见在保持热源平均温度不变的情况下,改变热源的温差并不会显著地改变涨落关系.不过我们的结果也表明随着温差的增大涨落关系向理论预言值趋近,这个结论和文献[16]中的结论是一致的.

图5 热源温差的影响.系统尺寸固定在N=32.温差由上向下依次增加
4 总 结
我们通过数值模拟对三类具有代表性的一维晶格模型的热流涨落的稳态涨落定理进行了验证,表明在平均时间窗口趋于无穷时此定理都严格成立.这三类模型中包括本身完全可积因此非混沌的简谐振子链模型,这表明稳态涨落定理所需要的混沌性假设并不一定要求系统本身是混沌的,当这类系统和热源连接后其所需随机性可以由热源提供,这应当是稳态涨落定理能适用于非混沌系统的原因.本文发现当时间窗口较小的情况下,或者一般地在远离涨落定理理论预言的区域,涨落关系对系统尺寸的依赖存在一个标度率.有趣的是这个标度因子刚好是一维晶格不同尺寸系统热传导系数的比值.这一现象表明了不同尺寸的系统涨落关系之间存在一种普适规律,且和热传导系数有关,但是其深刻的含义还有待进一步详细研究.本文还研究了涨落关系的非线性偏离问题,发现随着系统尺寸增大或时间窗口增大这种效应都会迅速消失,因此至少对热流涨落稳态定理的影响不重要.我们也研究了热源温差的影响,发现温差越小对稳态涨落定理的偏差越大,这印证了之前文献中的相关结论.

