改进蚁群算法下的车间物料配送路径规划研究

杨雷博，周俊

(上海工程技术大学 机械与汽车工程学院，上海 201620)

0 引言

随着客户个性化定制的兴起，多品种、小批量的混流生产日渐成为满足市场需求的重要途经[1]，混流生产是一种在同一条生产线上对多种产品进行生产的生产方式，在混流生产过程中物料配送效率的高低会直接影响到物料配送周期、生产节拍、库存水平等，较高的物料配送效率会为混流企业带来巨大的效益，节约大量的成本。而提高效率的关键一环就是要对物料配送的路径进行研究，因此对车间物料配送路径的研究是非常有必要的。

目前对车间物料配送路径规划方面的研究有很多，文献[2]针对不确定因素进行考虑，建立了机会约束规划模型，并提出了一种改进的传统混合智能算法，最后用该算法对模型进行了求解；文献[3]以车辆路径规划问题(Vehicle Routing Problem，VRP)基础，建立了物料配送路径规划模型，并对蚁群算法做出了改进，用改进的蚁群算法对模型进行了求解；文献[4]针对行驶时间区间不确定的路径问题提出了将不确定行驶时间由区间数表示，并借助鲁棒优化的方法，建立了装配线路径规划模型，最后设计了一种混合遗传算法求解此模型；文献[5]设计了一种双层递进的进化优化算法，并根据问题建立了以配送距离最短、配送次数最少和车辆利用率最大为优化目标的物料配送路径模型，最后用设计的算法对模型进行了求解；文献[6]对粒子群优化算法进行了改进，并用改进的算法求解了以物料配送路径最短的优化目标模型；文献[7]针对农用机械混流车间配送路径规划难、线边库存高的问题，设计了以小车配送距离最短和线边库存最小为优化目标的规划模型，根据实际布局设计栅格环境地图，并通过改进的蚁群算法对模型进行了求解；文献[8]考虑了离散型车间余-废料回收率低、成本高的问题，针对这个问题建立了一个物料再循环的路径优化问题模型，最后借助遗传算法求解了问题模型。

综上所述，以上研究虽对问题模型都取得了较好的解，但在实际的混流车间生产过程中，由于工位布局的影响，实际的配送距离会大于两点距离公式计算的距离，而距离对小车的配送时间又会有巨大影响，为使实际的配送距离最短就需要考虑在各需求点时间窗约束下的实际车间布局，而以上研究并没有将混流车间工位的实际布局和时间窗因素进行有效的结合，因此为更好的解决混流车间物料配送在时间窗约束下的路径规划问题，本文将借助栅格化后的车间布局栅格地图[9]，通过对蚁群转移规则和信息素更新规则进行改进，并用改进后的蚁群算法对模型进行求解，使达到配送路径最短，所用配送小车数量最少，实现配送成本最低的优化目标要求。

1 模型建立

车间物料配送问题是一种结合实际车间布局的VRP问题[10]，本文由最短配送距离和最少车辆使用数目确定出最小配送成本，并以此为优化目标，同时考虑各工位的实际需求和时间窗约束建立数学模型。模型假设配送小车有m辆，配送点有n个，小车从物料仓库装载后出发，依次在合理的约束下对每个配送点进行配送，直到小车空载后再次回到物料仓库，至此一次配送结束。此外，在建模前需要满足以下相关假设：

1）单车运载力要大于单个配送点的需求量。

2）配送中心能够满足所有配送点需求，无缺货。

3）车辆完成配送后直接返回配送中心。

根据以上条件建立问题模型：

设i、j为需求点，其中i=0或j=0为物料仓库；k为配送小车；xijk为小车k由需求点i到需求点j；Sij为需求点i到j的距离；Ca为单位配送距离的成本，Ca=1；Cb为每辆车的成本，Cb=1000；yik为需求点i由小车k配送；ai为需求点i所需物料的数量；vi为需求点i单位物料体积；li与ri分别为需求点i的左时间窗和右时间窗；tik为小车k到达需求点i的时间。

优化目标：

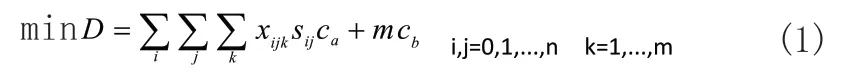
相关约束：

上述优化模型中，式(1)表示优化目标；式(2)表示一个需求点由一辆小车配送；式(3)～式(5)表示对所有需求点的配送，且需求点都只能被配送一次；式(6)表示小车的限载量；式(7)表示时间窗要求；式(8)～式(9)表示变量之间的关系。

2 基本蚁群算法

蚁群算法最早是由Dorigo提出来的[11]，它的基本思想是通过一群人工蚂蚁相互协作来完成最优解的寻找，每只人工蚁按着一定的转移规则选择相应的移动目标点，并在移动过程中释放信息素，人工蚁通过信息素交换信息，从而达到相互协作的目的。蚁群算法中τij为信息素浓度；nij为能见度因素；α为启发因子；β为期望因子；P为信息素保留因子；Δτij为信息素增加量。以下为基本蚁群算法的算式[12]：

其中式(10)表示蚁群的转移规则；式(11)～式(12)表示信息素更新规则；式(13)表示蚁周系统模型。

3 改进蚁群算法

蚁群算法因为是一种正反馈算法，在算法的计算过程中，如果有一个解一直为最优，则算法就很容易的陷入到局部最优解中，为防止算法陷入局部最优。主要对算法进行以下改进。

3.1 状态转移规则的改进

转移规则决定着蚂蚁下一步的走向，蚁群算法只考虑了信息素浓度和启发函数两种因素，而在实际的车间物料配送中，由于配送点的物料服务需求时间窗约束对蚂蚁的选择也会造成一定的影响，时间窗越窄表示配送点对物料的需求越紧迫，小车等待时间过长也会造成配送效率的下降，因此本文选择在状态选择规则中加入等待时间(wait)和时间窗宽度(width)两种因素[13]，对规则进行优化。改进的转移规则如下：

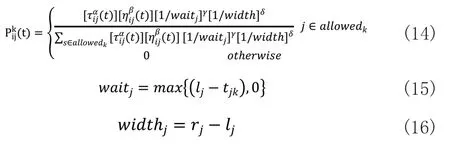
式中γ、δ分别为等待时间因子和时间窗宽度因子。式(14)为改进的蚁群转移规则；式(15)为小车的等待时间；式(16)为需求点的时间窗宽度。

3.2 信息素更新规则的改进

为了防止算法陷入局部最优解，出现搜索停滞，本文引入了遗传算法中的变异算子和信息素平滑机制来提高算法的搜索能力。在改进之前首先要对物料仓库和配送点进行自然编码，用0表示物料仓库，用1,2,...n表示物料需求点，m辆小车从物料仓库出发对n个物料需求点配送，在满足约束的情况下配送完回到物料仓库，形成相应的配送路径,其路径表示(0,x1,x2,...xs,0,xi,...xk，0,...)。

3.2.1 变异算子

在所有蚂蚁都形成各自的配送路径后，分别对各个蚂蚁的路径按一定概率进行变异，具体步骤如下：

1）首先，随机产生一个变异概率，并与设定值作比较，大于设定值进行变异，否则不进行。

2）变异点确定：随机选取一个当前路径中的点，以(123456789)为例，选取第四位为变异点，此时路径为(12356789)。

3）将2中选取的变异点随机插入到当前路径中，例如插入第六位与第七位之间，形成变异后的路径为(123567489)。

4）验证变异后的路径是否符合约束。

5）将变异后的路径和变异前的路径作比较，并保留最优路径。

6）按照上述步骤完成所有蚂蚁的路径变异，则变异结束。

3.2.2 信息素平滑

由于蚁群算法具有依靠信息素浓度选择的正反馈机制，经多次迭代后蚂蚁都会集中到一条当前最好的路径，此时这条路径上的信息素浓度最高，而其它路径上的信息素浓度就偏低，这样算法一旦陷入局部最优解就会很难跳出来。为防止此种现象出现本文引入了信息素平滑机制[14,15]对算法进行改进，如果连着多次迭代的最优解都相同，则借助以下公式对信息素进行平滑：

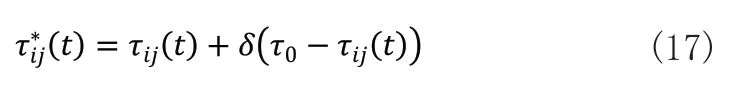
其中为平滑后的信息素浓度；τij(t)为平滑前的信息素浓度；δ(0<δ<1)为平滑程度控制参数。改进的蚁群算法流程：首先设置参数并初始化，然后构造每只蚂蚁的路径，构造完成后对路径进行变异，并判断变异是否有效，接着进行信息素全局更新，判断N次最优解是否有变化，没变化就进行平滑，最后判断是否满足终止条件。具体如图1所示。

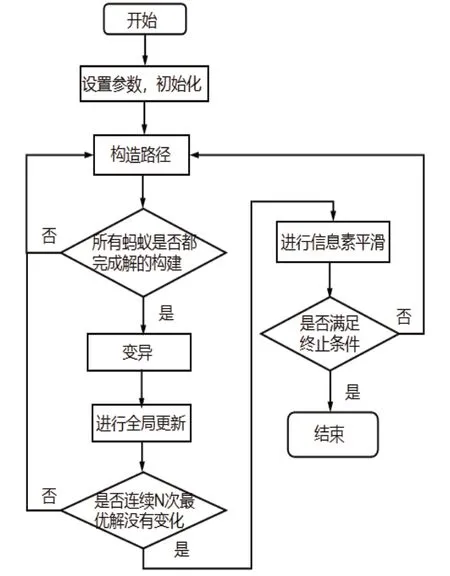
图1 改进后的蚁群算法流程图

4 案例分析

为检验算法的可行性，并评估改进后算法的优越性，本文选取了某发动机装配车间为实例进行验证。该车间按照物料管理要求，可将距离和工艺要求以及时间窗相近的工位点进行整合，最终形成9个工位组。根据生产计划可得到各工位组一天的物料需求和对应时间窗。如表1所示，其中0为物料仓库；1～9为工位组。

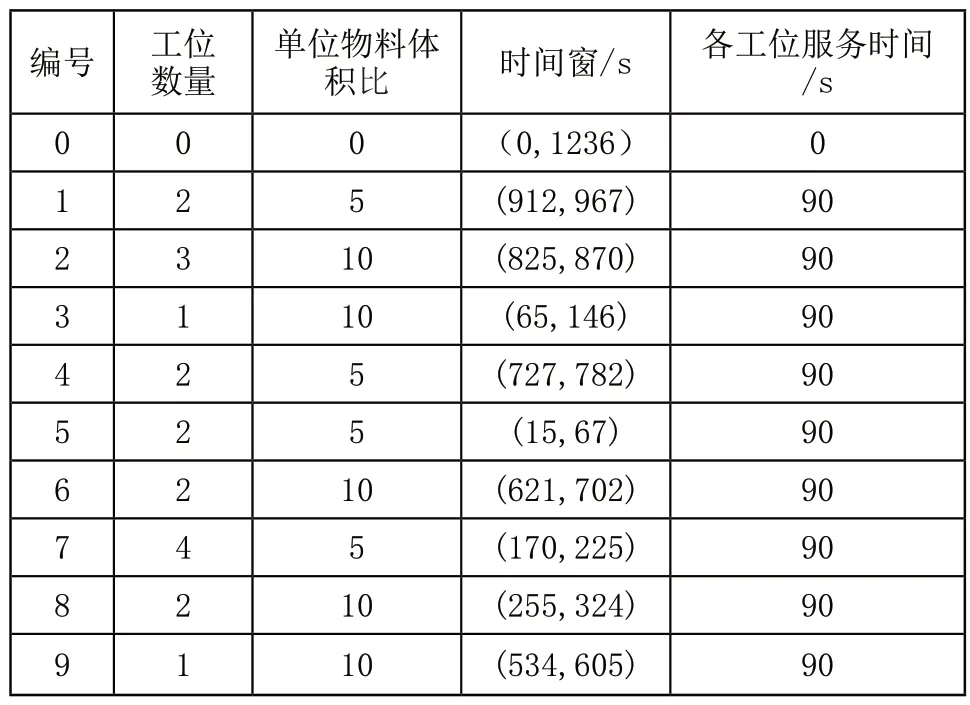
表1 各工位组物料需求

在实际的混流车间中由于受到道路和工位布局的影响，配送路径并不能按照两点公式进行计算，这就会使得实际的配送路程远远大于理论值。因此为更好反应实际情况本文采用栅格化后的车间布局图，将布局分为可行区域和不可行区域，其中白色为可行区域，黑色为不可行区域，并设定每小格边长为10米。栅格化后的地图如图2。在图2的基础上由蚁群算法分别计算出物料仓库到各工位组以及各工位组之间的最短路径距离，最终可获得各工位组相对距离表，第一列和第一行为工位组，0为物料仓库。具体如表2，其中第一行、第一列为物料仓库和工位组，中间数据为相对距离。

图2 车间布局栅格图

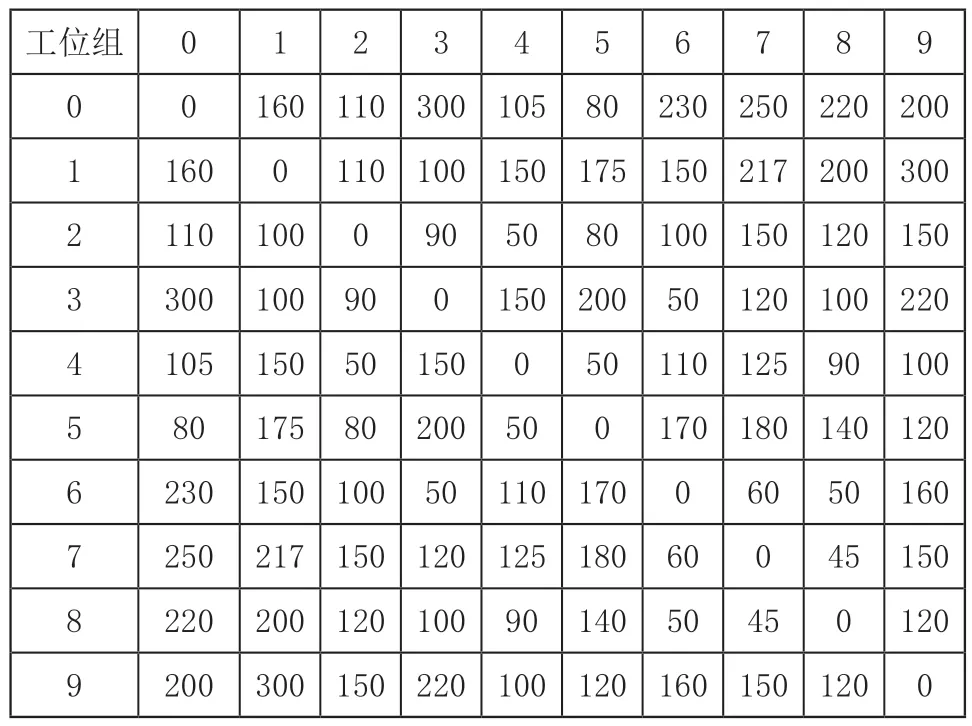
表2 物料仓库和各工位相对距离 (m)

在MATLAB R2018a平台上实例计算，参数设置分别为α=1，β=3，γ=3，δ=3，蚁群数量为50，最大迭代次数为100。将基本蚁群算法和改进蚁群算法(式14)在平台上分别运算10次，得到在各自算法下的最短配送总距离，如表3所示。

从表3结果的对比中能发现，在10次运算中算法改进后较改进前平均距离减少了65.5m，其中基础蚁群算法的最短距离为1365m；改进蚁群算法对应最短距离为1335m，改进前后最优路径距离缩短了30m。

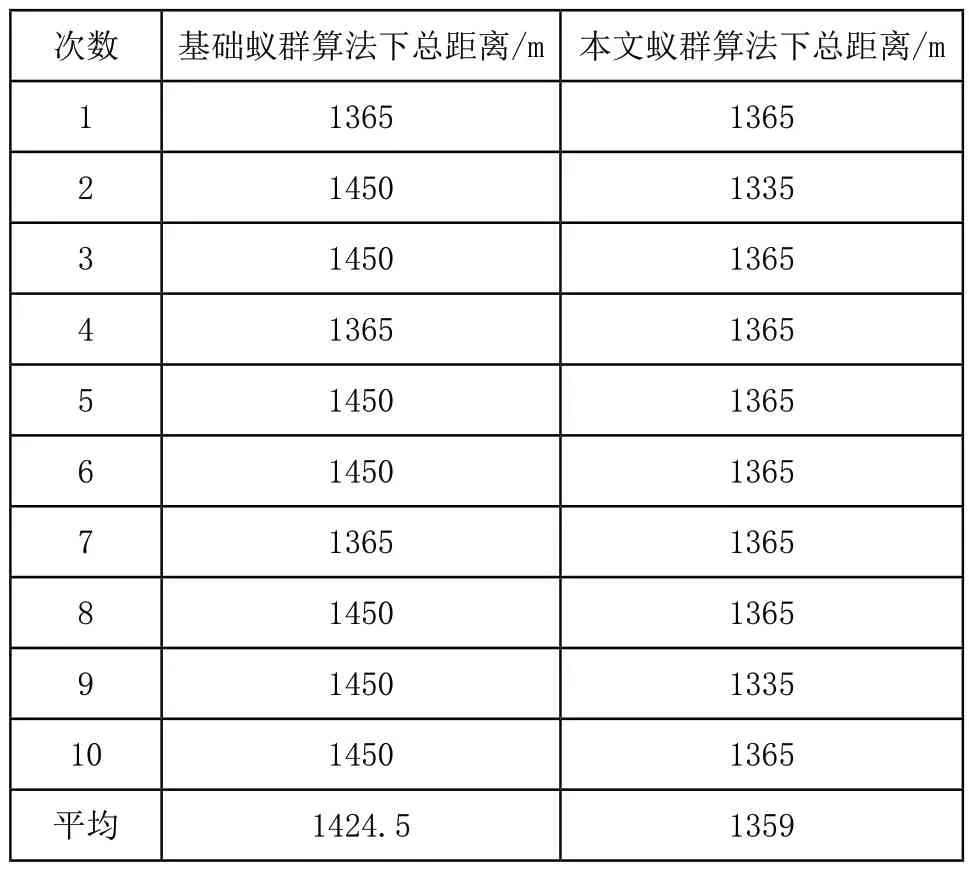
表3 两种算法下的总配送距离

如图3、图4所示，分别为基本的蚁群算法和改进的蚁群算法的迭代曲线。

图3 基本蚁群算法的迭代曲线

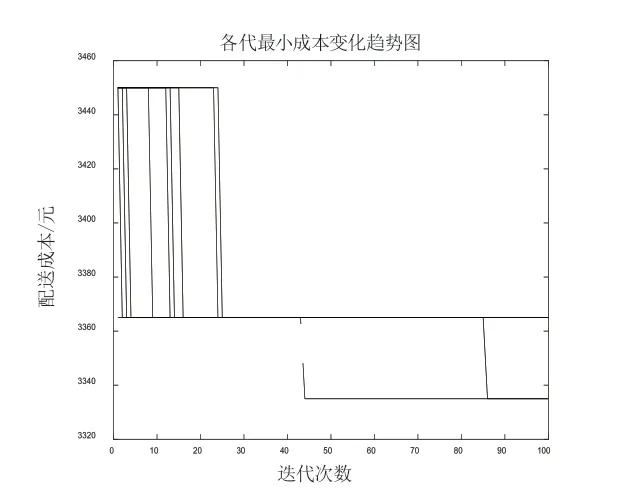
图4 改进后的蚁群算法的迭代曲线

优解，出现搜索停滞，相比基本蚁群算法的最优解，改进的蚁群算法最低成本降低了30。在所需最小车辆数目为2的条件下，这两种算法对应各自的最优配送路径为：

基础蚁群算法：第一辆，0-5-3-6-4-2-1-0；第二辆，0-7-8-9-0。

改进的蚁群算法：第一辆，0-3-7-8-6-4-2-1-0；第二辆，0-5-9-0。

由此说明了本文的蚁群算法对模型的求解具有良好的性能。

5 结语

本文针对混流生产车间物料配送的准时化，路径的多样化问题，建立了混流车间的物料配送路径优化模型，并对蚁群算法中的转移规则和信息素更新规则进行了改进，使得算法在符合物料配送实际情况的同时也提高了算法的全局搜索能力。最后结合实际案例分析结果表明，改进算法能收敛到更好的解，与基础的蚁群算法相比改进蚁群算法配送成本更低，为制造企业进行车间物料配送路径规划提供了参考。