基于改进模糊—熵权数控磨床可靠性分配优化研究

范晋伟，刘会普*，秦池，李伟华

（1.北京工业大学 机械工程与应用电子技术学院，北京 100124；2.北京第二机床厂有限公司，北京 102444）

0 引言

数控磨床广泛应用在汽车、飞机等行业精密零件的加工中，通常作为最后一道工序的加工设备，其可靠性的高低对零件的加工质量和生产效率均有重要影响[1]。中高档数控磨床可靠性的提升，依靠于各个子系统可靠性的提升，但如何将数控磨床整机的可靠性指标分配到各个子系统，这就需要对可靠性分配方法进行研究。

国内外学者对可靠性分配方法进行了大量的研究工作：王保帅等人结合层次分析法和群体决策法对智能电表的可靠性分配进行了研究[2]。隆萍等人利用等分配法、比例组合法和评分分配法对风力发电机组进行了可靠性分配的研究[3]。陈一凡等人基于元动作理论建立了数控转台的可靠性分配模型[4]。Z Yang等人基于Gumbel Copu-la函数及Kendall相关系数建立了失效系数矩阵，对数控车床主轴系统进行了可靠性分配[5]。Omkarprasad等人以系统成本最小为目标，建立了串联系统成本最小化可靠性分配模型[6]。以上可靠性研究方法为机械系统可靠性分配方法提供了参考，但目前机械系统可靠性分配方法依旧存在以下关键问题需要进一步探究：

1）现有机械系统可靠性分配方法多以电子系统可靠性分配方法为基础，忽略了两种系统在结构上的差异。

2）可靠性影响因素打分标准多以专家意见为主，缺乏对客观故障信息的评估，使机械系统可靠性分配结果带有明显的主观性。

针对以上问题，文章提出了一种基于改进模糊综合评价法和熵权法的可靠性分配方法，以数控磨床平可靠度R大于0.9和平均故障间隔时间MTBF大于2000h为设计标准，对各个子系统进行可靠性指标分配。该方法将机械结构作为评估标准之一，以模糊综合评价法和熵权法为理论基础，充分利用了主观和客观两个方面故障信息，实现了对数控磨床既定可靠性指标的预分配，为可靠性分配优化工作提供了新的思路。

1 基于改进模糊-熵权的可靠性分配模型

1.1 基本理论

1）模糊综合评价法；模糊综合评价法是一种基于模糊数学的综合评价方法，其核心是模糊数学中的隶属度理论，它能把定性评价转化为定量评价，即用模糊数学对受到多种因素制约的事物或对象做出一个总体的评价[7]。该方法具体操作步骤如下：

（1）确定评价因素集合U

设评价因素集合U={u1,u2,...,un}，集合中ui表示第i层评价因素。

（2）确定评价等级标准集合V

设评价等级标准集合V={v1,v2,...,vn}，集合中vi表示第i个评价元素分值。

（3）确定隶属度矩阵

设隶属度矩阵R={ri1,ri2,...,rij}，rij的取值在0到1之间，该值表示vj在因素ui中的特征比。

（4）多层次综合评价

根据评价对象具体情况，选择最适合的评价等级，在遵守最大隶属度原则的基础上，得出较为客观的评价结论。

2）熵权法；熵这个概念源于热力学，指标的信息量越大，信息熵值越小，所确定的权重越大，熵权法是一种常用的客观赋权方法，通过建立原始数据评价矩阵计算出各指标权重，与主观赋权法相比较，熵权法客观性强，同时有着较高的精度［8］。熵权法计算权重的具体过程如下：

（1）建立原始数据评价矩阵K

其中，kij为指标初始评价值。

（2）归一化矩阵K获得矩阵L

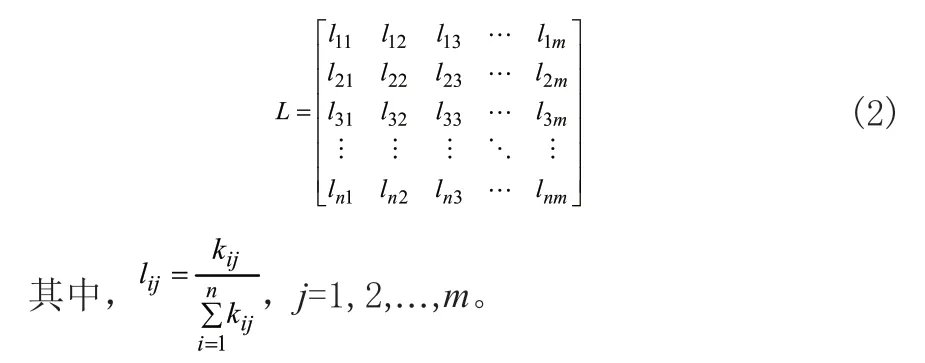
（3）计算信息熵ej

其中，ej为第j项指标的熵值；为信息熵系数。

（4）计算熵权βj

其中：βj为第j项指标的熵权。

3）改进模糊-熵权评价法；为充分利用故障数据信息价值，克服模糊综合评价法中评价等级依赖专家打分而造成主观性过强的缺点，因此文章提出一种改进模糊—熵权评价法，该方法基于机械结构和故障数据构建了可靠性影响因素矩阵K，并将其作为评价矩阵进行熵权值计算。该方法具体操作步骤如下：

（1）建立可靠性影响因素集K

K={k1,k2,k3,k4}={故障频数比，维修时长比，可靠性影响度，结构复杂度}。

其中，故障频数比为某一子系统发生故障数与总故障数之比，该值的大小能客观反映各个子系统的相对稳定水平；维修时长比为某一子系统发生故障停机维修所需时间与所有维修所需时间之比，该值的大小能客观反映子系统维修难易程度；可靠性影响度为整机可靠度与某子系统的可靠度之比，该值的大小能客观反映该子系统可靠度对整机可靠度的影响水平；结构复杂度为某子系统零件数量与整机零件数之比，该值的大小能客观反映该子系统结构难易高低。

（2）建立影响因素隶属度矩阵M

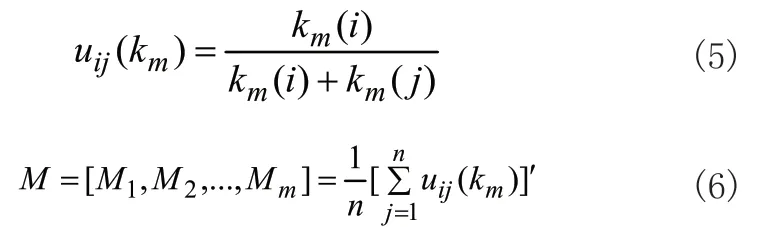
其中，uij(km)表示子系统i与j相比，子系统i对因素km的相对隶属度；km(i)表示在因素列向量中第i个元素。

（3）熵权法求综合影响度

将影响因素隶属度矩阵M代入式(2)～式(4)，计算得到各个子系统可靠度的综合影响度。

1.2 改进模糊-熵权法可靠性分配优化流程图

基于改进模糊-熵权法数控磨床可靠性分配优化方法的流程图如图1所示。

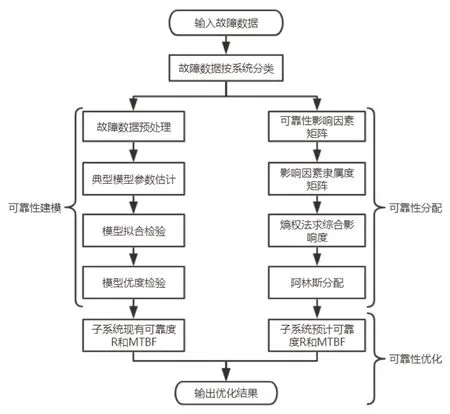
图1 数控磨床可靠性分配优化流程图

1）可靠性建模：该部分包括故障数据预处理、参数估计、拟合检验和优度检验，通过以上步骤可确定各个子系统故障数据的分布模型，进而确定子系统现有可靠度R和平均故障间隔时间MTBF。

2）可靠性分配：该部分计算数控磨床子系统可靠性影响因素矩阵、隶属度矩阵和综合影响度，以整机可靠度R=0.9和MTBF=2000h为设计条件，通过阿林斯分配获得分配后达到的可靠度R和MTBF。

3）可靠性优化：该部分计算子系统现有可靠度R和MTBF与预计值之间的误差，建立可靠性优化强度函数P(t)确定子系统可靠性优化的先后顺序。

2 可靠性建模

可靠度R和平均故障间隔时间MTBF是机械系统可靠性分配的重要指标，两者的点估计结果基于对故障信息的可靠性建模分析。

2.1 故障数据分类及预处理

文章的可靠性数据来源于北京第二机床厂同一型号数控磨床现场实验数据及厂家实际生产过程中记录的数据，在严格遵守《数控机床可靠性评定》中相关原则[9]前提下，共获得404条真实可靠的故障数据。考虑到数控磨床是典型的机电液一体化设备，其设计、制造、外协及装配工作将分化到各个子系统进行，故将故障数据也分类到每个子系统，方便各个子系统进行可靠性分配。分类结果如表1所示。

表1 数控磨床故障数据分类表

在可靠性数据分类后，为了便于研究各个子系统可靠度的分布类型，需要将子系统故障数据进行预处理，可靠度的估计值可用中位秩计算[10]，可靠度函数R(ti)计算公式如下：

式中，n—故障总数

ti—第i个故障间隔时间

F(ti)—ti时间之前的累积失效概率

2.2 参数估计

利用式(7)和式(8)可建立起各个子系统故障间隔时间ti与可靠度R(ti)之间的对应关系，常用最小二乘法进行故障模型参数估计，典型分布模型参数估计公式如表2所示。

表2中，a0和a1为线性相关式y=a0+a1x的系数，可由最小二乘法[11]线性回归得到，相关公式所示：

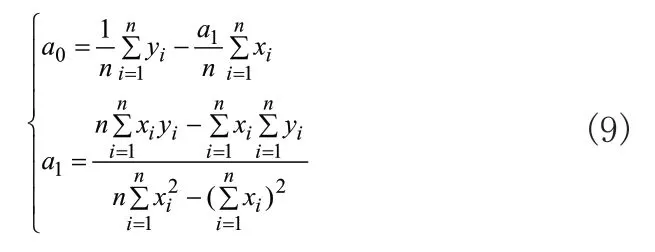
表2 典型分布函数参数估计表

2.3 假设检验

利用式(9)和表2可求解出各个子系统故障数据对应典型分布函数的拟合参数，由于典型分布模型在局部区域具有相似性，很难确定各个子系统故障数据更适合哪种分布类型，需进行假设检验。常用D检验法[11]进行假设检验，相关公式如下：

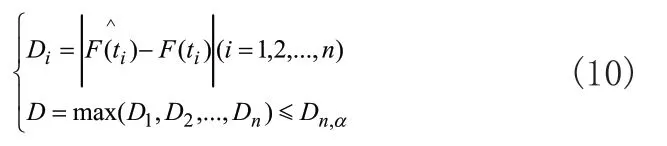
表3 Dn,α经验公式表

2.4 优度检验

当子系统的故障数据同时符合两种或两种以上分布模型时，需要对分布模型进行优度检验。常用相关系数法[12]来进行模型优度检验，r值越大说明该模型与故障数据之间拟合度越高。相关公式如下：

2.5 可靠度与平均无故障工作时间计算

当确定各个子系统的分布模型后，可按照式(8)计算可靠度的点估计值。典型分布平均无故障工作时间MTBF点估计值计算公式如表4所示。

表4 MTBF点估计值计算表

按照上述步骤，计算得到数控磨床整机及各个子系统可靠性指标如表5所示。

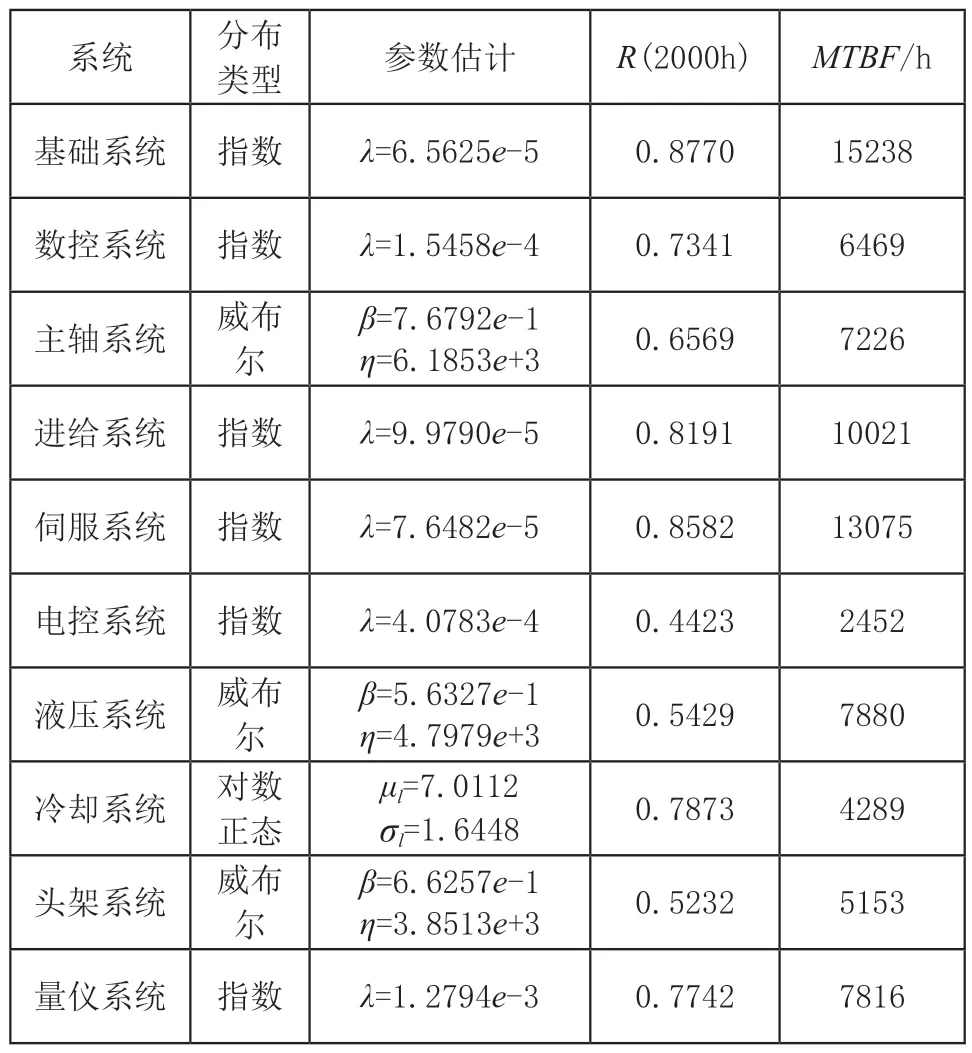
表5 数控磨床子系统可靠性指标表

3 可靠性分配

3.1 可靠性影响因素集

结合表1中数控磨床故障数据及上文相关定义，获得数控磨床子系统可靠性影响因素表如表6所示。

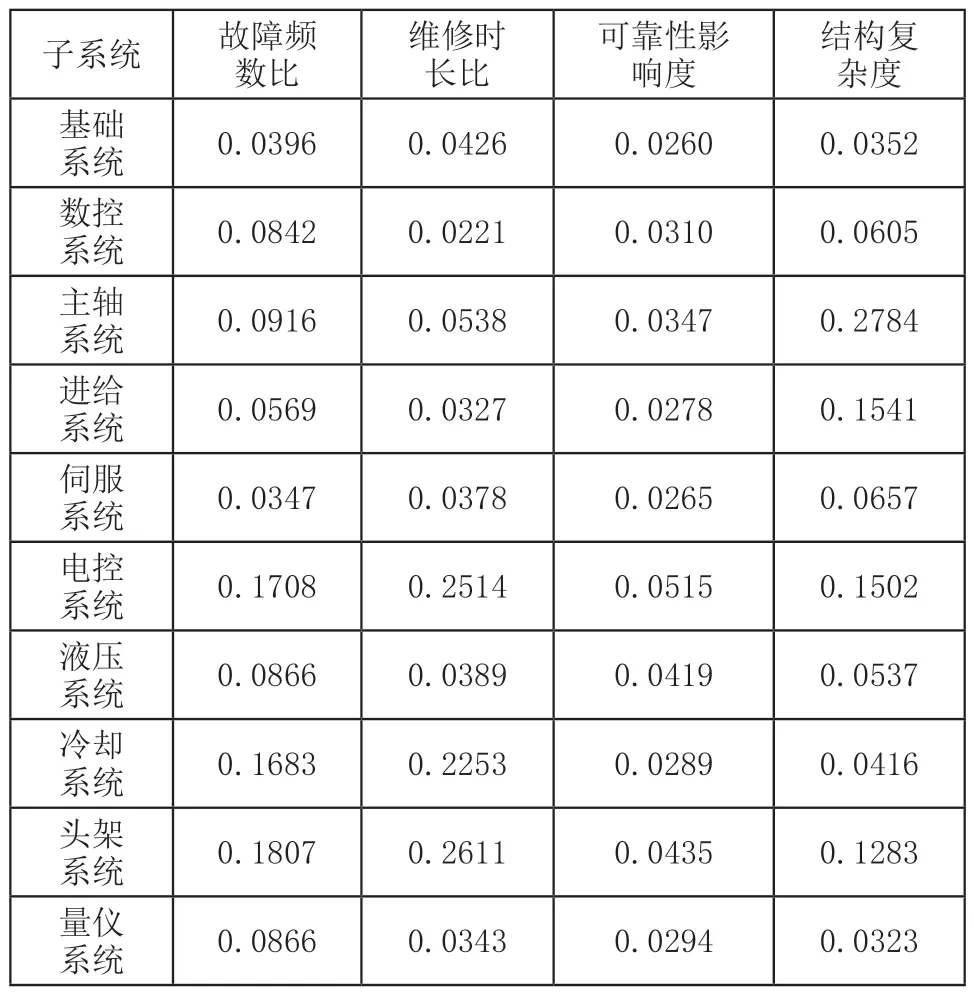
表6 数控磨床子系统可靠性影响因素表

3.2 影响因素隶属度矩阵

以数控磨床各子系统故障频次比k1为例，计算各子系统隶属度向量M1过程如下：

利用式(5)计算得到矩阵uij(k1)为：

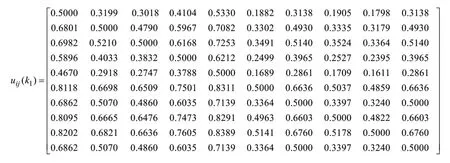
利用式(6)计算得到隶属度向量M1为：

同理可得隶属度向量M2、M3和M4,则数控磨床影响因素隶属度矩阵M为：

3.3 熵权法计算综合影响度

利用式(2)对控磨床影响因素隶属度矩阵M标准化，得到标准化隶属度矩阵MS。

利用式(3)计算得到对应熵值为：

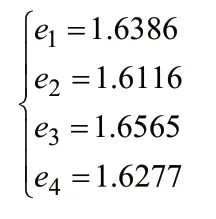
利用式(4)计算得到对应权重为：

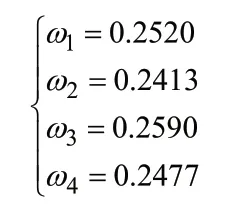
故数控磨床各个子系统可靠度的综合影响度为：

3.4 阿林斯分配

阿林斯是一种考虑重要度的可靠性分配方法，将综合影响度视为重要度，可获得各子系统可靠度R和平均故障间隔时间MTBF的分配值，计算公式如下：

式中，Ci—子系统i的重要度；

λiq—子系统i分配后的故障率值；

λsq—整机设计时的故障率值；

λiq—子系统i分配后的可靠度值；

λsq—整机设计时的可靠度值；

MTBFiq—子系统i分配后平均故障间隔时间；

MTBFsq—整机设计时的平均故障间隔时间；

将设计值Rsq=0.9代入式(12)，计算得到各子系统分配后的可靠度值，将设计值MTBFsq=2000h代入式(13)～式(15)，计算得到各子系统分配后的故障率值和MTBF值，计算结果如表6所示。

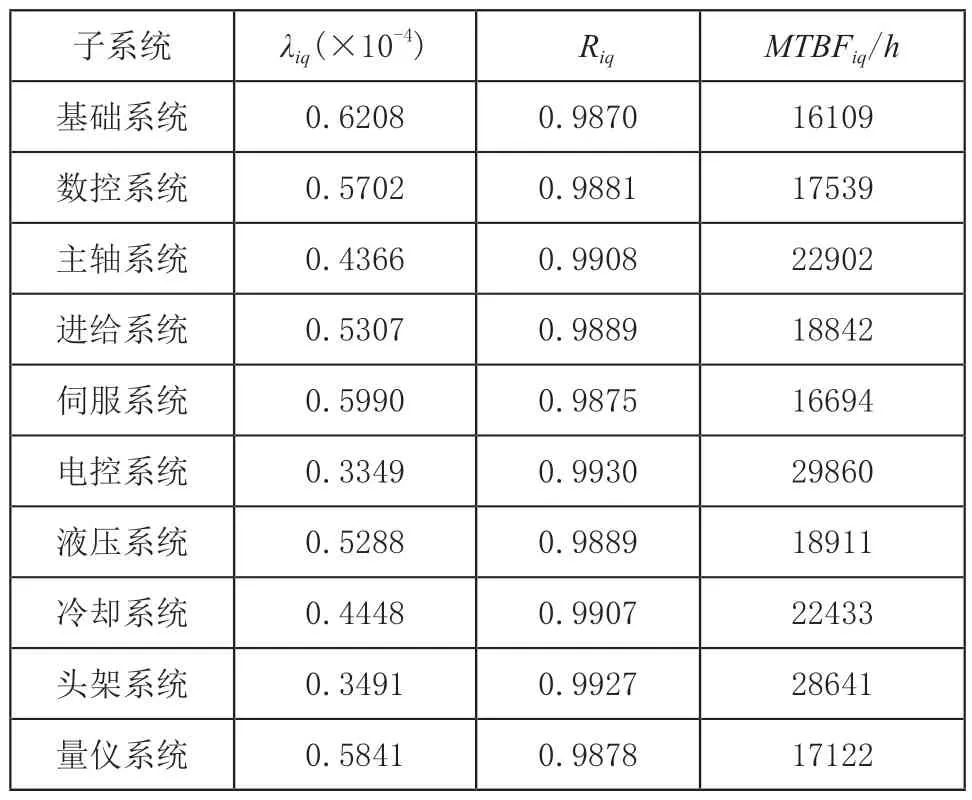
表6 数控磨床子系统分配后可靠性指标表

4 可靠性优化

将整机故障数据按照第2节进行可靠性建模，发现整机故障故障间隔时间分布符合λ=6.053e-4的指数分布，进而可以得到现阶段的可靠度R和平均故障间隔时间MTBF。数控磨床整机及子系统分配前后可靠性指标对比如表7所示。

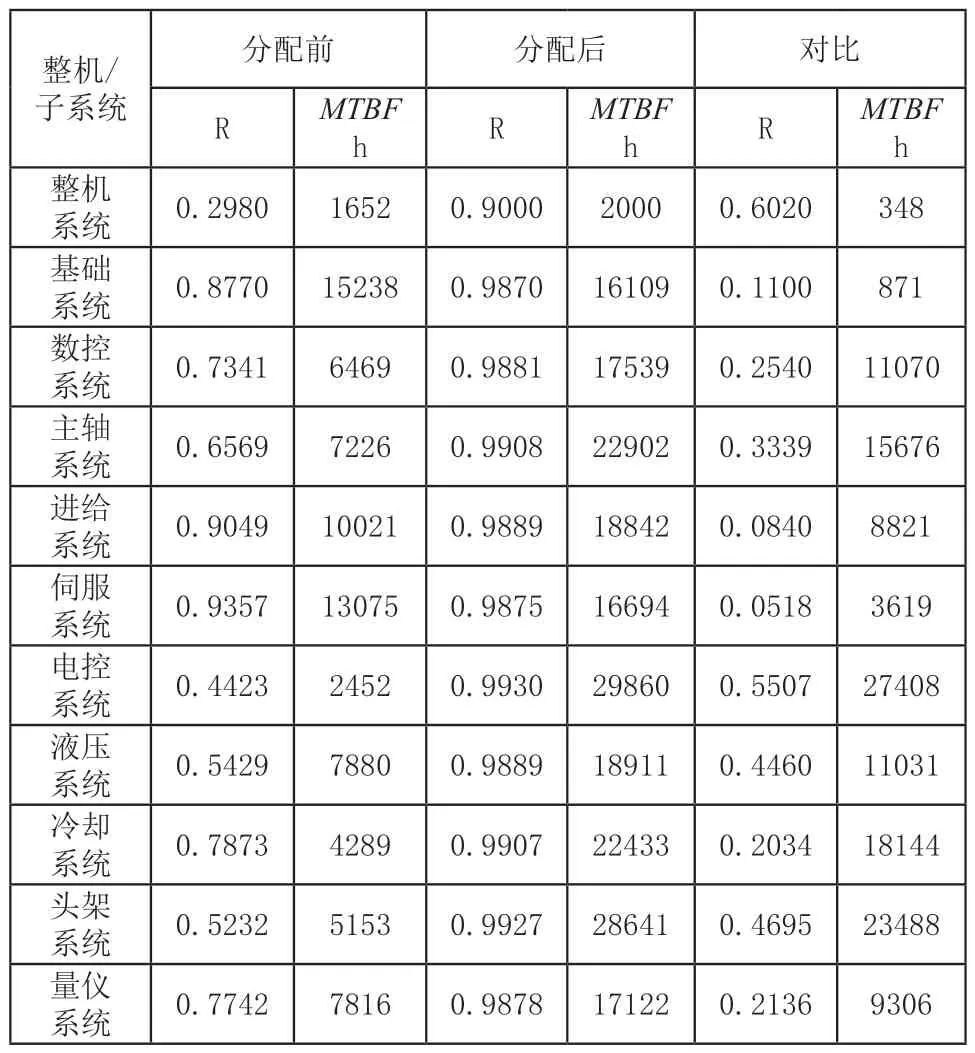
表7 整机及子系统分配前后可靠性指标对比表

从表7中可以看出，每个子系统可靠度R和平均故障间隔时间MTBF均需要提升，为进一步明确子系统可靠性优化顺序，以MTBF对比值为标准，建立优化强度函数P(t)为：

利用优化强度函数P(t)，建立子系统可靠性优化等级模型如表8所示。

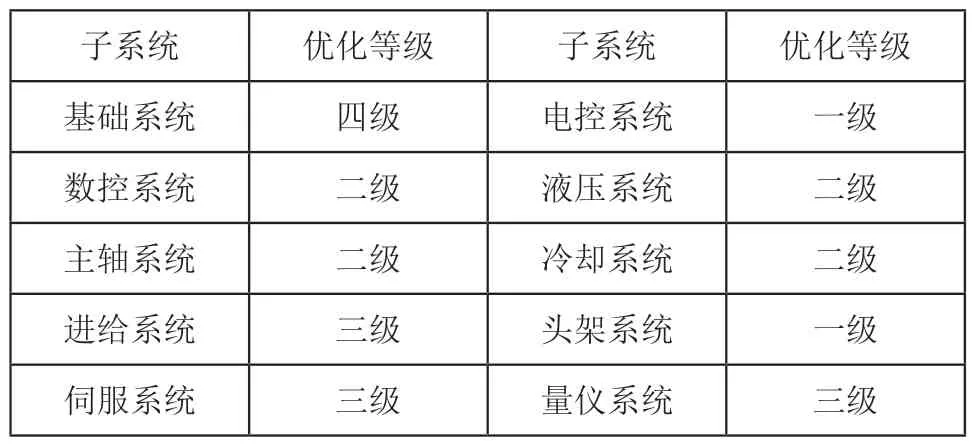
表8 子系统优化顺序表

由表8可以看出，电控系统和头架系统属于可靠性第一优化等级，因其结构复杂，构件众多，因此企业应加强外购零件的品质管理；数控系统、主轴系统、液压系统和冷却系统属于可靠性第二优化等级，因其故障多为人员违规操作导致，因此在加强外购件可靠性的基础上，应加强对员工的日常培训；进给系统、伺服系统和量仪系统属于可靠性第三优化等级，该部分组件多为精密元器件，易受工作环境影响，因此企业应定期对其开展检查、保养和维修工作；基础系统属于可靠性第四优化等级，该部分多为机床本体，因此企业应合理优化其零件布局，增强整体强度。

5 结语

文章在计算数控磨床整机及子系统现有可靠度R和平均故障间隔时间MTBF的基础上，提出了一种基于改进模糊—熵权的可靠性分配优化方法，确定了每个子系统可靠度R和MTBF分配后应该达到的数值，并对其可靠性优化的先后顺序做了排序，并提出了可靠性改良建议。该方法能克服传统方法忽视机械结构和主观性过强的缺点，对数控磨床整机MTBF达到2000h设计值具有重要指导意义。