基于BP神经网络预测的内燃机车转速控制方法
王耀琦,任相,王小鹏
(兰州交通大学 电子与信息工程学院,兰州 730070)
0 引言
在我国初期铁路运输中内燃机车占据主导地位,现阶段由于铁路电气化改造以及动车组列车的发展,内燃机车在铁路运输中起着辅导性作业[1,2]。内燃机车广泛运用于工程车以及环境恶劣的地方的铁路运输,所以在铁路运输中,内燃机车也起着不可忽视地位。柴油机是内燃机车的动力源,柴油机发出功率需要和内燃机车带的负载匹配,所以柴油机在工作时需恒速运行[3]。然而机车在行驶过程中会受到线路阻力变化,使负载发生扰动,导致转速发生波动,柴油机发出的功率与牵引电动机的功率不能匹配,导致机车容易发生卸载现象。目前,普通内燃机车使用PID控制进行调速控制,而PID控制中三个参数是一个针对全局的最优控制,导致动态性能不强鲁棒性差。在机车运行过程中,机车转速控制系统是一个时变的、非线性系统,针对不同工况PID控制的强度也不同,所以采用PID转速控制时,控制性能不佳,鲁棒性差[4]。
内燃机车转速控制的性能与采用的控制方法有很大的关系,好的控制方法能使机车在运行过程中针对负载扰动的情况下,依旧安全平稳的运行。关于内燃机车转速控制已经有许多学者做出研究,针对解决问题的点不同采用不同的解决方法。文献[5]使用PID控制运用在内燃机车转速控制中,由于使用一个全局的最优控制参数,导致鲁棒性差,同时由于内燃机车柴油机模型是一个复杂的系统导致数学模型不够精确,而PID控制对数学模型精度要求高,导致控制性能不佳,响应速度慢、超调量大和稳定时间长。针对PID控制采用一个全局的最优控制参数和对数学模型精度要求高的特点,文献[6]中提出模糊控制应用在内燃机车转速控制中,该文章中采用了二维模糊控制,分析了误差和误差变化率,提高了非线性的内燃机车转速控制系统的控制性能。在工业控制中,PID控制由于其简单性和实用性,使PID控制运用最为广泛,但是PID控制采用一个全局的参数且对非线性系统控制性能不佳,文献[7]中提出模糊自适应PID控制应用在内燃机车转速控制中,同时解决了模糊控制中缺少微分的环节导致不能使误差降为零和PID控制参数不能更改的问题。以上方法对内燃机车转速控制展现了良好的控制性能,但是内燃机车转速控制系统是一个非线性、时变性和时滞性的系统,且难以获得精确的数学模型,导致控制性能和鲁棒性不佳。
综上所述,传统的控制方法对于内燃机车转速控制中难以达到所期望的性能和鲁棒性。模型预测控制(Model Predictive Control,MPC)采用被控对象的动态模型预测系统未来输出,同时结合滚动优化和反馈校正的控制方法[8,9]。与PID控制相比MPC不但拥有反馈校正的特点,同时还根据预测模型预测系统未来的输出,并实施滚动优化,使MPC在非线性、时变性和时滞性的系统中的控制性能优于传统的控制方法。神经网络是一个通用逼近器,能够以任意精度逼近任何系统,在神经网络中BP神经网络结构简单且训练算法成熟[10~12]。结合BP神经网络和MPC的优点,本文提出BP神经网络并运用于内燃机车转速控制系统中。
1 BP神经网络预测控制算法原理
1.1 模型预测控制算法
模型预测控制算法原理主要包括预测模型、滚动优化和反馈校正,框图如图1所示[13]。

图1 MPC算法原理框图
非线性系统的输入输出模型表示为[14,15]:

式(1)中,y(k)表示系统输出向量,f(·)表示非线性未知函数,u(k)表示控制输入向量,na表示为输出阶数,nb表示为输入阶数。
MPC是通过滚动优化实施控制的,所以在每个采样时刻k,需要实时求解非线性优化问题得出控制作用。当在采样时刻k的约束条件为式(2)时:
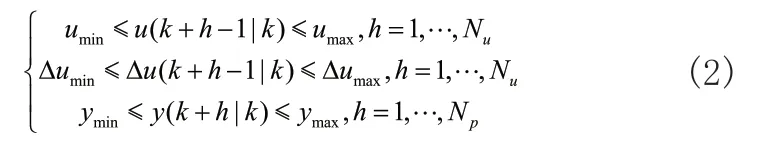
其中,控制增量如公式(3)所示:
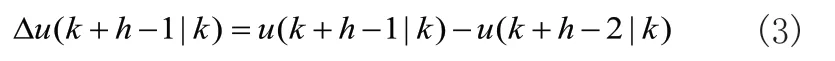
优化性能指标如式(4)所示:

式(4)中,J(k)表示为k时刻优化性能指标,r(k+h丨k)表示为从k时刻开始后的第h步的期望输出,y(k+h丨k)表示为从k时刻开始后的第h步的预测输出,Np表示为预测时域,Nu为控制时域,且Np>Nu>0,qh为控制加权系数,umin和umax表示为k时刻开始后的第h步的期望输出最小值和最大值,Δumin和Δumax表示为控制增量的最小值和最大值,ymin和ymax为k时刻开始后的第h步的预测输出的最小值和最大值。
1.2 BP神经网络算法
神经网络对非线性系统的拟合能力很强,公式(1)所示的非线性系统模型的具体表达式未知,对该模型的输入输出样本数据通过神经网络对其建模[16,17]。在神经网络中,反向传播网即BP(Back Propagation)神经网络结构简单且训练算法成熟,所以本文采用如图2所示的BP神经网络对非线性系统进行建模。
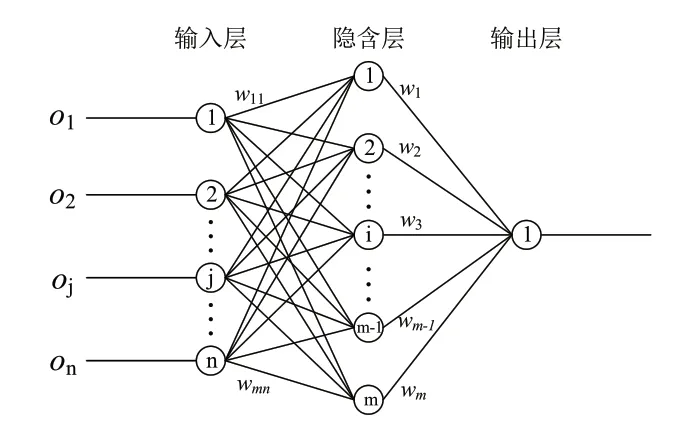
图2 BP神经网络结构
根据BP神经网络工作原理可得,隐含层节点i的输入xi如式(5)所示:

式(5)中,oj为输入层的输出,其中j=1,···,n,wij为输入层节点j到隐含层节点i的连接权重,wi0为隐含层节点i的输入偏差。隐含层节点输出zi如式(6)所示:

式(6)中,φ(·)为神经元激活函数,本文采用的神经元激活函数为sigmoid函数,该函数如图3所示。输出层节点的输出为如式(7)所示:

图3 sigmoid神经元激活函数

式(7)中,w0为输出层节点的输入偏差,wi为隐含层节点i到输出层节点的连接权重。
反向传播原理是BP神经网络的核心,即通过给定的数据样本集更改网络中的连接权重和输入偏差,使性能指标E达到最小值,如式(8)所示:
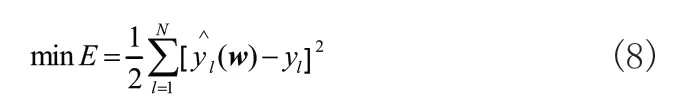
式(8)中,N为样本数,yl为第l组样本中系统输出值,为第l组样本中通过式(7)得出的神经网络输出值,w为连接权重和输入偏差的参数向量。在设定初始参数向量w后,根据梯度法改进网络参数如式(9)所示:

式(9)中,wnew为更新后的参数向量,wold为更新前参数向量,η为学习率。式(9)所示的参数向量一直更新,直到式(8)所示的性能指标达到最小值,这时得到的BP网与样本数据集匹配最佳。
1.3 BP神经网络预测控制算法
对如图1所示的模型预测控制算法进行改进,首先把预测模型改进为BP神经网络建模进行模型预测,然后将滚动优化改进为采用神经网络的在线优化控制器,算法原理框图如图4所示。
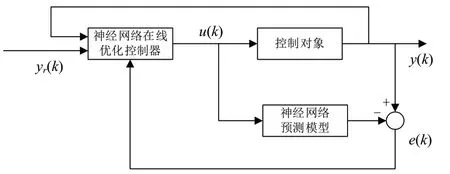
图4 BP神经网络预测控制算法原理框图
根据BP神经网络算法原理,可以对式(1)所示的非线性系统的输入输出模型进行BP神经网络建模,即可以进行模型预测。预测控制是对未来输出实现多步预测,当预测步数为P时,即需要建立P个BP网,根据式(1)、式(5)、式(6)和式(7)可以得出第s个BP网可以表示为:
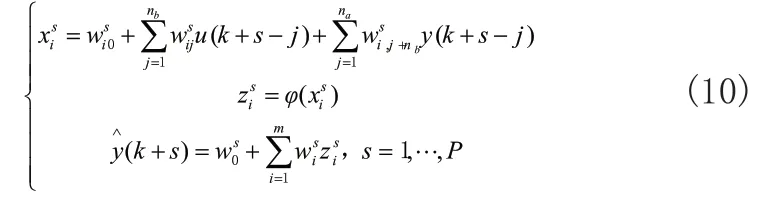
工作原理与单个BP网的工作原理相同,只是输入量在时间上进行相应的移位,使网络的输出反应为未来不同时刻的输出预测值。所以可以对经典的预测控制中的滚动优化采用神经网络在线优化控制器,且优化采取和模型参数辨识相似的梯度寻优过程实现。
k时刻的优化性能指标如式(11)所示:
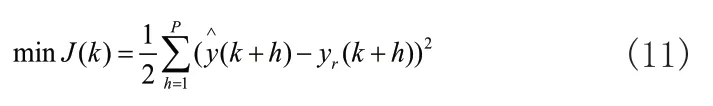
式(11)中,(k+h)是各个BP网在输入为u(k+h-1)时的预测输出,yr(k+h)是输出期望值,其中h=1,...,P,所以:
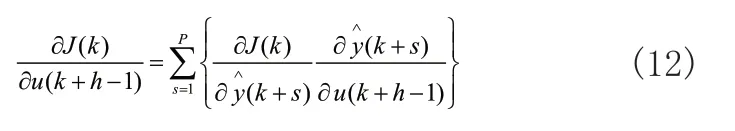
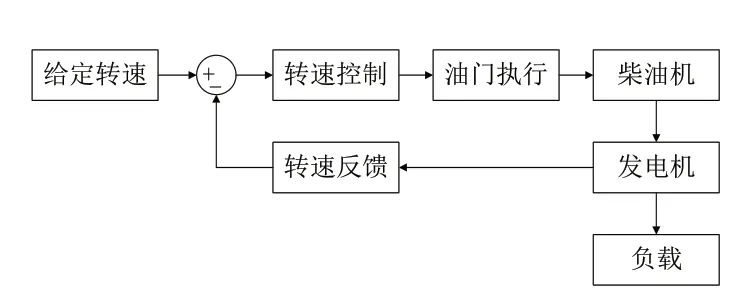
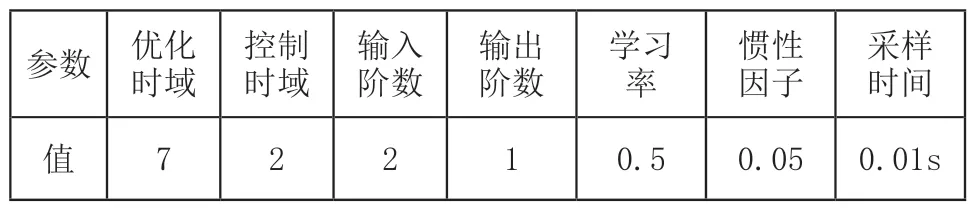
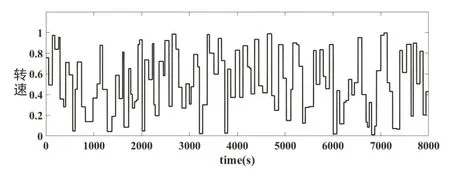
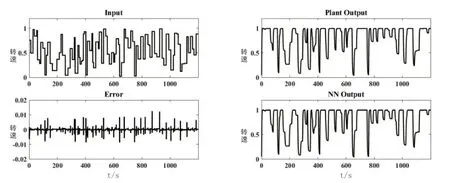
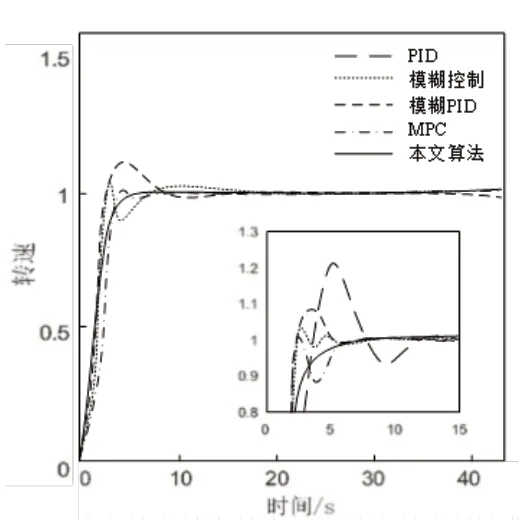
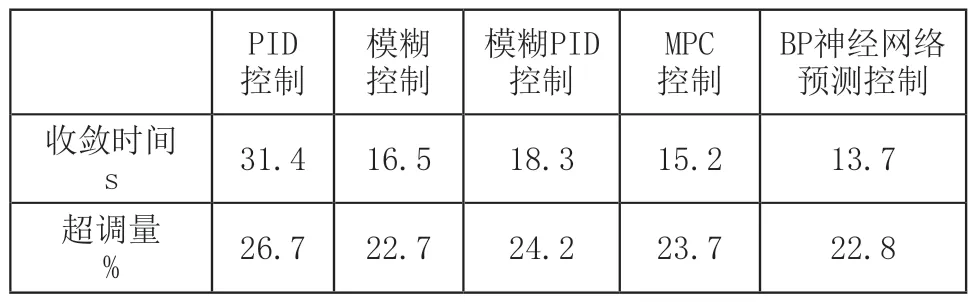
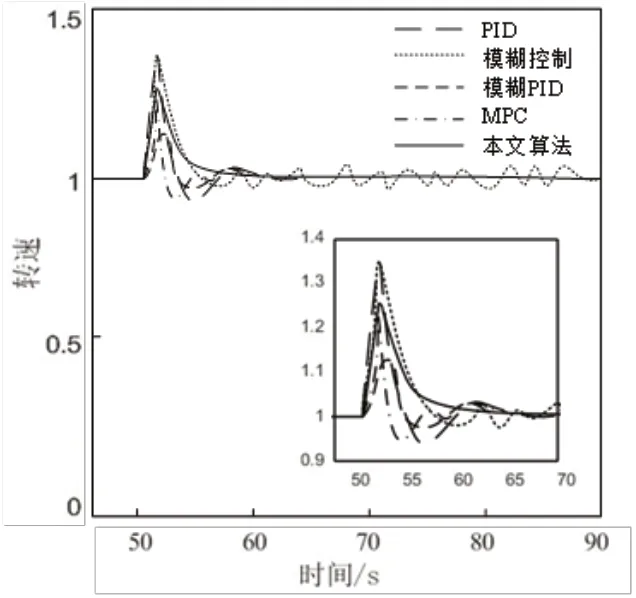
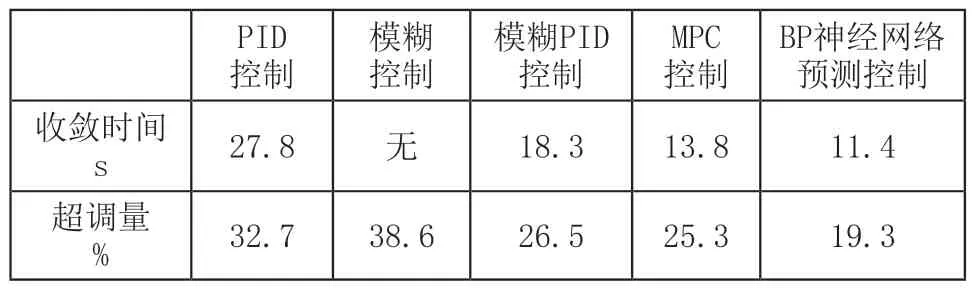
当s 其中, 根据式(11)可以得到: 结合式(12)~式(15)可以得出: 根据理论推导,可以设置一组控制量uM(k),利用如式(10)所示的模型得出y~PM(k),代入式(11)得出J(k)中的根据梯度法对控制量进行改进: 式(17)中,α为步长,根据式(16)计算得出,unew(k+h-1)为更新后的k时刻开始后的第h-1步的控制输出,uold(k+h-1)为更新前的k时刻开始后的第h-1步的控制输出。迭代过程反复进行,直到优化性能指标J(k)达到最小值,这时的u(k)作为最优控制量作用到系统实施控制。 内燃机车转速控模型主要包括给定转速,油门执行,柴油机和发电机模块,控制框图如图5所示。内燃机车转速控制首先将当前发电机的转速通过转速反馈与给定的转速作差值运算,将差值运算结果给转速控制模块,根据转速控制算法得出控制指令,对油门单元进行控制,达到控制柴油机的供油量,使柴油机的转速稳定在给定转速值[18]。 图5 内燃机车转速控制框图 油门执行单元是控制柴油机的供油量,根据转速控制器给的控制信号,控制油门齿条并带动到某一供油位L。所以可以将油门执行单元等效为一阶惯性环节,传递函数如式(18)所示: 式(18)中,Ts为油门执行单元时间常数。 柴油机单元是根据油门执行单元对供油量的控制,从而控制柴油机的输出力矩Tm,达到转速控制的目的。由于柴油机的油料燃烧和热力冲程,致使油门执行单元对柴油机的输出力矩的控制存在时滞性。油门执行单元对齿条位移L和柴油机输出的输出力矩Tm成正比关系如式(19)所示: 式(19)中,k为正比例系数。 根据式(19)可得,当油门齿条位移变化量为ΔL时,柴油机的输出力矩的变化量如式(20)所示: 假设柴油机的滞后时间常数为Td,得出柴油机在复频域的输出力矩的变化量如式(21)所示: 根据泰勒级数可得: 内燃机车转速控制系统中,时间滞后常数Td很小,所以可以把式(22)中分母中的二次项和多项式可以忽略不计,所以柴油机的传递函数如式(23)所示: 转速反馈单元是通过转速传感器对发电机的转速进行采集,并把采集后的转速信号通过信号转换电路转换为一定比例的电压信号t。转速反馈的传递函数如公式(24)所示: 为了验证本文所提算法的有效性,通过MATLAB/Simulink对BP神经网络预测控制的内燃机车转速控制系统建模,为了全方面分析控制的有效性和鲁棒性,与传统PID控制、模糊控制、模糊自适应PID控制和MPC进行对比并分为两种工况进行验证。 在MATLAB/Simulink对内燃机转速控制系统进行建模中,发电机模块采用”Synchronous Machine pu Standard”为标幺值同步发电机,油门执行单元时间常数Ts=1,柴油机滞后时间常数Td=1.5,比例系数k=1,同时在内燃机车转速控制中各个机械环节间存在时间滞后,需加入一个为0.1的延时。神经网络预测模型参数设置如表1所示。 表1 神经网络预测模型参数 在试验前需要对被控对象模型进行训练,将一系列随机阶跃序列作用于被控对象模型生成训练数据,训练样本设置为8000,随机阶跃序列如图6所示,训练数据结果如图7所示。 图6 随机阶跃序列 图7 训练数据结果 生成训练数据后,选择trainlm训练算法开始训练被控对象模型,迭代次数设置为200,验证数据结果如图8所示,训练完成后的被控对象模型响应数据如图9所示。 图8 验证数据图 图9 训练响应数据图 完成神经网络训练后,对基于BP神经网络预测的内燃机车进行转速控制实验。 工况一:内燃机车在启动时转速变化。 经过MATLAB/Simulink建模仿真后,工况一仿真结果如图10所示,其中PID控制内燃机车转速在启动时转速变化如图10长虚线所示,模糊控制内燃机车转速在启动时转速变化如图10点线所示,模糊PID控制内燃机车转速在启动时转速变化如图10短虚线所示,MPC控制内燃机车转速在启动时转速变化如图10点划线所示,基于BP神经网络预测控制内燃机车转速在启动时转速变化如图10实线所示。 图10 内燃机车在启动时转速变化 工况一的对比参数如表2所示。 表2 工况一控制性能对比 工况二:内燃机车在运行中负载发生突变。分为两种情况,一是负载变大,二是负载减少。 工况二中情况一是在50s、51s和52s时负载增加一倍,仿真结果如图11所示,其中PID控制内燃机车转速变化如图11长虚线所示,模糊控制内燃机车转速变化如图11点线所示,模糊PID控制内燃机车转速变化如图11短虚线所示,MPC控制内燃机车转速变化如图11点划线所示,基于BP神经网络预测控制内燃机车转速变化如图11实线所示。 图11 内燃机车在运行中负载增加转速变化 工况二中情况一对比参数如表3所示。 表3 工况二情况一控制性能对比 工况二中情况二是在50s时负载减小一倍,仿真结果如图12所示,其中PID控制内燃机车转速变化如图12长虚线所示,模糊控制内燃机车转速变化如图12点虚线所示,模糊PID控制内燃机车转速变化如图12短虚线所示,MPC控制内燃机车转速变化如图12点划线所示,基于BP神经网络预测控制内燃机车转速变化如图12实线所示。 图12 内燃机车在运行中负载减少转速变化 工况二中情况二对比参数如表4所示。 表4 工况二情况二控制性能对比 通过MATLAB/Simulink仿真实验,在工况一实验中,仿真结果对比参数如表1所示,PID控制超调量大,收敛时间慢,模糊控制优于PID控制,但是模糊控制误差不能降为零,模糊PID控制收敛快,超调量大于模糊控制,MPC控制超调量小于模糊控制且收敛时间小于模糊PID控制,BP神经网络预测控制收敛时间快且超调量小。在工况二实验中,PID控制在负载突变的情况下转速波动大,收敛时间慢,模糊控制相比较于PID控制缺少了积分环节导致控制误差不能降为零,控制性能不佳;基于模糊PID控制的内燃机车转速控制解决了PID控制参数问题和模糊控制缺少积分环节问题,使得控制性能优于PID控制和模糊控制;基于MPC控制的内燃机车转速控制采用了模型预测、滚动优化和反馈校正,使得控制性能优于模糊PID控制;基于BP神经网络预测控制对MPC中的模型预测和反馈校正实现BP神经网络预测模型进行模型预测,同时将滚动优化根据神经网络预测模型和优化算法迭代计算得出最优控制量实现滚动优化,使得控制性能优于MPC控制。 针对电传动内燃机车在负载发生扰动下,转速会发生波动,使牵引发电机功率小于牵引电动机功率,导致机车运行不平稳,提出基于BP神经网络预测控制的内燃机车转速控制,采用神经网络逼近进行模型预测,以及采用梯度下降法设计神经网络在线优化控制器,反复优化求解使优化性能指标最小,同时进行反馈校正对神经网络预测模型失配进行补偿,使控制系统的鲁棒性更强。本文通过MATLAB/Simulink对内燃机车转速控制建模进行仿真实验,证明了基于BP神经网络预测控制的内燃机车转速控制的有效性,相较于PID控制、模糊控制、模糊PID控制和MPC控制控制精度高、响应时间快、稳态误差小和鲁棒性好的优点。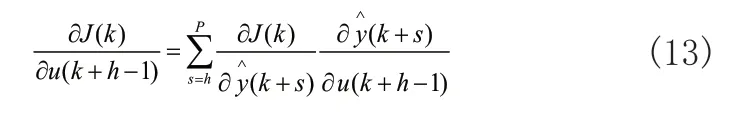
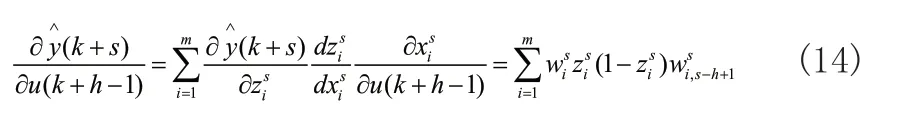
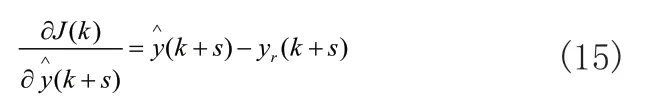
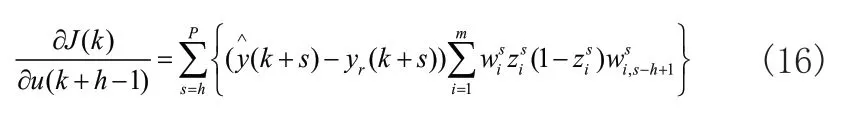
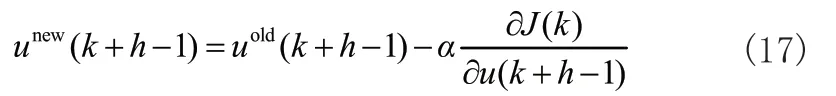
2 内燃机车转速控制数学建模







3 实验验证




4 结语

