尼龙磨耗板多因素生产车间布局优化研究

朱成顺，黄俣钧，李滨城，张辉，吕珏

（1.江苏科技大学 机械工程学院，镇江 212003；2.江苏铁科新材料股份有限公司，镇江 212000）

0 引言

尼龙磨耗板是一种广泛应用于铁路货车行业的小型板类零件。目前该类板材基本采用离散化生产模式和工艺原则的设备布局形式，由工人操作半自动化机床完成加工，手工对工件进行搬运。企业在进行生产规划过程中往往存在如下问题：

1）设备凭经验摆放，使得工位间物流量不平衡，物料搬运时间与机床加工时间不协调，设备利用率较低；

2）因工序分散和任务琐碎，工人作业情况存在明显的动态性和复杂性，采用简化的数学模型难以对车间整体生产过程进行准确有效分析。由此，研究一种以提高生产效率和降低物流运输量为目标，综合考虑工人作业情况的布局优化方法具有重要的理论意义和工程应用价值。

布局优化问题是指基于生产过程中的物流情况，在给定空间内对相关设备资源进行合理布置，使得布局成本最小[1]。Finke等人[2]实验表明该问题是NP-hard问题，随着设备数量和目标函数的增加，求解难度呈指数增长[3]。文献[4]指出设施布局问题应包括人、机、料、物流路线在内的多个生产要素。随着模型和算法的优化与发展以及各类复杂车间问题的出现，许多学者对于车间布局问题展开了多领域集成建模优化研究。徐修立等[5]具体考虑了单元间距和横竖放置问题对车间进行了精准建模；杜吉旺等[6]采用可视图算法对车间布局中的避障路径规划问题进行了分析；邓鸿剑等[7]采用Delmia DPM，Plant Simulation等仿真软件建立车间三维模型，模拟实际生产，针对布局空间的合理性与通畅性问题进行了详细直观的分析和优化。

基于上述研究，针对尼龙承磨板生产车间布局优化的综合问题，本文提出一种以加工时间和物流运输量最小为目标的多要素生产车间布局模型，在模型中综合考虑了工人站立点、行走路径、工作方式等实际因素，结合遗传算法与生产过程仿真对模型进行优化。最后通过Plant Simulation仿真软件及内置算法库对某尼龙板材生产车间进行布局优化，验证了本文方法的有效性。

1 多行多因素布局模型

多行多因素布局模型满足如下基本要求和假设：

1）忽略工作单位细节形状，一律用矩形代替；

2）各工位依据线性布局形式，从车间左上角依次向右布置，工位间根据具体情况留有适当距离，超出车间宽度时自动换行；

3）每个工位内基于不同功能划分为设备区、工作区、上料区和下料区四个区域，工人在各区域内工作点完成相应工作；

4）工人以各工作点作为行走路线的出发点和目的地；

5）车间内设置有用于存放成品的成品区，成品区不与其它工位干涉。

基于上述要求和假设，多行多因素布局模型如图1所示，车间左上角为坐标原点，水平方向与x轴平行，竖直方向与y轴平行；各工位由数字依次标注；L和W分别为车间的水平长度和竖直宽度，I和w分别为各工位的水平长度和竖直宽度；d为各工位间的水平距离，h1和h2分别为各行间的竖直距离，每行的竖直宽度为在此行中的工位最大竖直宽度；xn和yn分别为第n个工位中心点的横坐标与纵坐标。各工位内区域划分如图1中工位3、工位9和工位n所示，其中三个小矩形区域从左至右依次为上料区、工作区和下料区，各区域内工作点位置根据具体情况而定，剩余大矩形区域为设备区，用于摆放机床。车间中间行设置有墙体O，用于铺设电路。各工位机床需靠墙摆放，便于供电及工人出入。成品区设置于车间角落。

图1 多行多因素布局模型

本文采用可视图法和Dijkstra算法[8]形成起点、障碍物顶点、终点之间的最短连线段，用以表示工人搬运工件时避开障碍物的行走路线，则工位间的物流运输距离即为该线段的长度，如图1中虚线S1和S2所示。

工人行走距离计算公式如下：

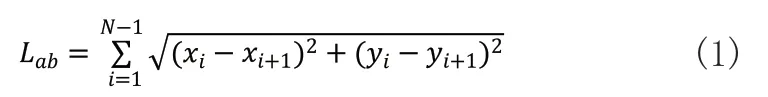
式(1)中Lab为工人从工作点a到工作点b的行走距离，N为工人经过的起点、障碍物顶点、终点的数量之和，xi，yi为工人当前所在点的坐标，xi+1，yi+1为工人基于上述算法确定的下一个目标点的坐标。

多行多因素布局模型约束条件如下：

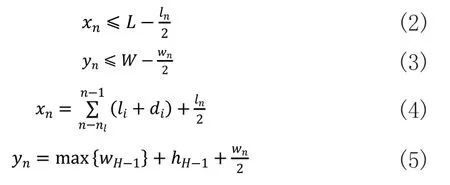
式(2)、式(3)表示工位布局不能超过车间的总长和总宽，式(4)、式(5)为工位横纵坐标计算公式。式(2)中xn为第n个工位的横坐标，L为车间总长，ln为第n个工位的水平长度；式(3)中yn为第n个工位的纵坐标，W为车间总宽，wn为第n个工位的纵向宽度；式(4)中，nl为换行前工位数量，nj为第j个工位的水平长度，di为第i与i+1个工位间的水平间距；式(5)中，H为当前工位所在行，max{H-1}为第H-1行的工位最大纵向宽度，hH-1为第H-1行与第H行的间距。

2 工人作业流程及目标函数

已知磨耗板加工车间配备n台设备和z个工人，其中，某生产周期内有s个工件等待加工。为方便问题研究，对加工过程中工人的作业流程做出如下假设：

1）每台设备作业时间分为装夹时间t1和加工时间t2，其中装夹时间t1内人员与设备协同工作，加工时间t2内设备单独工作；

2）工件的工艺流程已定，且每道工序与设备一一对应；

3）同一设备与人员在某一时刻只能加工一个工件的某一道工序；

4）同一人员可在不同时刻操作多台设备；

5）操作过程及设备加工过程不可中断；

6）当上料区工件不足或下料区工件达到一定数值，工人对工件成批搬运；

7）最后一道工序的工人每次将一批加工完成的工件搬运至成品区，代表车间成功出料一次。

基于上述假设，工人作业流程如图2所示。

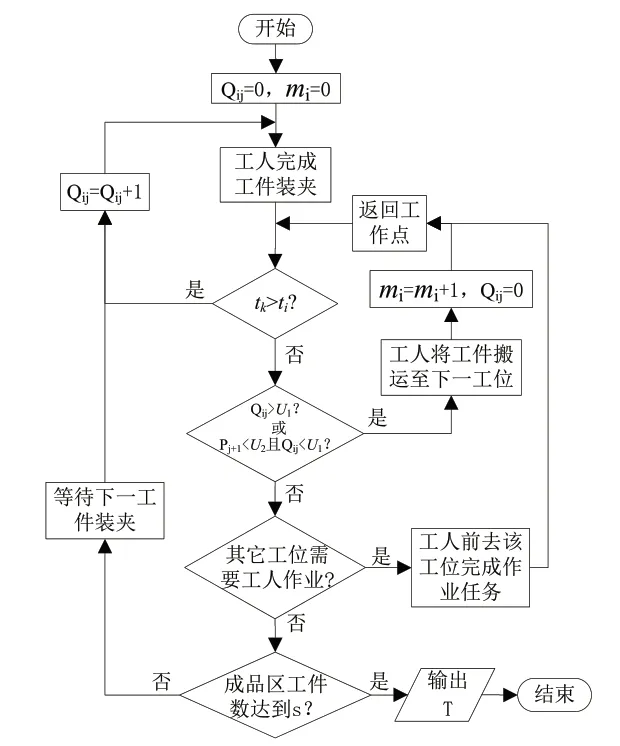
图2 工人作业流程

（1）出料次数mi及每批次工件数Qij初始值为0，前一工位工件抵达工位i上料区，该工位上的工人k在工作点进行工件装夹；

（2）工人结束装夹时间ti1，进入加工时间ti2后处于空闲状态，在该段时间内工人可执行如下a,b,c,d四项工作：

a如无其他指令，工人原地待命，监测机床运行状况；

b当该工位下料区的工件数Qij达到U1件时，工人到达下料点，花费时间将所有工件搬至推车上，并运输至下一工位的上料点，再花费时间将工件从推车搬至下一工位的上料区(若该工位为最后一道工序，则工人直接将工件搬运至成品区),搬运完成后原路返回工作点，等待加工时间ti2结束或直接进入下一次装夹时间ti1；

c当下一工位上料区的工件数Pi+1不足U2件，且该工位下料区工件数Qij未达到U1件时，工人重复事件b中的操作；

d当其他工位需要调用该工人进行装夹或搬运时，工人花费时间tka完成作业后返回工作点，等待加工时间ti2结束或直接进入下次装夹时间ti1。

上述事件的优先级为b>c>d>a。

（3）当成品区工件数达到s件时，输出完工时间T。

优化模型目标函数如下：

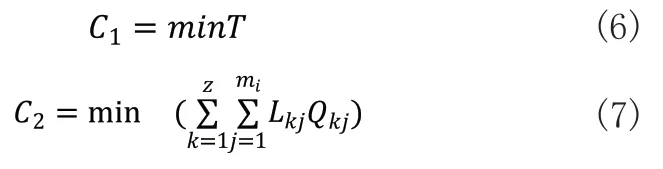
式(6)、式(7)为目标函数，式(6)表示总完工时间最小，用于反应生成效率的提升，式(7)表示总物流运输量最小。式(6)中T为加工s个工件的完工时间，由生产过程仿真获得，式(7)Lab中为第k个工人搬运第j批次工件的行走距离。Qkj为该批次工件数量，mi为该工位总搬运批次数。

参考文献[5]，采用加权法构造新的优化目标函数，将多目标优化问题转换为单目标优化问题进行求解，考虑到车间可能存在多种工件的加工，且每种工件的市场需求不同，对每种工件完工时间分开计算，并取不同的权值：

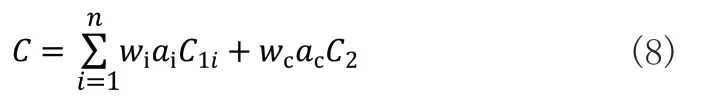
式(8)中ai、ac为归一化因子，wi为每种工件完工时间的加权因子，wc为车间总物流量的加权因子，满足

工人作业流程的约束条件如下：

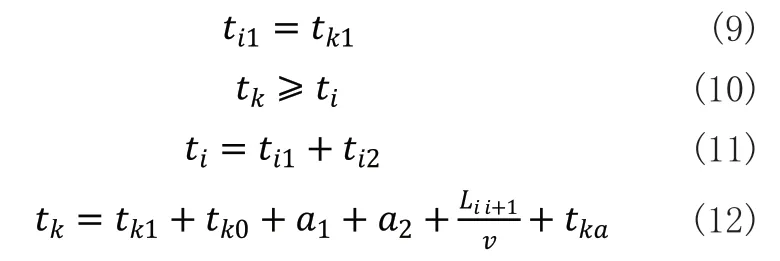
式(9)表示装夹时间内工人与机床必须协同工作，式(10)表示工件的实际完工时间不小于理论完工时间，式(11)、式(12)分别为工人理论完工时间与实际完工时间的计算方法，式(12)中tk为工位i到i+1的物料运输时间，v为工人平均行走速度，根据实际情况获得。

3 集成生产过程仿真的遗传算法优化过程

针对上述车间布局优化问题，首先基于染色体编码形成多行布局模型，通过生产过程仿真获得目标函数，并采用遗传算法对目标函数进行优化求解，具体流程如图3所示。

图3 结合生产过程仿真的遗传算法流程

1）编码设计

本文采用单行序列结合自动换行策略对多行设备进行编码，以每个工位作为基因，则染色体(1,2,3,…,n)表示图1中初始的布局顺序，超出车间长度时将进行换行。每个染色体表示一种布局顺序，一代种群包含了若干个染色体。

2）适应度函数

参考文献[9]，将目标函数式(8)的最小值问题转化为式(13)的最大值问题，以便后文应用优化算法计算适应度值，式中T为一个极小的正数，用于避免分母为零的状况出现。

3）遗传算子及终止条件

选择操作采用轮盘赌的方式，交叉操作采用顺序交叉，交叉发生概率取0.8，变异操作采用逆转变异，变异发生概率取0.1，终止条件为遗传算法进化到设定的世代数后自动停止。

4 案例分析

某尼龙承磨板制造企业主要生产旁承磨耗板P1和支承磨耗板P2两种小型尼龙板材，零件示意图如图4所示。

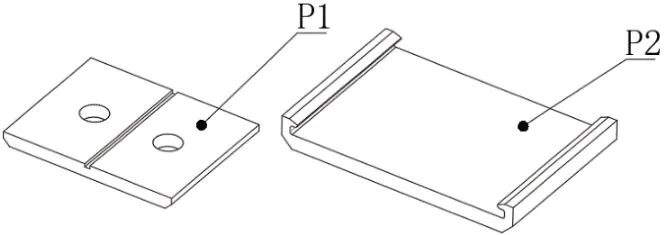
图4 加工零件示意图

已知生产工件P1共需8道工序，设置有11台机床和9个工人，生产工件P2共需6道工序，设置有10台机床和6个工人，零件P1日产量1200件，零件P2日产量600件，其工艺流程及初始布局如图5所示。数字标注的为支承座P2加工工位，字母标注的为尼龙承磨板P1的加工工位，一个数字或字母代表一个拥有该项技能的工人，数字或字母相同的多个工位由同一个工人完成加工，毛坯从车间左上角运入，各道工序从第一行车加工开始。各工位共占据6行，已知第3、4两行间铺设有电器设备，第2～5行左侧设置有防护栏，图中用黑色粗线表示，工人无法从此处穿越，整个车间被分为上下两个区域。第1、2和5、6两行之间以及防护栏左侧设置有工人通道，因此工人从车间上半区域向下半区域运料只能走左侧工人通道。

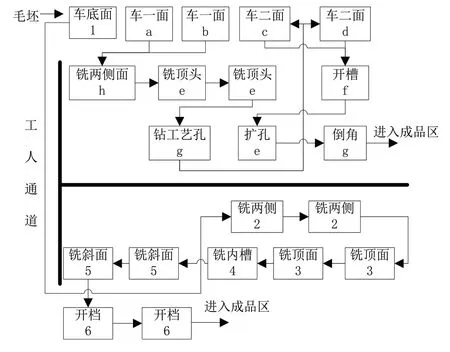
图5 原始工艺流程及设备布局

经现场调研，该车间长20m，宽19m，第一行各工位横向间无工人通过，最小间距为1m，从第二行开始各工位横向间均有工人通过，最小间距为1.2m，工人通道宽1.7m，障碍物宽0.55m，车间内存在较多闲置区域，下料区最大存储量及工人一次搬运量均为120件，上料区最小存储量为15件，工人行走的平均速度约为1.2m/s，上下料时间均为5s，各工位尺寸及作业时间如表1所示。

表1 工位尺寸及作业时间

5 优化结果

采用上文相关参数，运用Plantsimulation仿真软件及内置Simtalk编程语言建立布局模型和工人作业流程。以该车间两种工件的日产量为终止条件计算目标函数，对模型中21个工位按顺序编码，采用Plantsimulation内置遗传算法库对布局进行优化，考虑毛坯从车间左上角运入且从车加工开始，优化过程中限制车加工工位编码只能布置于第一行。设置种群规模为20，迭代次数为200，取加权因子1进行实验，优化后的布局模型如图6所示，图中红色矩形框为工件P1加工工位，蓝色矩形框为工件P2加工工位，橙色细线为工人的行走轨迹。获得优化结果如表2所示。

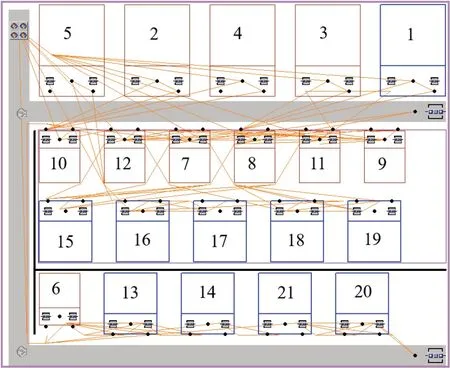
图6 基于Plant Simulation的仿真布局模型

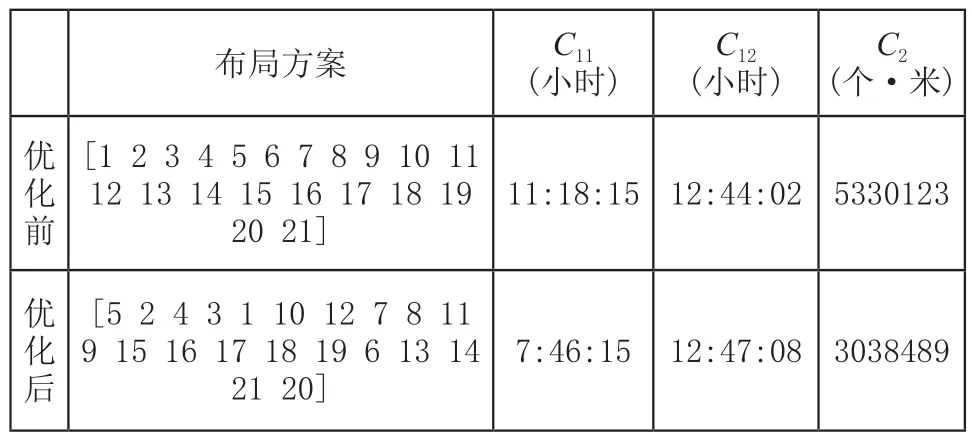
表2 优化结果

对比表2中数据可知，优化后工件P1的完工时间及车间总物流运输量相较初始布局均获得较大减少，验证了本文优化方法的有效性；而工件P2的完工时间难以降低，说明初始布局下P2完工时间已基本达到最优，需考虑其他方法进一步优化。

6 结语

本文针对尼龙承磨板加工车间生产效率不足、物流频繁的问题，通过生产过程仿真与遗传算法相结合的方式，实现完工时间和物流运输量的同步优化。并在仿真过程中综合考虑人员作业位置、作业流程和避障路径，用以获取更详细的生产过程参数。最后通过某企业案例，证明了本文优化方法的有效性。但布局调整的优化效果有限，下一步将考虑工人调度与布局的集成优化，实现生产效率的进一步提升。