基于田口方法与灰色关联分析的碰撞射流通风系统优化
齐贺闯, 叶 筱, 亢燕铭, 钟 珂
(1.上海工程技术大学 机械与汽车工程学院, 上海 201620;2.东华大学 环境科学与工程学院, 上海 201620)
“碳达峰”“碳中和”已列为中国未来几十年的重要发展战略。据统计,通风、空调能耗占建筑总能耗的50%以上[1]。为加速实现“碳中和”目标,如何使建筑通风、空调系统更绿色高效已成为暖通空调行业无法回避的现实考题。
合理的气流组织是营造良好室内热环境、改善室内空气品质和提高通风效率的关键[2]。Gao等[3]研究指出,因送风设计参数如送风速度和温度、送风口形状等对室内气流组织具有耦合影响,在进行空调系统设计时,合理匹配设计参数之间的关系是需要考虑的主要因素之一。此外,理想空调系统预期达到的目标是在兼顾节能的同时维持良好室内热舒适和空气品质,但是,这些评价指标对系统整体通风性能的优化存在相互制约关系,比如,维持良好室内热舒适所对应的设计变量组合可能导致较差的室内空气品质,或虽实现了节能目标,但不能提供良好的室内热舒适[4-5]。因此,将上述通风性能评价指标同时考虑在内是进行通风、空调系统优化设计的另一关键因素。
碰撞射流通风(impinging jet ventilation,IJV)是近几年逐渐发展起来的一种新型通风策略,可同时实现节能、提供良好室内热舒适和空气品质的目标,且兼顾供冷和供暖功能[6-8]。虽然大量研究针对IJV的通风性能展开,但这些研究均将衡量IJV通风性能优劣的指标(如室内热舒适、空气品质及节能特性等)单独进行分析[6-10],很少有文献对这些评价指标同时进行优化研究。此外,关于设计变量与通风性能之间匹配关系的研究大多借助单因素试验方法,因素间交互作用对整体通风性能的影响尚不明确。因此,如何合理匹配设计参数间的组合关系使IJV整体通风性能达到最优,成为目前应重点关注的问题。
以一个典型双人办公室为研究对象,提出一种基于田口方法和灰色关联分析相结合的IJV多目标同时优化方法,解决IJV的多目标、多设计参数同时优化问题。首先,以送风口高度、送风速度和送风温差为研究变量(即设计变量),以室内热舒适(如头足温差Δt和吹风感Dr)、空气质量(如呼吸区空气龄τbz)和系统节能特性(如送风能量利用系数η)为目标变量,利用田口试验方法研究上述设计变量对各目标变量影响的显著性。在此基础上,借助统计学理论中的灰色关联分析法将多目标同时优化问题转化为单目标优化,并给出IJV整体通风性能达到最优时的设计变量匹配关系。最后,通过试验对所获得的最佳组合条件进行合理性验证。研究结果不仅可为IJV的优化设计提供理论指导,而且可为暖通空调领域多目标同时优化问题提供新思路。
1 试验设计与数值计算模型
1.1 田口方法的试验设计
田口方法(Taguchi method)[11]以误差因素模拟各种干扰,运用信噪比RS/N作为稳健性指标(即质量评价指标),从而寻求最优试验设计方案。文献[6]指出,影响IJV通风性能的主要设计参量包括送风速度、送风温差、送风口高度、回风口高度等。考虑到目前办公建筑大多采用回风口和排风口共用的回/排风方式,本文仅选取送风口高度h、送风速度vs和送风温差Δts共3个因素作为研究变量。选取头足温差Δt、吹风感Dr作为室内热舒适性的评价指标,呼吸区(取距离地面1.1 m高度的区域)空气龄τbz作为室内空气质量的评价指标,送风能量利用系数η作为节能特性的评价指标[12]。
根据田口试验方法,将上述3个研究变量分别设定在高(3)、中(2)、低(1)3个水平。采用田口试验中的L9(33)正交表制定试验方案,如表1所示。
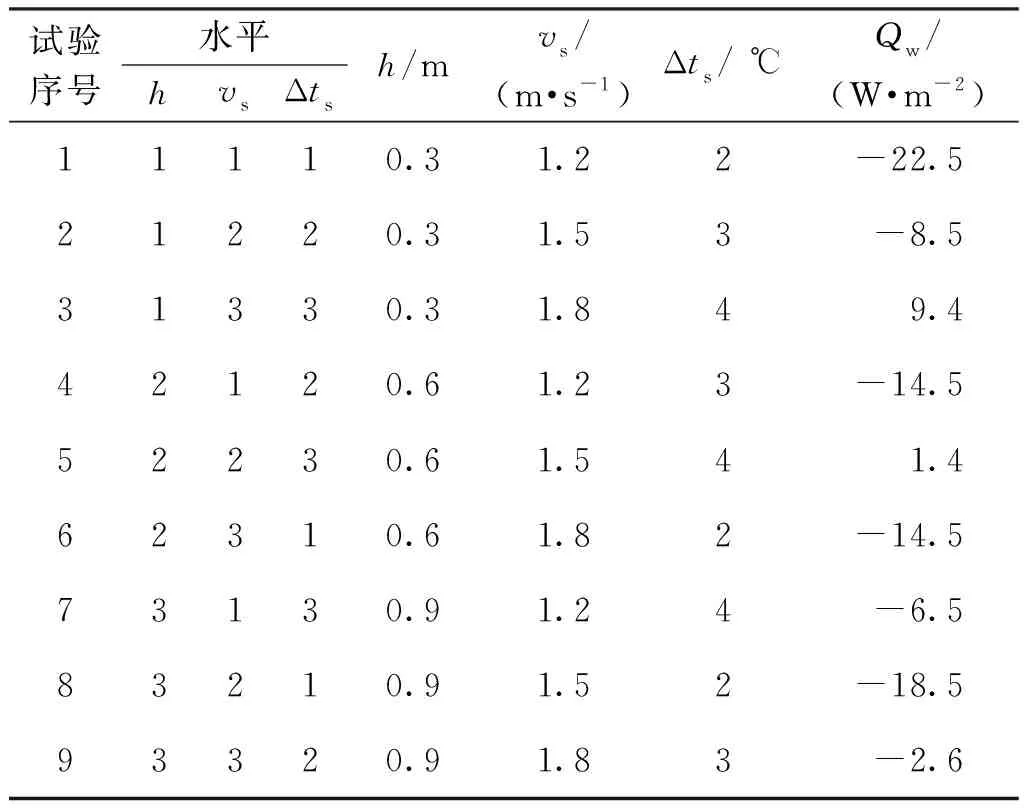
表1 田口试验L9(33)正交表Table 1 Taguchi’s L9(33) orthogonal array
1.2 计算流体动力学数值模拟
1.2.1 物理模型及边界条件
以一个房间尺寸长为3.6 m(x)、宽为4.2 m(y)、高为2.7 m(z)的双人办公室为研究对象,该房间的3 D透视图如图1所示。IJV的送风管道为半圆形,紧贴北墙布置,送风口直径为0.4 m,距离地面的高度为h。回风口布置在屋顶中央,尺寸为0.3 m×0.2 m。另外,在外墙侧设有一扇尺寸为4.2 m×1.2 m的窗户(见图1),窗墙面积比为0.44。

图1 物理模型Fig.1 Physical model
室内包括两个简化的人体模型(均处于坐姿状态)、两台电脑、一张桌子和两盏吊灯,如图1所示,其中,每个人体模型的散热量为80 W,每盏吊灯的散热量为36 W,每台电脑的散热量为100 W。由此可知,由内部热源所引起的室内总冷负荷为432 W。模拟过程中认为,与所研究房间相邻的房间均为空调房间,除外墙为热损失面外,其他墙面(包括屋顶和地面)均设为绝热面。外墙的边界条件按第二类边界条件处理,设为恒定热流密度。对于表1所列不同工况,通过调整外墙的热损失强度Qw使工作区(取为1.3 m以下空间)平均温度维持在热舒适状态,即(25.0±0.3)℃。各个工况所对应的外墙热损失强度Qw列于表1中。
1.2.2 数值计算方法
设室内空气流动为三维连续、不可压缩流,采用Reynolds时均N-S方程计算室内空气的湍流流动,湍流模型选用RNGκ-ε两方程模型。数值计算时,考虑到浮力的影响,空气密度采用Boussinesq假设[13],采用SIMPLE算法对压力和速度项进行求解。关于模型的离散化,除压力项采用标准Standard格式外,其他项均选用二阶迎风格式。所有固体表面均设为无渗透和无滑移条件,送风口边界类型设为velocity-inlet,并假定流速均匀,排风口边界定义为outflow。
采用非结构化四面体网格划分物理模型,并且对室内温度和速度变化较快的热源表面、送风口、回风口及近壁面等区域的网格进行加密处理。本研究中的最小网格尺寸为0.05 m,网格增长因子为1.15,最终所划分的网格总数为311万。
1.2.3 数学模型的合理性验证
为验证数值计算方法的合理性,采用与文献[14]相同的边界条件和室内热源条件,对采用置换通风房间内的流场和温度场进行数值模拟,并与文献[14]给出的实测结果和模拟值进行对比。房间内共布置了9个测杆,测杆位置如图2所示,具体试验细节详见文献[14]。由于篇幅限制,仅给出3号和9号测杆温度和速度的实测值和模拟值对比,如图3所示。
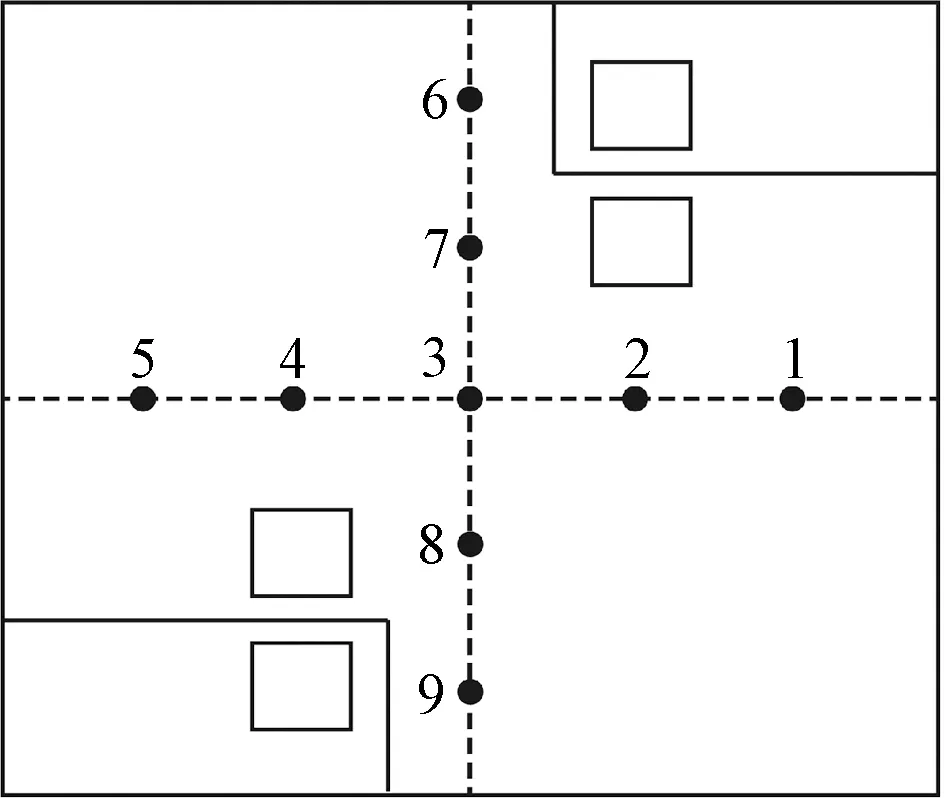
图2 测杆位置Fig.2 Locations of the nine measuring poles

图3 温度和速度的实测值与模拟值对比Fig.3 Comparison of the temperature and velocity distributions between the numerical results and experimental data
由图3可知,本文的数值模拟结果和文献[14]给出的数值结果均与实测值有一定的偏差。对于温度分布,该偏差主要在近地面区域。对于速度分布,这一偏差主要集中在房间下部和顶部区域。造成这一现象的原因归结如下:一方面,由于送风气流被直接送至房间下部,导致近地面区域湍流强度波动明显,而该区域的温度和速度受湍流模型和离散格式的影响较大,从而带来一定的计算偏差;另一方面,由于靠近地板和屋顶区域的气流速度较小,热线风速仪在测量低速度时存在一定的测量误差。总体而言,温度和速度的偏差均处于可接受范围,并且对于多数测点,本文获得的模拟结果与文献[14]的模拟结果均与实测值能够较好地吻合,由此可见本文的数值计算方法是合理可靠的。
2 结果与分析
2.1 田口分析法进行单目标优化
田口方法使用信噪比RS/N作为分析反应的特性值,以达到改善并寻求最优的设计目标。RS/N=平均数/变异数,其大小能够同时反映每次试验的平均值和偏差。信噪比分为望小特性、望目特性和望大特性,其中,望大特性希望质量特性值越大越好,望小特性则希望质量特性值越小越好。本文希望Δt、τbz和Dr越小越好,因此选用望小特性信噪比;希望η越大越好,故选用望大特性信噪比。望大特性和望小特性信噪比的计算公式[11]如式(1)和(2)所示。
望小特性:
(1)
望大特性:
(2)
式中:yi是第i组试验所对应的试验结果;n为试验总次数,本研究中n=9。
利用上述数值模拟方法,对表1所列试验工况的Δt、τbz、Dr和η等进行计算。利用Minitab 17.0软件对处理后的数据进行主效应分析,通过对各项指标进行响应优化,得到各指标所对应的信噪比RS/N。表2给出了各指标的计算结果及所对应的信噪比RS/N。

表2 数值模拟结果及对应的信噪比Table 2 Numerical results and the corresponding signal-to-noise ratio
将各设计变量在不同水平下的信噪比计算平均值,可以得到设计变量对各指标的影响程度,并绘出设计变量信噪比平均值随不同水平的变化图。针对各项评价指标,设计变量在不同水平下的信噪比平均值变化趋势如图4所示。
在效应图中,信噪比随设计变量变化的斜率越大,则该变量对响应值的影响越显著。由图4可以看出:影响头足温差Δt的主效应因素为送风温差Δts> 送风速度vs> 送风口高度h;而对于τbz、Dr和η,影响最大的设计变量均是送风速度vs,其他因素的影响均较小,且相差不大。
信噪比越大则表示一个系统的稳健性越好,代表该因素中此水平处理效果最佳。由图4可知:对于Δt,最佳的设计变量组合条件为h2vs3Δts1;对于τbz,最佳的设计变量组合条件为h2vs3Δts2;对于Dr,最佳的设计变量组合条件为h1vs1Δts1;对于η,最佳的设计变量组合条件为h1vs1Δts2。
由以上分析可知,对于单个评价指标而言,产生最大信噪比所对应的因素水平条件为最优,但对于多个评价目标,某条件下某一指标产生较高信噪比的同时,可能对其他评价指标产生较低的信噪比。比如,送风温差Δts对Δt的信噪比最大,但其对η的信噪比最小(见图4)。
另外,对于不同的评价指标,所得到的最佳设计变量组合也是不同的。显然,分开使用这些评价指标来衡量通风性能的优劣是不准确的,需要对这些指标进行综合评估。田口方法仅适用于对单一目标的优化[11],对于多个目标的优化需要借助其他手段。因此,将借助灰色关联分析法实现多目标参数的优化。
2.2 灰色关联分析的多目标优化
2.2.1 灰色关联分析
灰色关联分析通过计算目标变量的无量纲化数据序列和系统特征变量(灰色关联系数)数据序列的灰色关联度,将复杂的多目标优化问题转化为仅对灰色关联度的单目标优化[15]。在该方法中,首先,利用式(3)和(4)对原始目标变量进行无量纲化处理,结果见表3。然后,通过式(5)计算关联系数。需要指出的是,在进行灰色关联度计算之前,需要评估这4个指标之间的重要层级,即各指标的权重。本文采用熵度量法[16]对各目标变量的权重进行计算,结果发现,Δt、τbz、Dr及η所对应的权重分别为25.32%、24.86%、24.95%和24.87%,四者相差不大。因此,在计算灰色关联度时忽略了权重对关联度计算结果的影响[16]。最后利用式(5)对各目标变量的关联度进行计算。表4给出了各评价指标的灰色关联系数和关联度的计算结果。
望大特性:
(3)
望小特性:
(4)
(5)
(6)

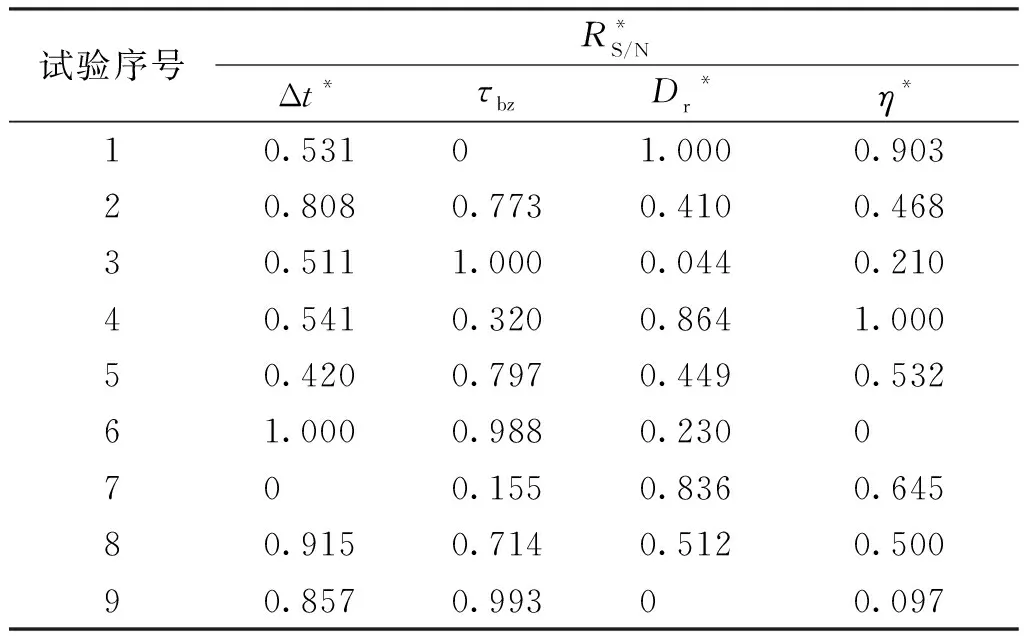
表3 各目标变量信噪比的标准化结果
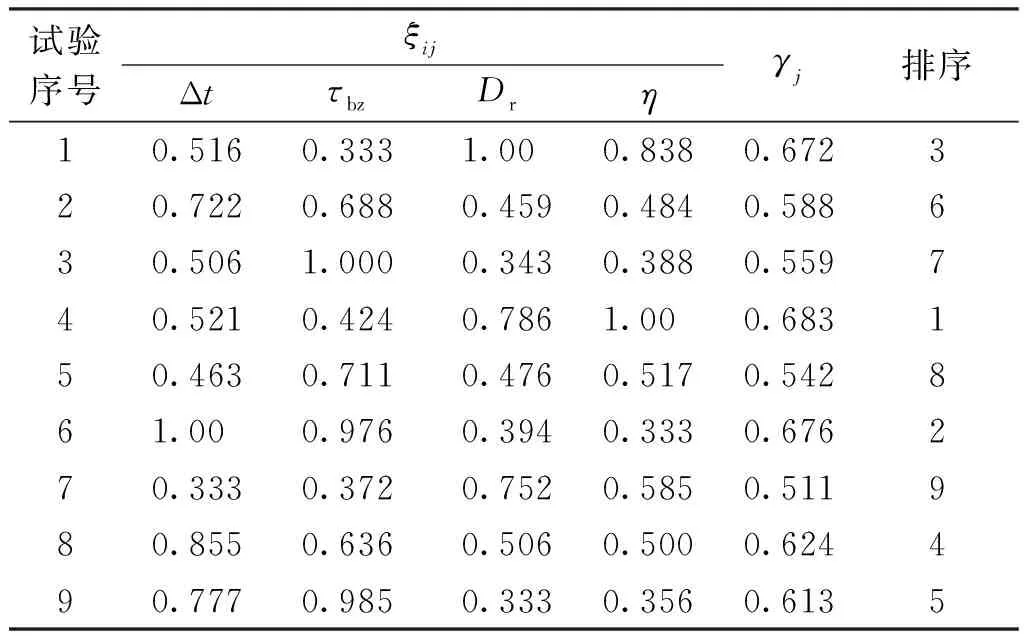
表4 各目标变量的灰色关联系数及灰色关联度
灰色关联度数值越大,表明本组试验值越接近理想值。由表4可知,第4个试验的灰色关联度最大,具有最好的综合性能,其次为第6组和第1组试验。各设计变量在不同水平下的灰色关联度平均值的变化趋势如图5所示。

图5 灰色关联度平均值的变化趋势Fig.5 Variation trend of the averaged gray relational grade
根据图5可知,各因素对IJV整体通风性能的影响程度为Δts>h>vs。为了使灰色关联度最大,h的2号水平、vs的1号水平、ts的1号水平为各因素的最佳水平。
2.2.2 方差分析
方差分析用于确定各设计变量对整体通风性能影响的显著性。表5给出了灰色关联度的方差分析结果。
F值是各因素影响显著性的重要指标,F值越大,说明该因素的影响越显著。由表5可知,对IJV的整体通风性能而言,Δts的影响最显著,h和vs的影响小。从各影响因素的贡献率可知,这3个影响因素都不可忽略。因此,可初步确定h=0.6 m,vs=1.2 m/s,Δts=2 ℃为最佳的设计变量组合。

表5 灰色关联度的方差分析(置信水平:95%)Table 5 Analysis of variance of grey correlation degree (confidence level: 95%)
3 验证试验
由于所得到的最优设计变量组合(h2vs1Δts1)是正交表中没有的方案,故需要做试验予以验证。原始试验方案(h2vs1Δts2)与优化试验方案所得到的试验结果如表6所示。

表6 验证试验结果Table 6 Verify experimental results
由表6可知,优化试验方案后,Δt和Dr均降低,η得到提高,虽然τbz增大了,但增大百分比非常小,可忽略不计。此外,在最优试验方案下预测的灰色关联度γ′j可由式(7)计算得出。
(7)

对验证试验的结果进行分析可知,验证试验的灰色关联度为0.710,与利用式(7)预测的灰色关联度γ′j非常接近,其相对误差仅为3%,结果较为满意。更重要的是,验证试验所得到的灰色关联度比原有试验中最大的灰色关联度(0.683)还要高,这说明通过对信噪比的灰色关联度进行分析,获得了使通风性能更优的设计变量组合h2vs1Δts1。同时也说明灰色关联分析法可用于空调送风系统通风性能的多目标优化,以获得实现最佳通风效果所对应的设计变量组合条件。
4 结 语
利用田口方法的正交试验设计和信噪比理论研究送风温差、送风口高度、送风速度对IJV通风性能的影响,并利用灰色关联分析法将复杂的多目标优化问题转化为仅对灰色关联度单一目标进行优化,得出以下主要结论:
(1)送风温差对头足温差的影响最大,其次为送风速度和送风口高度,而在影响呼吸区空气龄、吹风感和送风能量利用系数的各设计变量中,最大影响因素均是送风速度,其他因素的影响均较小,且相差不大。
(2)对于头足温差,最佳的设计变量组合条件为h2vs3Δts1;对于呼吸区空气龄,最佳的设计变量组合条件为h2vs3Δts2;对于吹风感,最佳的设计变量组合条件为h1vs1Δts1;对于送风能量利用系数,最佳的设计变量组合条件为h1vs1Δts2。
(3)IJV整体通风性能达到最佳的设计变量组合条件为送风速度1.2 m/s、送风温差2 ℃、送风口高度0.6 m。
研究结果对IJV的优化设计具有很强的指导作用,并且基于田口方法的灰色关联分析法可为暖通空调领域所涉及的多目标优化问题提供新思路。

