一种适用于非稳态浅海信道的强化学习自适应调制方案

邱逸凡,张小康,陈东升,童 峰

(1.厦门大学水声通信与海洋信息技术教育部重点实验室，福建厦门361005；2.厦门大学海洋与地球学院，福建厦门361102；3.厦门大学深圳研究院，广东深圳518000)

有限带宽和长传播时延使得水声信道呈现比陆上无线信道复杂得多的传输特性.而由于浅海域存在强烈的海面和海底反射，以及各类人为噪声的影响，浅海信道相较于深海信道表现出更为强烈的时、空、频变参特性，对浅海信道水声通信提出了更高的要求[1].

自适应调制技术是提高通信系统信道适应性的有效手段，相对于在同一调制方式下调整调制参数的自适应调制方法，采用多调制方式的自适应调制可在浅海信道这类恶劣信道下提供更大的适应范围.Benson等[2]提出了一种基于时延扩展和多普勒扩展以及信噪比条件来选择相干调制和非相干调制的自适应调制系统；Mani等[3]在此基础上提出了用可实现的信息速率和均衡后的信噪比作为评判标准的可变速率自适应调制编码技术，并通过实验验证其可行性；Radosevic等[4]和Wan等[5]提出了利用自适应比特和功率分配来实现正交频分复用(orthogonal frequency division multiplexing,OFDM)自适应调制的算法，并提出了新的评判通信性能的指标.邱逸凡等[6]提出了一种利用信噪比、多径、多普勒作为信道状态信息，多种通信制式切换的自适应调制方案，利用该信息，能够有效全面地反映信道条件，仿真结果证明相较于单一制式，该方案能有效提升通信性能.

虽然上述方案相较于单一制式有不少性能的提升，但是在水声信道条件下，这些传统基于阈值判断和反馈的自适应调制方式因时延较长而存在反馈过时的问题，往往导致反馈信息无法反映当前信道状态，从而造成性能下降.近些年，随着人工智能研究的火热开展，机器学习被广泛应用于各个领域[7-8].作为其中分支之一的强化学习，因其在与环境交互过程中通过在线试错获取数据，并自主学习实现模型优化的特点，十分适用于数据量有限、动态变化的水声环境.已有不少相关的文献将强化学习应用于诸如路由协议[9]、水下物联网的网络中继和能量控制[10]、水下机器人(AUV)和节点定位[11]以及自适应通信[12-14]等方向中.强化学习能够通过不断试错和探索学习信道变化，故根据反馈的奖励和状态值能够实现对下一状态的预测，从而有效解决反馈过时的问题.

Song等[12]提出了一种基于Dyna-Q的自适应调制算法，利用有效信噪比衡量信道状态，通过Dyna-Q算法预测下一状态和通信吞吐量，并在移动AUV场景下进行了效果验证；苏为等[13]提出了一种基于强化学习的自适应调制编码方案，该方案在无需知道信道模型的先验知识下可以根据信道质量服务的需求，来选择传输策略，以提高通信效率；李萍等[14]提出了一种基于Sarsa算法的自适应调制方法，仿真结果表明该方法可以保证系统可靠性的同时提高通信吞吐量.总体而言，将强化学习应用于水声通信自适应调制的相关研究还比较有限，且目前的研究大都是基于同一通信制式进行调制参数的优化调整，对于具有复杂时-空-频变参特性的浅海水声信道而言，具有多个不同通信制式的自适应调制方案可提供更为突出的调整能力.此外，Abdallah等[15]中提出针对嘈杂的非稳态环境，Q学习(QL)算法和Dyna-Q算法都存在一定程度的性能下降，而浅海信道正是一个变化频繁且复杂的环境，这可能导致学习过程中，原有环境已经发生变化.

针对以上情况，本文设计了一种基于重复更新Q学习(RUQL)算法的浅海信道自适应调制方案，该算法解决了QL存在的策略偏离的问题[15]，同时保持了简单性.实验设立5种水声通信调制制式，通过试错和探索来学习出每一状态下的最优调制选择，从而在无需预先知道信道模型的情况下实现自适应以提升通信吞吐量，并利用海试数据进行的自适应调制性分析验证本文方案的有效性.

1 浅海信道模型

描述声波在海洋中的传播有3类常用的模型：射线声学模型、简正波模型和抛物线方程近似模型[16].简正波模型通常用于描述500 Hz以下的声传播，而抛物线方程在计算复杂度上比射线模型大得多.因此描述高频水声通信模型常基于射线声学进行信道建模.水声信道冲激响应可以用式(1)描述：

(1)

其中，Ap(t)表示幅度响应，τp(t)是时变信道的时间延迟，δ为狄拉克函数.

浅海信道中，由于海面和海底界面的存在，声波传播可以看成柱面扩展，其传播损失可用下式表示[17]：

10lgA(l,f)=NF+10lgl+

lα(f,S,T,c,pH,z)，

(2)

其中：l是发射机和接收机的距离(m)；f是频率(kHz)；参数NF是一个归一化因子，与发射功率的倒数有关；α(f,S,T,c, pH,z)是衰减系数(dB/m)，与环境参数频率f(kHz)、盐度S(ppt)、温度T(℃)、声速c(m/s)、酸碱度pH和深度z(m)有关.

水声信道中的噪声可以分为环境噪声和外部干扰噪声，环境噪声包含扰动、舰船、风成和热噪声等.这些噪声源组合在统计学上可以近似看成是非白高斯噪声.而浅海区域中，生物、人工机械噪声频发，这也使通信环境变得更加恶劣.针对此类信道，能够根据环境选择最优调制方式的通信体制显得十分必要.

2 基于RUQL的自适应调制

强化学习作为机器学习的分支之一，是一种通过观察智能体与环境交互过程中得到的奖赏来学习对应的策略，以实现长期回报最大化的方法.通常用于解决决策、资源分配等问题.马尔可夫模型作为强化学习中的基本模型，可以用来描述水声通信的过程.一个马尔可夫过程包含动作集、状态集、状态转移概率和回报函数四要素[18].由于水声信道的时-空-频随机变化的特点，状态转移概率难以得知，因而采用强化学习思想中的时序差分学习，该思想结合了蒙特卡洛方法和动态规划两种思想的特点，既可以直接从与环境交互的经验中学习策略，亦可基于目前已得到的其他状态的估计值来更新当前状态的价值函数.其中，QL和Sarsa两种经典算法被广泛应用.

Sarsa算法与QL算法都是基于Q表来学习最优策略，不同之处在于Sarsa算法进行Q表更新时，当前状态下选择的动作，和下一个状态选择的动作都是已知的.即QL在选择下一个动作时，是遵循maxQ的结果，其行为和行为值函数更新选择的是不同的策略.而Sarsa算法在选择下一个动作时遵循贪婪策略，计算Q表时也是用贪婪策略选择的动作计算得来.因此，Sarsa算法相较于QL算法更加保守.Sarsa算法更新公式如下所示：

Q(St，At)←Q(St，At)+α[Rt+1+

γQ(St+1，At+1)-Q(St，At)]，

(3)

式中，Q为动作价值函数，S为状态集合，A为动作集合，R为奖励值，α为当前经验的权重，γ为折扣系数，t为当前时刻.

与Sarsa算法不同，QL更新动作价值函数无需知道下一刻的动作，直接根据下一时刻Q表的最大值进行更新，与生成数据的策略无关，故是一种离轨策略.其更新公式如下：

Q(St，At)←Q(St，At)+α[Rt+1+

γmaxQ(St+1，At+1)-Q(St，At)]，

(4)

Sarsa和QL算法都是基于无模型的强化学习算法，而Dyna-Q则是将基于模型和无模型的强化学习相结合.它既在模型中学习，也在交互中学习.即在每个迭代过程中，先和环境交互并更新价值函数、策略函数，接着进行n次模型的模拟预测，同样更新价值函数、策略函数.这样同时利用了与环境交互的经验以及模型的预测，相比传统QL能够加速学习过程.

在静止的马尔科夫环境中，QL算法可以得出最优策略.然而，由于水声信道的复杂性，实际环境并不总是静止的.而在非平稳环境中，QL算法会存在策略偏差问题[15].策略偏差问题指的是，在传统QL算法的学习过程中，那些具有暂时性低值的最优行动被执行的频率较低，因此，这些行动的值被更新的频率较低.这会造成一个现象，即当代理人学习最佳行动之前，环境可能已经发生了变化，从而导致性能下降.

RUQL的基本思想是调整传统QL算法中的学习率，使得较少选择的动作具有较高的学习速率.如果以低概率π(s,a)选择一个动作，那么不是更新相应的动作值Q(s,a)一次，而是重复更新1/π(s,a)次.更新表达式与QL的更新表达式式(4)一致.

在本文中，考虑使用贪婪算法，即

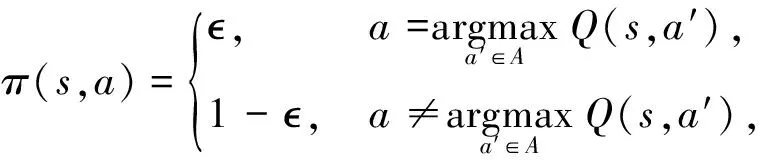
(5)

其中:π(s,a)为在状态s下选择动作a的概率;是一个小常数，表示探索率,越高，代理人会更积极地探索行动空间.

本文将表征水声信道条件的输出信噪比和多普勒频偏作为状态集合，而将采用的调制方式作为动作集合，用通信速率和误码率的综合评估作为奖励值，输出信噪比的定义如下所示.

(6)

其中，Psignal是信号功率，Pnoise是噪声功率.

传统自适应调制方案根据仿真来获得信道质量与调制制式之间的关系，并把它以查表的形式储存在通信机中.但实际上由于信道不完全服从理想的分布，加性噪声也不全是高斯的，导致了固定的切换阈值很难满足误码率的要求.而基于强化学习的自适应调制编码算法则可以克服这个问题，它不依赖于完美的数学模型，能够根据系统的实际误码率性能来确定信道状态和通信制式之间的对应关系.

3 自适应调制方案

传统的自适应调制方案采用阈值判断的方法，通过将信道状态划分为多个区间，将接收端获得的信道状态信息反馈到发射端，然后根据预先设定的区间选择下一个调制方式.但由于时延的影响，这种方法存在反馈过时的问题，导致当前的状态信息并不能很好地反映当前实际信道，造成通信性能的下降.因此将强化学习与自适应调制相结合，在与信道的交互过程中不断更新状态-动作值函数，并利用该函数学习出动态信道下的最佳自适应调制策略，在保证误码率的同时，提高吞吐量性能.

所谓自适应调制，则是能够根据信道状态自适应选择满足误码率前提下的最优调制编码体制，在信道条件差时选择稳健的调制方式以保证误码率，而在信道条件好时选择高速的调制方式以提升吞吐量.因此，误码率和通信速率是自适应调制方案综合考虑的两个指标.给出系统吞吐量的定义[12]，当误码率大于0.1时，此时通信视为失败，成功传输的比特数已无意义，故此时吞吐量记为0，表达式如下：

(7)

其中：RBE为实际误码率；Vt为通信速率,单位为bit/s.

自适应调制的目标是实现Φ的长期最大化，因此将Φ映射到强化学习中，则可将每次选择调制方式后获得的奖励与误码率和通信速率联系起来.目前水声通信中常用的通信制式主要分为非相干调制、单载波调制、多载波调制三类.其中多进制频移键控(Multiple-ary frequency shift keying，MFSK)、多进制相移键控(multiple-ary phase shift keying，MPSK)和OFDM分别为3类中的典型制式，而直接扩频序列(direct sequence spread spectrum，DSSS)因其鲁棒性强也被广泛应用.考虑到海洋环境的复杂性，以及不同应用场景对水声数据传输需求的多样性，不同通信体制能提供的水声信道适应能力比不同调制参数要强，因此本文从不同制式出发，制定出不同制式切换的方案.同时根据实验室现有换能器带宽条件，在各自能够达到的最大速率基础上制定了每种制式的通信速率，以表现各种制式在相应场景下的工作特点，设置5种制式：差分正交PSK(DQPSK)、差分二进制PSK(DBPSK)、OFDM、8进制FSK(8FSK)、DSSS.

自适应调制方案的目标为：保证误码率的同时，最大化系统吞吐量.因此，可以将奖励与每一次成功传输的比特数联系起来，本文设计的奖励函数R如下：

R=

(8)

其中:Vti为第i个制式的通信速率；P为反馈链路出错的概率，这里假设存在某些时刻由于环境影响，导致接收端获得的奖励值并不能正确反馈给发射端，从而影响下一次的Q表更新;Pfail为0～1的随机概率.

由于本文采用的每种通信制式的通信速率大小不同，使得在误码率0.1以下时，即使高速率制式误码率比低速率制式更高，但是吞吐量上仍然会大于低速率制式.因此，误码率在0.1以下时，将不再考虑误码率对通信性能的影响，只考虑通信速率，同时速率越高，奖励值越高.系统在接收端解调后，得到信道状态信息和奖励值，并将这些值返回到发射端，发射端根据奖励值和当前状态更新Q表，并采用贪婪算法选择下一个调制方式.每一个轮次代表一次完整的状态变化过程，从初始状态到终止状态.经历多轮迭代过程后，算法收敛.基于RUQL的自适应调制算法，具体步骤如下.

1) 初始化Q(s，a),∀St∈S,At∈A;

2) 重复经历一个软次：

初始化状态St；

3) 重复一轮中的每一步

用Q表计算策略π,

根据策略π选取一个调制方式At,

执行调制方式At,观察奖励值r和下一个状态s′,

循环1/π(s,a)次：

更新Q表

Q(St，At)←Q(St，At)+α[Rt+1+

结束

s←s′,

直至终止状态,返回2);

4) 获得最终策略.

在经过多次迭代之后，智能体即发射端可以获得策略，即调制制式的选择准则.当信道状态变化时，则发射端能够根据反馈信息和策略，选择使长期吞吐量最大化的制式，从而达到性能的稳定提升.

4 实验结果及分析

4.1 实验设置

实验数据采集地点为厦门五缘湾海域，海域水深8 m，收发机距离为608 m，布放深度为5 m.发射时，信号经声卡、功放、变压器由发射换能器发出；接收时，先由换能器接收信号，再经过前置放大和带通滤波后得到最终的接收信号.换能器带宽为13～18 kHz，采样频率96 kHz，信号带宽4.8 kHz，中心频率15.5 kHz.录制信号共包含DQPSK、OFDM、DPBSK、8FSK、DSSS 5种制式，对应通信速率分别为2 381，2 044，1 172，155，55 bit/s.取每种制式录制数据中的一帧作为原始接收数据，进行实录噪声、多普勒叠加以模拟信道时变.

在接收端，5种通信制式均采用经典方法接收机结构，如表1所示[19-21].所取5种制式原始接收数据的RSN在15～23 dB之间，图1为5种通信制式原始接收数据对应的信道响应，可看出信道存在较为明显的多径结构，多径扩展均在3 ms左右.

图1 被测信道的冲激响应Fig.1Impulse response of the tested channel

表1 5种调制方式接收机结构

4.2 数据处理

在得到每种制式的原始接收数据和实录环境噪声后，为了体现通信过程信道变化，在原始接收数据上根据设置的RSN进行实录噪声叠加和多普勒频偏添加，采用时域重采样对整个输入信号进行多普勒的叠加.为了便于Q表的建立，将RSN和多普勒频偏进行离散化处理.RSN和多普勒频偏分别设置为0～15 dB和0～8 Hz.

定义fDP为多普勒频偏值(Hz)，因此可以将RSN和多普勒频偏组成一个二元组(RSN,fDP),作为状态的表征.为了体现信道的动态变化，将设置两种信道变化过程，每隔一段时间D后，采用另一种变化过程，以此构造一个非稳态环境.第一种变化过程:设置初始状态(15，0)，随后的每一个状态按照RSN减小1 dB、多普勒不变，例如(14，0)，(13，0)……，直至RSN减为0 dB；下一状态RSN变为15 dB，多普勒频偏增加 1 Hz，即(15，1)，重复上述操作；如此反复，直至终止状态(0,8)，从初始状态到终止状态共有144种状态.第二种变化过程：设置初试状态为(15，8), 随后的每一个状态按照RSN减小1 dB、多普勒不变，例如(14，8)，(13，8)……，直至RSN减为0 dB；下一个状态RSN变为15 dB，多普勒减小1 Hz，即(15，7)；如此反复，直至终止状态(0,0)，同样一共有144种状态.

由上述过程可知，在每次RUQL算法的迭代过程中，一共会经历144种信道状态，在每个状态下，RUQL选择一种调制方式，发射一次数据包，因此共有144个数据通信包.强化学习中设置参数α=0.1，γ=0.1；为了更快收敛，将贪婪算法中的设置为0.1，D设置为10，即每10次迭代后环境发生一次变化.P=0.1，即奖励值反馈链路出错的概率为0.1.

同样地，对文献[12, 14]提出的Dyna-Q算法和Sarsa算法以及传统QL算法进行上述的迭代训练过程，作为对比实验.

最后，为进一步验证该方案的可行性，让信道随机变化，观察本文算法是否仍能有效工作.

4.3 实验结果

4.3.1 信道规律变化

信道变化按照4.2中的设置进行，对本文算法得到的结果进行分析，图2(a)和(b)分别给出迭代次数为400和700次时，通信数据包的RBE情况.可以看出，随着迭代次数的增加，RBE超过0.1的次数明显减少.

在700次迭代后，算法收敛，得到策略π.当某一状态出现后，接收端记录该状态和奖励值，并反馈到发射端，发射端即可根据下一状态和策略π选择最优调制方式.根据策略π进行调制方式的选择并统计每次接收数据包的RBE和最终得到的Φ,结果如图3所示.可以看到在整个发射过程中，所有的数据包的RBE都低于0.1，且总吞吐量最大，达到了131 411 bit.同时加入通信过程中随信道变化所采用的通信制式表，如表2所示，随着信道条件逐渐恶劣，所选择的调制方式从高速率制式逐渐切换到了稳健的低速率制式.

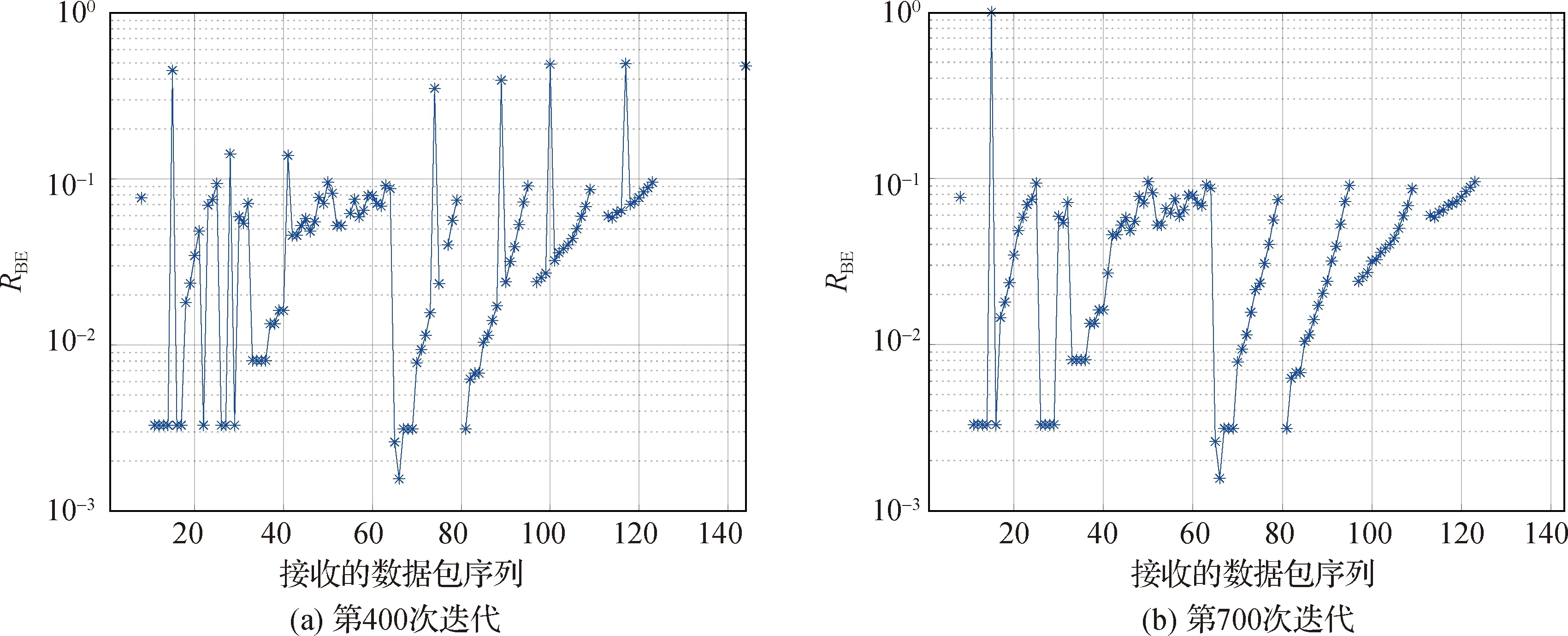
图2 迭代过程中的RBE曲线Fig.2Curve of RBE in iterative process

图3 基于RUQL的自适应调制方案性能图Fig.3The performance of adaptive modulation scheme based on RUQL

表2 发射过程中每种状态下对应的调制方式

图4 自适应调制方案的误码率曲线对比图Fig.4Comparison of RBE of adaptive modulation schemes

同样的，将本文算法与Dyna-Q、QL算法和Sarsa算法，以及采用基于阈值判断的自适应调制方法[6]进行对比.结果表明：Dyna-Q和QL算法在嘈杂非平稳环境中，效果几乎接近一致.这是因为虽然Dyna-Q有效地提高了所有行动的学习率，但是由于反馈链路存在出错的情况，最佳行动的Q值在收到嘈杂的负奖励时可能会下降.然而，对于本文自适应算法，虽然反馈链路出错带来的奖励负值同样会导致RUQL的Q值下降，但一旦误码率低于0.1的行动被尝试且反馈链路不出错，RUQL将提高该行动的学习率，从而更快地从该效应中恢复过来.同时，RUQL的促进作用随着行动的选择越来越频繁而减弱，学习在嘈杂时变得稳定，从而导致其性能高于其他算法.另外，正如前文所分析的，由于Sarsa算法比较保守，其性能低于QL、Dyna-Q和本文算法；固定阈值自适应算法由于反馈延迟问题，在所有自适应调制算法中性能最差.Dyna-Q自适应调制法最后得到的系统总吞吐量为129 647 bit.基于QL算法的自适应调制方法能达到的系统总吞吐量为129 743 bit.基于Sarsa算法的自适应调制方法能达到的系统总吞吐量为128 633 bit.而基于固定阈值判断的自适应调制方法最终的总吞吐量为125 862 bit.如表3所示，在系统吞吐量上，本文算法相较于Dyna-Q、QL、Sarsa和固定阈值判断的自适应算法分别提升了1.4%、1.3%、2.2%和4.4%.其余单一制式算法，随着信道条件变差，误码率逐渐超过0.1，故系统吞吐量不再随着接收数据包序列增加而提升.

表3 自适应算法效果对比表

固定阈值判断、Dyna-Q、QL和Sarsa算法的误码率对比曲线如图4所示，可以看出，4种算法中，还有不少误码率大于0.1的情况出现.

4.3.2 信道随机变化

接下来，让信道随机变化，统计各种制式的误码率和系统总吞吐量.信道RSN和多普勒具体变化如图5所示.从图6可以看出，在随机的信道变化状态下，RUQL的误码率始终保持在0.1以下，而其他自适应调制算法都出现了误码率大于0.1的情况.且如图7所示，本文自适应调制方案实现的系统吞吐量始终保持在最高，本文提出的算法相较于其他自适应调制算法方法仍能保持较好的性能.

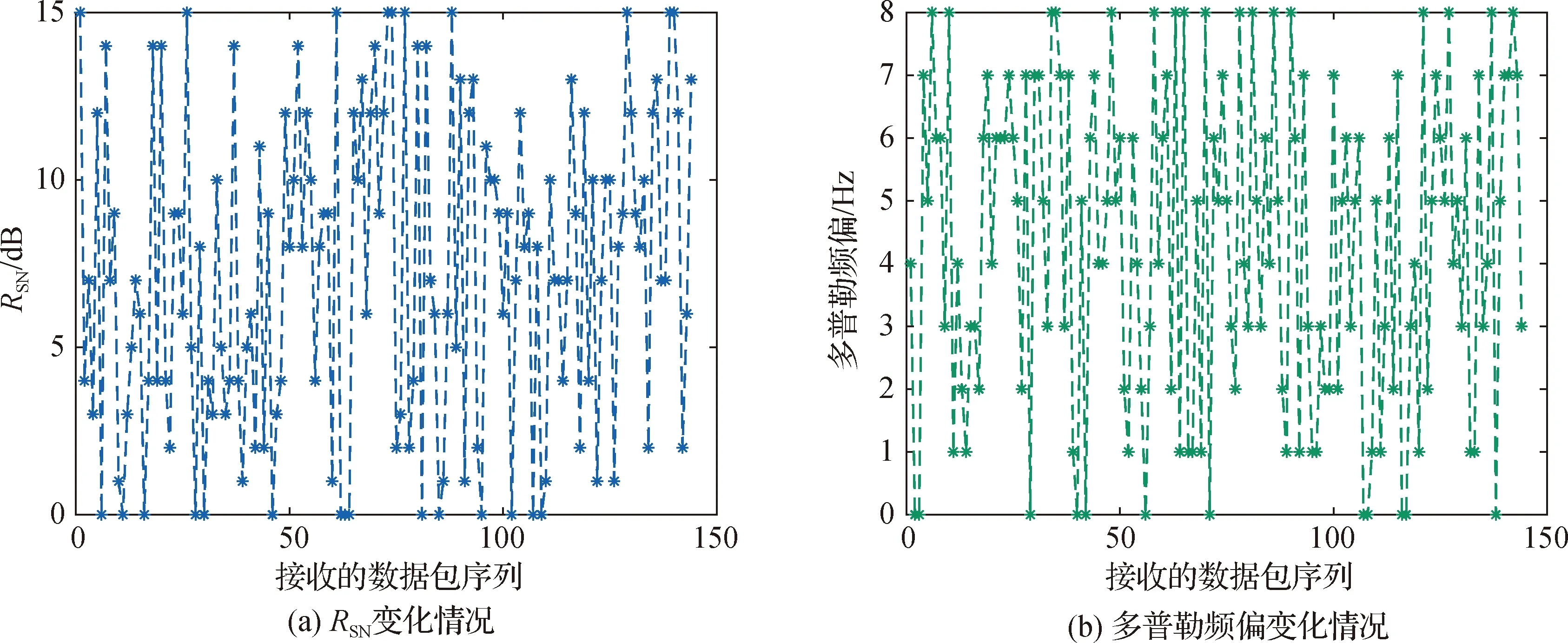
图5 随机信道状态变化情况Fig.5The changing process of random channel state

图6 信道随机变化下各种自适应调制方案性能图Fig.6The RBE of several adaptive modulation scheme under random channel variation

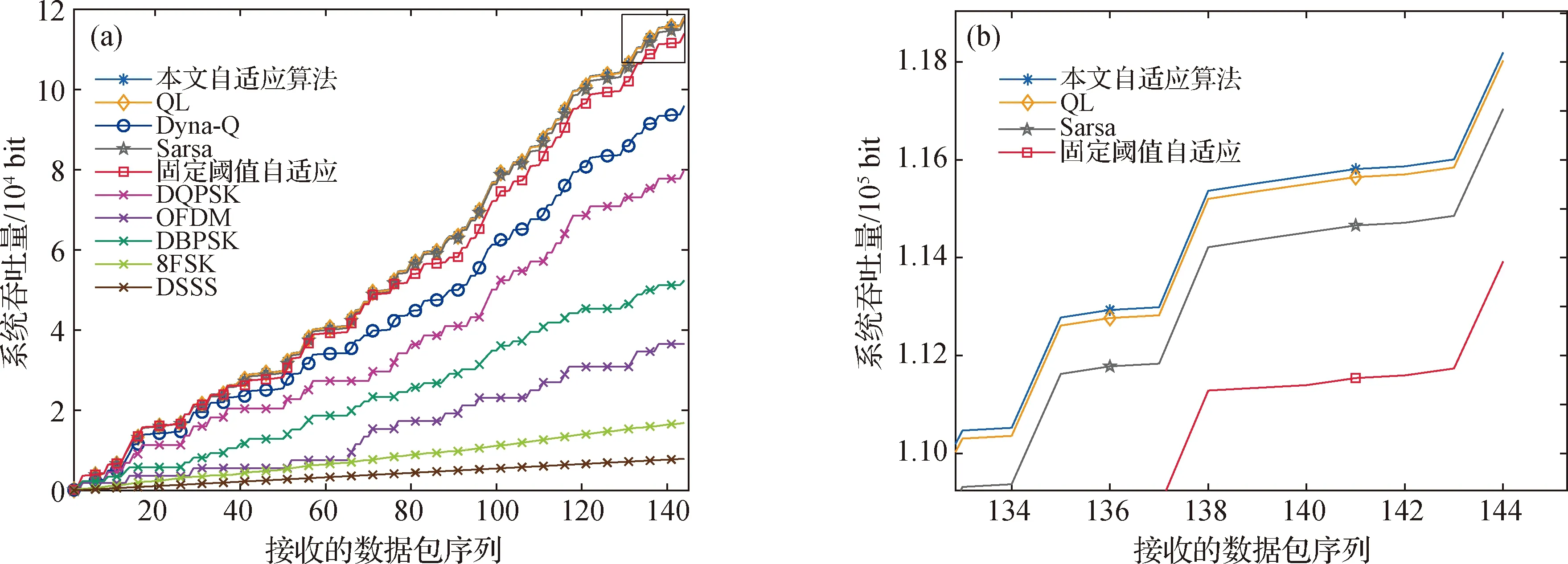
(b)为(a)中右上角方框的放大图.图7 信道随机变化下各种自适应调制方案的性能图Fig.7The performance of several adaptive modulation scheme under random channel variation

5 结 论

本文设计了一种基于RUQL算法的浅海水声通信自适应调制技术方案，采用RSN和多普勒频偏作为表征环境状态的要素，在DQPSK、OFDM、DBPSK、8FSK、DSSS 5种通信制式中进行优化选择，综合误码率和系统吞吐量设计了相关的奖励函数.实验结果表明该方案相较于传统方法能获得更好的误码率和系统吞吐量.基于本文获得的初步结论，下一步将开展不同浅海信道条件下的实验评估，从而对所提方案进行更充分的有效性分析和性能对比.