基于偏置采样和包围优化的移动机器人路径规划方法

陈彦杰，梁景林，张智星，喻 骁，王耀南

(1.福州大学机械工程及自动化学院，福建福州350108；2.厦门大学航空航天学院，福建厦门361102；3.湖南大学电气与信息工程学院，湖南长沙410082；4.机器人视觉感知与控制技术国家工程研究中心，湖南长沙410082)

现如今，移动机器人已广泛应用于生活中的不同领域，例如物流运输[1]、服务机器人[2]、场所消毒消杀[3]等.路径规划是移动机器人进行任务作业的关键环节，其主要作用是为机器人提供一条从起始点到目标点的连续路径.该路径在保证安全无碰撞的前提下，还能满足任务所约束的一些条件.目前，普遍使用的规划方法包括神经网络法、蚁群算法、势场法和随机采样法等[4-7].

基于采样的规划方法由于能够给机器人快速地提供可行路径，因此得到了广泛的关注.快速探索随机树(rapidly-exploring random tree，RRT)[8]通过在搜索空间中持续采样单个状态从而增量地扩展到目标状态，得到可供机器人行驶的无碰撞路径.Klemm等[9]提出了RRT-connect，分别从起始点和目标点扩展双向的搜索树，能够快速地找到一条可行路径.RRT方法虽然计算效率较高但所获得的路径通常并非最优，使机器人需要较多时间才能到达目标.针对这一问题，Karaman等[10]在RRT方法的基础上加入了重布线过程(rewire)和路径代价(cost)函数，对已有搜索树中的节点和节点间连接进行选择改进，使其拥有渐进最优的性能，得到了RRT*方法.由于RRT*方法在搜索阶段覆盖扩展了整个空间，造成探索效率的不佳.因此，知情RRT*(informed RRT*)方法[11]设计了知情集(informed set)，用于在找到初始路径后将采样范围限制至一椭圆区域，从而减小搜索范围，使得路径能够更快地收敛到最优解.快速行进树(fast matching tree，FMT*)方法[12]综合了概率路线图[13]和RRT，利用一批采样点进行树状扩展，但FMT*容易出现冗余探索，从而导致路径搜索性能较低.吴铮等[14]提出了一种基于方向选择的启发式函数，评估样本的代价梯度，调整样本排序，引导FMT*的扩展.基于安全通道的FMT*(ST-FMT*)[15]在方法扩展前增加了预处理生成初始路径，而后建立安全通道进行采样加速算法收敛.

批处理知情搜索树(batch informed trees，BIT*)[16]结合了Informed RRT*和FMT*的部分特点，通过多批次采样进行探索树的扩展.BIT*的采样在知情集所确定的椭圆区域进行，其采样点的扩展和连接顺序由各点的代价估计值排列.Liu等[17]提出一种贪婪搜索策略对边的连接顺序进行优先处理，能更快找到初始解.Strub等[18]通过使用非对称双向搜索来估计适用于不同问题的启发式，有效提高了初始路径寻找效率.这些方法都加快了BIT*对于初始路径的获取，但初始路径并非都是趋向于最优路径所在区域，并且对后续路径的改进有所欠缺.

因此，为了提高BIT*的规划效率并加快路径代价降低速度，本文提出了一种基于偏置采样与包围优化的BIT*(wrapping-based biased BIT*,WB-BIT*)方法.该方法包括了两个策略：1) 路径包围优化，对当前搜索所得的现有路径进行处理，使其包围至障碍物附近，以此降低路径代价，进而减小知情集区域；2) 路径指导偏置采样，利用当前路径点的信息，生成偏置采样区域加速更优路径的搜寻和路径代价下降速度.最后，本文通过仿真实验的实现和结果的对比分析，验证了WB-BIT*方法的有效性和高效性.

1 WB-BIT*方法

为解决BIT*方法中存在因路径代价下降速度慢导致规划时间长、效率不佳的问题，本文提出了WB-BIT*方法.

1.1 函数定义

路径规划是指在地图中寻找到一条安全且可行的连接起始点和目标点的路径.对于移动机器人，其路径代价可等同于移动的距离，因此在本文后续章节中使用路径长度代表路径代价.定义X∈Rn表示为移动机器人的状态空间，n为搜索空间的维度.BIT*方法在状态空间里呈树状增量搜索，采样点连接至搜索树后成为节点v，两节点间的连接称为搜索树的边.搜索树T包含了节点集合V和边集合E，即T=(V,E).定义搜索树T中起始点xstart到目标xgoal的最优路径长度为cbest,当前路径长度为ci,未找到可行路径时ci=∞.

1.2 WB-BIT*方法主要模块

WB-BIT*方法的整体结构框架具体如算法1所示，其中包含了以下几个主要模块：

1) 批量均匀和偏置采样.WB-BIT*方法首先在整个搜索空间中随机均匀采样；当获得初始路径后，以目标点和起始点为焦点，初始路径长度作为长轴长度构建的椭圆区域称为知情集，如图1所示；当知情集确定后，采样则在此椭圆区域中进行，该区域会随当前最优路径长度的减少而逐步缩小.本文设计了基于路径指导的偏置采样，与当前椭圆区域的均匀采样相结合，以此减少原始椭圆区域中可能存在的冗余样本，同时有效利用路径信息，提高探索路径的效率，即算法1中第7行.

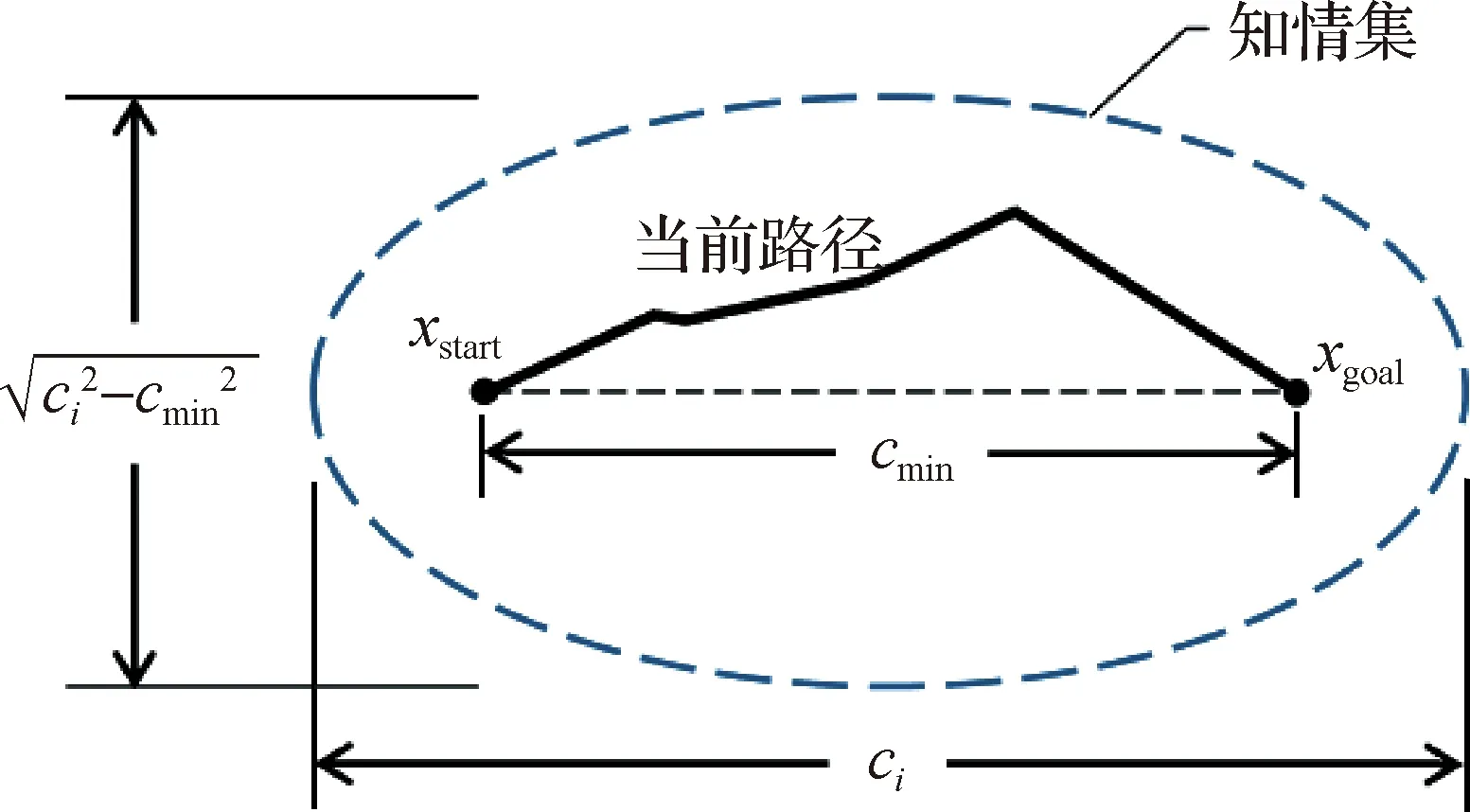
图1 知情集采样区域Fig.1Informed set sampling region

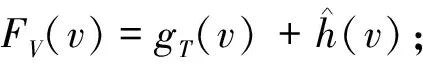
rBIT*≥

(1)

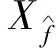
3) 节点与边的扩展和路径优化.选择的边(vmin,xmin)在通过启发式和碰撞检测的判断后，才会进行实际扩展，连接并加入搜索树中(算法1第13～23行).此时若点xmin已存在于搜索树中，则认为是树的重布线过程，否则该点加入节点集合V，并判断其是否能连接至目标点，若能连接，即可输出一条可行路径及其长度.本文设计了一种路径包围优化策略，每当路径长度发生变化时能够利用该策略将当前路径快速包围至障碍物周边，使路径长度快速减少，有效缩小知情集的椭圆区域，从而提高搜索精度(算法1第20行).

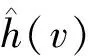
算法1WB-BIT*

1：V←{xstart};E←∅;T←(V,E)

2：Xunconnected←xgoal

3：QV←V;QE←∅

4： repeat

5： ifQE=∅ andQV=∅ then

6：Xreuse←Prune(T,Xunconnected,ci)

7：Xsampling←Hybrid_Sample(m,xstart,xgoal,ci,Xpath)

8：Xunconnected←Xreuse∪Xsampling

9：QV←V

10： While Best_Value(QV)≤Best_Value(QE) do

11： Expand(QV,QE,ci)

12： (vmin,xmin)←Pop_Best(QE)

15：cedge←Collision_checking(vmin,xmin)

22： else

23：QV←∅;QE←∅

24： until STOP

25：returnT

1.3 路径包围优化

在路径规划过程中，知情集是通过当前最优路径长度决定采样区域的大小，而更小的采样区域能够提供更精细的搜索.因此，为了通过减小采样区域实现更加精细的搜索和更短路径的获取，本文设计了一种基于当前路径包围障碍物的路径优化策略.该优化策略主要流程如算法2的伪代码所示.

算法2Path_Optimization(Xpath,r)

1：i←1

2：Pnum←|Xpath|

3： Whilei<(Pnum-2)

4：d←Max(‖xi-xi+1‖2,‖xi+1-xi+2‖2)

5：U=round(10·d/r)

6：d=(xi-xi+2)/U

7： if LocalPath(xi,xi+2)∈Xfreethen

8：Xpath←Xpathxi+1

9：i=i-1

10： break

11： else

12： forj=1 to (U-1) do

13：xtemp=xi+(xi+1-xi)·j/U

14： if LocalPath(xi,xtemp,xi+2)∈Xfreethen

15：xi+1=xtemp

16： break

17： else

18： fork=1 to (U-j) do

19：xnew=xtemp+δ·j

20： if LocalPath(xi,xnew,xi+2)∈Xfreethen

21：xi+1=xnew

22： break

23：i=i+1

24： returnXpath

算法2的路径优化策略在路径长度有更新时执行.策略开始执行后，当前路径根据自定义变量被离散为均匀配置，由目标点至起始点将路径包围至障碍物周围.算法2伪代码中的LocalPath()函数表示节点之间连线的碰撞检测，|Xpath|表示路径点集合的基数，若路径中包含N个点，则Xpath={x1,x2,…,xN}.此外，算法2中U是路径连接的离散化程度，根据当前连接半径与自定义变量的比例来确定，能在路径点连接大于连接半径时更精细地进行路径优化.

图2展示了一个简单的路径优化示例，图2(a)黑色实线为原始路径.首先拟连接xgoal和x1(蓝色虚线)，当此连接发生碰撞时，通过均匀离散化拟连接直到x′2与x1和xgoal的连接均在可行区域(图2(b))，此时x′2替换x2作为新的连接，如图2(c)红色实线所示.然后重复类似过程得到x′1,最后得到图2(d)所示的新路径.显然，由于三角不等式中第三边小于其余两边之和，优化后的路径具有更短的长度.

图2 路径包围优化过程Fig.2Wrapping process of path optimization

1.4 基于路径指导的偏置采样

路径优化策略能够加速当前路径长度的减少，获得一条高质量路径.当环境中存在多条路径时，则需要保持对潜在更优新路径的探索.因此，本文设计了一种采样策略，利用当前路径点相关的启发式函数值计算搜索区域，执行偏置采样.

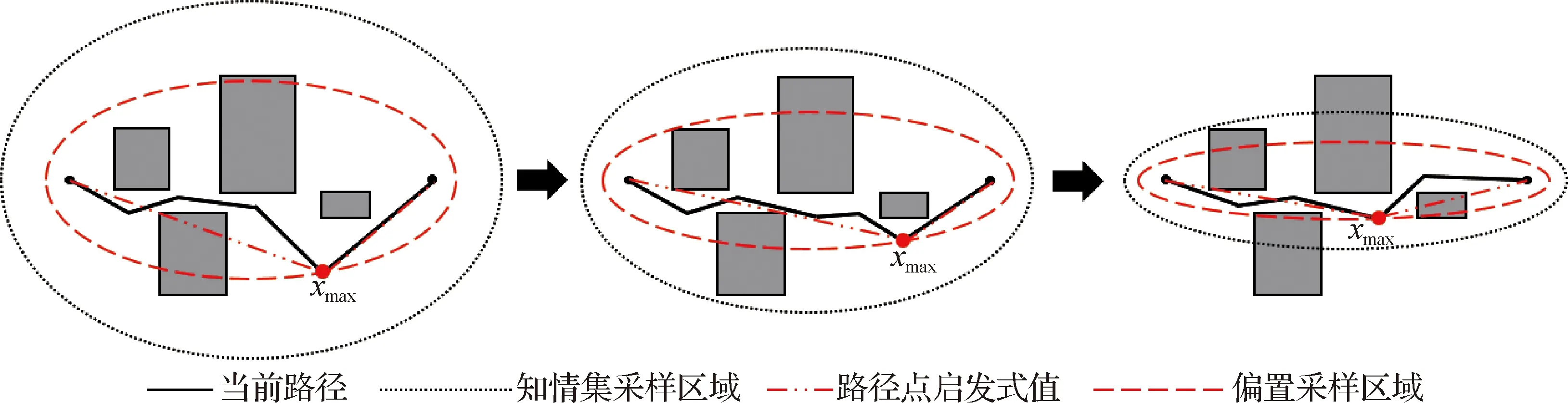
图3 知情集采样与偏置采样Fig.3Informed sampling and biased sampling

WB-BIT*方法探索初期未找到路径时，路径长度视为无穷大，采样在整个搜索空间中随机均匀进行.当获得一条可行路径时，偏置采样策略才会执行.可行路径是由各路径点连接而成，可表示为Xpath={xstart,x1,x2,…,xgoal},策略首先计算各路径点的启发式值：

‖xgoal-x‖2,(x∈Xpath),

(2)

(3)

其次取各点启发式值中最大值H(xmax)作为偏置采样的参数，使用H(xmax)作为椭圆长轴的长度，起始点xstart和目标点xgoal作为焦点建立一个椭圆的偏置采样区域，如图3所示.所建立的偏置采样区域属于知情集的子集，在路径数量不止一条的情况下，从这个较小子集中进行采样，更有可能找到改善路径和加快算法收敛的采样点.然而，由于该采样区域是通过现有路径进行估计的，所含信息不如知情集充足，可能得到的是局部最优路径[19].因此，为了确保WB-BIT*方法的采样均匀性而保证渐进最优性，偏置采样需要与知情集采样结合，并引入偏置比α∈(0,1)来平衡这一采样过程(如算法3第7行).当已有可行路径时，在偏置区域生成样本的概率为α,在知情集中进行采样的概率则为1-α.偏置采样的伪代码如算法3所示.

算法3Hybrid_Sample(m,xstart,xgoal,ci,Xpath)

1：Xsampling←∅

2： repeat

3： ifci<∞ then

4： forx∈Xpathdo

7： ifα>rand() then

8：Xsampling←Sample_Informed(xstart,xgoal,ci)

9： else

10：Xsampling←Sample_Bias(xstart,xgoal,H(xmax))

11： else

12：Xsampling←Uniform_Sample(X)

13： until |Xsampling|=m

14： returnXsampling

1.5 理论分析

本小节对WB-BIT*方法进行理论分析.

定理1概率完备性.对于待解决路径规划问题，若该问题存在解，则当方法的迭代次数或搜索时间趋于无穷大时，获得一条从起点到终点的可行路径解的概率为1，即：

其中:q是采样点的数量，σq是从这些采样点中找到的路径，Σ是所有可行路径的集合.

证明WB-BIT*是基于BIT*方法的改进，通过节点扩展和连接增量地生成连续的树.该方法在进行规划过程中，起始点xstart和目标点xgoal在搜索空间中位置是已知的.在未有可行解存在的时候，该方法不断地在整个空间中批量均匀采样，并通过启发式的估计值递增地从xstart连接各采样点.当规划问题存在解时，由于批量采样均匀地逐渐覆盖整个搜索空间，最终xstart将通过采样点无碰撞地连接至xgoal,因此找到一条可行路径解的概率为1.基于上述论点，WB-BIT*具备概率完备性.

定理2渐进最优性.当采样至无穷个样本时，WB-BIT*方法渐进收敛到给定路径规划问题的最优解的概率是1，即：

其中:q是采样点的数量，σq是从这些采样点中找到的路径，c(σ*)代表理论最优路径长度.

证明对于一个采样序列Xsamples={x1,x2,…,xq},WB-BIT*考虑了至少和RRT*相同的边和连接半径.RRT*从采样序列中的某个样本增量地构建一棵搜索树.该序列中的每个采样点xk∈Xsamples考虑了连接半径内的所有邻点：

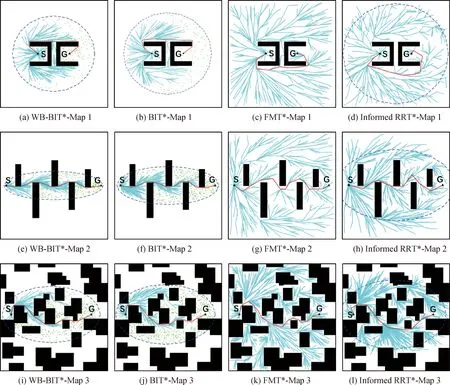
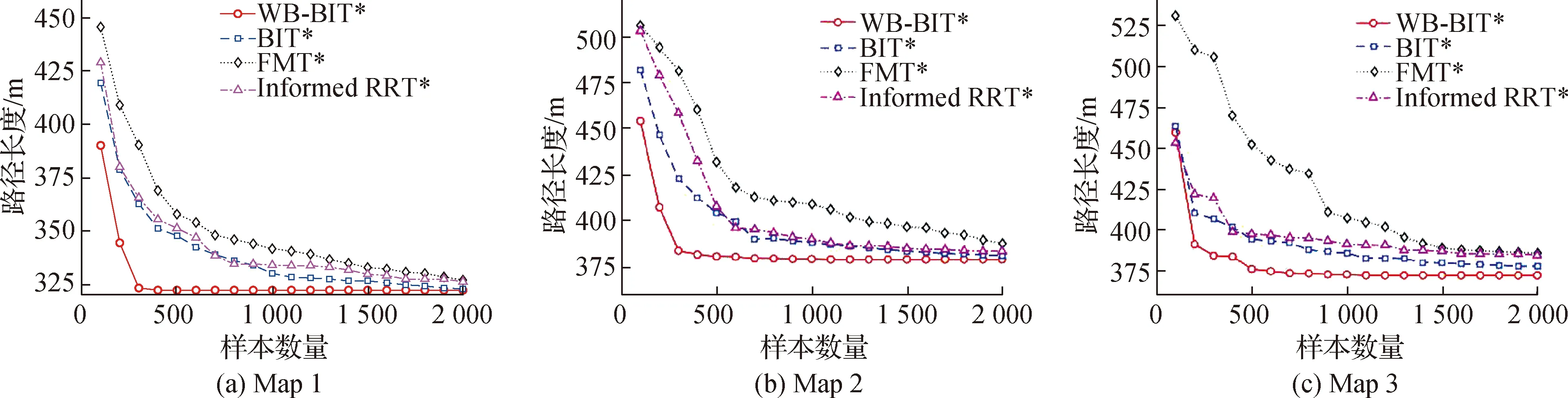
Xnear,k={xj∈Xsamples|j

rRRT*}.

图4 仿真实验环境Fig.4Experiment environments

采样点xk从这些邻点中选择能够使得xk的当前实际gT(xk)最小化的状态进行连接，接着经重布线考虑其余邻点能否通过连接xk使各自当前gT(xother)降低.

给定相同的采样序列，WB-BIT*将采样序列分为批量样本，Xsamples={Y1,Y2,…,Yl}.其中每一批样本是q个采样点的集合，例如Y1={x1,x2,…,xq}.WB-BIT*通过处理该采样序列中每一批样本，递增地构建搜索树.对于集合y∈Yk中的每个采样点，均同时考虑了整个采样序列中处于连接半径内的所有邻点：

Xnear,k={x∈Yj|j

这些采样点通过与邻点的连接，将边添加到搜索树，使得当前实际gT最小化，并考虑连接范围内其余边连接至它的邻域.这组边的集合包含了RRT*在其连接范围内所考虑的所有边.给定RRT*连接半径：

(4)

结合式(1)WB-BIT*方法的连接半径，由于WB-BIT*在任一批次样本中的连接半径与RRT*方法在该批次中第一个样本的连接半径相同，且两者的连接半径均单调递减，说明了WB-BIT*至少考虑和RRT*相同的边，同时WB-BIT*从这些边中选择能够降低搜索树中节点代价，并能够提供更好的路径连接.因此结合以上说明和Karaman等[10]对于RRT*渐进最优性能的论述，WB-BIT*也是具有渐进最优的性能.

2 仿真实验与分析

2.1 实验环境设置

仿真实验在MATLAB R2018b软件中进行，计算机平台为Windows 10操作系统，i7-7700HQ处理器和16 GB运行内存.为了验证WB-BIT*的有效性和高效性，将其分别与BIT*、FMT*、Informed RRT*方法在不同场景下进行仿真对比.

仿真对比在3个不同场景下进行，Map 1～3均为静态地图，如图4所示.其中S代表起始点xstart,G代表目标点xgoal.Map 1为起始点和目标点均有环绕障碍物的场景；Map 2为多条可行路径地图，其中一条为最优路径所在区域；Map 3为复杂场景，存在许多障碍物.3个场景的理论最优路径长度c*分别为320,378,372 m，当方法运行到路径收敛效果(当前路径长度/理论最优路径长度)小于1.05时终止，此时视作完成规划，并同时记录样本数量、搜索时间、路径长度等数据.所有场景地图中每个方法均进行30次实验，并使用30次实验的数据平均值作为最终结果，WB-BIT*的偏置比α设置为25%.

2.2 实验结果与分析

图5分别为在样本数为500(Map 1)、500(Map 2)、1 000(Map 3)时各规划方法的结果.红色连线为当前路径，蓝色椭圆边界线为知情集区域.从图中可以看出，各方法都能够找到一条可行路径，但所得路径的长度存在差异.当WB-BIT*找到一条路径时，通过路径包围优化策略能够使此路径靠近至障碍物边缘，快速地减少路径长度.同时偏置采样策略能够对后续采样和路径的进一步改善起到有效作用，尤其是处于Map 2和Map 3这种存在多条可行路径的场景中.在样本数量的限制下，本文所提出的WB-BIT*能够获得比其他对比方法更优的路径.

图5 不同场景地图中各方法的规划结果Fig.5Planning results of each algorithms in different maps

此外，将方法运行终止时所记录的数据，即收敛效果、路径长度、搜索时间和样本数量作为性能指标进行对比分析，如表1所示.从表1的数据中可知，当各规划方法收敛效果均小于1.05时，WB-BIT*在3个不同地图中获得趋近于理论最优路径的所需样本数量和消耗时间较少.在Map 1中，环绕障碍物造成知情集椭圆区域过大，BIT*和Informed RRT*都存在冗余探索的问题，需要通过更多样本数量才能更新到较优路径.WB-BIT*的路径包围优化策略能够使路径靠近至障碍物周围，并利用偏置采样进行路径的完善，最终通过较少的样本数量趋近于理论最优路径.在Map 2和Map 3中均存在多条可行路径，WB-BIT*的策略使其能够将搜索到的路径长度快速降低以减小知情集区域，同时偏置采样的存在能够进行潜在更优路径的搜索.最终结果WB-BIT*都优于对比的BIT*、FMT*、Informed RRT*方法.

为了进一步分析方法的规划效率，在图6中给出了不同地图下样本数量与路径长度的关系图.WB-BIT*在所有地图中样本数量较少的情况下，路径长度均具有较快的减少速度.以Map 1为例，WB-BIT*方法使用300个样本，得到了距离理论最优解1%内的路径长度，所需时间3.316 s(表1)，其他几个方法则需要更多的样本和时间才能达到相近的收敛效果.

表1 不同地图仿真实验结果

综上所述，仿真结果验证了WB-BIT*在不同环境下能够高效地完成路径规划，且相较于同类规划方法具有较快的路径长度减少速度和良好的寻路效率.

图6 不同规划方法的路径长度与样本数量关系图Fig.6Relationship between path cost and sampling numbers of different planning algorithms

3 结 论

为了解决BIT*方法存在的路径代价降低速度慢和探索效率不佳的问题，本文提出了WB-BIT*方法.路径包围优化能够在找到可行路径后，使路径包围至障碍物周边，达到快速缩短路径长度的目的.通过路径中节点的启发式值指导偏置采样区域的建立，协助潜在更优路径的寻找.方法的仿真结果也验证了WB-BIT*的有效性和高效性.未来的工作是将WB-BIT*拓展至动态环境，提高所用策略的环境适用性.