基于Matlab辅助的“计算机控制技术”教学方法探讨:以“最少拍控制系统”设计为例*
朱家骥,李爱琴,段小汇
(盐城工学院电气工程学院,江苏 盐城 224051)
“计算机控制技术”是自动化类专业的核心课程之一,涉及的知识面广,知识集成度高,在专业课程体系中占举足轻重的地位。近年来,随着计算机技术、控制技术、信息技术、通信技术的不断发展及其相互之间的渗透和影响,极大地推动了计算机控制技术的迅猛发展。同时,以计算机控制技术为基础的计算机控制系统在军事、工业、农业、交通运输等各个领域获得了广泛的应用[1]。基于这样的应用需求,社会对掌握计算机控制技术的高素质人才的需求不断扩大。由此可见,“计算机控制技术”课程教学效果的优劣对自动化类专业学生综合应用能力的培养会产生直接影响。
1 课程特点及教学方法探讨
“计算机控制技术”是一门理论性和实践性都很强的综合性课程,与“模拟电路”“数字电路”“单片机原理与技术”“微机原理与接口技术”及“自动控制原理”等诸多专业课程都有关联[2]。它主要包含2部分内容:①计算机控制理论基础。该部分内容包括采样定理、Z变换、脉冲传递函数、离散系统分析、数字控制器设计方法等。②实现技术。该部分内容包括模拟量输入与输出通道、数字量输入与输出通道、数据处理与数字滤波等。这其中,计算机控制理论概念抽象、公式变换烦琐、数学计算量大,学生在学习过程中普遍反映理论知识枯燥,难以理解和掌握[3]。因此,对于“计算机控制技术”任课教师而言,选择合适的教学方法和手段是非常重要的一项任务与挑战。
本课程的教学目标是希望学生能够掌握计算机控制系统设计的步骤、方法以及分析问题、解决问题的能力,很显然,通过单纯的板书讲解很难实现这一教学目标。鉴于此,借助软件进行辅助教学是非常有必要的,考虑到Matlab软件具有强大的数值、符号运算及图形处理等功能,目前已成为大学教学中常用的计算机辅助教学软件。因此,本课程尝试在课堂教学中采用传统板书讲授理论为主、Mtalab软件仿真为辅的模式,在此基础上穿插实际案例分析的教学方法,使教学内容形象直观、易于理解,以期提高教学质量,促进学生学习的积极性与主动性[4]。
2 案例分析
2.1 最少拍控制系统设计
最少拍控制系统设计是“计算机控制技术”课程的教学重点和难点内容之一,是控制器数字化设计方法的典型代表,在工业领域中最少拍控制系统常被应用于随动系统、伺服系统、运动控制系统等系统中[5]。最少拍控制系统设计的具体要求是:①最少拍控制器的设计是在给定输入信号的情况下进行的,且在到达稳态后,系统在采样点的输出值准确跟踪输入信号,不存在静差;②各种使系统在有限拍内到达稳态的设计中,系统准确跟踪输入信号所需的采样周期数应为最少;③最少拍控制器必须在物理上可以实现;④最少拍控制器与被控对象一起构成的闭环系统必须是稳定的[6]。
假设典型的数字控制系统框图如图1所示,在此基础上,最少拍控制系统设计步骤总结如下[7]。

图1 数字控制系统框图
步骤1,计算广义对象脉冲传递函数G(z),公式为:

步骤2,如果广义对象脉冲传递函数G(z)有l个采样周期的纯滞后,有i个单位圆上及圆外的零点z1,z2,…,zi,j个单位圆上及圆外的极点p1,p2,…,pj,则:

步骤3,先由式(6)和式(7)确定Φ0(z)和F(z)中z-l的最高次幂,其中m是由输入信号的类型确定的,如果输入信号为单位阶跃信号,则m=1;如果输入信号为单位速度信号,则m=2;如果输入信号为单位加速度信号,则m=3。然后将式(2)代入式(3)中,获得恒等式及其对应的方程组,计算确定Φ0(z)和F(z)中的参数。
步骤4,由Φ0(z)、F(z)以及广义对象的纯滞后时间、单位圆外的零点和极点确定Φ(z)和1-Φ(z)的具体表达式。
步骤5,计算最少拍控制器脉冲传递函数D(z),公式为:
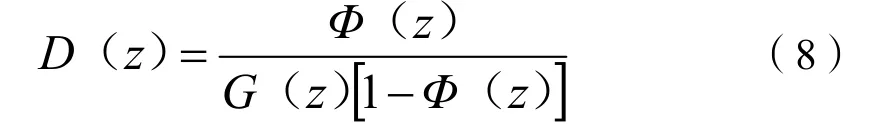
步骤6,计算系统输出信号的脉冲传递函数Y(z)和最少拍控制器输出信号的脉冲传递函数U(z),即:


式(9)(10)中:R(z)为输入信号的z变换。
虽然上述一般设计方法中考虑了被控对象有单位圆上零、极点(临界点)的情况,但由于系统中总存在阻尼,这些临界点是允许存在的。同时,考虑到设计的控制器不能过于复杂,故在上述步骤2中只考虑被控对象有单位圆外零、极点的情况,对被控对象单位圆上零、极点不做处理。
2.2 最少拍控制器解析法计算
系统的广义对象脉冲传递函如下:

由广义对象脉冲传递函数G(z)可知:G(z)无纯滞后环节,即l=0;G(z)无单位圆外的极点,即j=0;G(z)无单位圆外的零点,即i=0。由于本系统参考输入为单位阶跃信号,则m=1。由式(6)和式(7)可得s=1,t=0。
由式(2)可知,Φ(z)的表达式为:Φ(z)=Φ0(z),其中,由式(4)可知Φ0(z)=m1z-1,故Φ(z)=m1z-1。
由式(3)可知,1-Φ(z)的表达式为1-Φ(z)=(1-z-1)F(z),其中,由式(5)可知F(z)=1,故1-Φ(z)=1-z-1。
由2个独立表达式Φ(z)和1-Φ(z)可解得ml=1,故Φ(z)=z-1。在此基础上,可由式(8)得到最少拍控制器脉冲传递函数D(z)的表达式,即:

由式(9)可得系统输出信号的脉冲传递函数Y(z)的表达式,即:


由式(10)可得最少拍控制器输出信号的脉冲传递函数U(z)的表达式,即:

综上所述,由Y(z)可知,系统输出在一拍后达到无静差的稳态;由U(z)可知,虽然控制量是收敛的,系统是稳定的,但由于控制量是波动的,实际上输出量在采样点之间也是波动的,即系统输出存在纹波。
2.3 最少拍无纹波控制器解析法计算
最少拍控制器只能保证在采样点上的稳态误差为0,在许多情况下,系统在采样点之间的输出呈现纹波,这不但使实际控制不能达到预期目的,而且增加了功率损耗和机械磨损。系统输出在采样点之间存在纹波,主要是由控制量序列的波动引起的,其根源在于控制器的脉冲传递函数中含有非零极点。设计最少拍无纹波控制器时,处理这些非零极点的具体方法是:选择闭环脉冲传递函数Φ(z)除了按上述的方法进行外(以保证控制器的可实现性及闭环系统的稳定性),像处理单位圆外的零点那样,还应将广义对象脉冲传递函数G(z)在单位圆内的非零零点包括在Φ(z)中,以便在控制器的脉冲传递函数中消除引起振荡的所有极点。依据此思想,且在2.2节的基础上进行最少拍无纹波控制器的设计。
由2.2节中计算得到的广义对象脉冲传递函数G(z)可知,其存在一个单位圆内的零点z=-0.717,在设计最少拍控制器中,选择Φ(z)时并没有考虑该零点,从而使控制器的脉冲传递函数F(z)中有一负实部的极点z=-0.717,造成了控制量序列的上下波动。在设计最少拍无纹波控制器中,为了消除纹波,取Φ(z)=(1+0.717z-1)m1z-1。由于Φ(z)中z-1的幂次增加了一阶,所以1-Φ(z)=(1-z-1)(1+f1z-1)。
由此可以解出,ml=0.58,fl=0.42,故Φ(z)=0.58z-1+0.42z-2。在此基础上,可由式(8)得到最少拍无纹波控制器脉冲传递函数D(z)的表达式:
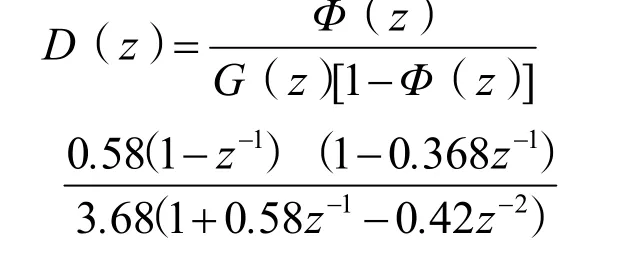
由式(9)可得系统输出信号的脉冲传递函数Y(z)的表达式,即:

由式(10)可得最少拍无纹波控制器输出信号的脉冲传递函数U(z)的表达式,即:

综上所述,系统的输出量序列为0、0.58、1、1、…,控制量序列为0.158、-0.058、0、0、…,系统在两拍之后才达到稳态,调节时间比原来的系统增加了一拍,但纹波却消除了,即控制量不再波动。
3 软件辅助设计与仿真
本节以图1所示的数字控制系统框图为基础,对第2节中所述案例采用Matlab/Simulink进行辅助设计与仿真。
3.1 最少拍控制器Matlab/Simulink辅助设计与仿真
由2.2节中最少拍控制器解析法设计过程可知,该方法设计步骤烦琐,计算量很大,任何一个步骤出现错误都将造成整个系统出现错误。实际上,最少拍控制器的设计完全可以由Matlab编程实现,Matlab编程实现的程序代码如下:

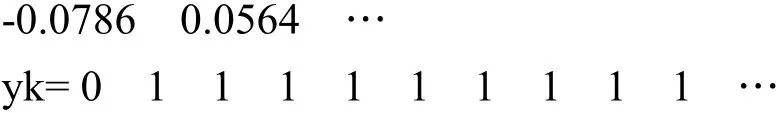
将上述结果与2.2节中解析法计算的结果进行对比,很明显,通过采用Matlab编程辅助设计的整个过程既快速,获得的结果又准确。同时,为了加深学生对理论计算方法的理解,可以采用Matlab中的Simulink功能对最少拍控制系统进行建模仿真。图2为本示例中最少拍控制系统的Simulink仿真实验模型,该模型运行后得如图3所示的仿真实验结果。
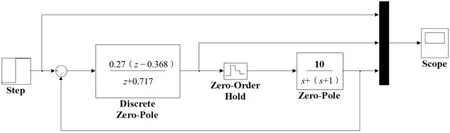
图2 最少拍控制系统Simulink仿真实验模型

图3 最少拍控制系统的输入、输出及数字控制器的输出曲线
图3采用Simulink建模仿真实验得到的最少拍控制系统的输入信号曲线、数字控制器D(z)的输出u(k)曲线和系统输出y(k)曲线。
如果单纯地进行理论推导与计算,学生对最少拍控制系统各环节输出的具体含义将很难理解,通过仿真实验输出的可视化效果,一方面使得输出结果更直观、更形象,另一方面有助于学生对最少拍控制器设计方法的理解与掌握。
3.2 最少拍无纹波控制器Matlab/Simulink辅助设计与仿真
由2.3节中最少拍无纹波控制器解析法设计过程可知,该方法设计步骤烦琐,计算量很大,故在本节中采用Matlab编程实现最少拍无纹波控制器的设计,Matlab编程实现的程序代码如下:


将上述结果与2.3节中解析法计算的结果进行对比,很明显,通过采用Matlab编程辅助设计的整个过程既快速,获得的结果又准确。
同时,为了加深学生对理论计算方法的理解,可以采用Matlab中的Simulink功能对最少拍无纹波控制系统进行建模仿真。图4为本示例中最少拍无纹波控制系统的Simulink仿真实验模型,该模型运行后得如图5所示的仿真实验结果,包括系统输入信号曲线、数字控制器D(z)的输出u(k)曲线和系统输出y(k)曲线。

图4 最少拍无纹波控制系统Simulink仿真实验模型

图5 最少拍无纹波控制系统的输入、输出及数字控制器的输出曲线
4 结束语
通过对“计算机控制技术”课程特点的分析,探索了教学方法的改进措施,并在教学过程中付诸了实践。本文以最少拍控制系统(包括最少拍控制器和最少拍无纹波控制器)设计为教学案例,采用基于Matlab/Simulink的辅助设计与仿真实验,加深了学生对最少拍控制系统设计方法的理解,促进了学生对该方法的掌握,从学生现场真实的实验结果与课后作业情况以及期末考试中可以看出,取得了较好的教学效果。希望在今后的教学研究和教学实践中,能进一步探索出更好的教学方法,提高学生分析问题、解决问题的能力,达到“新工科”教育背景下自动化类专业的培养目标。

