内燃机车静液压传动系统故障诊断

王道红

（中车资阳机车有限公司，四川资阳 641300）

当前，为了提升机械的动力以及应用效果，较多的机车在设计与制造的过程中均会采用10D 型号的内燃机，同时搭配定向的传动基础制动系统，为设备营造更为安全、稳定的应用环境[1]。内燃机车以静液压传动系统作为控制核心，除了空气压缩机之外，机车中所有装置均是关联的，分布在制动框架中，以此来增强系统的实际运行效益[2]。

但是在实际应用过程中，由于液压传动程序的混乱，再加上执行指令的单一，常常会出现应用故障[3]。因此，对内燃机车静液压传动系统故障诊断进行分析与研究。考虑到最终测试结果的稳定性与可靠性，需要先结合内燃机车传动系统的应用需求以及标准，提取对应的故障特征，与此同时，制定更加灵活、多变的故障诊断结构，从多个方向对异常位置定位检测，获取精准的诊断数据，为后续系统的维护以及调整奠定基础条件[4]。

1 内燃机车静液压传动系统故障诊断方法设计

1.1 内燃机车故障特征提取

针对内燃机车的运行情况，利用传动系统获取相应的数据信息。部分机车在应用的过程中，齿轮存在脱轨或者不平顺的现象，再加上车体振动，加速度增强，极可能导致故障，因此，可以先通过加速度的变化情况，模糊分析故障的区域，提取相关的故障特征指标，具体如表1所示。

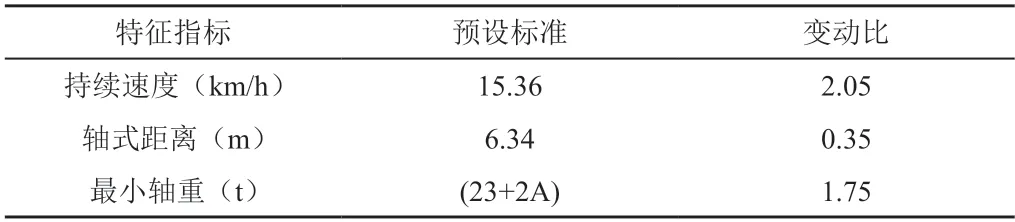
表1 故障特征指标参数表

根据表1，可以完成对故障特征指标参数的分析。随后，对传动系统故障区域的定向频率进行汇总[5]。此时，可以通过频谱的变动情况，二次定位出故障的区域，在范围之内提取不同种类的故障特征，以静液压传动的速度判断故障区域对关联设备的影响[6]。将获取的故障特征汇总整合，核定倍频系数[7]，完成故障诊断的基础工作。

1.2 ICA微小故障诊断节点布设

在完成对内燃机车故障特征的提取之后，需要针对于模糊的故障区域，进行ICA 微小故障诊断节点的布设。故障的位置与诊断节点的布设存在直接的联系，由于内燃机车的制动条件十分严格，一旦出现故障，便需要闭合执行电路，进行故障牵引。可以在标定范围内，以ICA 微小诊断程序组为节点，安装在内燃机车中，在合理静液压范围内，关联传动系统。计算诊断节点的单元距离，具体如式（1）所示。

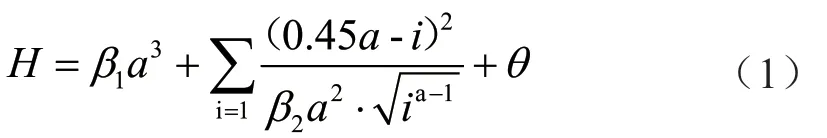
式中：H表示诊断节点的单元距离；β1表示承接传动范围；β2表示定向传动范围；a表示预设直径；i表示传动定向直径；θ表示极限误差。

通过上述计算，得出实际的诊断节点单元距离。根据单元距离，划定故障诊断范围。结合静液压的变动情况，缩小ICA 微小诊断节点的位置。这部分需要注意的是，每个ICA 微小诊断节点均需要与内燃机车的内控平台相关联，以此保证可以及时获取故障数据。

1.3 耦合牵引故障诊断模型设计

在完成对ICA 微小故障诊断节点的布设之后，需要设计耦合牵引故障诊断模型。根据内燃机车的啮合刚度变化情况，分析不同区域的故障比率，具体如式（2）所示。

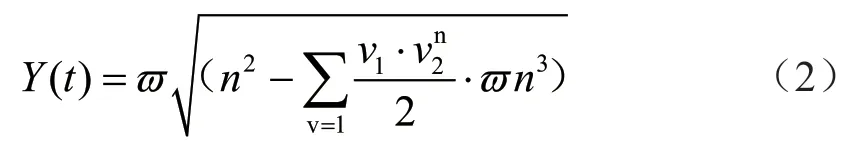
式中：Y（t）表示故障比率；n表示传动直径；v1表示振动频率；v2表示振动单元频率；表示线性诊断距离。

通过上述计算，最终可以得出实际的故障比率。采用拟态分析法，定位模糊区域中的故障点，利用耦合诊断框架建立牵引框架，传动系统中赋予动态预测目标，在多激扰、多工况状态下，依据故障特征，在耦合牵引模型中，构建定向耦合故障诊断程序，具体的诊断环节如图1所示。

根据图1，完成对耦合牵引故障诊断环节的构建。随后，利用获取的诊断数据，进行定向故障的分析，计算出牵引误差，具体如式（3）所示。

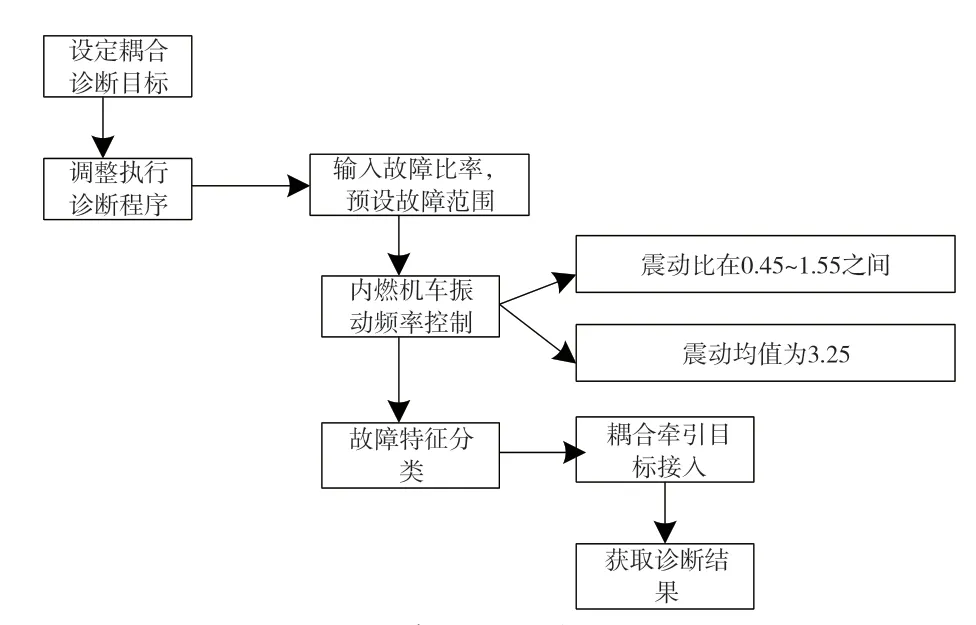
图1 耦合牵引故障诊断环节图示

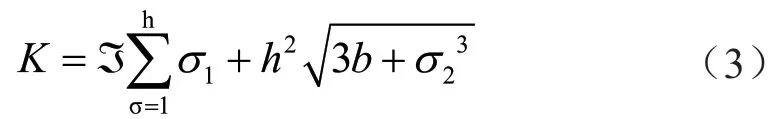
式中：K表示牵引误差；表示负载差值；σ1表示牵引频率；σ2表示牵引频率差值；h表示传动系数；b表示支撑阻尼。

通过上述计算，得出实际的牵引误差，将其作为诊断的标准，完成对耦合牵引故障诊断模型的设计。

1.4 恒定诊断矩阵设计

在完成对耦合牵引故障诊断模型的设计之后，需要针对于传动系统的特征，构建对应的恒定诊断矩阵。内燃机车在运行的过程中，内含的牵引电机-齿轮箱一旦受到外力的影响，极有可能发生故障的。针对于耦合故障电磁转矩频谱，计算出故障诊断的响应时间，具体如式（4）所示。

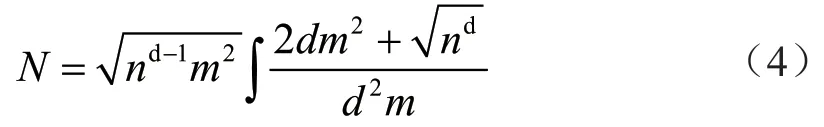
式中：N表示故障诊断响应时间；n表示电磁转矩频谱变动值；m表示频谱转换值；d表示转换系数。

通过上述计算，得出实际的故障诊断响应时间。构建恒定诊断结构，依据传动系统侦测的故障位置，调整对应的诊断目标。

需要注意的是，不同故障完成的诊断响应时间也是不同的，需要根据内燃机车的故障特征频率幅值变化情况来设定故障识别机制，实现故障定位。之后，系统会将诊断任务发送至对应的接收地址上，形成定向的诊断矩阵程序，获取首次的恒定故障诊断结果。

1.5 Bayes算法实现系统故障诊断

在完成对恒定诊断矩阵设计之后，需要采用Bayes 算法实现系统的二次故障诊断。利用ICA 微小故障诊断节点，获取相应的故障数据信息，在诊断矩阵之中，计算出单元内燃机车的逆变频率比值，与传动系统的诊断子模块相连接，建立综合统计量ESPE诊断程序。

这部分需要注意的是，为了更为精准地实现故障的识别，可以从多个方向关联故障诊断的监测节点，利用Bayes 算法计算出传动负载系数，并以对比的形式，获取诊断差值，计算出微小诊断误差，具体如式（5）所示。

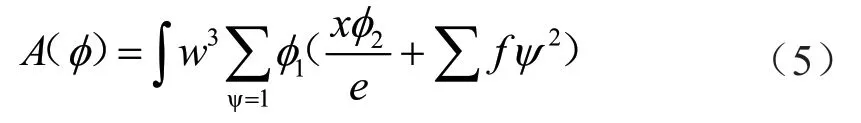
公式5中：A表示微小诊断误差；表示监测响应时间；表示诊断单元时间；w表示负载逆变值，表示恒定诊断范围；e表示牵引误差；x表示定向诊断绝对值；f表示测定响应时间。

通过上述计算，得出实际的微小诊断误差。利用故障诊断模型，获取最终的诊断结果。

2 方法测试

以传统制动系统故障诊断测试组、传统定向齿轮控制系统故障诊断测试组以及本文所设计的牵引液压传动系统故障诊断测试组展开对比测试。

2.1 测试准备

选择某中车企业作为测试背景，以企业内部所应用的内燃机车静液压传动系统作为测定目标。根据传动系统的执行指令，设定内燃机车设备的执行指标参数，具体如表2所示。

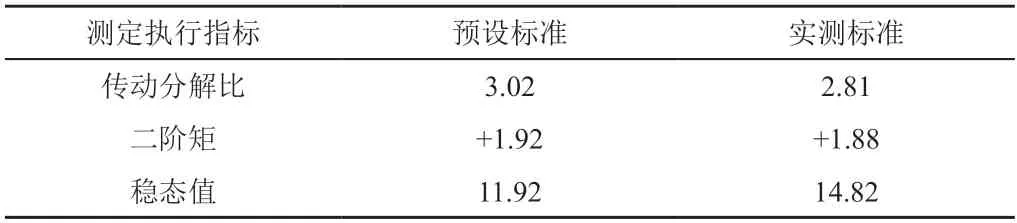
表2 内燃机车设备执行指标参数

根据表2可以完成对内燃机车设备执行指标参数的设定。随后，调整传动系统的内置数值，利用三维基础，模拟出对应的故障环境。

结合指令编制平台，将所需要设定的故障分类编制成三维目标指令，并设定在传动系统之中。避免对系统以及设备造成损坏，确保测试结果的精准。核定测试装置以及系统是否处于稳定的运行状态，同时确保不存在影响最终测试结果的外部因素，核定无误后，开始测试。

2.2 测试过程及结果分析

在系统中添加对应的故障指令，营造三维拟态故障环境。系统中设定的制动比为0.13，内燃机车的驱动变量为10.35，预设的驱动量为14.29，所出现的差值即为存在故障处形成的数据异常。可以先对传动系统异常数据处定位，并将应用中的设备从高电位调节至低电位，此时对于传动系统故障诊断的分解状态具体如图2所示。

根据图2可以完成对传动系统故障诊断分解状态曲线的设定。根据系统执行引导的相关拟态故障，结合定向的故障诊断模型，计算出诊断误差协方差，并进行具体分析研究，如表3所示。

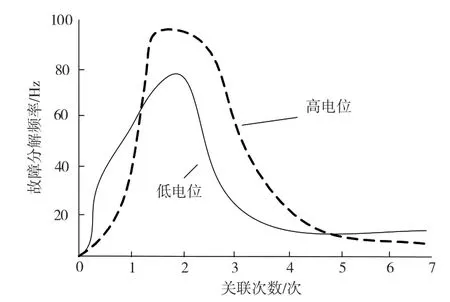
图2 传动系统故障诊断分解状态曲线图

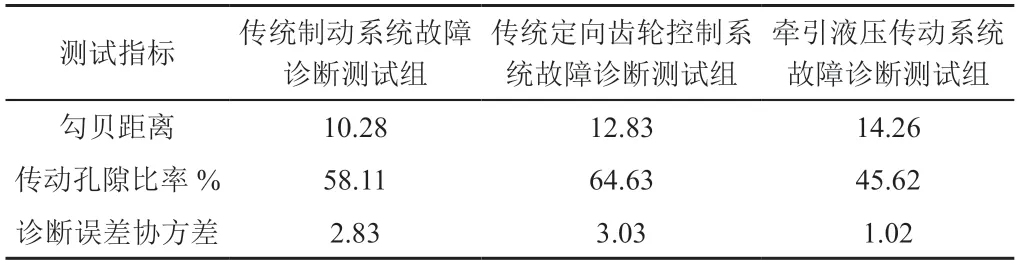
表3 测试结果对比分析表

根据表3，本文所设计的牵引液压传动系统故障诊断测试组最终得出的故障诊断误差协方差仅为1.02，与传统制动系统故障诊断测试组、传统定向齿轮控制系统故障诊断测试组相比，此种故障诊断方法在实际应用的过程中更为精准、误差较小，具有实际的应用价值。

3 结束语

对内燃机车静液压传动系统故障诊断进行研究以及分析。与传统的故障诊断方法相对比，本文所设计的传动系统故障诊断模式相对更加灵活、多变，在复杂的系统控制环境之下，可以通过多目标、多层次的分级诊断形式，将所发生的故障对于设备的损害降到最低，同时营造安全、稳定的执行环境，提升内燃机车的应用速率，推动传统系统实现进一步的创新。