基于ANP-BP神经网络的城市安全发展状态评估

张洋杰，杨云鹏，周 瑶，汪卫国，李 迪，徐承宇

（1.应急管理部研究中心，北京 100713；2.赛飞特工程技术集团有限公司，山东 青岛 266061；3.西安科技大学 安全科学与工程学院，陕西 西安 710054）

0 引 言

近年来随着中国城市发展进程的加快，城市在成为更加庞大和复杂系统的同时，安全事故也不断发生[1]。由于城市人口、资源和财产的聚集，发生的事故往往具有复杂性、传导性、扩散性等特征[2]。随着国家安全发展示范城市创建工作的开展和重视，标志着城市安全发展成为中国经济社会可持续发展的重要环节。

通过评估准确掌握城市安全发展状态是发现和应对城市安全问题的关键措施[3]。国外学者在城市安全评估方面，多从不同灾害入手，研究新兴评估方法或者结合不同学科角度进行综合评估[4-6]。ADAM引入风险修正指数（RCI），研究了更准确的城市风险分析方法[7]；RASTYAPINA等从社会、自然等方面对一个聚居区城市安全发展影响因素进行理论分析并分类[8]。国内学者多通过层次分析、因子分析等方法构建评估模型，有侧重地对城市的脆弱性、韧性等进行研究[9-11]。尹鑫伟等基于Petri网络和模糊推理算法分析城市安全发展状态评估方法[12]；刘继川等采用因子分析法构建风险评估模型并判别了影响武汉市城市安全的4个影响因子为城市发展水平和基础设施、事故灾害、环境影响和地质灾害及其防治[13]；李葛等基于PSR层次分析从系统压力、系统状态和系统响应3个方面构建指标体系并结合BP神经网络建立评价模型[14]；陈然等从政府视角研究了安全发展示范城市的创建方法并进行实例验证[15]。

目前，对城市安全发展状态的评估在权重设置中往往主观性过强，客观的评估方法往往存在关联度不够的问题，且评估对象比较单一。城市安全发展状态评估不同于简单的风险分析、安全评价或者脆弱性、应急能力等单因素评估，是以城市发展过程中从源头到措施的全方面安全问题作为对象的评估。鉴于此，文中以城市安全发展的相关理论为基础构建指标体系，采取ANP[16]和BP神经网络[17]相结合的组合赋权方法[18]，主客观相结合地计算出各级指标的组合权重，建立一种城市安全发展状态评估方法和模型，并通过实例计算证明模型的适用性。文中研究的评估模型对今后城市安全发展状态评估工作中的模型构建和方法选择具有一定指导意义。

1 指标体系构建

以科学反映城市安全发展状态为目标，综合考虑城市安全发展影响因素，并结合城市安全发展规划等相关要求，遵从指标体系构建原则，基于层次分析理论[19]综合系统地构建城市安全发展状态评估指标体系，如图1所示。其中城市安全发展状态包括城市安全源头治理、城市安全风险防控、城市安全监督管理、城市安全保障能力、城市安全应急救援5个一级指标，囊括城市安全问题从源头到防控再到事故发生后救援的全过程，同时从保障能力和监督管理进行多维度指标构建。将5个一级指标作为子目标构建20个二级指标，55个三级指标来更全面更深入地对城市安全发展状态进行评估。为了使指标体系具有可操作性与合理性，参考国际安全评级系统，根据相关国家标准、行业标准、法律法规和城市安全发展规划，采用“是否式”、“频率式”等5种量化方法对每一个基础指标进行了定量化分析和分级。

2 评估模型构建

为提高评估精准性，基于网络层次分析原理，采用专家打分法确定指标的主观权重；基于BP神经网络的基本原理和方法，使用MATLAB工具箱，确定指标客观权重；最后采用线性功效系数法，依据最小偏差将主客观权重进行组合得到指标的最终权重[20]，使该模型能够客观、定量地反映指标之间的相互关系，使评估结果更加科学、精确。

图1 城市安全发展状态评估指标体系Fig.1 Evaluation index system of urban safety development status

2.1 基于ANP法的权重确定

网络层次分析法[21]（ANP）是在AHP法基础上考虑多层结构、多个指标之间的相互耦合关系并进行改进的一种多准则决策方法，能够通过网络结构表示网络层各指标内部和外部的关系。

具体的求解过程如下。

2.1.1 构建网络结构

根据图1构建的城市安全发展状态评估指标体系，通过文献查阅和咨询应急管理领域专家确定城市安全发展状态的网络层次结构，如图2所示。

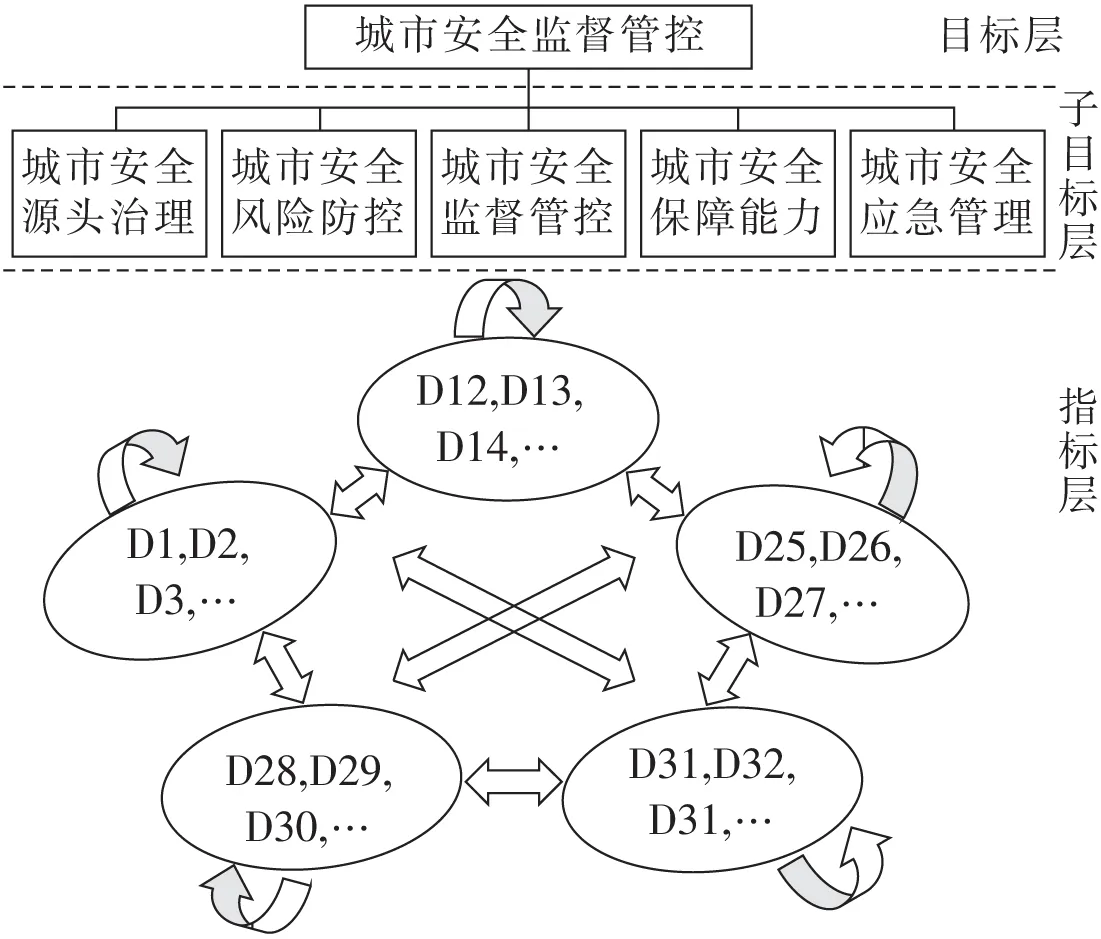
图2 城市安全发展状态ANP结构Fig.2 ANP structure of urban safety development status

2.1.2 重要度打分

根据各指标之间的相互影响关系制作问卷，并向城市安全与应急管理领域专家发放，专家通过重要度相对尺度表（见表1）对各层级和各评估指标之间的重要度比值进行打分。

表1 重要度相对尺度

2.1.3 计算各指标权重

1）构建未加权超矩阵。首先设定控制层中各准则元素分别为P1,P2,P3,…,Pm，其次设定网络层中各元素组为A1,A2,A3,…,An,Ai和Aj中所包含的元素分别为ai1,ai2,ai3,…,ain;aj1,aj2,aj3,…,ajn。以Pα（α=1,2,…,m）为计算准则，以Aj中的元素aj1为计算次准则，构建Ai中元素相对于aj1的判断矩阵。之后对构建的判断矩阵进行一致性检验[13]，得到权重向量[Wi1,Wi2,…,Win]T。其中，若一致性比率CR（Conformance Rate）小于0.1，则具有一致性。再以Aj中的元素aj2,aj3,…,ajn为次准则，构建A1中元素相互的判断矩阵，计算各矩阵的权重向量，得到子矩阵Wi1′，见式（1）

（1）

同理，可对各个元素间的关系进行一一对比计算，则可以求得各子矩阵，将所有子矩阵组合可构成为加权超矩阵W，见式（2）

（2）

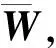
（3）

式中 矩阵M表示不同计算次准则下，准则层指标的判断矩阵所对应的权重向量组成的矩阵。

2.1.4 权重计算

根据求解指标权重值的过程，邀请专家对城市安全发展状态评估指标重要度进行打分，结合网络分析法构建的ANP结构图进行分析，借助SD（Super Decisions）[22]软件，构建各层级和各评估指标之间的网络关系图，输入专家打分结果可计算出未加权的超矩阵、加权超矩阵和极限超矩阵，从而可计算每个专家的初始权重结果。

2.1.5 权重修正

为尽量消除专家因素产生的误差，根据专家的专业技术级别、工作年限、学历等因素，对专家打分的可信度进行加权平均处理，从而得出各检查项目的最终评估指标的权重值。影响专家评分可信度的因素及取值，见表2。

第l位专家打分的可信度计算方法见，见式（4）

（4）

最后，将各专家的打分可信度进行归一化处理，便可得到专家打分的权重系数，见式（5）

（5）

式中k为专家总数。

结合初始专家各自的权重结果可得出最终的主观权重。

表2 影响评分权重的因素及对应权值量化

2.2 基于神经网络的权重确定

BP神经网络是神经网络中的一种典型网络结构，具有分层结构，信息从输入层进入网络，逐层向前传递至输出层，含有隐含层的多层前馈网络能够提高网络的分类能力。因此本模型以各指标得分作为输入层，通过主观权重计算的城市安全发展指数作为输出层，根据模型得到的隐含层数据则作为客观权重。

2.2.1 数据处理

1）标准化处理。在多指标评估体系中，各指标的性质、量纲和数量级各不相同，因此需要对原始数据进行标准化处理。将55个基础指标得分按照比例进行放缩，使每一个指标的得分均为0～100。

2）多元线性插值[23]。因收集城市的基础数据有限，但在采用基于神经网络算法构建的城市安全发展状态评估模型计算基本指标的客观权重时，模型输入数据过少可能导致模型拟合效果差、真实值与预测值误差过大等现象。因此采用线性多元插值法，每2个城市间插入12组数据，得到53组指标数据赋值。

2.2.2 BP神经网络算法建立[24]

1）激活函数选择。激活函数的显著功能是“去线性化”，提高整个网络的逼近能力，同时也将网络模型转变为了非线性模型。

2）训练函数选择。训练函数是基于误差来修改权值和阈值的，完成一次训练后继续迭代，直到达到迭代次数或满足精度。采用基于B-R算法模型的训练函数，该算法回归程度较好，预测精度较高。

3）隐藏层节点数选择。隐藏层节点数的确定是算法建立的核心环节，若隐藏层节点数选取过少或过多都会使得训练结果不理想。根据文献得出一些关于隐藏层节点数计算的3个经验公式，见式（6）～（8）

（6）

（7）

m=log2n

（8）

式中m为隐含层节点数；n为输入层节点数；l为输出层节点数；α为（1，10）的常数。

将5组基础数据加上通过多元线性插值法获取的48组数据共53组有效数据作为训练样本，20个指标得分作为样本输入、1个输出指标作为网络输出。

图3中表明，基于B-R算法模型的隐藏层节点数为10时，网络误差达到最低，网络性能此时达到最佳，达到全局最优。

2.2.2 仿真效果分析

1）训练误差变化分析。随着训练模型的迭代次数增加，网络误差越来越小。网络误差的变化趋势如图4所示。

基于B-R算法神经网络模型，当迭代次数为904次时，均方误差达到1.180 5×10-10，此时模型训练截止，模型精度较高，训练次数较多。

2）训练过程回归分析。如图5所示。

图3 隐含层节点数对误差率的影响Fig.3 Effect of the number of hidden layer nodes on the error rate

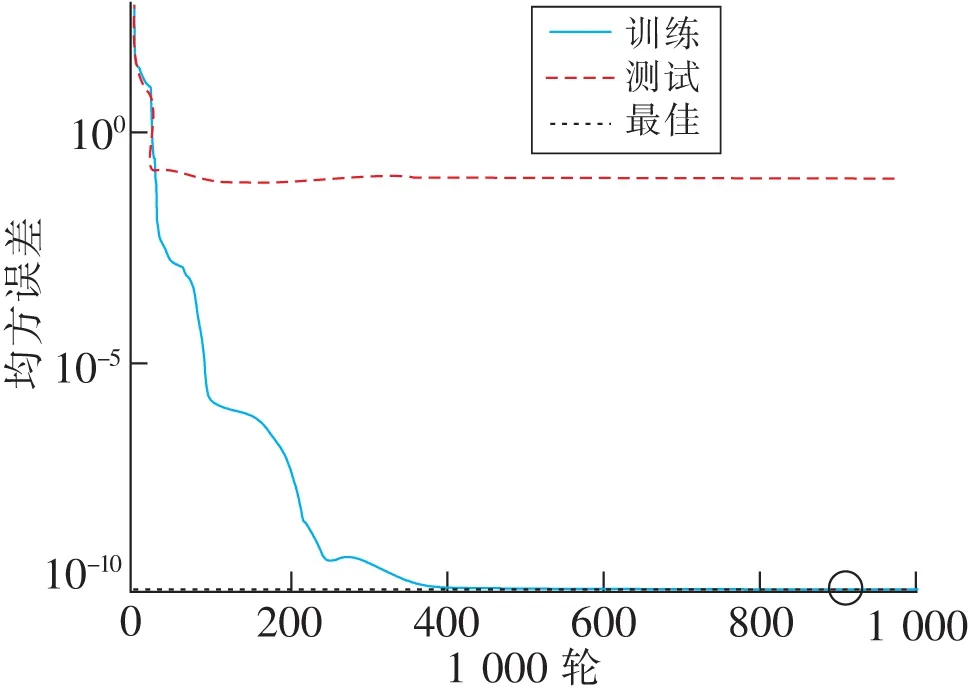
图4 模型训练误差变化Fig.4 Model training error change

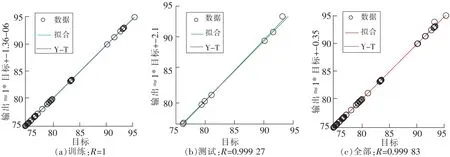
图5 模型训练过程回归状态Fig.5 Regression state of model training process

基于B-R算法的神经网络模型的训练样本相关系数为1，通过分析样本学习训练的结果，对应的2个相关系数值分别对应为：0.999 27（测试样本）和0.999 83（全体样本）。训练样本几乎在一条直线上，训练结果情况较好，此时模型选取的参数和网络性能达到数据归一化后的最佳状态。

3）实际输出与模型输出的仿真结果对比。将5个城市数据和插值48组数据一共53组基础数据输入上述训练好的模型进行模型仿真测试，B-R模型最小误差0.05%，最大误差0.85%，平均误差0.22%，基本达到模型精确的要求，整体仿真结果对比如图6所示。

根据BP神经网络模型仿真分析，发现基于B-R算法的学习训练后的城市安全发展状态BP神经网络评估模型可以较为准确的反映城市安全发展指数与评估指标之间客观而又复杂的非线性关系，即该算法可用于城市安全发展状态评估。随着输入样本学习集数量的增加，BP神经网络评估模型评估结果的准确性会随之增加，误差逐渐减小。

图6 实际输出与模型输出的仿真结果对比Fig.6 Comparison of simulation results between actual output and model output

2.2.3 客观权重计算

建立神经网络算法是为了确定指标的权重，而神经网络训练得到的结果只是各神经网络神经元之间的关系，因此还需对各神经元之间的权重加以分析处理，通过以下指标来描述输入因素和输出因素之间的真实关系。其中绝对影响系数为最终客观权重。

1）相关显著性系数

（9）

x=wki

（10）

2）相关指数

（11）

y=rij

（12）

3）绝对影响系数

（13）

式中i为神经网络输入单元，i=1,2,…,m；j为神经网络输出单元,j=1,2,…,n；k为神经网络的隐含单元，k=1,2,…,p；Wki为输入层层神经元i和隐含层神经元k之间的权系数；wki输出层神经元j和隐含层神经元k之间的权重系数。

2.3 组合权重计算

将指标的主观权重记为w（s）i，客观权重记为w（o）i，2类权重从不同的侧重点反映了各指标的重要性[25]。为确定指标的组合权重，基于距离函数原理对各指标的主观权重和客观权重进行组合，建立二者之间的距离函数，见式（14）

（14）

对主、客观权重进行线性加权，组合得到的组合权重值记为Wf，见式（15）

Wf=αw（s）i+βw（o）i

（15）

式中α,β为2种权重对应的分配系数。

距离函数和分配系数见式（16）

F2（w（s）,w（o））=（α-β）2,α+β=1

（16）

根据公式得出分配系数α=0.483，β=0.517，由此得到综合权重。

3 实例应用

3.1 评估对象选取

根据《GN中国最安全城市评价指标体系》《中国城市公共安全发展报告》等多种城市安全排名结果，选择西安、南京、武汉、北京、石家庄5个上榜的城市作为评估对象，进行纵向横向的对比。

3.2 问卷调查分析

共发放城市安全发展状态评估指标重要度调查问卷20份，回收有效问卷13份，问卷有效率为65%，调查对象的基本信息见表3，从专业技术级别、学历以及工作年限的分布可以看出，该问卷调查数据的质量较高。

表3 调查对象基本信息统计

采用SPSSAU对调查问卷信度进行检验，整体调查问卷的a值为0.938，信度好，可以认为本调查问卷具有较强的稳定性与可靠性。

3.3 指标权重计算

基于网络分析法，结合专家系数，根据式（1）～（5）借助SD软件可计算得到主观权重值；基于BP神经网络算法，进行权重修正，根据式（9）～（13）可计算得到客观权重值；基于主客观权重值，对指标进行组合赋权，根据式（14）～（16）可计算得到综合权重，见表4。

表4 指标综合权重及量化打分

3.4 量化打分

邀请城市安全与应急管理领域专家，根据量化标准对评价指标进行打分作为各指标得分，结果见表4。一级指标权重值中，城市安全源头治理权重值最大，城市安全风险防控和城市安全保障能力权重值接近，符合中国城市安全发展“预防为主”的理念和趋势。

3.5 结果计算与完善建议

将各评估指标的待评城市标准化量化打分与该指标的权重值相乘得到该指标的最后得分，把各基础指标的得分相加，得到待评城市的各子目标层的标准化得分以及城市安全发展状态指数，见表5。城市安全发展状态指数可以从城市安全源头问题、风险防控以及应急救援等全过程全方位综合性体现城市安全发展状态。

表5 指标得分

根据评估模型分析参数变化对评估结果的影响规律，确定等级界限的合理赋值区间，见表6。

表6 城市安全发展状态指数及等级

由此得出5个城市的城市安全发展指数与等级，见表7。

表7 城市安全发展状态指数及等级

综合来看，北京市城市安全发展指数最高，安全发展状态等级等级为Ⅰ级，南京市安全发展状态等级为Ⅱ级，武汉市和石家庄市安全发展状态等级为Ⅲ级，西安市安全发展状态等级为Ⅳ级，结果基本符合实际情况。

其中西安市城市安全源头治理得分较高，说明在城市安全问题的预防工作上成果显著，但是城市安全风险防控、城市安全监督管理和城市安全应急救援3个方面得分较低，建议加强针对城市安全风险的防控设施建设和及时更新检修、加大风险点的辨识和审核、进一步明确政府、企业、个人的安全责任，并提高安全执法效率、加强应急救援队伍和应急避难场所的建设，提高应急联动能力。南京市在城市安全监督管理得分较低，建议加强安全生产安全责任制及考核机制的落实。武汉市在城市安全风险防控、城市安全应急救援2个方面得分较低，建议更新城市禁止产业目录、多开展城市安全风险源辨识评估、进行风险审核并建立联防联控机制，同时加强应急物资储备信息管理系统的建设。北京市整体得分较高，建议进一步加强城市安全风险审核以及应急物资储备信息管理系统的建设。石家庄在城市安全应急救援方面得分较高，但在城市安全风险防控、城市安全监督管理得分较低，建议加强隐患排查力度、增加安全风险防控措施、提高安全执法效率。

4 结 论

1）从源头治理、风险防控、监督管理、保障能力和应急救援5个角度构建城市安全发展状态评估指标体系，采用网络层次分析法、BP神经网络模型计算得到各指标权重值，从而构建城市安全发展状态评估模型，拟合效果较好，真实值和预测值误差较小，因此模型具有较高的准确性和适用性。

2）通过模型得到5个城市安全发展指数，其中北京市城市安全发展指数最高，安全发展状态等级为Ⅰ级，南京市为Ⅱ级，武汉市和石家庄市为Ⅲ级，西安市为Ⅳ级，结果基本符合认知，并依据评估结果，针对不同城市提出加强城市安全发展的建议，应重点在安全风险防控和安全监督管理2个方面开展工作。

3）在该模型中，对于不同地区（如东西部），不同经济情况（如发达城市，欠发达城市），不同城市功能类型（如能源型城市，商业型城市）采取相同的量化方法。为进一步完善模型，需在主客观赋权时按照城市类型对不同城市的指标权重进行差异化处理。