混凝土大坝溃坝动力响应规律数值研究
李旨洪
(江西省水利水电建设集团有限公司,江西 南昌 330025)
1 引言
混凝土坝以混凝土作为坝身材料,其结构简单、施工方便,是一种整体性较好的刚性坝,中、高坝常用这种坝型[1,2]。此外,混凝土坝相对安全可靠,耐久性好,抵抗渗漏、洪水漫溢、地震和战争破坏能力都比较强,广泛用于水利工程中。然而,由于地震等地质作用与材料强度之间的不匹配,混凝土大坝存在潜在的溃坝风险,会导致下游河谷洪水波快速传动,造成严重的财产损失和人员伤亡[3,4]。
当前国内外通过数值模拟和室内试验等手段对混凝土大坝漫顶溃坝进行了相关研究。胡文兵等[5]对该溃决方式进行水动力分析,得到混凝土坝倾倒过程的溃口流量计算公式,并结合概化典型流量过程线法得到了新的溃口流量计算方法;姚霄雯等[6]总结了混凝土坝的溃坝特点,统计了主要溃坝原因,进而提出了混凝土坝的主要溃坝模式及其潜在的溃坝路径;王冰玲等[7]以某一混凝土坝为实例,利用开发的随机网格生成算法建立了大坝模型,对爆炸载荷下混凝土坝的溃坝过程进行了模拟仿真;詹明强等[8]以某一面板堆石坝为工程实例模拟计算了大坝在不同溃决模式下的洪水传播过程,得到了坝下河道沿程典型断面的洪峰流量、最高洪水位及相应的出现时间。此外,还有部分学者通过统计分析、风险评价等方式对混凝土溃坝进行了相关研究[9-15]。
以位于江西省某简化的大坝模型为例,采用计算流体力学CFD程序中的ANSYS FLUENT对其溃坝后的水动力演变过程进行模拟,并对比分析了LES和K-E湍流模型对计算结果的影响,研究成果可为相关工程提供参考。
2 工程概况
大坝位于江西省,是一座以发电为主,兼顾改善城区水环境、航运等综合利用的水利水电工程。坝址以上控制流域面积16546 km2,总库容1.52亿m3,水库正常蓄水位为103.8 m,电站装机容量为32 MW,多年平均发电量13887×106kW·h,85%保证出力5300 kW,装机年利用小时数3528 h。根据《防洪标准》(GB5021-2014)、《水利水电工程等级划分及洪水标准》(SL252-2017)确定该工程属大(2)型,工程等别Ⅱ等。主要建筑物级别为3级,次要建筑物级别为4级,临时建筑物级别为5级,船闸级别为V级。挡水和泄水建筑物设计洪水标准为50 a一遇,校核洪水标准为300 a一遇;消能防冲洪水标准为50 a一遇。厂房非挡水部分设计洪水标准为20 a一遇,校核洪水标准为100 a一遇。大坝电站工程于2011年6月26日动工,主体工程于2011年10月12日正式开工,首台机组(3#机组)于2013年11月12日完成72 h试运行,2014年2月21日全部3台机组完成试运行。工程于2018年4月通过下闸蓄水验收,2020年12月通过竣工验收。
3 数值计算方程
本文通过计算流体力学CFD程序中的ANSYS FLUENT进行模拟。计算采用三维Navier-Stokes方程,并采用LES模型来模拟湍流。LES条件在空间和时间上都是离散的,在本研究中,PISO算法用于解决压力场和速度场之间的转换,使计算以更快的方式收敛。不可压缩液体的质量和力的分离或雷诺平均守恒条件可以单独由下式表达(总控制方程):

式中:uı和uj由流体速度转换而来(m/s);xi和xj为笛卡尔坐标方向;ρ为流体密度(kg/m3);-p为压力平均值(Pa);t为时间(s);u为流体分子黏度(Pa·s);τij为雷诺应力(Pa)。
对总控制方程进行建模后,模拟流体最重要的是对湍流方程进行建模分析。湍流是一种非对称运动,当流体、液体或蒸汽流过坚固表面时,甚至当同一液体的相邻流流过或超过彼此时,湍流都会出现在流体、液体或蒸汽中。目前进行湍流模拟的方法包括大涡模拟法(LES)、分离涡模拟法(DES)、比例-自适应模拟方法(SAS)、雷诺应力(7个方程式)、过渡SST方法、K-Omega湍流模型以及K-Epsilon湍流模型。其中,LES模型和K-Epsilon(以下简称K-E)模型是本文研究的重点。在大涡模拟方法中,先确定了较大的涡,并对较小或亚网格尺度的涡进行建模,从而比一般方法具有更好的稳定性。本研究中,采用了Smagorinsky提出的亚网格尺度模型:

式中:μt是子网格黏度(Pa·s);Slj是更大尺度或定场的应变率,无量纲;δij为张量符号;其余变量含义同上。
涡流黏度建模如下:

式中:Cs为模型参数,取0.1;Δ为过滤器长度刻度(m);ρ为流体密度(kg/m3);为应变率。
K-E模型是计算流体力学(CFD)中最广泛使用的模型,用于模拟湍流条件下的平均流质量。这是一个双条件模型,通过2种传输条件对湍流进行了一般描述。最初传输的变量决定了湍流中的能量,称为湍流动能(k)。第二个传输变量是湍流耗散(ε),决定了湍流动能的扩散速度。对于湍流动能k和湍流耗散ε分别采用下式描述:

式中:C1ϵ和C2ϵ为常量;σk和σϵ分别为k方程和ε方程的湍流Prandtl数;ε为耗散率;k为湍动能;μt是子网格黏度(Pa·s);xi和xj为笛卡尔坐标方向;t为时间(s);ρ为流体密度(kg/m3);Eij表示变形率分量,无量纲。
4 数值模型建立
本文流体力学计算的前期阶段是创建液流区的计算几何条件,Z轴与溃坝流体流动方向有关,X轴与大坝横向有关,Y轴与平行于大坝高度的方向有关。本次建立的模型上游水库长宽2 m、高1 m,下游水库长宽高分别为8、2、0.3 m,其中混凝土密度设置为2400 kg/m3,弹性模量为14 GPa,泊松比为0.2,下游无蓄水,大坝尺寸详见表1,溃坝数值模型如图1所示。数值研究的第二步也是最关键的一步是建立与几何发展相关的网格。Navier-Stokes方程是非线性偏微分方程,将整个流体区域视为一个连续统一体,利用笛卡尔坐标框架,根据区域离散化方法,求解了液流控制方程,即动量条件、连续条件。在有限元法中,通过在适当的空间中加入加权单元来获得数值排列。该技术适用于非结构化网格,采用非结构化网格划分方法分别将流体和坝体划分为3200和2178个网格。完成大坝模型的几何和网格划分后,必须给出边界条件。为了创建实时溃坝模拟,将顶面和下游边界定义为压力出口。此外,水闸不指定任何边界条件,出水口的所有侧面部分全约束。对于顶部自由曲面,大部分采用对称边界条件,并且与无滑移边界条件一样,顶面上既没有对流通量也没有扩散通量。本文计算的监测位置,如图2所示。
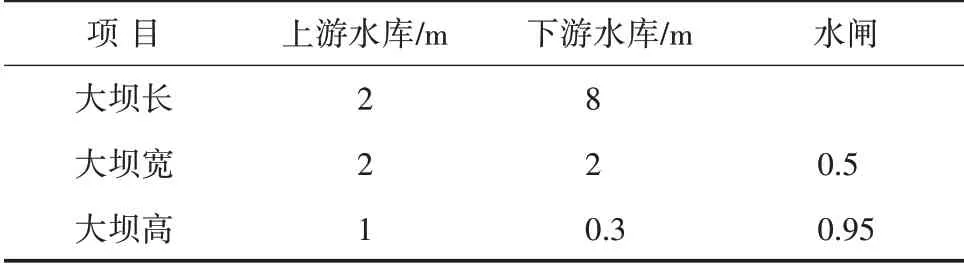
表1 大坝建模尺寸

图1 数值模型

图2 监测点位置
5 数值结果分析
5.1 K-E模型和LES模型计算压力分析
本次的数值结果包括流体速度、水面和底部压力随时间的变化。计算时一旦水从闸门排出,沿下游中轴线扩散,然后在下游端离开。之后,再利用LES模型和K-E模型进行湍流描述。流经闸门的水沿下游中轴线扩散,在水库侧汇合,在下游侧分流,大坝下游的河道面积随着时间的推移而增大。
LES模型和K-E模型计算的不同监测位置的压力如图3所示,如A、B、C、D、E、F、G,并给出其随时间变化的规律。上游水库位置(如位置A和位置B)的底部压力最初为1 m水深的压力,随着时间增加,压力会缓慢降低。在时间t=0时,闸门位置C和位置G附近没有压力,模拟开始后,底部压力突然增加,并瞬时达到峰值。随着时间的进一步增加,水在下游扩散并到达下游区域的终点,底部压力降低。沿着下游的位置E和F的压力变化,如图4所示。由图4可知,下游位置的底部压力变化与C点和G点相似,在一段时间后达到峰值,此外闸门开启和压力增加之间具有一定时间差,闸门开启位置附近的峰值压力明显高于下游位置。
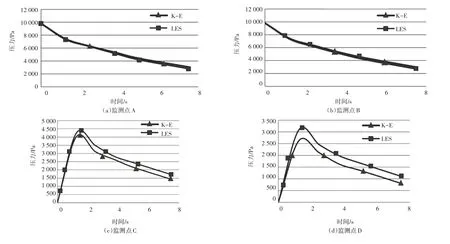
图3 LES模型和K-E模型计算的不同监测位置的压力
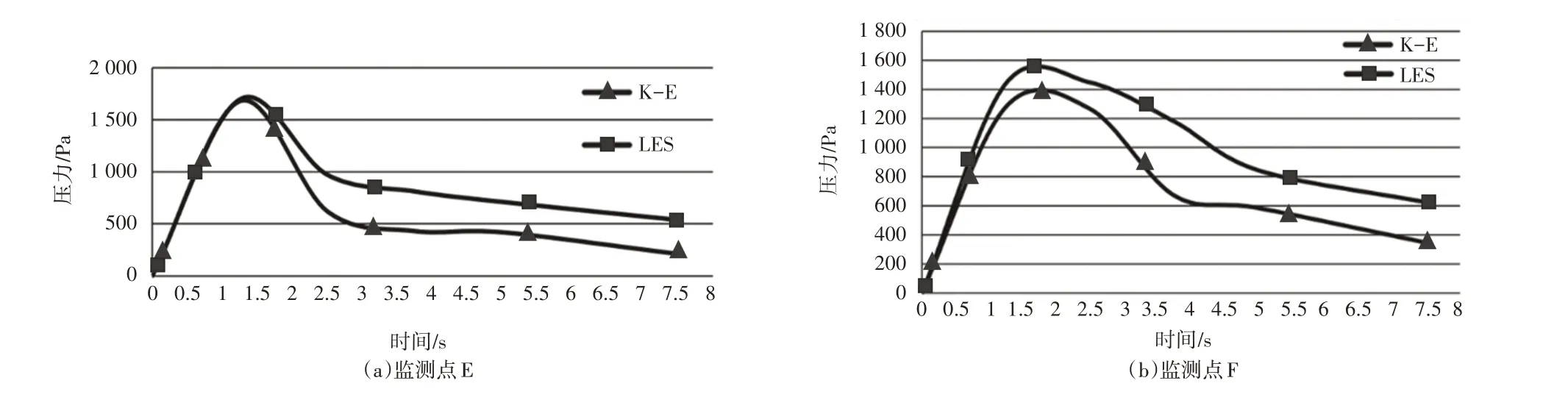
图4 下游位置的压力变化
5.2 K-E模型和LES模型计算流速分析
监测点平均速度随时间的变化规律如图5所示,使用LES和K-E模型在上游位置(如A和B)进行速度计算,并相互比较。由图5可知,上游侧流速随时间增加,在溃坝模拟后近2.5 s达到峰值,之后随着时间的增加而进一步降低,并保持接近恒定值。然而,在闸门位置,速度在短时间内达到峰值,并缓慢下降。对于下游速度,闸门打开和速度增加之间存在时间滞后。在位置F处,速度几乎为零,直到时间t=2 s,然后缓慢增加;时间t=5 s后,流速保持不变,因为大坝上游和下游的水位相同。此外,本文还计算了沿大坝长度的速度变化。

图5 监测点平均速度随时间的变化规律
计算结果表明,水波的速度在决口后立即沿长度增加,在涌浪后随距离减少。在大坝闸门周围,由于决口,流速很高,渠道的特性允许水流扩散到一个宽的横截面,从而使流速沿水流方向降低。运行时观察到的监测点流速在1.25和2.5 s左右大致接近,但随着运行时间增加到3.5 s,产生的速度会低于之前。这主要是由于溃坝后上游储水量减少以及下游横截面增加。
6 结论
本文以位于江西省某简化的大坝模型为例,采用计算流体力学CFD程序中的ANSYS FLUENT对其溃坝后的水动力演变过程进行模拟,并对比分析了LES和K-E湍流模型对计算结果的影响。结果表明,用LES和K-E湍流模型预测的速度剖面显示出显著差异,尤其是在大坝下游开口附近。然而,使用LES和K-E湍流模型预测的底部压力在上游区域监测点表现出相似性,但在下游监测点出现了显著的变化。最后,水波的速度在决口后立即沿长度增加,在涌浪后随距离减少,研究成果可为相关工程提供参考。

