基于NOMA的F-RAN下的无线资源分配优化
林志坚,张清松,陈平平
(福州大学物理与信息工程学院,福建福州350108)
为了解决云无线接入网(cloud radio access networks,C-RAN)受限于前传链路,以及云中心上计算卸载所带来的传输时延问题[1],雾无线接入网(fog radio access networks,F-RAN)的架构被提出[2].具体地,通过将云中心的部分存储、计算功能下移到网络的边缘,将现有的射频拉远头(remote radio head,RRH)升级成同时具有计算、存储、信号处理和资源管理的雾节点(fog access point,F-AP),使得用户可以不必通过前传链路向基带池获取服务,能够从更靠近用户的F-AP上获得更及时的响应[3].
另一方面,非正交多址(non-orthogonal multiple access,NOMA)作为传统正交多址接入(orthogonal multiple access,OMA)技术的改进方案被提出[4].NOMA允许多个用户使用同一时频资源块进行传输,并在接收端通过串行干扰消除技术来逐一获取目标用户信号.与OMA相比,NOMA在频谱效率、时延性能方面有较大的性能增益[5].
基于NOMA能够将多个用户的计算任务同时卸载给同个F-AP的特点,已经有相关研究利用NOMA来改善F-RAN的卸载性能.具体来说,Liu等[6]考虑存在不同F-AP复用同一资源块(resource block,RB)的情况,通过联合优化无线资源和计算资源的分配,以实现最大化卸载能源效率.郝万明等[7]通过优化NOMA功率分配和任务卸载决策,实现了多用户单F-AP场景下的能耗最小化,同时确保了用户的保密传输和时延约束需求.张海波等[8]基于混合NOMA传输的卸载策略,提出一种基于深度学习网络的博弈算法进行信道选择和功率分配,有效减少多了用户卸载的时延和能耗.Wen等[9]假设F-AP之间占用独立的正交子信道且每个F-AP采用NOMA为用户提供通信服务,并对能源效率最大化目标下的资源分配进行了研究.Liu等[10]对一个通用的多F-AP多用户,且用户任务可以选择在F-AP上或是云中心上进行卸载的系统进行研究,通过联合优化卸载决策、用户调度和资源分配实现了最小化系统总能量成本和用户延迟开销.Rai等[11]对前传链路容量限制的情况进行传输模式优化和功率分配,得到了最大化的用户通信速率.
在现有的基于NOMA的F-RAN研究中,文献[6-8]没有考虑云中心强大的计算能力,只将F-AP作为卸载节点,而文献[9-11]虽然将F-AP和云中心作为卸载节点,但没有将RRH作为云计算卸载的中继节点.在未来5G通信场景中,RRH向F-AP的升级过渡并非一蹴而就,将出现大量RRH和F-AP并存的情况,因此同时考虑F-AP和RRH进行研究具有实际意义.
根据作者观察,目前只有少数研究考虑RRH和F-AP并存的场景.Liu等[12]研究了具有多个F-AP和RRH的F-RAN场景下的资源分配问题,其优化目标是最大化用户的通信速率,但该文献忽视了用户任务和F-AP计算能力的异构情况,且未考虑云中心参与通信的情况.Ma等[13]对卸载时延和通信速率进行优化,但采用OMA进行传输,且未考虑RB不足的情况.因此,与上述文献不同,本研究提出了一种新型的基于NOMA的F-RAN卸载方案,通过优化F-AP与RRH之间的资源分配和用户的发射功率以实现最小化的用户最大卸载时延.本文的贡献包括以下几个方面:
1) 本文提出了一种新型的基于NOMA的F-RAN卸载方案,并同时考虑了共层干扰和跨层干扰,通过对资源块的分配和用户发射功率的优化实现最小化用户的最大卸载时延.
2) 本文将优化问题解耦成RB分配问题和用户的发射功率分配问题.将F-AP与RRH之间的RB分配问题转换成图论中的超图问题,并通过基于超图的匹配算法进行求解.对于非凸的功率优化问题,采用了序列二次规划(sequential quadratic programing,SQP)方法来求解用户的发射功率.
1 系统模型
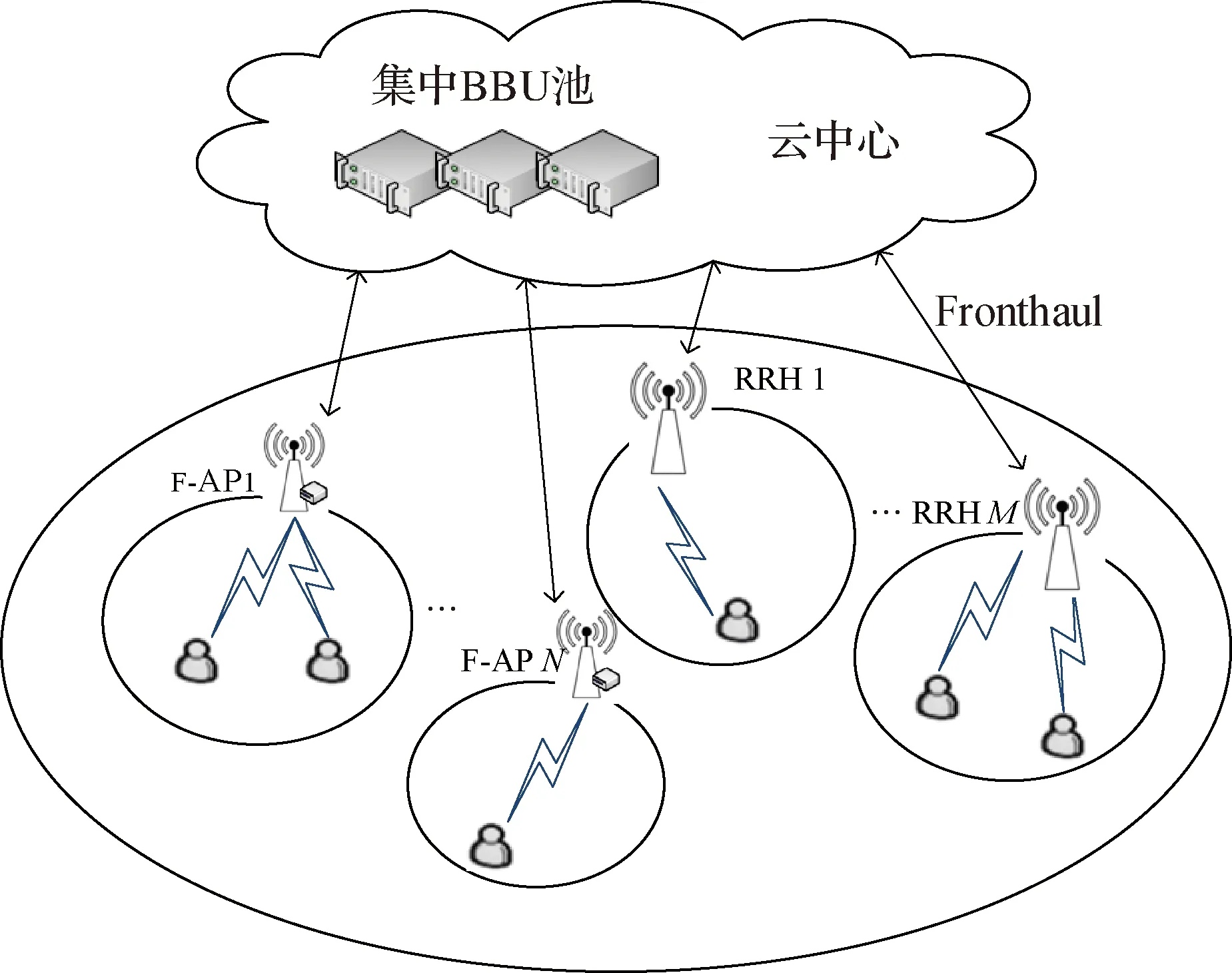
图1 系统模型Fig.1System model

1.1 通信模型


(1)
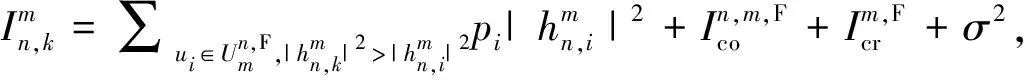
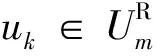
(2)
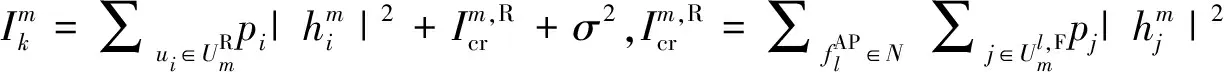

(3)
(4)
1.2 计算模型
对于与F-AP关联的用户,可以选择在F-AP上进行卸载或是通过前传链路将任务卸载到云中心上计算.对于与RRH关联的用户,由于RRH本身不具备计算能力,只能转发到云中心上进行计算卸载.与大多数研究[15-16]类似,由于计算结果较小,本文忽略结果返回的过程.
1) F-AP计算:对于在F-AP上计算的任务,同文献[17]一样,假设F-AP按照每个用户的计算任务大小占其总计算任务大小的比例分配计算资源,从而免去计算资源的分配,这不在本文的优化范围之内.此时在同一F-AP上进行计算卸载的用户任务具有相同的计算时间,在F-APn上进行计算卸载的用户k的计算时间表示为:
(5)
其中,fn表示F-APn的计算能力.
2) 云计算:对于在云中心上计算的任务,需要通过前传链路将计算任务从关联的F-AP或RRH传输到云中心上.考虑到云中心的计算资源足够,为每个任务分配了固定的计算资源fc.因此,在云上计算的uk需要同时考虑额外的通信时延消耗和计算时延,云卸载的计算时间表示为:
(6)
其中,Re为前传速率.


2 问题阐述

(7)
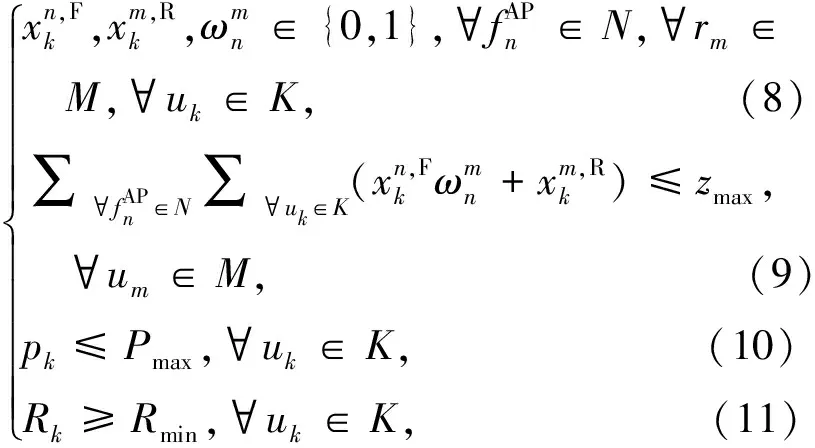
其中,约束式(8)表示用户关联系数和RB分配系数为二进制变量;约束式(9)表示访问同一子信道的用户设备数量不超过zmax,这是为了抑制F-AP之间的同层干扰和F-AP与RRH之间的共层干扰;约束式(10)表示用户的发射功率不能大于最大发射功率Pmax;约束式(11)表示用户uk到F-AP、RRH的通信速率Rk需大于最小通信速率Rmin.
3 优化方法

3.1 RB分配优化
在假设用户的发射功率已知的情况下,利用基于超图的匹配算法对F-AP的RB分配进行优化.设G=(V,ε)为一个加权的无向超图,其中V为顶点集,顶点包括两种类型,一种顶点代表RB(RRH),另一种顶点代表F-AP节点,表示为sv,为了便于分辨,给代表不同F-AP的顶点着不同的颜色,F-AP顶点集定义为V′,RB顶点不着色,ε为超边集合.与顶点v相关联的边数称为顶点v的度,记为d(v).在满足约束式(9)和(11)的前提下,当某个RBm能被一个或多个F-AP复用时,RBm与这些F-AP顶点形成一条超边,表示RBm的一种复用情况.超边权重设置为复用该RB的所有用户的最大时延.至此,F-AP与RB的关联问题可以转化成图G的匹配问题.
定义1在一张图G=(V,ε)中,强删除一个顶点v∈V意味着从ε中删除所有包括该顶点v的边,并且将v移除V.
基于强删除的特点和文献[19]的启发,本研究提出了一种基于超图的匹配算法来解决F-AP与RB的关联问题.具体步骤如算法1所示,将超图G中的边按照权重大小排列,依此删除权重最大的边,直到出现一个F-AP顶点sv只与一条边e关联,此时e则为一种确定的F-AP与RB的关联情况.从图G中对e中的所有顶点进行强删除操作,之后继续依此删除权重最大的边,按照以上原则寻找新的F-AP顶点sv和超边e,直到图中所有的F-AP顶点都被删除.根据最终剩余的边{ej},可以从各条边所包含的顶点映射出F-AP与RB的关联关系ω.
算法1基于超图的RB分配算法
1. 初始化:根据约束式(9)和(11)构造图G=(V,ε),初始化i=1,并将ε按降序排列得到εsort
2. whileV′≠∅ do
3. if ∃d(sv)=1,sv∈V′ then
4. 找出sv此时所属的超边e,ei←e,i=i+1,对e中的所有顶点执行强删除操作
5. else
6. 删除目前εsort中权重最大的超边
7. end if
8. end while
9. 输出{ej},j=1,2,…,i-1
3.2 发射功率优化
由于每个RB之间是正交的,它们的传输互不干扰,因此在已知RB分配的情况下,对整个系统的发射功率优化问题可以简化为单个RBm下的最小化最大时延问题:
(12)

由于式(12)中的min-max优化问题难以通过一般的优化方法求解,引入一个辅助变量y,问题(12)可以转变为
miny,
(16)
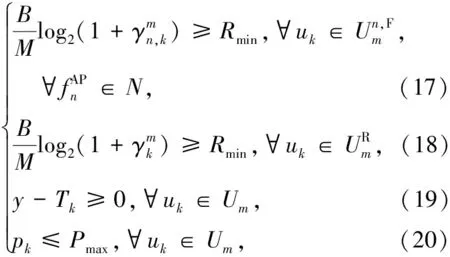
其中,根据uk已知的关联情况和计算卸载方式而定.由于受到其他用户信号的干扰,约束式(17)~(20)为非凸约束,难以通过常用的非凸优化方法求解,因此本文基于SQP方法[20],对用户的发射功率进行优化.为简化优化过程,本文对约束式(17)~(20)进行变换,如下所示:
(21)
(22)

l(p)=[rmin(p)T,Y(p)T,pmax(p)T],
(23)
其中
rmin(p)=[Rmin-R1, …,Rmin-Rk]T,
(24)
Y(p)=[T1-y, …,Tk-y]T,
(25)
pmax(p)=[p1-Pmax,…,pk-Pmax]T,
(26)

(27)
(28)
(29)
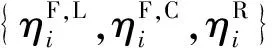
(30)
其中,λ、β、ψ均为拉格朗日乘子.

K(p,λ,β,ψ)s=
[(gL(p(k)))T,(rmin(p(k)))T,(Y(pk))T
(pmax(p(k)))T]T,
(31)
其中,gL(p(k))表示第k次迭代的L(p)的梯度,此时可以利用校正矩阵s在第k轮迭代中更新(p,λ,β,ψ),如下所示:
(32)
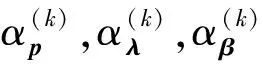
算法2基于SQP的发射功率优化算法
1. 初始化:给定初始(p(0),λ(0),β(0),ψ(0)),K(p(0),λ(0),β(0),ψ(0)),gL(p(0)),rmin(p(0)),Y(p(0)),pmax(p(0))以及一个充分小的正实数ξ,令t=1,tmax为最大迭代次数
2. 通过式(31)更新校正向量s,并通过公式(32)更新得到(p(1),λ(1),β(1),ψ(1))
3. while ‖(p(t),λ(t),β(t),ψ(t))-(p(t-1),λ(t-1),β(t-1),ψ(t-1))‖>ξ且t 4. 通过式(31)更新校正向量s,并通过式(32)更新得到(p(t+1),λ(t+1),β(t+1),ψ(t+1)) 5. end while 6. 输出发射功率p(t)及对应的最大时延y=max{(Tk)(t)},∀uk∈Um 算法3联合的资源分配算法 1. 初始化:给定初始化的用户发射功率p(0),迭代次数j=1和一个充分小的正实数ξ 2. while ‖y(ω(j),p(j))-y(ω(j-1),p(j-1))‖>ξdo 3. 根据已知的发射功率,利用算法1更新RB分配方案ω(j) 4. 根据求得的RB分配方案,利用算法2更新用户发射功率p(j) 5.j=j+1 6. end while 7. 输出最大时延y(ω(j),p(j))=max{(Tk)},∀uk∈Um 定理1算法3在每轮迭代中减少用户的最大时延,并经过有限的迭代次数后达到收敛. 证明 经过第j轮迭代优化后,得到一个解(ω(j),p(j)).在第j+1轮迭代中,在固定用户发射功率p(j)的情况下,利用算法1求得一个优化解y(ω(j+1),p(j))≤y(ω(j),p(j)),类似地,在固定RB分配ω(j+1)后,利用算法2求得一个新的解y(ω(j+1),p(j+1))≤y(ω(j+1),p(j)).因此y(ω(j+1),p(j+1))≤y(ω(j),p(j))成立,即算法3在每轮迭代中减小用户的最大时延.由于用户的最大时延是一个有下界的值,因此算法3会在有限的迭代次数内达到收敛. 在本节中,通过仿真验证了所提卸载方案和所提算法的有效性.假设系统总带宽为5 MHz,路径损耗指数为4,用户的发射功率为26 dBm,任务大小在[100,1 000] kB区间,计算密度为1 000 cycle/bit,F-AP的计算能力在[3,5] GHz区间,云提供给每个用户的计算资源为10 GHz,前传速率设置为10 Mbit/s. 图2 随着RB数量的增多,有效系统容量的变化Fig.2With the increase of the number of RBs, the change of effective system capacity 在图2中,比较了不同zmax下系统的有效系统容量[18],其中有效系统容量的定义为计算任务被成功处理的用户总数.用户数量设置为40,从图中可知,起初RB数量不足,导致有效系统容量都比较低,随着RB数量的增多,能够得到计算处理的用户任务数量增多,并最终达到稳定.此外,在RB数量不足时,zmax更大表示能够容纳的用户设备数量更多,因此有效系统容量也会更高. 在图3中,比较在不同RB数量下,随着用户数量的增多,用户最大时延的变化,其中zmax=3.从图3可以看出,随着用户数量的增多,用户最大时延逐渐上升,这是因为RB的复用情况变得更为普遍,用户受到的干扰增大导致传输时延增大.另外可以注意到,在RB数量更多的情况下,系统最大时延反而上升,这是因为系统的总带宽是被每个RB平分的,在RB复用情况不严重时,RB数量的增多不能明显减少RB复用情况,反而它所导致的用户传输带宽减少会使用户最大时延增大. 图3 随着用户数量的增多,不同RB数量下用户最大时延的变化Fig.3With the increase of the number of users, the change of maximum delay under different number of RBs 图4展示了所提出的卸载方案在时延性能上的优越性.将本文卸载方案与F-AP只作为中继节点、以及F-AP只提供计算功能不提供中继转发功能的两种卸载方案进行比较,从图4可以看出,由于本文卸载方案能够为用户提供更加灵活的计算卸载,因此能获得更低的时延性能.另外还观察到在F-AP只作为中继节点方案中,前传速率增大时,能够获得更低的时延,这是因为此时云计算卸载的传输时延变短.除此之外还能观察到,当用户数量增多时,F-AP只提供计算功能与其他方案的时延性能差距逐渐拉大,这是因为每个用户能分配得到的F-AP的计算资源变少.此外,本文算法的时延平均仅比通过穷尽搜索法得到的最优解高3.86%,这也验证了本文所提算法的有效性. 图4 随着用户数量的增多,不同卸载方案下用户最大时延的变化Fig.4With the increase of the number of users, the change of maximum delay under different offloading scheme 本文提出一个基于NOMA的F-RAN下的计算卸载方案,用户任务可以在F-AP上进行计算卸载,也可以通过F-AP、RRH转发到云中心上进行计算卸载,并考虑在RB数量不足的情况下,多个F-AP可以共用同一个RB以提高频谱效率.本文针对用户受到的最大时延,研究了所提卸载方案下的资源分配问题,为了有效地解决优化问题,对其进行解耦,首先将RB分配问题转化为超图的匹配问题进行求解,其次利用SQP算法解决了非凸的发射功率优化问题,最后基于上述两算法进行迭代,提出了联合的资源分配方案.仿真结果证明了该卸载方案能充分的利用RRH和F-AP资源,仅比穷尽搜索法得到的最优解的时延高3.86%,可广泛用于4G到5G的过渡阶段.3.3 联合资源分配算法
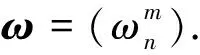

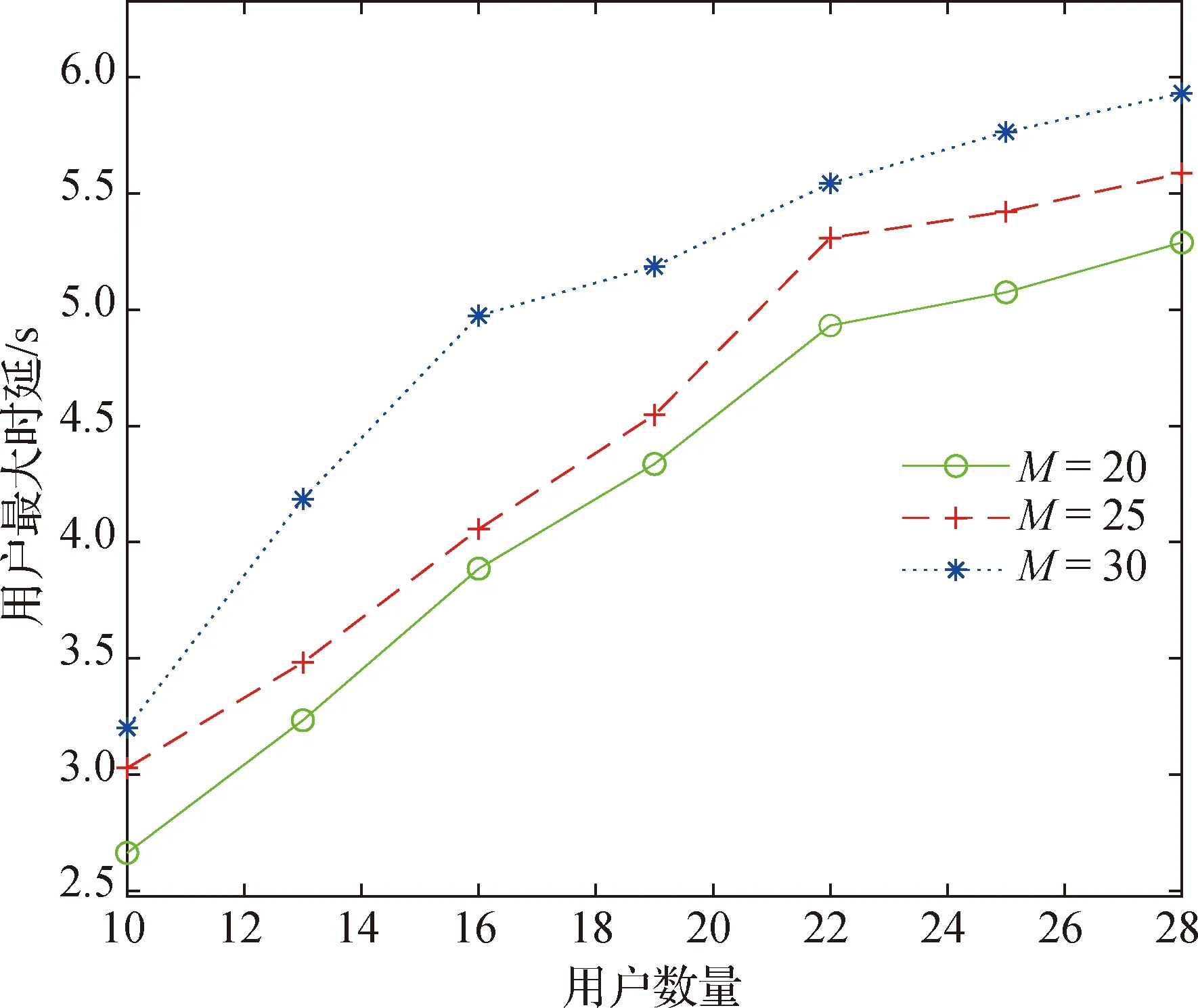
4 仿真结果及分析

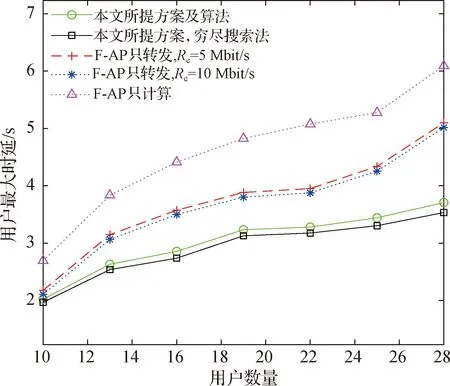
5 结 论

