月球捕获制动和远程交会一体化制导算法
王高阳,胡海霞*,解永春
(1.北京控制工程研究所,北京100190;2.空间智能控制技术重点实验室,北京100190)
近年来,载人登月作为载人航天的热点方向之一,得到了美、俄、欧洲等地的普遍关注[1],他们都提出了自己的方案,如美国Artemis计划的登月方案是通过位于月球轨道的门户,采用可重复利用的月球着陆器,使航天员往返于月球表面[2].彭祺擘等[3]对载人登月的飞行方案进行研究,归纳总结出4种登月飞行方案,其中基于环月轨道的两次发射一次组装的登月方案能够降低对运载的要求,但是如何实现载人飞船与飞行在环月圆轨道的登月舱的交会对接是此方案的关键问题.
载人飞船由地球出发,到达月球后需进行减速制动,以完成月球捕获.王宏等[4]和李革非等[5]在“嫦娥”一号背景下,在第一近月点的位置上对第一次月球捕获制动时所需的脉冲速度增量进行分析,通过仿真计算指出最小速度增量为200 m/s时,可基本实现月球捕获.载人飞船进行月球捕获制动时,登月舱运行在轨道高度更低的环月圆轨道上,理论上,此时两者相位差存在0°~360°的不确定性.由于载人登月任务对任务时间周期和燃料都有严格要求,载人飞船必须具备在特定时间内、以最少的速度增量完成捕获制动和远程交会的能力.
月球轨道快速交会的研究多是从月面起飞的快速交会,如 Apollo 11~12采用基于霍曼变轨的共椭圆交会方案,Apollo 14之后采用基于Lambert变轨的直接交会方案[6-7].对于共面圆轨道,不考虑时间约束的情况下,平面内的最优交会的解是双脉冲霍曼变轨,但是霍曼变轨需要特定的初始相位,要实现全相位交会,需要消耗更多时间.Lambert变轨不仅适用于共面圆轨道,还适用于非共面椭圆轨道.在给定转移时间后,只需追踪器的初末位置,即可求出变轨所需要的两次脉冲.但是这两次脉冲的大小与追踪器和目标器的初始相位角和转移时间密切相关,容易遇到高能耗区.如轨道高度约275 km的追踪器以某固定相位差交会轨道高度200 km的目标器,2个轨道周期内的不同转移时间对应所需的速度增量从100 m/s到4 000 m/s 不等.
目前,最优多脉冲轨道交会问题的求解优化算法有以梯度法为代表的经典优化算法和以遗传算法为代表的智能算法.经典优化算法在解决传统优化问题时能起到较好的效果,但随着优化问题规模和复杂程度的不断增大,经典优化算法逐渐凸显出其局限性[8].智能算法以其较强的适用性和鲁棒性,在一些大型、复杂非线性系统的求解中具有独特的优势,在飞行器轨迹优化设计领域已有成功的应用[9].Mian等[10]应用多种最新的进化算法求解多脉冲最优交会问题,并对其进行比较.虽然智能算法在全局搜索性等方面有独特的优势,但是局部搜索能力不如经典优化算法,智能算法与经典优化算法混合使用是一个新的研究方向.Luo等[11]采用了混合遗传算法和Clohessy-Wiltshire(C-W)方程,研究比较了近地轨道多脉冲最优交会的问题.刘东兴等[12]利用混合算法和C-W方程,对在轨服务航天器进行轨道路径规划,求解出一条服务航天器到目标航天器的最优机动轨道路径.但是,航天器远程交会时的距离较远,使用C-W制导误差大,采用基于绝对定轨的轨控策略设计远程交会方案更加适合[13].
本文针对我国未来载人登月任务中载人飞船在月球捕获制动后与登月舱快速交会的需求,研究在指定时间和任意初始相位角的前提下,飞船实现月球捕获制动和远程交会一体化的最优多脉冲轨道转移问题.基于Lambert变轨,综合考虑终端条件、捕获制动和远程交会的时间、最大速度增量等约束条件,设计了多脉冲捕获制动和远程交会一体化制导的规划模型.同时兼顾遗传算法的全局搜索能力和经典优化算法的局部搜索能力,设计了一种串行混合遗传算法,使得求解结果更加优越.通过仿真验证和对比分析,证明混合遗传算法在提高求解质量方面的优越性.
1 月球捕获制动和远程交会一体化制导规划模型
1.1 捕获制动和远程交会轨道转移数学模型
飞船经地月转移到达月球,地月转移轨道相对于月球为双曲线轨道,飞船飞至近月点时必须进行减速制动以被月球引力捕获,否则飞船会飞离地月系统不会返回[14].图1是捕获制动和多脉冲远程交会示意图,初始时刻,飞船作为追踪器位于近月点C0点,登月舱作为目标器位于环月圆轨道的T0点,飞船与登月舱之间的初始相位角差为θ0.飞船在C0点施加月球捕获制动脉冲,在C1、C2、Cf点施加远程交会脉冲,经过一体化制导,最终到达高于登月舱轨道高度h、相位领先登月舱θ1的指定位置(图中Cf点).在整个过程中,总时间tq1+tq2+tq3=Tq可根据时间约束来确定,通过在初始位置C0和终点位置Cf之间增加或减少脉冲来研究最优多脉冲一体化制导的问题.

图1 月球捕获制动和远程交会Fig.1Lunar capture and far-range rendezvous
假设航天器在轨道机动的过程中满足中心反平方引力场假设,则轨道动力学方程为:
(1)
其中:r是航天器的位置矢量,v是航天器的速度矢量,μm是月球的引力常数.
设飞船在远程交会的过程中采用N(N≥2)次脉冲,飞船初始的位置、速度和时刻分别用r0、v0和t0表示,飞船终端的位置、速度和时刻分别用rf、vf和tf来表示.脉冲施加前和脉冲施加后分别用上标“-”和 “+”表示,则:
(2)
其中:n(1≤n≤N)表示远程交会过程的第n次脉冲,tn表示第n次脉冲的作用时刻.
依据文献[15],令

(3)
是方程(1)的解,则第n次脉冲满足:
(4)
远程交会过程的第1次脉冲作用前满足:
(5)

远程交会过程的第N次脉冲作用后满足:

1.2 优化问题描述
如图2所示,给定航天器在轨道上P1、P2两点的位置矢量r1、r2,转移时间Δt和运动方向,可以利用Lambert方法求解P1、P2两点的速度.通过推导,可以得出如下Lambert方程:
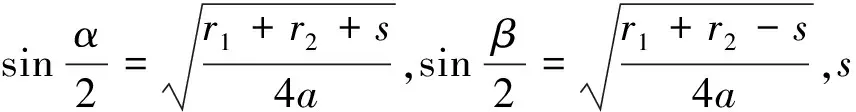

图2 Lambert方法示意图Fig.2Sketch map of Lambert method
在月球捕获制动中多使用切向脉冲,本文以远程交会脉冲的作用时刻ti和脉冲矢量Δvi作为优化变量.为了确保规划模型解的有效性,最后两次脉冲利用Lambert方法求解,即:
其中:Lambert(rN-1,rN,tN-tN-1)是关于rN-1、rN和tN-tN-1的Lambert方程,本文根据文献[15-17]的普适量法进行求解.
综上,一体化制导规划模型的优化变量可表示为:
x=(t1,t2,…,tN-1,Δv0,Δv1,Δv2,…,ΔvN-2),
(6)
其中:Δv0是捕获制动的脉冲大小,Δvi=(Δvix,Δviy,Δviz),因此x是4N-6维向量.
一体化制导的轨道转移问题可以描述为对式(6)进行优化,使一体化制导所需总的脉冲最小,即:
脉冲施加时刻满足的约束条件为:
t0 (7) 考虑到实际要求,例如脉冲机动前需要进行调姿,两次脉冲之间要预留一定的时间间隔,即满足如下约束: ti+1-ti≥ΔTmax(i=0,1,…,N-1). (8) 脉冲约束要考虑到捕获制动的成功性、最大脉冲限制的约束,根据文献[5],捕获制动脉冲不能太小,否则会捕获失败,但是也不能太大,要考虑到发动机的限制,因此捕获制动脉冲的约束为: Δvmin≤Δv0≤Δvmax. (9) 远程交会过程中脉冲的约束主要受限于发动机的限制,即: |Δvn|≤Δvmax. (10) 在远程交会的终点,飞船和登月舱的相对位置和相对速度需达到终点要求,为飞船的近程交会创造条件.在登月舱的轨道坐标系下,飞船在制导末端的相对位置和相对速度需满足: (11) 由上述可见,月球捕获制动和远程交会一体化制导问题以燃料(速度增量)为性能指标,且脉冲大小和间隔、转移时间、终端状态等都受约束.这种轨道机动优化问题可以基于不同数值方法求解,本文采用的是基于遗传算法和单纯形算法的混合遗传算法. 遗传算法具有较强的全局搜索能力,但是在局部搜索能力和计算速度方面较差.单纯形算法局部搜索能力强,但是对初始值敏感,容易陷入到局部极小.因此,为了提高求解质量,本文使用一种串行混合遗传算法对一体化制导律进行优化设计,即首先利用遗传算法进行全局优化,然后利用单纯形算法进行局部优化,进而得到最终解. 遗传算法是一种借鉴生物界“适者生存”的自然选择和自然遗传机制思想的随机搜索算法[18],算法中的每一个可能解被编码成一个“染色体”,即个体,若干个体组成一个种群.算法开始时,种群内的个体根据解的可行域随机产生,然后根据适应度函数计算得到每一个个体的适应度值,通过适应度值的高低对个体进行选择,保留优秀的个体,淘汰坏的个体.保留下的个体经过交叉、变异操作形成下一代个体,由于新一代个体保留上一代个体的优良性状,因此性能优于上一代,这样会朝着最优解的方向进化.利用遗传算法对一体化制导律的全局优化设计如下. 1) 染色体编码 本文采用实数编码的方式,实数编码可以方便地表示大范围的数,扩大搜索空间,也能够降低算法的复杂性,提高计算效率.一体化制导规划模型的优化变量x经过编码可表示为: x=(x1,x2,…,x4N-6). 2) 适应度函数 由于单纯形算法和遗传算法只能求解无约束问题,本文采用罚函数法处理约束条件,把有约束问题转化为无约束问题进行求解. (12) 其中:M是惩罚因子,gi(x)≤0是式(7)~(11)的约束条件. 适应度函数是衡量个体好坏的重要标准,它是由目标函数转换而来.一般而言,适应度函数值越大,个体性能越好.本文一体化制导规划模型要最小化总的脉冲大小,因此需要对式(12)进行转换,本文的适应度函数如下: 3) 算子操作 (i) 选择 选择是从旧种群中以一定概率选择一些优良个体,保留到下一代种群,被选中的概率与个体的适应度值有关,适应度值越大,被选中的概率越大.本文采用轮盘赌法进行选择操作,优化变量xi被选中的概率为: 其中P为种群中个体的数量. (ii) 交叉 交叉是通过随机选择种群中两个个体进行交换组合,产生新的个体.优化变量xi和xj在第l位的交叉公式为: (xil=rxil+(1-r)xjl, 就苏珊·桑塔格后期的美学思想而言,更多的是对艺术作品与生活关系的思考。艺术可能导致生活中的方方面面都有幸成为这个庞大体系中的一个微小的部分,这种将艺术生活化、生活审美化是苏珊·桑塔格后期美学思想的一个突出特点。 xjl=rxjl+(1-r)xil,) 其中r是[0,1]之间的随机数. (iii) 变异 变异是以一定概率选择某些个体,选择其中的某一点进行变异以产生新个体.优化变量xi在第l位的变异公式为: 式中:Umax和Umin分别是xil定义域的上下界;T(g)=r2(1-g/Gmax)b,r1r2是区间[0,1]之间的随机数,g是当前迭代次数,Gmax是最大迭代次数,b是非均匀算子,这里取为2. 单纯形算法作为经典优化算法之一,通过函数值计算的方式寻找函数的最小值,计算简单,速度快,局部收敛性强.单纯形算法通过反射、压缩和扩张的操作实现对函数最小值的求解[19].由式(6)可知,优化变量x的维数为4N-6.首先根据初始优化变量x0生成与其有相同维数的4N-6个变量x1,x2,…,x4N-6,然后利用单纯形法对一体化制导律进行局部优化,操作如下. Step2 对xh进行反射操作得到变量xr,函数值为Fr,如果Fr Step3 如果Fe Step5 如果Fr>Fh,对xr进行收缩操作得到变量xc;否则,用xr替换xh,然后再进行收缩操作. Step6 如果Fc>Fh,对所有变量进行缩小,转Step7;否则,用xc替换xh,转Step7. Step7 计算所有变量函数值的标准差,判断上一次迭代和本次迭代的标准差变化是否满足终止条件,若满足,终止循环,否则转Step1. 综上,一体化制导律的局部优化流程图如图3所示. 图3 一体化制导律的局部优化流程图Fig.3Local optimization flow chart of integrated guidance 本文一体化制导律的整体优化设计如图4所示.首先采用2.1的全局优化方法对一体化制导规划模型的解进行全局寻优,以算法的最大进化代数作为终止条件,达到条件后得到初步解,然后根据此解产生初始变量,采用2.2的局部优化方法进行迭代,以满足终止条件后得到的解作为最优解. 图4 一体化制导律的优化设计图Fig.4Optimal design of the integrated guidance 1) 仿真参数 初始时刻,登月舱位于轨道倾角为28.5°,轨道高度为200 km的环月圆轨道,载人飞船经过地月转移到达轨道高度为250 km的近月点,假设此时登月舱的相位角领先飞船210°.在月球惯性系下,飞船的初始状态向量为: rchaser0=(1 987.4 km,0.0 km,0.0 km), vchaser0=(0.0 km/s,1.95 km/s,1.06 km/s). 飞船经过捕获制动和快速远程交会,到达登月舱前上方、相距约51 km的终点位置,在登月舱轨道坐标系内的相对位置和相对速度为: rrelative=(50.0 km,0.0 km,-10.0 km), vrelative=(-12.3 m/s,0.0 m/s,0.0 m/s). 月球捕获制动所需的最小速度增量约束为300 m/s,最大速度增量约束为900 m/s,相邻两次脉冲之间的时间间隔约束为200 s. 2) 固定时间下一体化制导算法比较 为了验证本文算法的有效性和优越性,以四脉冲为例,比较单纯形算法、遗传算法和混合遗传算法对捕获制动和远程交会一体化制导的求解结果.考虑到遗传算法的随机性,对每种算法独立运行20次,初始种群规模为400,交叉概率0.92,变异概率0.10,遗传算法和混合遗传算法的最大进化代数均为160代,一体化制导的时间设定为5 h.各算法总的速度增量统计如表1所示. 表1 速度增量统计结果 图5是混合遗传算法最优解的迭代过程图,图6是利用混合遗传算法求解月球捕获制动和远程交会在月球惯性系下的轨道转移图. 图5 混合遗传算法最优解关于迭代次数的曲线Fig.5 The curve of optimal solution with iterations of hybrid genetic algorithm 从表1的数据可以看出,单纯形算法求解的速度增量的均方差为546.50 m/s,最大速度增量为2 581.0 m/s,而遗传算法求解的速度增量的均方差为3.38 m/s,最大速度增量为680.2 m/s,解的质量得到明显的改善,也说明了单纯形算法对初始点敏感,导致解的稳定性差.利用混合遗传算法求解的速度增量的均方差仅为0.14 m/s,最大速度增量也降低到666.6 m/s,相比于遗传算法的求解结果,解的质量进一步提高,这表明混合遗传算法对一体化制导问题能进行很好地求解. 图5和图6是为了验证本文混合遗传算法和规划模型的有效性.从图5中可以看出,总的速度增量在迭代160次之后又进一步降低,表明遗传算法搜索到的初始解,经过单纯形算法进一步优化,解的最优性进一步提高.图6中,登月舱所在的轨道周期为2.1 h,1~4表示飞船在进行机动时登月舱所在的位置,经过计算,飞船在5 h内经过4次脉冲的制导,到达指定的终点位置,表明本文一体化制导规划模型的有效性. 图6 飞船月球捕获制动和远程交会轨道转移图Fig.6Trajectory transfer diagram of lunar capture braking and far-range rendezvous of spacecraft 3) 不同时间下一体化制导仿真结果 图7 不同制导时间对结果的影响图Fig.7Influence diagram of different guidance time on results 为了研究在固定相位角差下,飞船通过4次脉冲实现月球捕获制动和远程交会一体化制导总的最优速度增量随着时间的变化.通过改变时间,获得飞船一体化制导总的最优速度增量、捕获制动时的速度增量和远程交会时的速度增量随着时间的变化曲线如图7所示.从图7可以看出,一体化制导的时间在1~3 h之间,最优总的速度增量随着制导时间增加而迅速降低,一体化制导的时间大于3 h时,最优总的速度增量变化较小,在666.3~666.6 m/s之间.捕获制动速度增量在前2 h内非常大,接近900 m/s;在2.5 h 时,速度增量最小,为300 m/s左右;3 h后速度增量增长幅度较小.远程交会的速度增量随着时间的增加而逐渐降低,3 h后减少的幅度较小.综合考虑任务周期和燃料消耗,在当前的相位角差下,一体化制导的时间选在大于3 h较为合理. 为了验证本文规划算法对全相位的强适应性,设置一体化制导时间为5 h,利用3.1中的初始仿真参数,初始时刻登月舱领先飞船不同的相位角差下,飞船通过4次脉冲实现月球捕获制动和远程交会一体化制导在登月舱的轨道平面内的相对运动轨迹图如图8所示. 图8 不同初始相位下的运动轨迹图Fig.8Trajectory diagram under different initial phases 从图8可以看出,飞船在全相位下都能到达指定的远程导引终点位置,表明本文的规划模型可以实现飞船在任意初始相位下的多脉冲一体化制导. 由3.1节可知,一体化制导最优总的速度增量与制导时间有关,图9是在登月舱领先飞船不同初始相位角差下,飞船经过四脉冲一体化制导最优总的速度增量和所需时间随着初始相位的变化图.可以看出,任意初始相位角差下,一体化制导最优总的速度增量均为666 m/s左右,但是所需要的一体化制导时间不完全相同.在不同的初始相位角下,可以根据本文的制导算法,选择合适的一体化制导时间,实现最小速度增量的轨道转移. 图9 不同初始相位下对结果的影响图Fig.9Influence diagram of different initial on results 使用装有Intel(R)Core(TM)i7-8750H 6核2.2 GHz CPU的计算机,运行MATLAB 2016a软件对四脉冲一体化制导的最优解进行求解,大约需要消耗4 min 的时间,时间消耗主要是动力学方程的积分运算.在地面任务设计中,混合遗传算法的时间成本是可以接受的. 本文以载人登月前载人飞船通过环月降轨与登月舱实现交会对接为背景,解决了月球捕获制动和远程交会一体化制导问题.本文基于Lambert变轨的方法,综合考虑时间约束、速度增量约束以及终端条件约束,设计了多脉冲捕获制动和远程交会一体化制导的规划模型,并且利用求解质量较高的混合遗传算法对规划模型进行求解.仿真结果表明,混合遗传算法可以有效提高求解质量,本文的规划模型正确有效,并且适用于任意初始相位差和不同时间内的多脉冲一体化制导,研究的结果对工程实践具有参考意义.2 基于串行混合遗传算法的一体化制导律的优化设计
2.1 一体化制导律的全局优化
2.2 一体化制导律的局部优化


2.3 一体化制导律的整体优化设计

3 仿真计算与结果分析
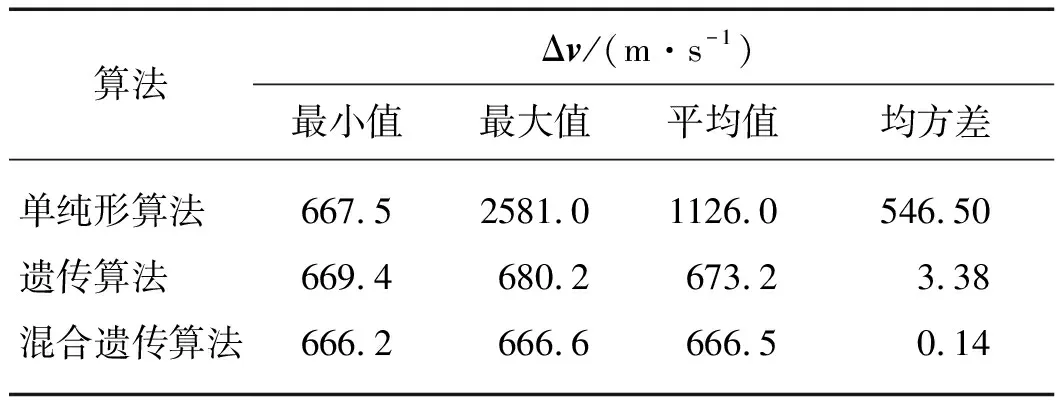
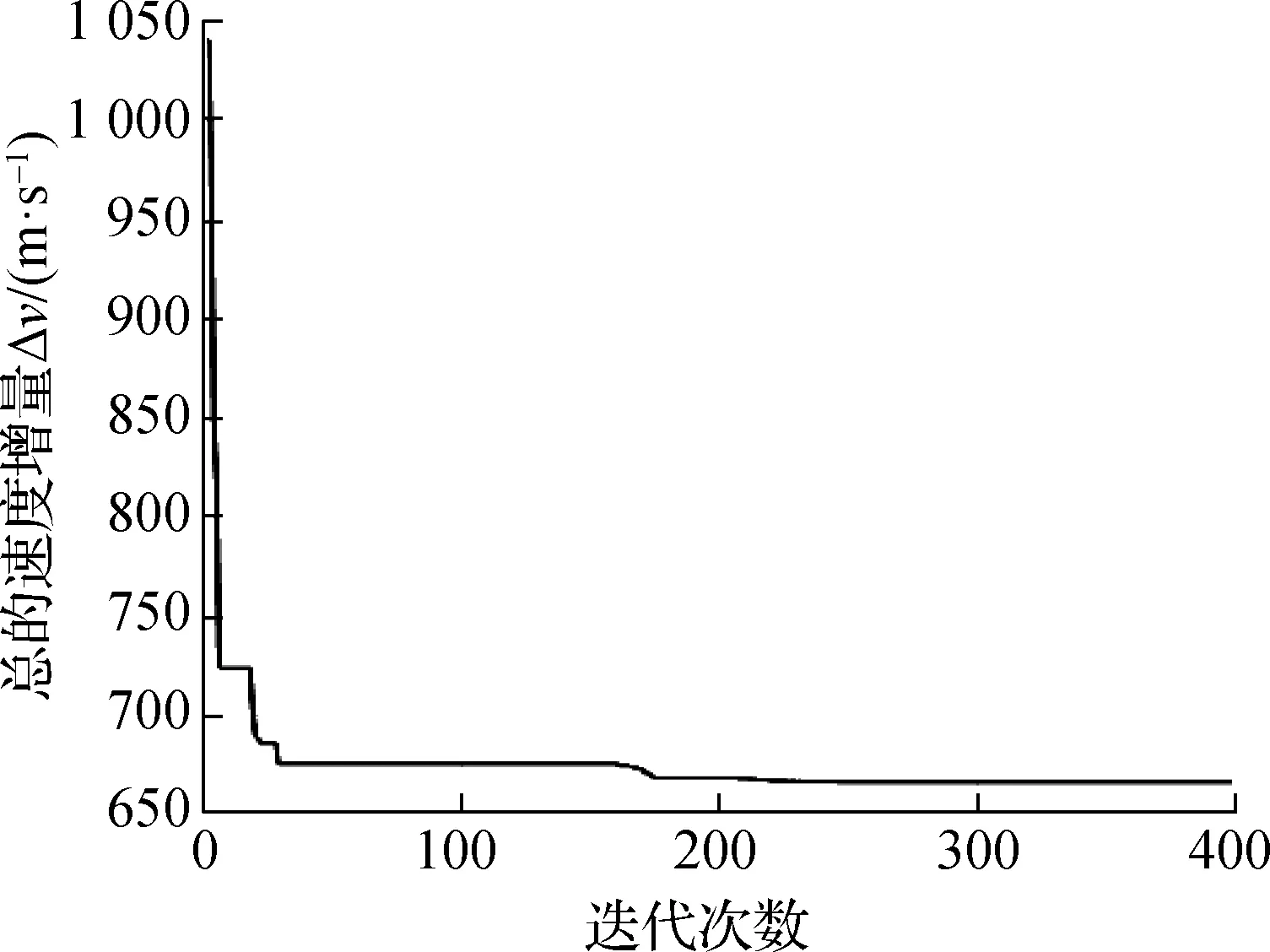
3.1 固定相位差下捕获制动和远程交会一体化制导仿真分析

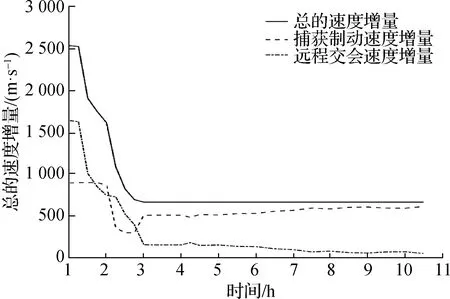
3.2 全相位捕获制动和远程交会一体化制导仿真分析


4 结 论

