基于混合自适应变异鸽群优化的飞机等效系统拟配

张兆宇,段海滨,2*，罗德林

(1.北京航空航天大学自动化科学与电气工程学院，北京100083；2.鹏城实验室，广东深圳518000;3.厦门大学航空航天学院，福建厦门361102)

电传操纵系统(fly-by-wire system，FBWS)的广泛应用极大地提高了飞机的飞行稳定性，使得现代飞机的模型阶次高达数十阶[1].通常现代战斗机的控制系统配备有多种补偿器、滤波器和传感器，纵向侧向运动耦合剧烈，长短周期模态之间以及横航向滚转螺旋等模态之间不易区分，且横向通道内容易发生耦合[1].美国有人给出驾驶飞机飞行品质规范MIL-F-8785C，提出一系列基于LOES(low-order equivalent system，LOES)开展评估的飞行品质标准.应用这些标准可以避免因模态耦合而剧增的计算复杂程度，为高阶增稳飞机控制回路设计提供工程意义上的参考.美军标在频率域上对等效拟配精度提出了失配度和失配包络线的要求[2].前者用一个与频响函数有关的代价函数在拟配频段内选取典型频率点计算拟配精度，而后者以包络线的形式在所选频段给出了整体的频响偏差要求.由此看来，研究复杂系统模型的低阶等效拟配方法，是完善高阶增稳飞机的飞行品质、评估体系和推动飞行控制系统发展的关键.

自等效系统的概念提出以来，最小二乘法(least square,LS)、极大似然法和模式搜索法等传统的寻优算法被用在等效系统的辨识中[3].由于流程简单、迁移便捷，LS在工程中应用十分广泛，但同时存在算法对初值设定依赖度高、不易收敛的缺陷[3].Kamali等[4]开发了非线性LS，用在飞行仿真器中辨识飞行品质参数.Shafer[5]使用极大似然法估计F-8C高增稳飞机的低阶等效系统.周堃等[6]使用LS工具箱对某型运输机的纵向通道进行拟配，并利用带宽准则、C*准则等典型飞行品质标准进行评价.王水英等[7]就拟合过程的初值选择、频率响应计算方式以及时延环节的线性近似等阐述LS求解等效系统的若干技巧.

由于缺乏LOES的参数先验知识，传统优化方法不易收敛的局限性造成算法初值选取的工作量繁重.故基于智能优化算法的若干等效拟配技术相继被提出，用于频域拟配，可避免其结果陷入局部最优.章萌等[8]将Tent混沌映射机制引入差分进化算法，对高阶飞机俯仰和过载通道实现频域双拟配.田宏峰等[9]设计了一种具有抗干扰能力的平均差分进化算法，在时域拟配俯仰通道和在含有不同程度的噪声输入下系统响应更佳.段效聪等[10]针对人机闭环系统模型，从克隆、变异、选择等自适应操作对克隆选择算法进行改进，以常规布局飞机为算例，完成巡航点的长短周期特性的等效系统拟配.

鸽群优化(pigeon-inspired optimization，PIO)算法是一种模拟鸽群借助太阳、地磁场和地标等导航工具归巢过程的仿生智能优化方法，通过两个不同阶段的导航机制，增强全局寻优能力和局部勘探能力[11].因其优秀的搜索性能和收敛能力，近年来在控制系统设计[12]、目标搜索[13]及参数辨识[14]等研究领域有广泛的应用.Deng等[12]利用改进的PIO求解频域等效系统参数，分析着舰控制系统的操纵性能；唐悦等[15]提出一种空天飞行器等效拟配方案，先使用LS的拟配结果作为优化初值，进而使用PIO辨识等效系统参数，提高了单独使用LS的拟配精度.由于美军标中对等效系统的计算有明确要求，纵向上要同时对俯仰和过载采取双拟配，横航向同时对滚转和侧滑双拟配[15].前文综述的工作有些仅针对纵向俯仰通道展开研究，另一些研究的飞机构型特殊且飞行状态考虑单一，或仅仅在结果中呈现了某一增稳通道的等效拟配结果.本文中将设计满足纵向与横航向双拟配的算法，并在本体模型和含增稳控制回路的闭环飞机模型上开展试验，避免上述各类局限性.

为了增强低阶等效系统的拟配精度，提高算法对不同高阶增稳模型的普适性，本文对基本PIO算法进行了改进，增加了鸽群内部在速度更新方面的随机交互学习，设计了一种地图与指南针算子的自适应调整策略，并受到差分进化算法启发，将衍生出的变异选择机制加入鸽子位置更新，提出混合自适应变异鸽群优化算法(mixed adaptive mutation pigeon-Inspired optimization，MAMPIO).本文以装有电传操纵系统的常规布局飞机为研究对象，对纵向通道的开环、闭环模型进行俯仰和过载双拟配仿真计算.为证明本文方法的有效性，将MAMPIO与经典PIO算法以及文献[8]中的混沌差分进化(chaotic differential evolution，CDE)算法进行试验对比，通过失配度大小和失配包络线量化分析其拟配效果.横航向通道低阶等效系统模型未知参数较多，使用MAMPIO进行拟配计算仍无法在试验频率段全部满足失配包络要求.故本文采用MAMPIO得到拟配结果后作为迭代初值，进一步采用LS搜索到失配度较低的低阶等效系统参数.在飞行包线内选取一些典型状态点进行等效拟配仿真.

1 问题描述与系统建模

本文中的评估对象包括飞机本体的纵航向模型、横航向模型，以及分别以俯仰角速率和滚转-航向速率为指令信号的增稳控制系统(control augmentation system,CAS).本文选取F-16“战隼”战斗机低保真度模型作为飞机算例，即在仿真分析时忽略前缘襟翼的舵回路效应.依据气动数据库的插值有效范围确定飞行包线，给出速度和高度约束.高度范围满足：1 524 m≤12 192 m，速度范围满足:91.44 m/s≤V≤274.32 m/s[16].

飞机的纵向和横航向的运动模态分离可利用小扰动理论实现，用状态空间表达为：

(1)

其中，各向量定义为:

(2)

其中：纵向的状态输出量中，俯仰角θ，空速Vt，迎角α，俯仰角速率q,法向过载nz;横航向状态输出量中，滚转角φ，侧滑角β，滚转角速率p，偏航角速率r；纵向输入中，δT为油门量，δe为升降舵量；横航向输入中，δa为副翼舵量，δr式为方向舵量.

考虑飞机本体小扰动模型，高阶系统的传递函数可以直接由式(1)所示的纵向或横航向状态方程计算得到.另外值得一提的是，本文还以带增稳控制回路的飞机高阶闭环系统作为等效拟配计算对象.将舵机动力学的非线性模型、相位滤波器和用以补偿调整稳定性的比例积分控制器、传感器等部分线性化处理，以获得能够作为拟配过程参考的高阶模型.

另外，研究纵向通道时，升降舵作动器的动力学特性可简化视为一个含系统时滞的一阶惯性环节.此外，舵回路的控制面铰链处通常存在有间隙非线性环节，且由于传感器与增稳控制回路中数字滤波器的存在会产生时滞特性[17].同理，对横航向通道中的副翼和方向舵可建立类似的非线性模型．

图2 飞机增稳控制系统模型结构Fig.2Control augmentation system structure for aircraft

作动器环节建模如图1所示，控制器输出的舵面指令信号分别经过一阶惯性动态环节以及包括间隙、时滞、饱和限幅等多个非线性环节后，输入状态空间模型.

图1 作动器非线性模型Fig.1Nonlinear model of actuator

为研究拟配算法在高阶增稳飞机模型的表现，本文以飞机算例开环本体模型为基础，分别为纵向和横航向通道设计了含有前馈控制器、阻尼器、传感器及滤波环节的增稳控制闭环模型，如图2(a)所示.由于评价纵向飞行品质大多是针对短周期运动进行双拟配，故图2(a)中考虑飞机短周期运动作为状态方程的闭环控制模型，其输入为俯仰杆力.与纵向增稳模型不同的是，评价横航向飞行品质需要对副翼到滚转角以及方向舵到侧滑角两通道的传递函数特性展开双拟配，模型输入包括侧向杆力与脚蹬量，故本文设计的横航向增稳控制闭环结构如图2(b)所示.图2(a)中，Flon、Flat、Fped分别表示俯仰、横向、脚蹬通道的杆力输入，δec代表升降舱指令偏度，ua和ur分别代表滚转和偏航通道输出的控制量.图1所示的作动器模型描述了图2(a)的升降舵回路和图2(b)的副翼与方向舵回路中的详细结构组成.

2 MAMPIO

经典PIO算法将鸽群的归巢路径搜索行为模拟为两个群体智能行为阶段，将待优化的参数向量视为鸽子在地图中的位置坐标.第一阶段模拟太阳与地磁场导航，完成基于指南针算子和全局最优信息的位置更新；待接近鸽群目标位置后，第二阶段则根据鸽群的健康度计算鸽群中心并设为地标，迭代一轮淘汰半数掉队的鸽子，剩余具有位置优势的鸽子继续搜索目标[11].

2.1 传统PIO算法

1) 地图与指南针算子

(3)

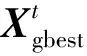
2) 地标算子

在第二阶段鸽群按照由群体健康度在每轮迭代计算群体的中心位置作为地标算子，鸽群中距离目标位置较近(即适应度较高)的子群会被保留，参考地标向目标位置飞行.第t轮迭代鸽群中第i只鸽子的健康度为：

(4)

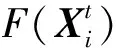
2.2 MAMPIO

以上两节中介绍了经典PIO算法在两个算子阶段作用下的迭代计算公式，该算法在处理高维度优化问题时，易陷入局部最优解.为改善局部勘探能力，本文介绍两种对经典PIO的改进策略，并将改进的MAMPIO算法用以解决高阶增稳系统的等效拟配问题.

1) 自适应权重调控算子

本节中提出两项作用于速度更新方程的自适应调控算子，随迭代动态调节搜索速度.

(5)

其次，将经典PIO中对局部最优解趋近项的随机权重更改为惯性自适应权重为：

(6)

(7)

其中:地图和指南针算子更换为自适应调控的Rt算子，r1和r2为两个在1和种群数量N间的随机整数，满足r1≠r2≠i.

2) 位置变异

在地图与指南针算子的每轮迭代中，在速度更新后加入对鸽群中每个个体的变异选择机制.由鸽子原位置叠加上差分位置变异项和平均速度变异项变异产生新个体，与原个体的适应度相比较选较优者，以增加搜索过程的多样性.

差分位置变异项计算了种群中随机个体同当前全局最优个体Gbestt间的距离，平均速度变异项基于当前鸽群速度平均值，采用柯西变异因子进行变异，对第i只鸽子变异得到的新个体位置可以表示为

(8)

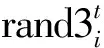
3 基于MAMPIO的等效拟配方法

本节中将介绍把以上的自适应调整机制和变异机制加入整个的MAMPIO算法流程，用来拟配低阶等效系统的完整方法.

飞机的低阶等效系统是指，在与高阶CAS受到同样的外界激励作用时，在飞行品质标准规定的时域或频域范围内，具有近似响应特性的可供等效分析的系统.由于高阶增稳飞机的各通道耦合严重，故很难根据传统的飞行品质评估方式通过区分不同运动模态来确定对应模态特性.军标中则推荐工程上通过频域辨识来确定低阶等效系统，并运用低阶系统的分析方法来评估飞机的品质.

由美军标MIL-STD-1797A可知，在频域上拟配低阶等效系统，主要思路为：设高阶系统在频率点ω处的幅值响应和相角分别为GHigh(iω)与ΦHigh(iω)，低阶等效系统的幅值和相角为GLow(iω)及ΦLow(iω).定义失配度M如下：

(9)

进行频域低阶等效拟配，要从0.1～10 rad/s按对数分段等间距取20个频率点，获得频率响应值，并按式(9)计算失配度，式中K值普遍取0.017 5.等效拟配的目标是尽可能减小失配度，使高低阶系统在频率域上具有较高的近似程度，目的是应用一些为等效系统设计的飞行品质标准，静态评估高阶CAS能否提升飞机在平飞、盘旋以及执行机动时的飞行品质.

本文对纵向高阶飞机增稳模型的俯仰和过载两通道采用双拟配，低阶系统模型为[2]:

(10)

使用PIO拟配时，可选择适应度函数如式(11)，为CAS模型在0.1～10 rad/s频率范围内按式(9)计算俯仰角速率通道与法向过载通道的失配度之和.对纵向高阶CAS模型双拟配所得参数向量包含两通道的7个特征参数[KθTθ2ζnspωnspτθKnτn]T，纵向总失配度的适应度函数可表示为：

(11)

对横航向的滚转和侧滑通道双拟配时，同样使用两通道的失配度之和构造适应度函数，军标中给出横航向的低阶系统模型可写为[2]:

(12)

横航向模型中期望拟配所得的参数向量为：

[TsTRζdωdKφζφωφτφKβTβ1

Tβ2Tβ3τβ]T.

在等效拟配中，将待拟配的参数向量映射为鸽子的位置信息，MAMPIO拟配步骤为：

Step 2:启动地图与指南针算子，根据式(5)、(6)计算自适应算子并更新指南针算子，根据式(7)更新鸽群速度，根据式(3)更新位置；

Step 5:启动地标算子，淘汰适应度较大的一半鸽子，更新鸽群位置，更新全局最优个体；

4 仿真试验与分析

本文在F-16算例的飞行包线内选取5组状态点，分别对纵向、横航向的本体模型、增稳控制闭环模型共4种模型进行等效拟配算法的对比仿真试验，以证明所提出算法的效果相较已有方法的优势.为了验证所提出的拟配算法具有全包线内普适且优异的性能，在以下状态点测试算法的拟配效果：①H=2 000 m,Ma=0.7;②H=6 000 m,Ma=0.8;③H=6 000 m,Ma=1.0;④H=8 000 m,Ma=1.2;⑤H=10 000 m,Ma=1.4.

在选取的5组典型状态点下分别以相同的初始参数进行仿真试验，得到纵向本体模型拟配结果和失配度值，如表1所示.由于篇幅有限，在图3(a)、(b)两图分别显示第①组和第④组状态飞机本体模型双拟配试验的失配度代价函数变化曲线，可据此直观了解各算法失配度变化过程，比较收敛和精度等算法性能.

表1 飞机纵向本体开环模型等效拟配结果Tab.1 Equivalent fitting result of longitudinal open-loop model

图3 纵向本体开环模型等效拟配适应度曲线Fig.3Equivalent fitting fitness curve of longitudinal open-loop model

表1中5组状态点的最佳拟配参数为最终达到最低失配度值的方法辨识得到的低阶等效系统参数，在此处均为MAMPIO方法的计算结果，且其失配度值远低于另两种方法.另由图3可见，CDE算法由于初始化存在Tent混沌映射， 会发生初始种群的改变而重新计算全局历代最优，映射效果不佳时会发生图中最优适应度在起初几次迭代升高的情况.PIO收敛速度尚可，但在各种测试条件下均更易陷入局部最优，造成最终失配度值偏高、精度偏低.而MAMPIO仅历约50次迭代可在引入变异因子的指南针算子作用下收敛到很低的失配度值，相较CDE和PIO，在收敛速度和变异寻优能力上具有显著的优势.

另外，考虑如图2(a)所示框架中含CAS的飞机纵向通道闭环模型作为研究算例，为CDE、PIO及MAMPIO 3种算法在5个状态组同上述开环模型仿真给定相同的初始参数，仿真对比飞机增稳闭环模型的双拟配结果.纵向增稳控制模型算例在5个仿真状态下的最佳拟配参数及失配度如表2所示.以第①组飞行状态的等效拟配结果为例，将高阶、低阶系统频率响应作为对比，以直观地展现3种拟配方法在整个拟配频段上的性能优劣，如图4所示.图4中(a)～(d)4张图分别展示了双拟配计算中俯仰、过载两通道的高低阶系统幅频、相频特性响应曲线，(e)和(f)两张图分别给出了两通道拟配频率段的各特征频率点的幅频失配度在失配包络线中的位置.图中蓝色实线以及浅红、浅蓝、浅黄虚线分别代表高阶系统频率响应以及CDE、PIO和本文提出的MAMPIO算法双拟配所得的低阶等效系统频率响应.

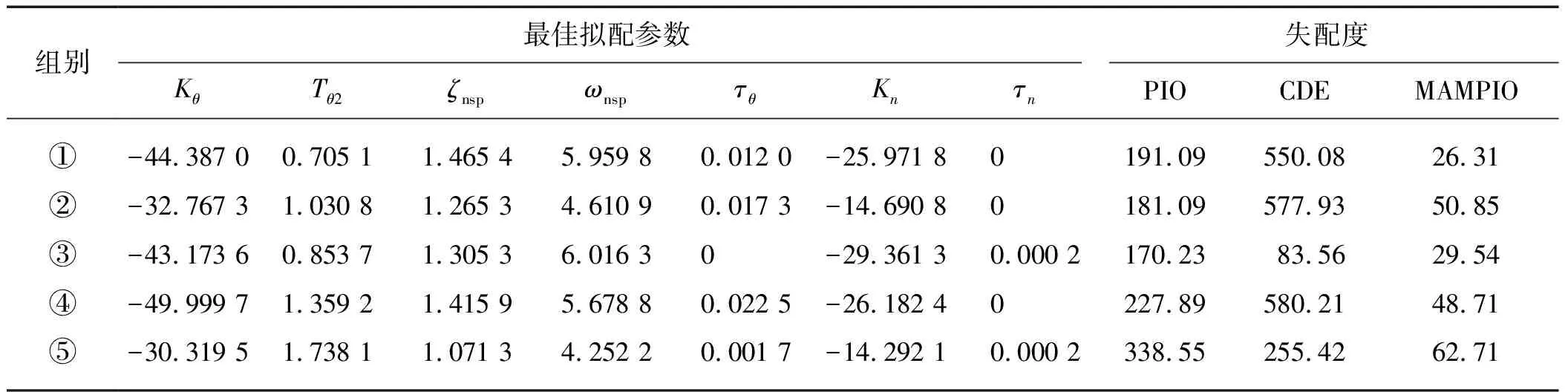
表2 飞机纵向闭环增稳系统等效拟配结果

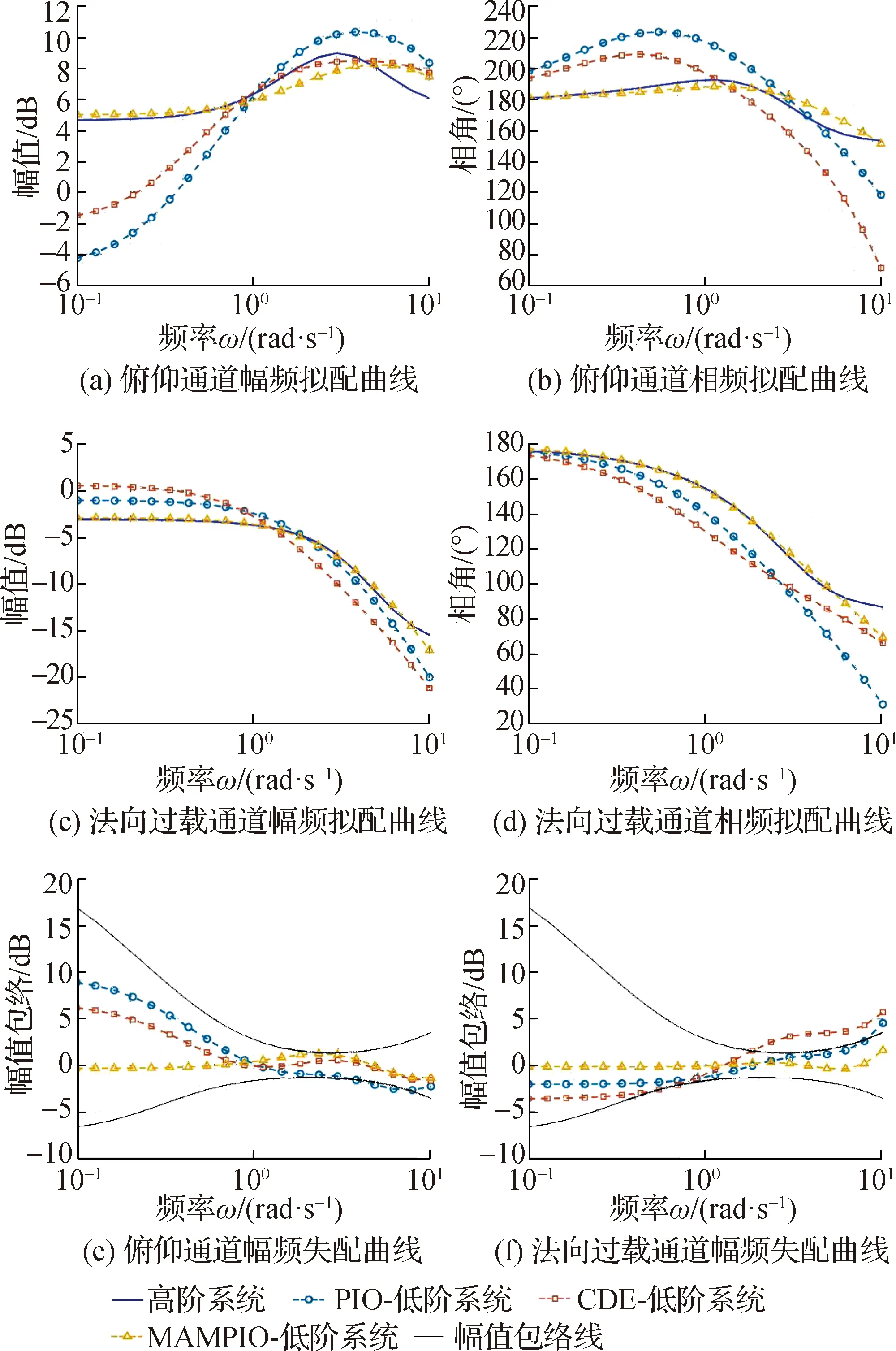
图4 第①组状态飞机纵向闭环增稳控制系统的拟配曲线Fig.4Fitting curve of longitudinal closed-loop CAS system for group ①

飞机的纵向增稳模型含控制系统以及作动器、传感器模型的非线性特性，由于该模型并不具有良好的小扰动特性，等效拟配相对困难.由图4结果可知，MAMPIO是3种算法中唯一能在等效拟配的全部频段均位于失配包络线以内的算法.由于计算失配度时对数等距取定频率点，在2～10 rad/s的中高频率段频率点间隔较宽，导致相邻频率点的频响特性变化相对更大.故由图4(e)和(f)可见，CDE和PIO在中高频率段超出失配包络线，而MAMPIO在变异因子作用下有效解决了该问题.综上，MAMPIO在纵向本体模型和高阶增稳模型的拟配中均达到较高的精度和收敛速度，且在飞行包线内选取的5个典型状态点的仿真结果均可以作为本文所提出方法在纵向通道可行性的有力佐证.

验证本文算法在横航向通道上的拟配效果，由于横航向低阶等效系统含有13个未知参数，且横航向的小扰动模型以及CAS相比纵向模型更复杂，计算难度高.本文算法在低频段具有良好的频率拟合特性，优于另两种算法；但因计算失配度函数的频率点以对数间距取定，在中高频段采样频率点数低于低频段，易出现失配度升高，故在多组状态点的仿真中采用文中的3种算法时侧滑通道的高频段拟配效果不佳.

为此，本文提出先使用MAMPIO初步辨识出一组低阶系统参数，再将参数向量作为初值，进而使用LS完成第二阶段的等效拟配.本文使用MATLAB官方给出的系统辨识工具箱中@lsqnonlin(fun，x0，lb，ub)求解代价函数为式(9)形式的非线性LS拟合问题，在函数形参中给定由横航向高阶、低阶系统模型计算的失配度函数、与MAMPIO相同的参数边界限幅以及由MAMPIO初步优化所得的参数初值，适合解决本文以LS形式为优化函数的横航向等效拟配问题[18].本节提出的先后分别使用MAMPIO和LS的组合拟配方法、MAMPIO-LS组合拟配方法和另3种纵向拟配中所对比算法在本文5组飞行状态仿真的失配度结果如表3左侧4列所示.由于篇幅原因，选取第③组状态，对比本节所提出MAMPIO-LS和CDE、PIO、MAMPIO 3种算法在对横航向飞机本体模型拟配效果曲线，如图5所示.图5(a)～(d)分别展示了在幅频和相频特性上滚转、侧滑两通道的LEOS与原高阶系统频率响应的对比曲线.仿真结果表明，单独使用MAMPIO的拟配效果优于CDE和PIO，但在侧滑通道高频段拟配效果很差，而本节提出的组合算法的失配度极低且在全部频段均位于失配包络线内.可见，此MAMPIO-LS的组合优化方法在横航向本体模型上拟配效果良好.

表3 飞机横航向模型等效拟配结果Tab.3 Equivalent fitting result of lateral directional model

再对横航向CAS高阶增稳模型进行双拟配计算.由于PIO和CDE在拟配横航向高阶增稳模型时失配度很高，且收敛速度极慢，则仅对比MAMPIO和MAMPIO-LS两种算法的拟配效果，在文中的5个状态点处计算收敛后的失配度结果如表3中右侧两列所示.仍以第③组状态为例，比较在滚转、侧滑通道上的频率特性如图6所示.由图6可见MAMPIO虽然在滚转通道上效果较好，但侧滑通道的中高频段拟配效果很差.这种现象仍是由于优化参数数量增加后，变异因子对各个参数的作用并不明显，导致无法收敛到最优值.而MAMPIO-LS算法仍旧在规定频段内均位于失配包络中，证明了该方法在横航向增稳系统上同样可靠.

图5 第③组状态飞机横航向本体开环模型拟配曲线Fig.5Fitting curve of lateral directional open-loop model for group 3

5 结 论

本文提出了一种基于混合自适应变异机制的PIO算法，分别用于纵向、横航向的飞机本体模型与增稳控制模型的等效拟配.将MAMPIO算法应用在飞机纵向本体模型和增稳控制模型的双拟配试验中，在本文所选的飞行包线内5个典型状态点处性能表现良好，拟配精度显著高于另两种对比的优化方法.在横航向通道的双拟配试验中单独应用MAMPIO在低频段拟配良好，高频段效果不佳；本文进而设计了 MAMPIO粗略搜索低阶系统参数，并作为LS初值继续迭代寻优的两阶段拟配方法，在横航向的高阶增稳模型双拟配试验中改善了侧滑通道高频段的拟配效果.

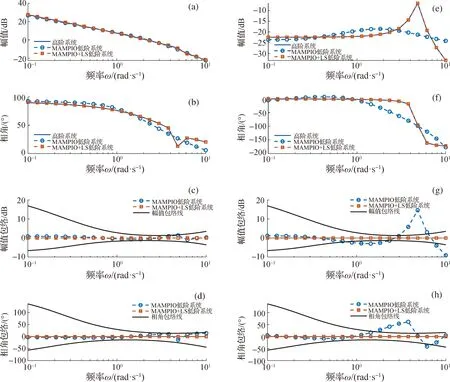
(a)～(d)为滚转通道频率特性失配曲线，(e)～(f)为侧滑通道频率特性失配曲线.图6 第③组状态飞机横航向闭环增稳控制系统拟配曲线Fig.6Fitting curve of lateral directional closed-loop CAS system for group ③