抗饱和控制系统研究综述

赖文馨，李元龙*，林宗利

(1.上海交通大学电子信息与电气工程学院，系统控制与信息处理教育部重点实验室，上海工业智能管控工程技术研究中心，上海200240；2.美国弗吉尼亚大学电机与计算机工程系，夏洛茨维尔22904-4743)

在实际工程系统中，由于物理结构的限制以及安全运行的要求，执行器驱动输出信号的幅值和变化速率都有界限，会引发执行器饱和现象.例如，无人机舵面的偏转角度和偏转速率是有限的，汽车舵机系统中舵机的转动功率及转动速度也存在限制等.当执行器发生饱和时，被控对象接收到的驱动信号偏离控制信号，导致闭环控制系统性能下降，在极端状况下甚至会导致系统不稳定，造成严重后果.典型案例有1989年瑞典JAS-39“鹰狮”战斗机坠毁，事故原因在于执行器饱和引发的机体不稳定振荡[1].因此，自20世纪80年代开始，执行器饱和问题得到人们广泛关注，并逐渐成为控制系统中的一个热点研究问题.

一般来讲，处理执行器饱和的方法可分为直接法和间接法.直接法的思路是，在控制器设计时考虑执行器饱和，直接将饱和非线性的处理融入控制器设计中[2-12].间接法又可称为抗饱和控制方法，其基本思想在于分离控制器设计和饱和处理过程，即先在不考虑执行器饱和的情况下设计满足性能要求的控制器，再设计补偿器来尽可能消除执行器饱和带来的负面影响.这种阶段式的设计方法思路清晰.抗饱和补偿器一般在执行器发生饱和时被激发，以此来减弱执行器饱和导致的系统性能下降，并促使执行器退饱和；在不发生饱和时闭环系统将保持线性特性，从而达到确保抗饱和控制系统性能要求的目的.

抗饱和控制起源于工程实践，相关研究可追溯至20世纪30年代[13].早期研究发现，控制器含有的积分项不断积累期望信号与输出信号的偏差，导致控制信号超出执行器的物理上限，从而引发积分器溢满(integrator windup)现象[14].当初解决这一问题的方法是构造补偿器，使其信号馈入到控制器中以达到退饱和的目的，即前文介绍的间接法，也被称为抗积分器溢满(anti-windup)控制方法，可简称为抗饱和控制.在抗饱和控制发展的初始阶段，人们做出了许多尝试，采用了诸如描述函数法[14]、回馈计算(back-calculation)[15]、条件技术(conditioning technique)[16-18]等方法对饱和约束系统进行研究，提出了基于观测器[19]、智能积分[20]、高增益反馈[21]等多种补偿器设计方法.20世纪80—90年代，抗饱和控制的统一框架得到进一步确定和发展[22-27]，同时结合输入受限控制[2,6-9,28]、H∞控制[29-31]等方法和技术，逐步形成较完整的抗饱和控制研究体系，为稳定性及性能等问题的研究提供严谨的理论保障.该阶段的抗饱和控制不仅在理论层面上涌现出了相当可观的研究成果[32-40]，同时也在诸如飞行器[41-43]、电机[44-45]、机器人[46-48]等工业领域上展现出了强大的应用潜力.

1 抗饱和控制一般框架

考虑具有执行器饱和的线性系统如下：

(1)

其中，xp∈Rnp是被控对象的状态，u∈Rnu是执行器输入信号，ω∈Rnω是外部输入信号，y∈Rny是系统输出信号，z∈Rnz是性能输出信号，Ap、Bpu、Bpω为适维常数矩阵，饱和函数sat(·):Rnu→Rnu定义为

其中ulim代表饱和函数的饱和幅值.

针对被控对象(1)，设计线性控制器如下：

(2)

其中，xc∈Rnc是控制器的状态，u∈Rnu是控制器输出信号，同时也是执行器输入信号，Ac、Bcy、Bcw、Cc、Dcy、Dcω为适维常数矩阵.在无执行器饱和的情况下，被控对象(1)与控制器(2)构成的闭环系统渐近稳定且具有期望的闭环系统性能.

为了解决执行器饱和引发的系统性能下降问题，设计抗饱和补偿器如下：

(3)

其中：xaw∈Rnaw是抗饱和补偿器的状态,v1∈Rnc和v2∈Rnu是抗饱和补偿器的输出信号，依赖于信号u和y,且v1输入到控制器中，v2被直接馈入执行器输入信号中.在该抗饱和补偿器的作用下，控制器(2)可重新描述为

(4)

如图1所示，被控对象(1)，控制器(4)以及抗饱和补偿器(3)三者共同构成抗饱和控制系统的基本框架，其中抗饱和补偿器在执行器发生饱和时被激发.

一般来说，抗饱和补偿器的设计应达到以下控制目标：

1) 当未发生执行器饱和时，闭环系统处于未受限的线性状态，需要满足期望的性能要求；

2) 当发生执行器饱和时，闭环系统的响应要尽可能地接近未受限系统的响应.

抗饱和设计过程中，具体的问题需要考虑不同的优化目标.例如，吸引域大小是衡量闭环系统稳定性能的一个基本指标，而抗饱和补偿器的引入需实现闭环系统吸引域的最大化；又如，在存在外部输入的情况下，通过设计抗饱和补偿器，使闭环系统满足一定的L2增益[32]性能指标.

2 抗饱和控制研究现状

正如图1所示，抗饱和控制系统的核心在于引入合适的抗饱和补偿器，该过程包含两个重要方面，分别是抗饱和补偿器的结构设计及激发机制.围绕这两方面，目前已经涌现出了相当数量的研究成果.接下来，将分别从这两个方面对已有研究成果进行梳理与总结.

2.1 抗饱和补偿器结构设计

现有抗饱和补偿器有两类，一类是直接型结构，另一类是基于模型恢复，其中后者须包含被控对象的结构信息.

1) 直接型抗饱和补偿器

直接型抗饱和补偿器不显含被控对象的模型结构和参数，在设计上具有较高的自由度.近几十年来，已经涌现了丰富的线性及非线性的补偿器结构设计成果.得益于成熟的线性系统理论体系，线性结构的抗饱和补偿器设计得到了充分的发展.Grimm等[33]分别提出了静态以及动态抗饱和补偿器的综合方法，并给出了一个有趣的结论，即对于开环稳定的系统，必然存在一个与被控对象阶数相同的动态抗饱和补偿器，其L2增益为开环系统L2增益与线性闭环系统L2增益中的较大值.随后，Hu等[49]在上述工作的基础上，针对开环不稳定的系统，给出了能确保局部L2增益性能的抗饱和补偿器的存在条件和构造方式.Cao等[34]和Gomas等[50]为了实现闭环系统吸引域的最大化，分别基于凸包表示法和局部扇区条件给出了静态抗饱和补偿器的设计方法.Wu等[51]分别针对幅值和速率同时饱和的线性系统以及仅幅值受限的线性分式变换(linear fractional transformation)系统，确立了抗饱和补偿器存在的线性矩阵不等式条件，并给出了详细的补偿器构造步骤，改善了闭环系统的性能.刘晨等[52]考虑具有外部扰动输入的不确定系统，以扩大其收敛域为目标，构建了以不确定项和扰动输入为增广状态的增广系统，给出了基于扩张状态观测器的动态抗饱和补偿器设计方法.除此之外，与抗饱和控制的阶段式设计方法不同，Mulder等[53]保留了抗饱和控制的基本框架，提出线性控制器与抗饱和补偿器同时设计的方案，在一定程度上融合了直接法和间接法的优势.Cao等[54]则采用含有抗饱和补偿器结构的智能积分控制器，提出一种基于线性矩阵不等式的求解算法，以确定控制器的反馈增益和抗饱和补偿器增益，扩大了闭环系统吸引域.

与线性结构的抗饱和补偿器不同，非线性抗饱和补偿器的结构复杂，设计上更具难度.但通常来说，非线性抗饱和补偿器能够提供更好的控制性能，尤其当线性补偿器不足以应对执行器饱和造成的稳定性及性能问题时，非线性抗饱和补偿器将是一个选择.对于直接型抗饱和控制而言，较为普遍的是采用非线性策略来调度一组线性抗饱和补偿器.例如，Lu等[55]利用复合二次型Lyapunov函数，给出了一组静态补偿器增益的求解算法，并通过复合Lyapunov函数中的复合函数融合这些静态补偿器，构建了非线性抗饱和补偿器.除此之外，切换策略也在非线性补偿器设计中得到应用.比如，针对扩大吸引域问题，Lu等[56]基于最小二次Lyapunov函数蕴含的最小值函数，设计了一组线性抗饱和补偿器增益进行切换控制；Li等[57]对表示饱和函数的凸包进行分区，并为每个凸包分区分配相应的静态补偿器，再根据饱和信号所处的凸包分区来激发对应的补偿器，形成了切换抗饱和补偿器，从而实现了闭环系统吸引域的扩大.

2) 基于模型恢复的抗饱和控制

与直接型抗饱和补偿器灵活的设计方式不同，基于模型恢复的抗饱和控制必须根据被控对象的模型信息G(s)来构建补偿器(补偿器由M(s)-I和G(s)M(s)构成)，其核心在于从含有执行器饱和的闭环系统中析出未受限的线性系统，并最小化剩余部分的系统增益，达到使闭环系统动态性能尽可能地逼近未受限系统的目的，其控制框图如图2所示.

图2 基于模型恢复的抗饱和控制的基本控制框图Fig.2The basic control framework of the model recovery anti-windup control

为了更好地解释基于模型恢复的抗饱和控制的基本原理，可将图2所示的基本框图等价转化为图3中的控制框图[36].

图3 基于模型恢复的抗饱和控制的等效表达Fig.3An equivalent representation of the model recovery anti-windup control

图3中的等效表达解除了系统线性部分与非线性部分的耦合，清晰地划分出基于模型恢复的抗饱和控制的3个重要构成部分，分别是提前设计的具有期望性能的未受限系统、包含死区函数的非线性环及含有被控对象模型信息的扰动滤波器.其中，扰动滤波器产生的信号yd表达了实际饱和约束控制系统与理想未受限系统之间的差异.在该控制框架下，系统的响应行为分为3个阶段[36].第一阶段，执行器未发生饱和，系统处于线性工作状态；第二阶段，控制输出ulin超出了饱和限制，执行器发生饱和，扰动滤波器产生信号yd,影响未受限系统的输出ylin；第三阶段，执行器退出饱和状态，但由于扰动滤波器的动态结构，信号yd依旧存在，持续影响信号ylin.作为唯一的可设计参数，传递函数M(s)的恰当选择可使系统处于第二阶段和第三阶段的总时长最短，从而使实际饱和约束控制系统的响应尽可能恢复至未受限时的状态.基于模型恢复的抗饱和控制具有清晰直观的物理含义，其补偿器的构造仅需考虑对系统非线性部分的分析.然而，正如图3所示，基于模型恢复的抗饱和控制必须根据被控对象的动态机理构建抗饱和补偿器，导致该类抗饱和补偿器的基本结构固定，缺乏灵活设计的自由度.

根据基于模型恢复抗饱和控制的思想，Galeani等[58]针对开环稳定的系统，设计了一种非线性调度技术来实现一组线性抗饱和补偿器的切换.Zaccarian等[59]则考虑指数不稳定的被控对象，提出了一种构造性的非线性抗饱和补偿器设计，获得了预期的跟踪性能.Grimm等[60]将预测控制与基于模型恢复的抗饱和相结合，把抗饱和设计问题转化成了具有约束限制的滚动时域优化问题.Turner等[37]和Li等[61]则致力于将鲁棒性指标融入到基于模型恢复的抗饱和补偿器设计中，有效地改善了系统性能.Turner等[38]则在直接型抗饱和控制框架下，提出了基于模型恢复的静态及低阶抗饱和补偿器构造方案.此外，针对特定结构系统的抗饱和控制研究也不少.比如，Ofodile等[62]提供了针对输入耦合双积分系统的抗饱和补偿器构造方式，并基于无人机实验平台验证了该补偿器在改善闭环系统跟踪性能方面的有效性；Lv等[63]针对具有输入饱和的线性多智能体系统，设计了基于模型恢复的分布式抗饱和补偿器，解决了其一致性问题.

2.2 抗饱和补偿器激发机制设计

抗饱和控制的基本思想是设计并激发补偿器，将其信号馈入到控制器中，从而抑制执行器饱和带来的系统性能下降.激发机制的设计，也就是何时启动抗饱和补偿器，是影响闭环系统性能的重要因素.因此围绕如何设计补偿器的激发机制问题，学者们给出了一系列研究成果.

传统抗饱和补偿器激发机制可称为立即激发，即在执行器发生饱和时立即启动抗饱和补偿器，这种依赖于执行器饱和状况的设计是自然而然的，也是研究和应用最多的一种激发机制.立即激发机制一般拥有两种表现形式.第一种见于直接型抗饱和控制，可参见文献[49-53]，这种驱动形式利用执行器输入与输出的信号差值启动抗饱和补偿器，其结构形式简单直观，如图 4(a)所示.而另一种驱动形式用于基于模型恢复的抗饱和控制，如文献[58-65]所述，其具体结构请见图4(b).尽管这一结构会产生代数环，使得抗饱和系统更复杂、补偿器设计更具难度，但文献[27,65]表明，该代数环能够有效改善闭环系统的暂态性能.此外，针对特殊的饱和约束控制系统，立即激发机制可根据系统的结构特点进行相应的调整.例如，在线性反馈嵌套饱和系统中，嵌套饱和结构不可拆解，是一个整体非线性环节[66].对此，抗饱和补偿器不再由单一的饱和非线性驱动，而是由控制器输出和被控对象输入之间的差信号驱动，包含着多重嵌套饱和信息.

图4 立即激发机制的基本结构Fig.4The basic structures of the immediate activation mechanism

值得注意的是，尽管一般而言，饱和的存在会对系统性能产生负面影响，但若执行器过早地退饱和，被控对象的驱动信号随之减弱，会造成闭环系统暂态性能的降低；因此适当地维持执行器饱和，在合适的时间段内提供较大的驱动信号，有助于改善系统暂态性能.考虑到这一点，Sajjadi-Kia等[67]提出了一种延迟激发机制，即在控制信号幅值超过执行器饱和值一定程度后才启动抗饱和补偿器.该激发机制需要引入一个虚拟饱和环节，其饱和值略高于实际执行器的饱和值.如图5所示，延迟激发的抗饱和补偿器由该虚拟饱和环节输入输出的差信号驱动.

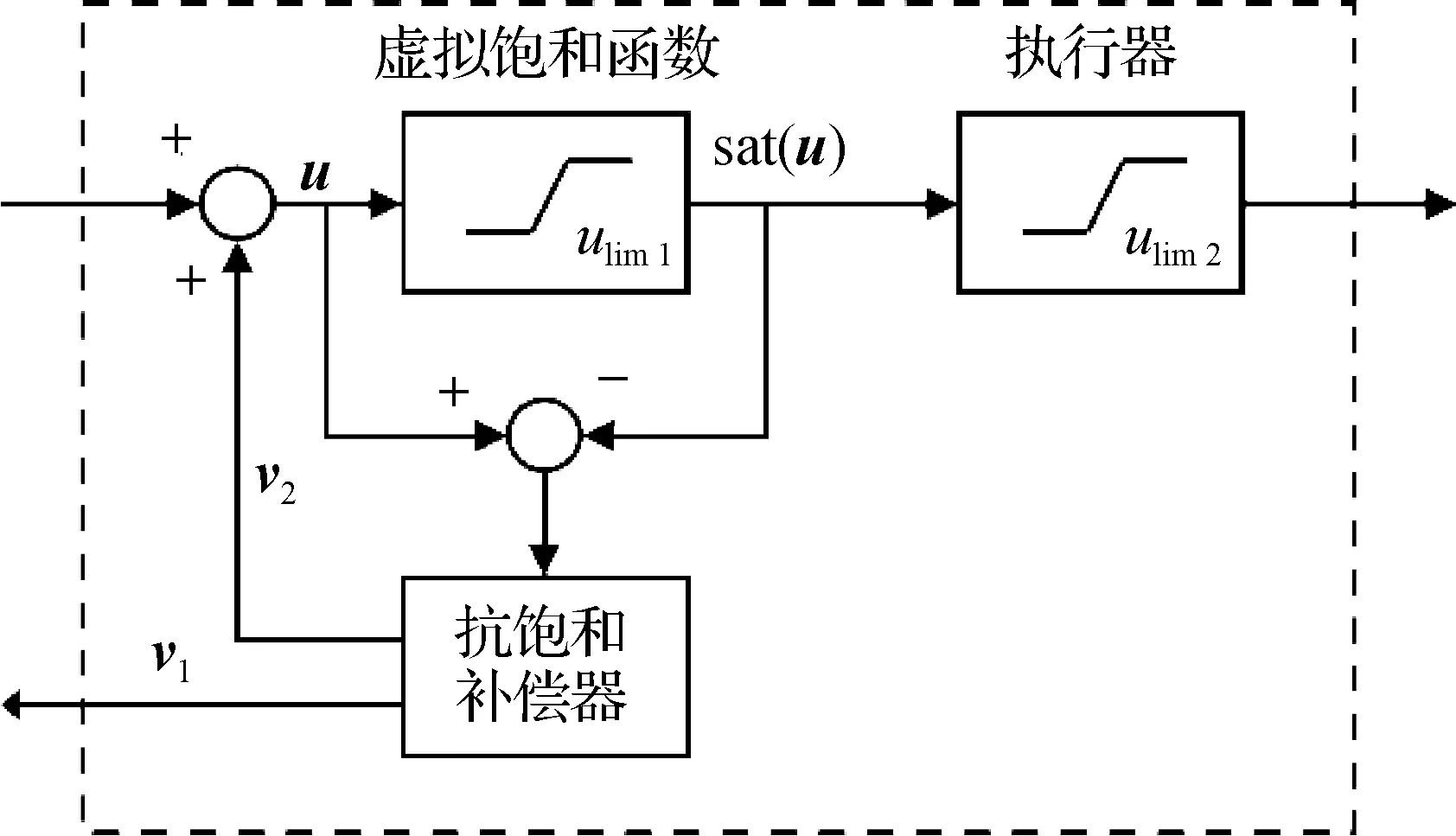
图5 延迟激发机制的基本结构Fig.5The basic structure of the delayed activation mechanism

延迟激发机制在一定程度上改善了闭环系统的暂态性能，并在幅值与速率同时饱和的系统中得到了扩展应用[68].与延迟激发机制不同，Wu等[69]提出了提前激发策略，即在控制信号幅值尚未达到执行器饱和值时，提前启动抗饱和补偿器，可以起到未雨绸缪的作用.与延迟激发相似，提前激发机制同样需要引入虚拟饱和环节，区别在于其饱和值需要略低于实际执行器的饱和值，以达到提前激发的目的，具体结构可见图6.相较于立即激发和延迟激发，提前激发不仅可以改善闭环系统的信号跟踪性能，还能有效扩大闭环系统的吸引域.随后，Turner等[70]给出一种包含两种死区非线性的类扇区条件，并为提前激发抗饱和补偿器提供了具有更优数值特性的构造方式.在文献[70]的基础上，Turner等[71]进一步完善了类扇区条件，提出一种两阶段并联型抗饱和控制框架，如图7所示，并指出现有的激发机制皆可解释为该控制框架下的特殊情况.

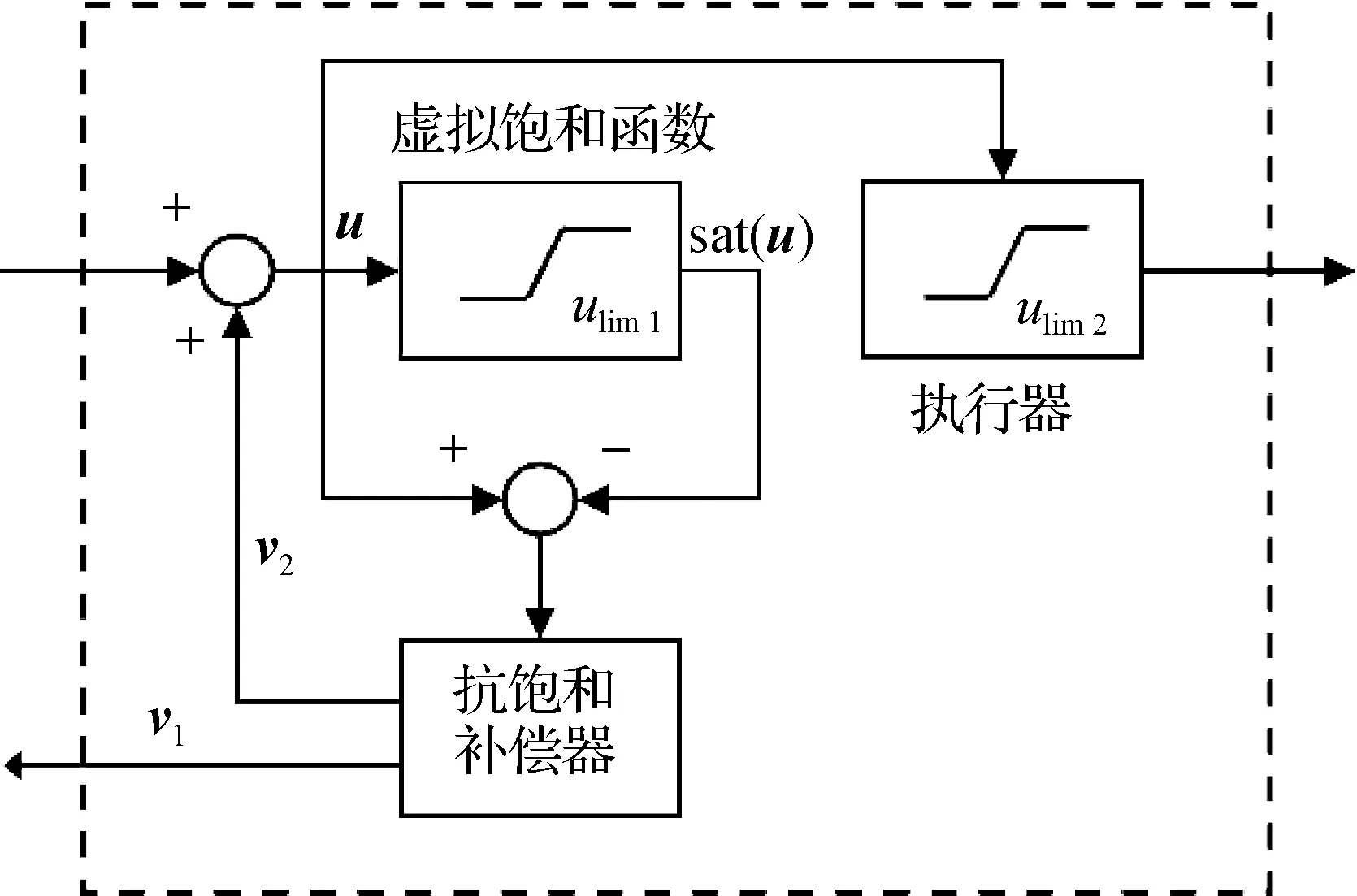
图6 提前激发机制的基本结构Fig.6The basic structure of the anticipatory activation mechanism

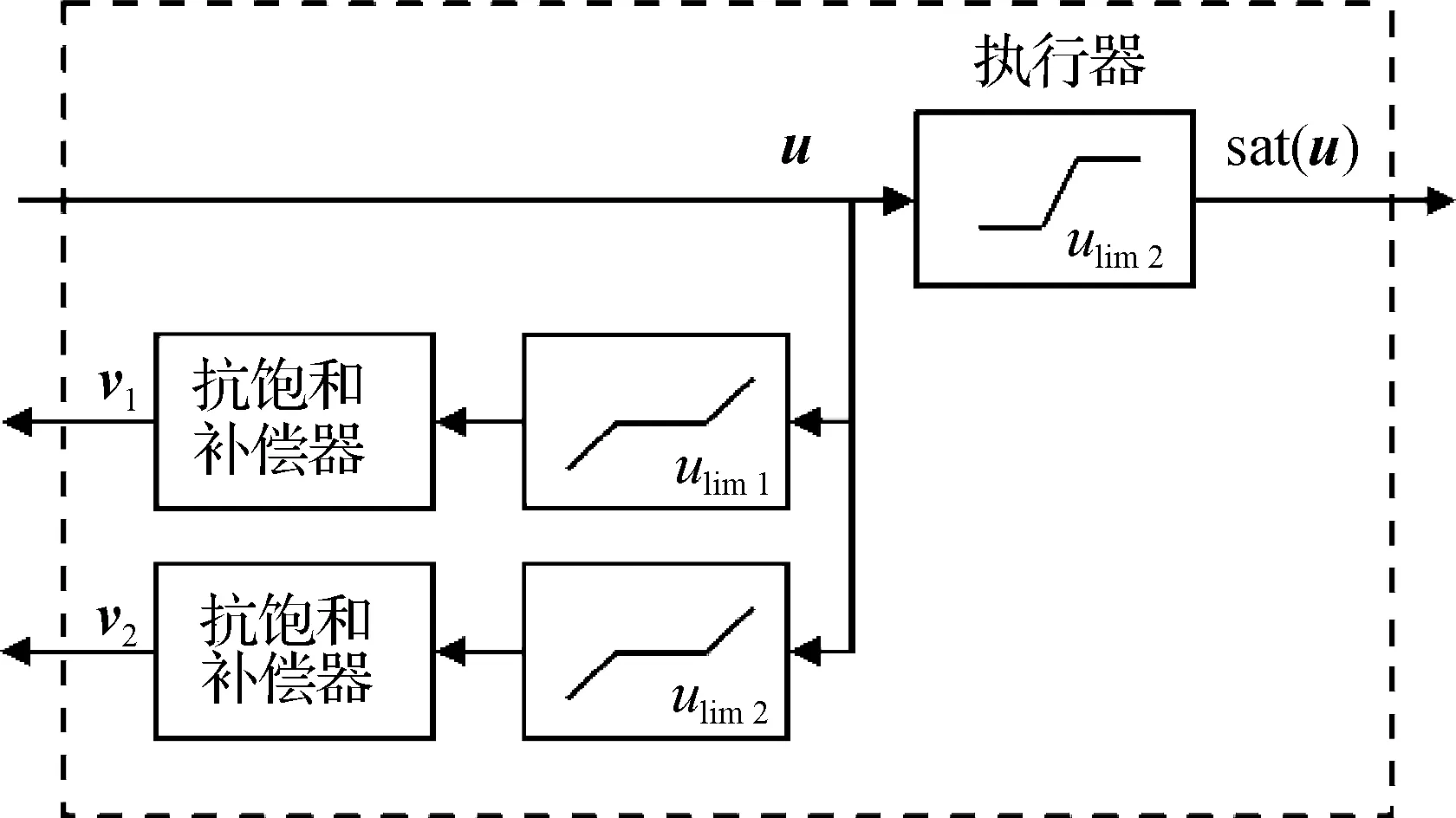
图7 两阶段抗饱和控制框架Fig.7The two-stage anti-windup control framework

事实上，单一激发机制的缺点较为明显，即对不同饱和程度的控制信号采取相同的激发策略，那么更优的做法应该是针对不同幅值的控制信号设置相应的激发机制.基于这种考虑，混合激发机制的方法应运而生.例如，Sajjadi-Kia等[72]针对开环稳定的系统设计了延迟激发和立即激发相结合的多阶段抗饱和控制框架，并分别给出了静态和动态抗饱和补偿器的设计方案，保证了闭环系统L2增益性能；彭秀艳等[73]采用了和文献[72]相同的混合激发机制，通过衡量饱和约束系统的控制器状态与未受限系统的控制器状态的差异来对抗饱和补偿器进行优化设计，当控制信号的饱和程度较高时，两种激发机制驱动的补偿器同时工作以改善闭环系统性能，当执行器处于微饱和状态时，单一补偿器启动，以降低闭环系统工作负担.Wu等[74]则通过融合立即激发、延迟激发以及提前激发的各自优势，提出了一种兼具3种激发机制的多环抗饱和控制框架，比起仅结合两种激发机制的方法，该方法更能提高闭环系统的跟踪性能.

3 拓展研究

实际控制系统中的执行器饱和大部分不是简单的对称饱和，会呈现出如嵌套饱和、非对称饱和等形态，另外系统输出端的传感器也会出现饱和现象，即输出饱和.针对不同形态的饱和非线性，其抗饱和补偿器的设计各有特色.由于实际的被控对象也多是非线性的，面向非线性控制系统的抗饱和设计得到了重视.目前，多智能体系统已成为控制领域的研究热点，其抗饱和控制的研究也得到了大量关注.

1) 嵌套饱和

嵌套饱和是一种更复杂的饱和约束，在实际控制系统中也较为常见.例如，幅值与速率同时饱和可建模为嵌套饱和[68].又如，执行器饱和与传感器饱和同时存在时可用嵌套饱和表征[75].在嵌套饱和系统的抗饱和控制问题上，相关研究工作已经开展.Wu等[51]针对幅值与速率嵌套饱和系统，提出基于扩展圆判据的抗饱和补偿器综合条件，并建立优化问题以设计补偿器，最后通过飞行控制仿真实验验证了补偿器的有效性.Galeani等[76]将嵌套饱和等价地表示为单层饱和，简化了嵌套饱和系统抗饱和补偿器的设计复杂度.Reineh等[77]采用文献[78]中提出的软件模拟法进行速率饱和建模，并将补偿器馈入控制器的部分补偿信号再馈入到执行器输入中，打破了传统设计中两个补偿信号互不干涉的设计模式，从而改善了闭环系统的暂态性能.Gomes等[79]则把基于单层饱和系统的线性控制器和抗饱和补偿器同时设计方法[53]，拓展到嵌套饱和系统中，扩大了闭环系统的吸引域.此外，Glovanini[80]融合了预测控制与抗饱和控制的思想，提出了基于滚动时域优化策略的抗饱和补偿器设计方案，并将其应用到幅值与速率嵌套饱和系统中.

2) 非对称饱和

在实际系统中饱和非线性有时以非对称的形式出现.饱和的非对称性为抗饱和设计带来了困难.目前对于非对称饱和的抗饱和研究不多，其研究依赖于非对称饱和函数的处理.处理非对称饱和的常见方法是将其转换为对称饱和，而后依此设计抗饱和补偿器.例如，Yuan等[81]将非对称饱和系统等价成切换系统，每个子系统含有不同饱和值的对称饱和函数，并分别针对每个子系统进行独立的补偿器设计，最终形成切换抗饱和补偿器；Li等[82]将非对称饱和函数分解为常数项和对称饱和函数，并将常数项视为已知幅值上限的扰动输入，从而将非对称饱和系统的抗饱和问题转化为具有扰动输入的对称饱和系统的抗饱和问题；Geng等[83]采用与文献[82]相同的非对称饱和处理方法，将析出的常数项和模型误差作为系统增广状态，提出一种基于扩张状态观测器的静态抗饱和补偿器设计方法，改善了非对称饱和系统的抗干扰能力和跟踪性能.

3) 输出饱和

由于物理结构的限制及外部环境的干扰，传感器也会发生饱和现象.当传感器饱和时，控制器被馈入不准确的测量信号，会导致闭环系统性能下降.与执行器饱和本质不同的是，传感器饱和与否是无法测量的，因此其抗饱和方法无法依赖传感器的饱和状况，需要设计辅助环节来估计传感器输出端是否发生了饱和，故加大了传感器饱和系统抗饱和设计的难度.Tarbouriech等[84]和Turner等[85]通过设计状态观测器及引入新的饱和环节来模拟传感器，将该虚拟传感器输入输出信号的差值用以驱动抗饱和补偿器，并给出了补偿器的存在条件和构造方式；但因其引入了非线性环节，导致闭环系统结构更加复杂，增加了分析系统稳定性和性能的难度.Turner等[86]将状态观测器输出与实际传感器输出的差值作为修正状态观测器的反馈信号，并利用其直接驱动补偿器，无需引入新的非线性环节，明显改善了闭环系统的信号跟踪能力.除此之外，Sofrony等[87]借鉴故障诊断所使用的基于互质分解法的残差生成技术[88]，利用该残差信号驱动抗饱和补偿器，从而将输出饱和系统的补偿器设计问题简化为求解合适的被控对象互质分解结果和其对应的Bezout补偿.Sassano等[89]则针对单输入单输出的离散输出饱和系统提出一种逻辑切换策略，以实现输出反馈信号在传感器输出和状态观测器输出之间的切换，并在此基础上设计了基于模型恢复的抗饱和补偿器，实现了有限时间内闭环系统响应恢复到未受限状态的目的.

4) 非线性被控对象

非线性被控对象的抗饱和控制基本上也采用了和线性被控对象相似的结构框架.例如，Herrmann等[90]针对含有非线性动态逆控制器的闭环系统，设计了一种通用的基于模型恢复的抗饱和补偿器结构框架.刘胜等[91]采用线性微分包含方法处理系统非线性项，利用一组线性模型的凸组合表达不确定非线性系统，基于此提出了一种静态抗饱和补偿器增益求解方法.此外，自适应控制以及神经网络也在非线性被控系统的抗饱和控制中得到应用.例如，Kahveci等[92]提出一种鲁棒自适应方法用以在线估计滑翔机系统的模型参数，根据所得参数，利用互质分解法在线优化并更新抗饱和补偿器增益，使滑翔机拥有良好的轨迹自主跟踪性能；Ji等[93]则针对固体氧化物燃料电池系统，采用神经网络方法对其动态机理进行建模，基于此求得被控对象输出到控制输入的Jacobian信息作为抗饱和补偿器增益，最终实现了维持合理的燃料使用率的目标.

5) 多智能体系统

输入饱和作为控制系统的一种常见约束，对多智能体系统的一致性问题及相关问题的研究增加了难度；抗饱和控制则为这些问题的解决提供了行之有效的方法.Lim等[94]为饱和异构多智能体系统引入静态抗饱和补偿器，促使饱和的参考信号回到线性工作区域，从而形成有界参考轨迹，并最终实现了状态的局部一致性.Li等[95]考虑饱和多智能体系统的领导-跟随状态一致性问题，为每个跟随者设计相应的静态抗饱和补偿器，确保了饱和情况下多智能体系统的稳定性与性能要求.Fu等[96]针对有向通信情况下的二阶多智能体系统，提出一种分布式抗饱和控制策略，该策略能够灵活适应不同局部性能的线性控制器，实现了对饱和非线性的有效处理以及保持全局状态一致性的目的.Lv等[63]与Richards等[97]提出基于模型恢复的动态抗饱和补偿器设计方法，分别实现了输入饱和多智能体系统的全局及局部状态一致性.抗饱和控制不仅解决了饱和多智能体系统的状态一致性问题，也被用来实现其输出一致性.Lv等[98]研究了输入饱和异构多智能体系统的领导-跟随输出一致性问题，通过引入跟踪误差观测器来生成抗饱和补偿器，实现了输入约束下的全局输出一致性.Wang等[99]将马尔可夫随机切换拓扑结构下的饱和异构多智能体系统作为研究对象，提出一种基于双观测器的分布式动态抗饱和控制方案，解决了由异构智能体交互、输入约束以及非固定拓扑结构等形成的输出一致性难题.

4 总结与展望

本文简述了抗饱和控制的发展历史和基本框架，着重从补偿器结构和激发机制两个方面梳理并总结了抗饱和控制的研究成果.尽管抗饱和控制已经取得一系列重要成果，但其发展也面临着瓶颈；随着控制领域新理念新技术的发展，抗饱和控制也会迎来新的发展机遇.下面我们简述未来抗饱和控制待解决的几个问题.

1) 抗饱和控制的基本框架固定，尤其是基于模型恢复的抗饱和补偿器结构单一，设计自由度较低，如何改进基本框架获取更优的闭环性能是值得关注的；

2) 现有激发机制几乎完全依赖于(虚拟)执行器的饱和状况.实际上，执行器的饱和状况和闭环系统性能之间的联系尚不明朗，也就是说目前抗饱和控制的激发机制与系统性能间的匹配度不高，因此需要开发能够真实反映系统性能的激发机制；

3) 目前抗饱和补偿器设计严重依赖于系统模型参数，针对模型信息未知条件下的研究寥寥无几.因此，利用输入输出数据和学习的方法来设计抗饱和补偿器也是一个可以考虑的途径;

4) 对于饱和多智能体系统，输入饱和约束在不同拓扑结构下对系统性能的关联关系尚未明确，因此拓扑结构对抗饱和补偿器设计及性能的影响有待进一步研究.