基于EMD-EEMD-LSTM的大坝变形预测模型
董 泳,刘肖峰,李云波,贾玉豪
(1.南京市水利规划设计院股份有限公司,江苏 南京 210022;2.河海大学水利水电学院,江苏 南京 210024;3.上海勘测设计研究院有限公司,上海 200335)
0 引 言
大坝作为一种重要的基础设施,在社会、经济发展过程中发挥着重要作用,一旦发生事故,将对下游人民的生命财产造成巨大损失[1]。因此,对大坝行为趋势的分析和预估是至关重要的。变形作为大坝结构性态最直观的指标,选取高效的分析模型对其进行建模、分析,是大坝安全评价系统的重要课题之一[2]。
传统的大坝变形分析方法主要分为3大类——确定性模型、统计模型以及混合模型。这3种模型的缺点主要是建模难、精度不能满足要求等。为此一些学者将机器学习(ML)相关算法引入大坝变形分析领域,如人工神经网络、支持向量机、极限学习机等方法[3-5]。以往ML方法主要针对影响大坝变形的环境因素(如水压、温度和时效等)进行多变量建模,从而构建变形预测模型。然而实际工程中,大坝变形监测数据的波动性往往较强,模型的输入变量不能很好地捕捉变形的变化趋势,造成了模型预测精度不足。如何降低原始变形数据的波动性,是从本质上提高变形预测精度的关键。因此本文引入了Huang等[6]提出的经验模态分解(EMD),旨在将原始变形序列分为若干稳定的分量,进而深入挖掘大坝变形的内在规律。与VMD、小波变换等传统信号分解方法相比,EMD具有不受分解层数以及小波基选择影响的优势,已经在大坝安全监控系统的构建中得到了广泛的应用[7-9]。然而,由于大坝变形的复杂非线性,经过EMD分解得到的高频分量依旧给模型的预测带来一定难度。
为了解决高频分量非线性强、预测精度低等问题,本文提出基于EEMD[10]对其进行再次分解,从而降低高频分量的非线性,最大程度上降低高频分量对整体变形预测精度的影响。经过2次分解得到的一系列变形分量代表变形不同尺度下的变化规律。对于某个分量,其可能受某一环境影响因子的影响或多因素耦合影响。为了解决模型输入变量难以确定的问题,本文提出了使用LSTM[11]对各分量进行建模,考虑各个时间序列的时序相关性。通过查阅文献可知,LSTM的预测性能优于传统ML方法。LSTM独特的“门”结构能够针对时间序列的非线性进行建模分析,通过滑窗的滑动实现预测结果的输出。对各分量分别构建LSTM模型,将得到的预测结果进行叠加,得到最终的变形预测结果。
1 研究方法
1.1 EMD
经验模态分解(EMD)是一种对非线性非平稳信号进行平滑处理的方法。通过EMD分解可以将复杂的原始信号分解为一系列光滑的分量d。为了使得到的时间序列的分解结果有意义,d有2个约束条件:①数据序列的极值点个数与过零点个数之差≤1;②上、下包络线在任意时刻的均值为0。EMD的主要表达式为
(1)
式中,di(t)和r(t)分别为第i个分量以及残差序列;x(t)表示为原始序列,本文中表示大坝原始变形序列。
1.2 EEMD
变形时间序列经EMD分解,将得到一组具有不同频率的分量。其中变形信息的不确定性主要包含在高频分量中,且变形规律难以捕捉,这将造成高频分量的预测结果误差较大。本文针对高频分量提出了二次分解法,旨在分离出高频分量中的有效变形信息,削弱波动性对预测模型输出结果的负面影响,以提高变形预测精度。考虑到高频分量的复杂非线性,为了更有效提取高频分量中的变形信息,本文提出使用EEMD算法对其进行再次分解。
EEMD方法将白噪声加入原始信号[12],然后使用EMD方法对这些新获得的序列进行处理,解决了EMD存在的模态混淆缺陷。EEMD原理为
(1)步骤1。将白噪声加入原始序列x(t),生成新的时间序列y(t)。
(2)步骤2。利用EMD方法对新生成的时间序列进行分解,得到新的di(t)和r(t);。
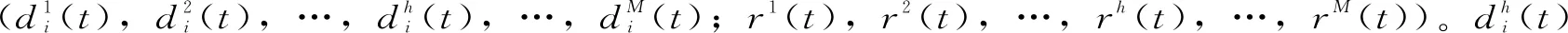
(2)
(3)
1.3 LSTM
LSTM神经网络是一种特殊的递归神经网络,具有学习长期依赖关系的能力。与简单的RNN不同,LSTM神经网络有内置的机制(输入门it、遗忘门ft和输出门ot)来控制信息在整个过程中是如何被记忆或者丢弃的,克服了RNN固有的梯度消失问题。LSTM神经网络的体系结构如图1所示,并由下列公式进行定义。
(4)
(5)
(6)
(7)
ht=ottanh(ct)
(8)
(9)
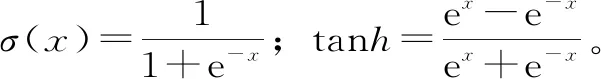
2 模型构建
本文通过EMD分解原始变形序列得到一组包含不同频率的分量(d1,d2,…,dN,r);对于其中的高频分量di,通过EEMD算法进行分解得到一组趋于稳定的分量(D1,D2,…,DP,R);所有分量集合包含了原始变形序列的全部变形信息,选取LSTM作为各分量的时序预测模型,建模并预测得到各分量的预测结果后,将所有预测结果叠加得到最终的输出,从而构建了基于EMD-EEMD-LSTM的大坝变形预测模型,具体流程如图2所示。
3 实例验证
3.1 工程简介和数据采集
以某碾压混凝土拱坝为例,具体说明EMD-EEMD-LSTM模型在大坝变形预测中的优越性。拱坝坝轴线与河道斜交,左右两岸地形不对称。建基面高程130.0 m,坝顶高程234.6 m,最大坝高104.6 m。坝体共分为12个坝段,大坝变形由布置于坝中的垂线系统监测得到。本文选取第4坝段ZC2测点2015年1月1日~2017年8月31日期间的径向变形数据作为分析对象,变形观测数据每日读取一次。在数据分析之前,对其中包含的异常值和缺失值进行预处理。将缺失值进行剔除,并采用线性差值法处理异常值,最终可得966个变形读数,变形曲线见图3。同时将时段划分为训练组、验证组和预测组,其中2015年1月1日~2017年7月2日时段内的数据为训练组,2017年7月3日~2017年8月1日时段内的数据为验证组,2017年8月2日~2017年8月31日时段内的数据为预测组。训练组用以训练LSTM模型,验证组用以检验训练模型的有效性,预测组用以预测评估未来时段内的大坝变形发展趋势。
3.2 EMD、EEMD分解结果
利用EMD算法对原始变形序列进行分解,分解结果见图4。由图4可知,EMD能够将原始序列分解为不同频率的变形信号组合。其中d3、d4为中频信号,d5、d6以及r为低频信号,上述信号通过LSTM建模预测,将得到预期的预测结果。而d1、d2两个高频变形信号表现出明显的波动性,这将给变形预测带来一定的难度,为此本文对信号d1+d2进行再次分解,以深入挖掘高频信号中蕴含的变形信息,基于EEMD的高频分解结果见图5。
由图5可知,经过EEMD分解,高频分量可以被分为11个分量。通过中低频分量可以看出,第1次分解得到的高频分量中依旧包含有用的变形信息,虽然该部分变形信息占比较低,然而忽略此部分将使得预测结果缺乏可靠性,且对预测结果的精度造成一定的负面影响。针对EEMD分解得到的11个变量,由于此部分变形幅度不大,因此采用组合建模方法,即将它们分为高、中、低频3组进行组合预测。其中,D1、D2为高频组合,D3、D4、D5为中频组合,剩余分量为低频组合。
3.3 变形预测结果及对比分析
针对分量d3~d6、r以及二次分解后的3种频率组合分别建立LSTM模型,为对比基于EEMD的高频分解的有效性,考察EEMD分解前后预测结果的精度差异,同时选取了单一多变量BP模型以及LSTM模型作为对比模型,各个模型的预测结果见图6。
由图6可知,各模型预测结果变化曲线差异较大。其中,BP模型对应的变化曲线与实测值的误差最大,说明单一的多变量模型并不能很好地捕捉变形的非线性;LSTM模型的预测结果更接近真实值,然而仍旧无法精确捕捉变形的波动性。相比之下,通过信号分解技术分解后的变形预测结果明显优于单一模型。
图7为各模型预测结果残差图。由图7可知,BP模型的预测残差变化幅度明显高于其中模型,LSTM次之;而EMD-LSTM和EMD-EEMD-LSTM模型对应的残差与x轴形成的误差面积明显小于单一模型。为了进一步对比高频分量分解前后预测结果的精确度,说明挖掘高频分量的必要性,选取RMSE、MAE以及预测结果箱线图作为模型预测性能评价指标,对不同模型的预测结果进行量化评价,各模型的评价指标如图8所示。
由图8可知,分析各模型的预测性能,其中BP和LSTM模型的评价指标明显低于经过2个结合信号分解的模型。对于EMD-LSTM和EMD-EEMD-LSTM模型,可知后者的RMSE和MAE取值均低于前者,验证了讨论高频分量中有效变形信息的重要性。由箱线图(图8a)可以看出,EMD-EEMD-LSTM对应的箱线图与实测值代表的箱线图各项指标最为接近,说明对于大坝这种重要的基础设施来说,变形高频分量中的变形信息不可忽视。
4 结 论
本文构建了一种基于EMD-EEMD-LSTM模型的大坝变形预测分析方法,该方法具有较高的大坝变形预测精度。其中,EMD模型能够有效降低原始序列的波动性;基于EEMD对高频分量进行再次分解,能够进一步降低非线性对变形预测结果的负面影响,深入挖掘变形高频分量中蕴含的变形信息,提升预测性能;选取LSTM作为各分量变形预测器,对每个分量进行建模,考虑变形时序依赖性,提高了模型的预测精度。

